3. Pendule de Foucault#
Marc BUFFAT, dpt mécanique, Université Lyon 1

3.1. Objectif:#
Modélisation du mouvement 3D du pendule de Foucault
mise en équation en utilisant du calcul formel pour faciliter les calculs analytiques (changement de repère, projection, composition des mouvements,..)
résolution numérique des équations pour obtenir la solution
ATTENTION ces outils ne sont pas une boite noir pour résoudre automatiquement les problèmes. Il faut comprendre la démarche pour pouvoir les utiliser à bon escient.
Vous trouverez sur le lien ci-dessous une présentation détaillée de la modélisation du pendule de Foucault
-Présentation détaillée du pendule de Foucault
%matplotlib inline
# bibliothéque numérique
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from IPython.core.display import HTML
from validation.validation import info_etudiant, bib_validation
from validation.valide_markdown import test_markdown, test_code
from IPython.display import display,Image
bib_validation('cours','MGC2028L')
import Pendule3D
# bibliothéque de calcul symbolique
import sympy as sp
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, Particle
3.2. Modélisation du pendule de Foucault#
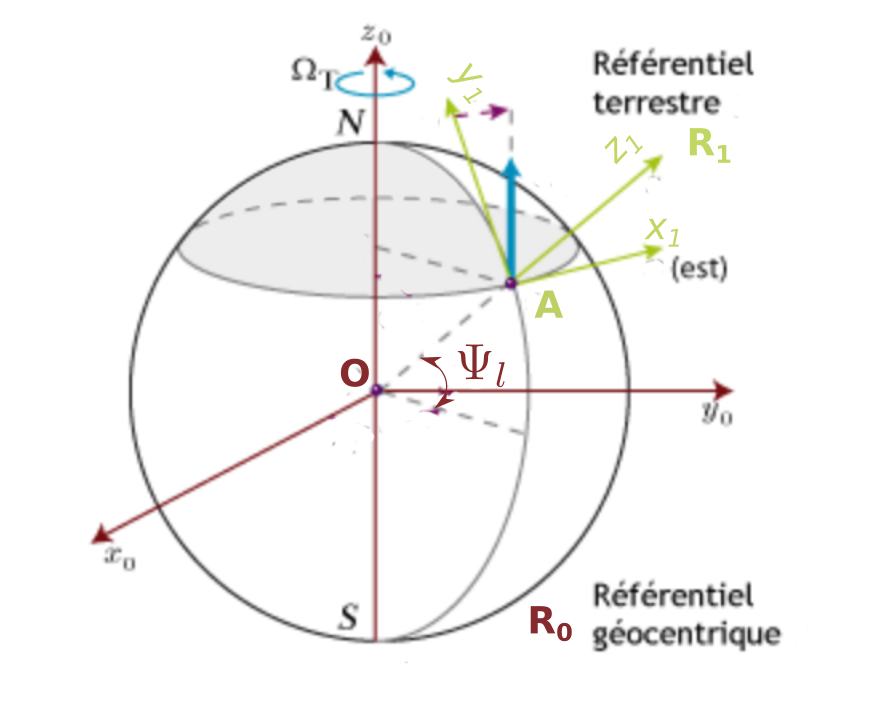
3.2.1. paramètres et repères du problème#
Paramêtres:
R rayon terre
\(\Psi_l\): angle de lattitude (49 degré Paris, 46 degré Lyon)
\(\Omega\): rotation de la terre
Référentiels et points
\(R_0\) référentiel Galiléen (rotation autour de \(R_0z\)
\(R_1\) référentiel du laboratoire (\(R_1z\) vertical, \(R_1x\) orienté WE, \(R_1y\) orienté SN
\(O\) centre terre
\(A\) point du laboratoire (Pentheon à Paris)
# parametres du problème
l, m, R, g, t = sp.symbols('l m R g t')
# rotation de la terre et lattitude
Omega, Psil = sp.symbols('Omega Psi_l')
# degrés de liberté du pendule
theta, phi = dynamicsymbols('theta phi')
# referentiel fixe
O = Point('O')
R0 = ReferenceFrame("R_0")
# repere lié a la terre
Rt = ReferenceFrame("R_t")
Rt.orient(R0,'Axis',[Omega*t + sp.pi/2, R0.z])
# repere laboratoire R1 et point A
R1 = ReferenceFrame("R_1")
R1.orient(Rt,'Axis',[sp.pi/2-Psil, Rt.x])
A = Point('A')
A.set_pos(O,R*R1.z)
3.2.2. application#
Calcul de la position et de la vitesse de A dans R0 en utilisant la composition des vitesses:
méthode
v1pt_theory()expression de la vitesse dans R0 et R1
### BEGIN SOLUTION
display("A=",A.pos_from(O).express(R0),A.pos_from(O).express(R1))
# Vitesse
O.set_vel(R0,0)
A.set_vel(R1,0)
A.v1pt_theory(O,R0,R1)
display("VA=",A.vel(R0).express(R0),A.vel(R0).express(R1))
### END SOLUTION
'A='
'VA='
3.2.3. Etude du pendule dans le laboratoire#
parametres
l longueur pendule, m masse
ddl
\(\theta(t)\) (angle oscillation) et \(\phi(t)\) (précession)
forces
tension \(T\) dans le cable (suivant \(R_3z\))
gravité \(g\) suivant \(R_1z\)

réferentiels
\(R_1\) referentiel du laboratoire (\(R_1z\) vertical)
\(R_2\) rotation de \(\phi\) autour de \(R_1z\)
\(R_3\) rotation de \(\theta\) autour de \(R_2y\) lié au pendule
B point fixation du pendule
P position du pendule
# pendule: vertical R1.z , plan oscillation (R1.x,R1.y)
B = Point('B')
B.set_pos(A,l*R1.z)
R2 = ReferenceFrame("R_2")
R2.orient(R1,'Axis',[phi, R1.z])
R3 = ReferenceFrame("R_3")
R3.orient(R2,'Axis',[-theta, R2.y])
P = Point('P')
P.set_pos(B,-l*R3.z)
3.2.4. application#
Calcul de la position et de la vitesse de P dans R1 en utilisant la composition des vitesses:
méthode
v1pt_theory()expression dans R1,R3
### BEGIN SOLUTION
display("P=",P.pos_from(A),P.pos_from(A).express(R1))
# Vitesse
B.set_vel(R1,0)
B.v1pt_theory(O,R0,R1)
P.set_vel(R3,0)
P.v1pt_theory(B,R1,R3)
display("VP=",P.vel(R1),P.vel(R1).express(R1))
### END SOLUTION
'P='
'VP='
Pe = Particle('Pendule',P,m)
### BEGIN SOLUTION
QP = Pe.linear_momentum(R1)
display("Quantité de mvt de P=",QP)
AP = QP.diff(t,R1).simplify()
display("Variation de quantité de mvt dP/dt=",AP)
### END SOLUTION
'Quantité de mvt de P='
'Variation de quantité de mvt dP/dt='
# bilan des forces: Tension force de tension de module Te et Poids=m*g poids
Te = sp.symbols('T_e')
Poids = None
Tension = None
FT = None
### BEGIN SOLUTION
Poids = - m*g*R1.z
Tension = Te*R3.z
FT = Poids + Tension
FT.express(R3)
### END SOLUTION
3.2.5. Simplification pour un pett pendule#
En appliquant le PFD dans \(R1\), ce qui revient à négliger la rotation de la terre on obtiens les équations du mouvement d’un pendule sphérique en 3D:
voir l” ANNEXE 1 pour la mise en équation
et l”ANNEXE 2 pour la résolution.
# equations dans le cas du pendule sphérique: mvt 3D du pendule
EQS = AP - FT
display("PFD ",EQS,"=0")
'PFD '
'=0'
3.3. Prise en compte de la rotation de la terre#
On considère maintenant la rotation de la terre
le référentiel du laboratoire \(R_1\) n’est plus galiléen et est en rotation avec la terre
le point P est mobile dans \(R_1\), donc sa vitesse / \(R_0\) s’écrit:
de même l’accélération de P / \(R_0\) s’écrit
Dans notre cas la vitesse de rotation de la terre est constante \(\dot{\Omega} = 0\) et on ne conserve que les termes d’ordre 1 en \(\Omega\)
3.3.1. Ordre de grandeur#
calcul de la vitesse et accélération de B / à R0
calcul de la vitesse et accélartion de P / à R1
composition des vitesses et accélération
terme prépondérant: Coriolis
# vitesse de rotation
display("W R1/R0=",R1.ang_vel_in(R0).express(R1))
# vitesse et accélération de B dans R0
### BEGIN SOLUTION
display("V(B) = ",B.vel(R0).express(R1))
# acceleration de B
display("Accel(B) = ",B.acc(R0).express(R1))
### END SOLUTION
'W R1/R0='
'V(B) = '
'Accel(B) = '
# vitesse et accélération de P / R1
VP = P.vel(R1)
display("V(P)/R1=",VP)
AP = P.acc(R1)
display("Accel(P)/R1=",AP)
# vitesse et accélération de P / R0
### BEGIN SOLUTION
display("V(P)/R0=",P.v1pt_theory(B,R0,R1).express(R3).simplify())
# calcul acceleration de P dans R0
display("Accel(P)/R0=",P.a1pt_theory(B,R0,R1).simplify())
display("Accel(P)/R0=",P.a1pt_theory(B,R0,R1).express(R3).simplify())
### END SOLUTION
'V(P)/R1='
'Accel(P)/R1='
'V(P)/R0='
'Accel(P)/R0='
'Accel(P)/R0='
# calcul de l'accélération de Coriolis dans AC
### BEGIN SOLUTION
AC = 2*R1.ang_vel_in(R0).cross(VP).express(R3).simplify()
display("Accel(Coriolis)=",AC)
### END SOLUTION
'Accel(Coriolis)='
3.3.2. PFD avec la force de Coriolis#
On se place dans le référentiel du laboratoire R1, et l’accélération de Coriolis \(\gamma_c\)
apparaît une force de Coriolis \(-m \vec{\gamma_c}\) supplémentaire agissant sur le pendule:
avec $\(\sum \vec{forces} = -mg \vec{z1} + Te \vec{z3} - m \vec{\gamma_c} \)$
calculer le bilan des forces dans FT
en déduire les équations du mouvement dans EQS (sous la forme EQS=0)
FT = 0
EQS = 0
### BEGIN SOLUTION
Poids = - m*g*R1.z
Tension = Te*R3.z
Fc = -m*AC
FT = Poids + Tension + Fc
display("FT=",FT.express(R3))
EQS = m*AP - FT
display("EQS=",EQS)
### END SOLUTION
'FT='
'EQS='
3.3.3. Equations du mouvements#
On obtiens les 2 équations du mouvement par projection suivant R3.x et R3.y (perpendiculaire à la tension), en divisant par \(ml\) et en introduisant \(\omega0=\sqrt{\frac{g}{l}}\)
Mettre le résultat dans les variables eq1c et eq2c
omega0 = sp.symbols('omega_0')
### BEGIN SOLUTION
#display(EQS.dot(R3.x))
eq1c = (EQS.dot(R3.x).subs(g,omega0**2*l)/(l*m)).expand()
display("eq1c:",sp.Eq(eq1c,0))
#display(EQS.dot(R3.y))
eq2c = (EQS.dot(R3.y)/(l*m)).expand()
eq2c = (eq2c).expand()
display("eq2c:",sp.Eq(eq2c,0))
### END SOLUTION
'eq1c:'
'eq2c:'
3.3.4. Analyse du système d’équation#
Pour interpréter les mouvements en mécanique, on cherche des quantités qui se conservent et qui conduisent à des intégrales premières du mouvement. Ces intégrales résultent de l’interprétation des principes fondamentaux de la dynamique:
théorème du moment cinétique: dans un référentiel galiléen, la variation du moment cinétique par rapport à un point fixe O est égale à la somme des moments des forces en O
conservation du moment cinétique: si le moment des forces est nulle dans une direction fixe, alors il y conservation de la composante du moment cinétique dans cette direction.
théorème de l’énergie: dans un référentiel galiléen, la puissance des forces d’accélération est égale à la variation de l’energie cinétique.
conservation de l’energie: si les forces qui travaillent sont conservatives, i.e. découlent d’un potentiel (p.e. la gravité), alors il y a conservation de l’énergie totale du système
3.3.5. Analyse#
Retrouve-t-on ces propriétés de conservation (comme dans le cas du pendule sphérique) ?
Comment peut on vérifier ?
calcul du moment en B des Fext
calcul de la puissance des Fext
### BEGIN SOLUTION
# moment en B des forces : projection suivant R1.z
mt = P.pos_from(B).cross(FT).dot(R1.z)
display("Mt /R1.z = ",mt)
# puissance des forces extérieures (oui c'est la gravité)
display("Pfext=",FT.dot(VP).simplify())
### END SOLUTION
'Mt /R1.z = '
'Pfext='
3.4. Résolution numérique#
Les 2 EDO du mouvement dans eq1c et eq2c s’écrivent sous la forme:
\(\ddot{\theta} = f_{1c}(\theta,\phi)\)
\(\ddot{\phi} \sin\theta = f_{2,c}(\theta,\phi)\)
Or on s’interesse à la solution pour des petits angles \(\theta\). L’équation 2 sur \(\ddot{\phi}\) dégénére à cause du terme en \(\sin\theta\) qui tends vers zéro.
On va donc simplifier la seconde équation en négligeant les termes en \(\sin\theta\) et en divisant par \(2\dot{\theta}\cos\theta\)
# 1ere equation
display("eq1c=",sp.Eq(eq1c,0))
# 2nde equation
display("eq2c=",sp.Eq(eq2c,0))
### BEGIN SOLUTION
f1c = theta.diff(t,2) - eq1c
display(sp.Eq(theta.diff(t,2),f1c))
# simplification equation
eq3c = (eq2c.subs(sp.sin(theta),0)/(2*sp.cos(theta)*theta.diff(t))).expand()
f3c = phi.diff(t)-eq3c
display("eq3c=",sp.Eq(phi.diff(t),f3c))
### END SOLUTION
'eq1c='
'eq2c='
'eq3c='
3.4.1. système d’équations simplifiées#
La nouvelle équation impose donc : $\(\dot{\phi} = - \Omega \sin\Psi_l\)\( c.a.d. une vitesse de précession \)\phi$ constante dans le sens horaire dans l’hémisphère Nord et anti-horaire dans l’hémisphère Sud.
Le système d’équation à résoudre s’écrit, en remplaçant \(\dot{\phi}\) dans la première équation:
On définit les valeurs numériques pour ensuite convertir le second membre f1c en fonction python F1c
# parametres du Pendule Foucault Pantheon
# ========================================
L0 = 67.
OMEGA0 = np.sqrt(9.81/L0)
# lattitude en degre
Lat = 48.5
# periode rotation terre 23h56
OMEGA = 2*np.pi/(23*3600+56*60)
print("Omega0={:.2e} Omega={:.2e} ".format(OMEGA0,OMEGA))
Omega0=3.83e-01 Omega=7.29e-05
# valeurs numériques des parametres
valnums = [(omega0,OMEGA0),(Omega,OMEGA), (Psil,np.deg2rad(Lat))]
display(valnums)
# equations
display("eq1c=",sp.Eq(theta.diff(t,2),f1c))
display("eq3c=",sp.Eq(phi.diff(t),f3c))
# convertion smb en fonction python
F1c = sp.lambdify([theta,theta.diff(t),phi],f1c.subs(phi.diff(t),f3c).subs(valnums),'numpy')
F3c = float(f3c.subs(valnums))
'eq1c='
'eq3c='
3.4.2. Mise sous forme d’équation du 1er ordre#
Le système d’équation à résoudre est un système du second ordre
que l’on va transformer en un système du premier ordre en prenant comme variable d’etat $\( Y = [\theta, \dot{\theta}, \phi ]\)$
Le système à résoudre s’écrit alors :
On définit une fonction second membre penduleFoucault().
def penduleFoucault(etat, temps=0):
'''
calcul le second membre du pendule de Foucault
Arguments
---------
etat : vecteur d'etat [theta, dtheta, phi]
temps: instant t du calcul
Retour
-------
derivs: derivée du vecteur d'etat
'''
global F1c, F3c
### BEGIN SOLUTION
derivs = np.array([etat[1],F1c(etat[0],etat[1],etat[2]), F3c])
return derivs
### END SOLUTION
def iterationRK2(etat, smb, temps, dt):
'''Iteration de RungeKutta 2 pour calculer l'évolution de l'etat sur un pas en temps.
Arguments
---------
etat : vecteur d'etat
smb : fonction qui calcule le second membre de l'EDO fonction de l'etat et du temps
temps: instant du début du calcul
dt : pas en temps
Retour
-------
etat_suiv: movelle valeur du vecteur d'etat après une iteration en temps
'''
etat_milieu = etat + smb(etat,temps) * dt*0.5
etat_suiv = etat + smb(etat_milieu,temps) *dt
return etat_suiv
3.4.3. résolution numérique#
paramètres
Le pendule de Foucault fait 67m de longueur et on le lache à 1m de sa position d’équilibre
choix de la CI
on lache le pendule avec un angle \(\theta_0\) petit dans la direction \(R_1.x\) (lattitude WE) sans vitesse initiale \(\dot{\theta}(0)=0\)
la solution prédit une précession constante de \(\Omega \sin{\Psi_l}\) autour de \(R1_z\) dans le sens horaire
pas en temps et temps de simulation
on choisit une durée d’étude de 4h et 400 pas en temps par période du pendule
iterations de Runge Kutta pour calculer la solutio,
# valeurs des parametres
CI = [1./L0, 0., np.pi/2]
print("CI=",CI)
# temps d'étude
dt = (2*np.pi/OMEGA0)/400
TT = 4*3600
N = int(round(TT/dt))
TT = N*dt
tt = np.linspace(0, TT, N)
print("parametres: N={} dt={:.2e} T={:.2e}".format(N,dt,TT))
CI= [0.014925373134328358, 0.0, 1.5707963267948966]
parametres: N=350784 dt=4.11e-02 T=1.44e+04
# integration numérique: attention peut etre long !!!
sol_num = np.zeros([N,3])
sol_num[0] = CI
### BEGIN SOLUTION
# iteration en temps
for i in range(N-1):
sol_num[i+1] = iterationRK2(sol_num[i], penduleFoucault, tt[i], dt)
# solution
Theta = sol_num[:,0]
dTheta= sol_num[:,1]
Phi = sol_num[:,2]
X = L0*np.sin(Theta)*np.cos(Phi)
Y = L0*np.sin(Theta)*np.sin(Phi)
### END SOLUTION
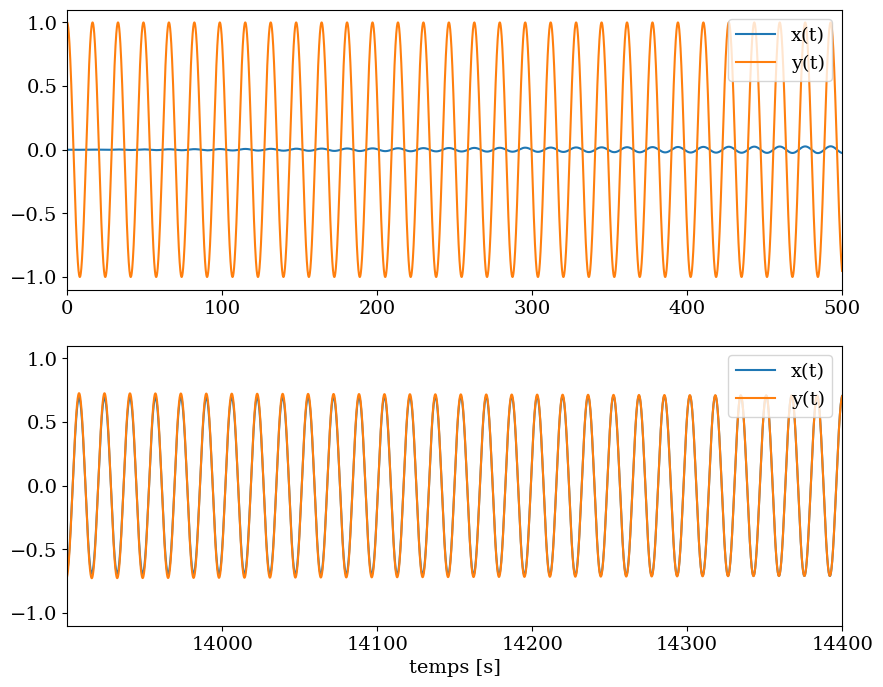
3.4.4. Visualisation de la solution#
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(tt,X,label="x(t)")
plt.plot(tt,Y,label="y(t)")
plt.xlim(0,500)
plt.legend(loc='upper right')
plt.subplot(2,1,2)
plt.plot(tt,X,label="x(t)")
plt.plot(tt,Y,label="y(t)")
plt.xlim(tt[-1]-500,tt[-1])
plt.legend(loc='upper right')
plt.xlabel("temps [s]");
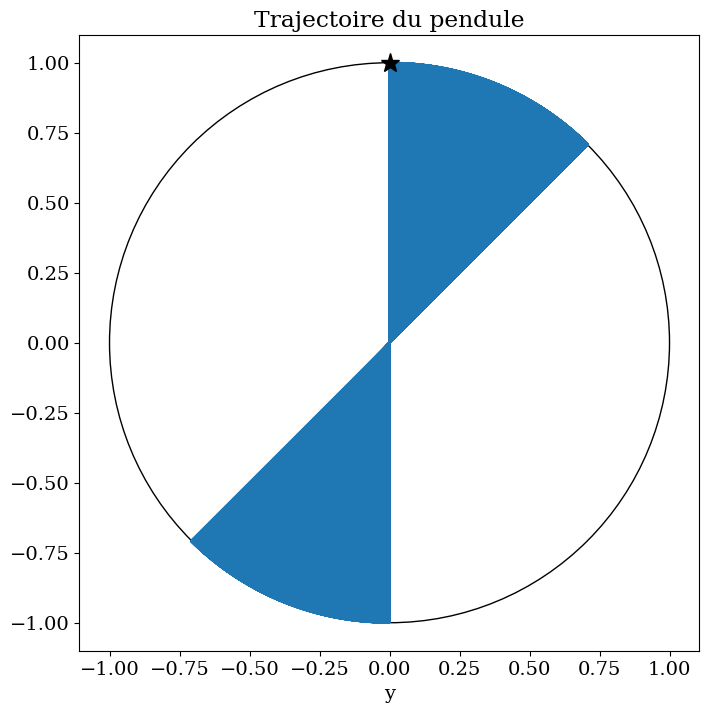
plt.figure(figsize=(8,8))
plt.plot(X,Y)
plt.title("Trajectoire du pendule")
plt.xlabel('x')
plt.xlabel('y')
plt.plot(X[0],Y[0],'*',markersize=14,color='k')
draw_circle = plt.Circle((0., 0.), L0*np.sin(CI[0]),fill=False)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal');
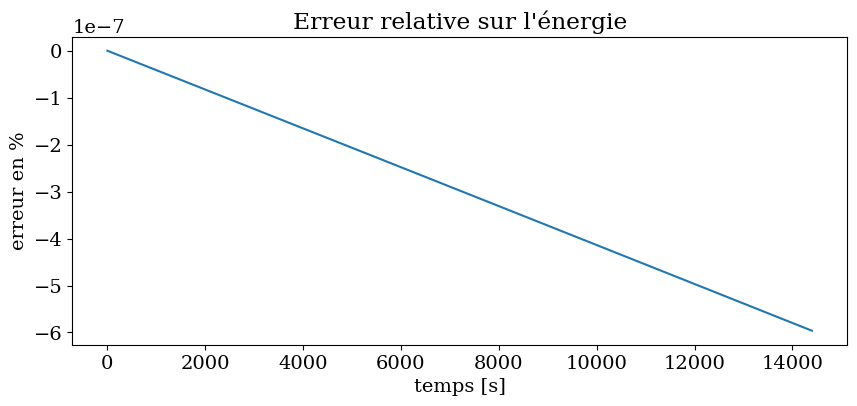
3.4.5. Validation du calcul#
calcul de la période de précession à partir de \(\phi\) calculé
tracé de l’énergie totale
# precession theorique (analyse de Foucault)
OMEGA1 = OMEGA*np.sin(np.deg2rad(Lat))
# verification periode en heures
Phip = (Phi[-1]-Phi[100])/(tt[-1]-tt[100])
print("Periode precession {:.4f} h (theorique {:.4f} h)".format(-2*np.pi/Phip/3600, 2*np.pi/OMEGA1/3600))
Periode precession 31.9557 h (theorique 31.9556 h)
# calcul de l'energie totale
E0 = sp.symbols("E_0")
Ec = Pe.kinetic_energy(R1)
display("Ec=",Ec)
Up = m*g*P.pos_from(B).dot(R1.z)
display("Up=",Up)
eq10 = ((Ec+Up)/(m*l**2)).subs(g,omega0**2*l).simplify()
display("Energie:",sp.Eq(eq10,E0))
'Ec='
'Up='
'Energie:'
eq10a = eq10.subs([(omega0,OMEGA0),(phi.diff(t),-OMEGA1)])
Et = sp.lambdify([theta,theta.diff(t)], eq10a)
ET = Et(Theta,dTheta)
plt.figure(figsize=(10,4))
plt.plot(tt,(ET-ET[0])/ET[0])
plt.xlabel('temps [s]')
plt.ylabel('erreur en %')
plt.title("Erreur relative sur l'énergie");
3.5. Conclusion#
Ecrire vos conclusions
3.5.1. BEGIN SOLUTION#
On observe bien une rotation du plan d’oscillation dans le sens de rotation des aiguilles d’une montre
C’est le contraire dans l’hémisphère nord.
La précision de la méthode de RUnge Kutta 2 sur des temps très longs oblige à prendre des pas en temps très petits
Si on mesure la période de précésion, on peut alors en déduire soit la lattitude \(\Psi_l\) soit la vitesse de rotation de la terre \(\Omega\)
3.5.2. END SOLUTION#
Le pendule que Foucault a installé au Panthéon en 1851 mesurait 67 mètres et portait une masse de 28 kilogrammes. Une fois lancé, ce pendule oscille pendant 6h. La période (aller-retour) étant de 16,5 s, le pendule dévie de 11° par heure. Il faut donc de l’ordre de 32 heures pour une rotation complète du plan d’socillation. Depuis 1995, ce pendule est à nouveau au Panthéon.
3.6. ANNEXE 1: Mouvement du pendule sphérique (sans rotation de la terre)#
On néglige dans un premier temps la rotation de la terre, et on étudie le mouvement du pendule dans le référentiel du laboratoire R1
pendule sphérique 3D
hypothèse: R1 repère Galiléen donc pas d’effet de la rotation de la terre
On définit le pendule comme une masse ponctuelle (Particle) de masse m en P dans la variable Pe.
Dans R1, le PFD stipule que la variation de la quantité de mouvement est égale à la somme des forces appliquées:
On commence par calculer la quantité de mouvement (linear_momentum), que l’on dérive dans R1, et on met le résultat dans la variable AP.
On définit ensuite la somme des forces appliquées dans a variable FT:
la tension \(\vec{T}\) de module Te suivant R3.z: $\(\vec{T}= T_e \;\vec{z_3}\)$
le poids \(- m g \;\vec{z_1}\)
3.6.1. Equations du mouvement dans R1#
en écrivant le PFD dans R1, on obtiens les 3 équations du mouvement en projetant le PFD dans R3 plutôt que R1 (réfléchissez pourquoi ?)
On va simplifier le système d’équation en introduisant la pulsation propre \(\omega_0\) du pendule simple: $\( \omega_0 = \sqrt{\frac{g}{l}} \)\( et on va diviser les équations par \)ml$
# pulsation propre
omega0 = sp.symbols('omega_0')
# equations du mouvement PFD
EQS = None
### BEGIN SOLUTION
EQS = AP - FT
display("PFD 0=",EQS)
EQS=(EQS.express(R3).subs(g,omega0**2*l)/(l*m)).simplify()
display("PFD simplifié 0=",EQS)
### END SOLUTION
'PFD 0='
'PFD simplifié 0='
3.6.2. 3 équations du mouvement#
le système précédent permet obtenir les équations différentielles du mouvement, fonction uniquement des 2 ddl: \(\theta, \phi\), avec
une équation sur \(\ddot{\theta}\) dans eq1,
une équation sur \(\ddot{\phi}\) dans eq2
la dernière équation dans eq3 permet de calculer la tension connaissant \(\theta, \phi\)
Ecrire les 3 équations dans les variables eq1,eq2 et eq3
### BEGIN SOLUTION
eq1 = EQS.dot(R3.x)
display(sp.Eq(eq1,0))
eq2 = EQS.dot(R3.y)
display(sp.Eq(eq2,0))
eq3 = EQS.dot(R3.z)
display(sp.Eq(eq3,0))
### END SOLUTION
3.6.3. Analyse du système d’équation#
Pour interpréter les mouvements en mécanique, on cherche des quantités qui se conservent et qui conduisent à des intégrales premières du mouvement. Ces intégrales résultent de l’interprétation des principes fondamentaux de la dynamique:
théorème du moment cinétique: dans un référentiel galiléen, la variation du moment cinétique par rapport à un point fixe O est égale à la somme des moments des forces en O
conservation du moment cinétique: si le moment des forces est nulle dans une direction fixe, alors il y conservation de la composante du moment cinétique dans cette direction.
théorème de l’énergie: dans un référentiel galiléen, la puissance des forces d’accélération est égale à la variation de l’energie cinétique.
conservation de l’energie: si les forces qui travaillent sont conservatives, i.e. découlent d’un potentiel (p.e. la gravité), alors il y a conservation de l’énergie totale du système
Appliquons ces principes à notre système en remarquant que les seules forces sont la gravité et la tension:
la gravité est une force conservative découlant d’un potenteil \(U_p = m g z_1\) et orienté suivant \(R1_z\)
la tension ne travaille pas, et passe par le point fixe B
On en déduit 2 intégrales premières
conservation de la composante suivant la verticale \( R_1.z\) du moment cinétique en B
conservation de l’énergie totale \(E = E_c + U_p = cste\)
3.6.4. calcul des intégrales premières#
En notant \(\omega_1\) la valeur constante de la composante \(R_1.z\) du moment cinétique en B divisée par \(m l^2\), et \(E_0\) la valeur constante de l’énergie cinétique divisée aussi par \(m l^2\), calculez les 2 intégrales premières en fonction uniquement de \(\theta\) et \(\phi\) et des ces deux constantes dans les variables eq10 (pour l’énergie) et eq21 (pour le moment cinetique)
# calcul mt cinetique / R1.z , energie cinetique et potentielle
mtc_z = None
Ec = None
Up = None
### BEGIN SOLUTION
mtc_z = Pe.angular_momentum(B,R1).dot(R1.z)
display("mt cinetique /R1.z : ",mtc_z)
Ec = Pe.kinetic_energy(R1)
display("Ec=",Ec)
Up = m*g*P.pos_from(B).dot(R1.z)
display("Up=",Up)
### END SOLUTION
'mt cinetique /R1.z : '
'Ec='
'Up='
# calcul des 2 integrales premieres
omega1, E0 = sp.symbols('omega_1 E_0')
eq21 = 0
eq10 = 0
### BEGIN SOLUTION
eq21 = mtc_z/(m*l**2)
eq10 = ((Ec+Up)/(m*l**2)).subs(g,omega0**2*l).simplify()
display(sp.Eq(eq21,omega1))
display(sp.Eq(eq10,E0))
#display(sp.Eq(eq1,0))
display(sp.Eq(eq2,0))
#### END SOLUTION
3.6.5. simplification du système d’équation#
Nous allons remplacer l’équation sur \(\ddot{\phi}\) par la conservation du moment cinétique suivant \(R_1.z\), qui nous donne directement \(\dot{\phi}\) en fonction de \(\theta\), que nous pouvons donc remplacer dans l’équation sur \(\ddot{\theta}\) pour obtenir une équation uniquement en \(\theta\). On écrira les equations sous la forme
\(\ddot{\theta} = \) eq11
\(\dot{\phi} = \) eq22
\( E_0 = \) eq00
L’équation de conservation de l’énergie que l’on simplifie aussi nous servira à valider notre solution numérique.
eq22 = omega1/sp.sin(theta)**2
cdt_phi = [(phi.diff(t),eq22)]
display(cdt_phi)
### BEGIN SOLUTION
eq11 = (theta.diff(t,2)-eq1.subs(cdt_phi)).simplify()
eq00 = eq10.subs(cdt_phi).simplify()
# affiche
print("Equations à résoudre")
display(sp.Eq(theta.diff(t,2),eq11))
display(sp.Eq(phi.diff(t),eq22))
display(sp.Eq(eq00,E0))
### END SOLUTION
Equations à résoudre
3.6.6. analyse du système d’EDO dans 2 cas limites#
3.6.6.1. cas sans précession \(\dot{phi}=0\)#
Si on ne donne pas de mouvement initial de précession, i.e. \(\dot{\phi} = 0\), alors on a \(\omega_1=0\), ce qui donne pour l’équation sur \(\ddot{\theta}\):
qui correspond à l’équation du pendule simple, qui pour de petits angles \(\theta\) $\( \ddot{\theta} = -\omega_0^2 \theta\)\( a une solution harmonique \)\( \theta = \theta_0 \cos{\omega_0 t} \)$
3.6.6.2. cas avec une forte précession initiale#
On suppose maintenant que \(\dot{\phi}\) est grand devant \(\dot{\theta}\approx 0\) que l’on néglige. On a alors \(\theta(t)=cste=\theta_0\). Dans ce cas la vitesse de precéssion est constante et vaut: $\(\dot{\phi} = \frac{\omega_1}{\sin^2{\theta_0}}= cste\)\( le pendule décrit alors des cercles d'axes \)R_1.y\( et de rayon \)l\sin\theta_0$
3.7. ANNEXE 2: étude numérique du mvt 3D du pendule sphérique#
sans prise en compte de l’accélération de Coriolis, nous allons simuler les équations générales du pendule 3d et visualiser les trajectoires en 3D
3.7.1. Intégration numérique#
On considère donc le système d’équations
soit en \(Y = \left[\theta, \dot{\theta}, \psi \right]\)
La valeur de \(\omega_1\) est déterminée par les conditions initiales CI: $\(\theta(0) = \theta_0,\; \dot{\theta}(0) = 0,\; \psi(0) = 0, \; \dot{\psi}(0) = d\psi_0 \)\( ce qui fixe la valeur de \)\omega_1\( \)\( \omega_1 = d\psi_0 \sin{\theta_0}^2 \)$
Algorithme
calcul de la valeur des parametres et des CI pour un pendule de longueur L=1 avec g=9.81
variables CI, Omega0, Omega1 , L et valsnum
calcul du second membre dans une fonction
pendule3Dutilisation de la fonction
iterationRK2boucle d’itération en temps pour calculer la solution
# 1. calcul des CI et des valeurs des parametres valnums
### BEGIN SOLUTION
# CI
CI = [np.pi/5, 0, 0, 2*np.pi/5]
display("CI=",CI)
# parametres numeriques
L = 1.0
Omega0 = np.sqrt(9.81/L)
Omega1 = CI[3] * np.sin(CI[0])**2
valnums = [(l,L),(omega0,Omega0),(omega1,Omega1)]
display("parametres:",valnums)
### END SOLUTION
'CI='
'parametres:'
3.7.1.1. calcul de la fonction second membre#
transformation du second membre de l’équation en \(\ddot{\theta}\) a partir de l’expression analytique en utilisant la fonction sympy lambdify
Ftheta = sp.lambdify([theta,omega0,omega1],expression)
Ecriture de la fonction pendule3D qui calcul le second membre en fonction du vecteur d’etat dans la variable etat et du temps temps
eq12 = omega1**2*sp.cos(theta)/sp.sin(theta)**3 - omega0**2*sp.sin(theta)
display(eq12)
Ftheta = sp.lambdify([theta,omega0,omega1],eq12,'numpy')
def pendule3D(etat, temps=0):
'''
calcul le second membre du pendule sphérique 3D
Arguments
---------
etat : vecteur d'etat [theta, dtheta, phi]
temps: instant t du calcul
Retour
-------
derivs: derivée du vecteur d'etat
'''
global Ftheta,Omega1,Omega0
### BEGIN SOLUTION
derivs = np.array([etat[1], Ftheta(etat[0],Omega0,Omega1), Omega1/np.sin(etat[0])**2])
return derivs
### END SOLUTION
3.7.1.2. iteration de calcul#
On fait une calcul sur 5 périodes du pendule simple avec 500 points de calcul par période.
# integration
### BEGIN SOLUTION
period = 2*np.pi/Omega0
dt = period/500
TT = 5*period
N = round(TT/dt)
tt = np.linspace(0, TT, N)
# solution par la méthode RK2
num_sol = np.zeros([N,3])
#Set intial conditions
num_sol[0,:] = CI[:3]
# calcul de la solution
for i in range(N-1):
num_sol[i+1] = iterationRK2(num_sol[i], pendule3D, tt[i], dt)
### END SOLUTION
3.7.1.3. tracé de la solution#
On trace l’évolution de \(\theta\) et \(\phi\) au cours du temps
attention pour les angles on doit raméner les valeurs entre 0 et \(2\pi\) avec la fonction modulo (pourquoi ?)
On vérifie le calcul en traçant l’énergie totale en fonction du temps en utilisant lambdify
# fonction de calcul de l'energie
Et = sp.lambdify([theta,theta.diff(t),omega0,omega1],eq00)
# calcul de la solution à tracer
Theta = num_sol[:,0]
dTheta= num_sol[:,1]
Phi = np.mod(num_sol[:,2], 2*np.pi)
ET = Et(Theta,dTheta,Omega0,Omega1)
# tracer
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(tt,Theta,label="$\\theta(t)$")
plt.plot(tt,Phi,label="$\\phi(t)$")
plt.xlabel('t [s]')
plt.ylabel("Angles [rd]")
plt.legend()
plt.title("Angles et erreur sur l'énergie totale.\n")
plt.subplot(2,1,2)
plt.plot(tt,(ET-ET[0])/ET[0])
plt.xlabel('t [s]')
plt.ylabel("erreur relative");
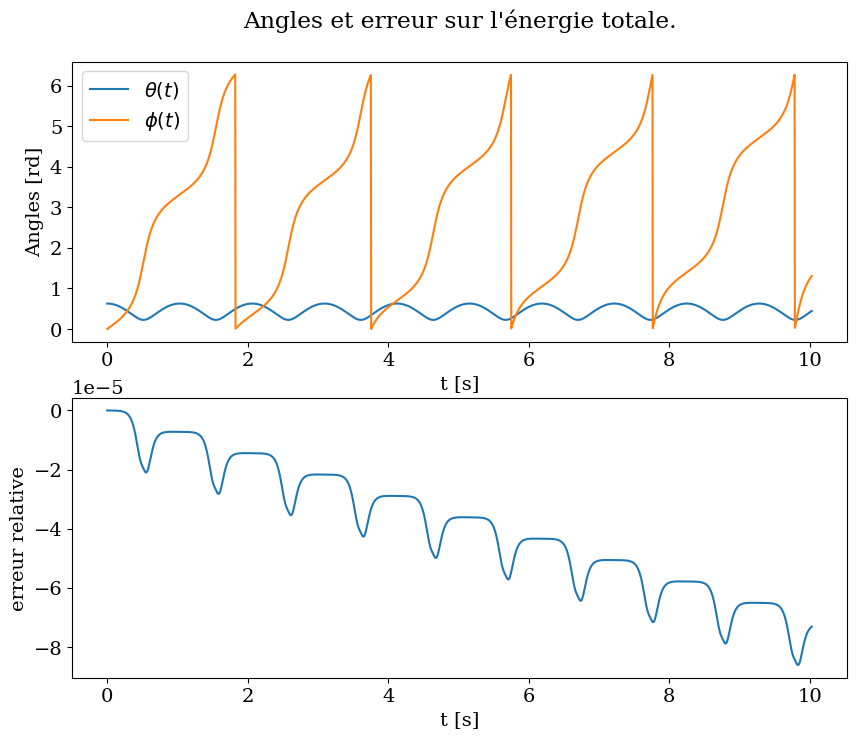
3.7.1.4. analyse du résultat#
écrire ici vos commentaires
3.7.2. Visualisation 3D des trajectoires (petites oscillations)#
pendule3d = Pendule3D.Pendule3D(Ftheta,Omega0,L)
pendule3d.solution(CI,tt[::25])
pendule3d.trace3D()
3.7.3. Visualisation 3D dans le cas avec de grandes amplitudes#
vous pouvez expérimenter en choisisant des CI différentes, p.e.
oscillation pendule simple (precession nulle)
précession rapide (cercle)
pendule3d.solution([np.pi/2,0.,0.,1.5*np.pi/2],tt[::10])
pendule3d.trace3D()
3.8. ANNEXE 3: solution de Foucault (petites oscillations)#
on suppose que le mouvement du pendule reste dans le plan (R1.x,R1.z) et on néglige la variation suivant la verticale R1.y.
on choisit alors comme ddl la position \(x_p(t), y_p(t)\) du pendule dans le plan horizontale en supposant \(z_p(t)=cste\approx 0\)
On est alors en petites oscillations sur \(\theta\) : \(\cos\theta \approx 1\) et \(\sin\theta \approx \theta\), mais par sur \(\phi\) (pourquoi ?)
On va exprimer \(\phi\) en fonction de \(x_p(t), y_p(t)\) en calculant la position de P / a A dans R1 et mettre le résultat dans une liste de substitution cdts
xp, yp = dynamicsymbols('x_p y_p')
AP = xp*R1.x + yp*R1.y
display("AP=",AP)
display("AP=",P.pos_from(A).express(R1))
cdts = [(sp.cos(phi),xp/l/sp.sin(theta)),(sp.sin(phi),yp/l/sp.sin(theta))]
cdts
'AP='
'AP='
3.8.1. Calcul de la projection des forces dans R1#
Il faut calculer la projection des forces dans R1 en fonction des ddl \(x_p(t), y_p(t)\) . On va donc utiliser la liste de substitution cdts
# bilan des forces pour theta petit
Poids = -m*g*R1.z
T = Te*R3.z
FF = (Poids + T).express(R1).subs(cdts).subs(sp.cos(theta),1)
display(FF)
3.8.2. Calcul des accélérations dans R1#
Coriolis dans AC
Accélération relative dans AP
# acceleration de coriolis et acceleration de P dans R1
VP = AP.diff(t,R1)
AC = 2*R1.ang_vel_in(R0).cross(VP)
display("AC=",AC)
AP = VP.diff(t,R1)
display("AP=",AP)
'AC='
'AP='
3.8.3. Application du PFD dans R1#
# PFD
PFD = m*(AC+AP) - FF
display("PFD=",PFD)
'PFD='
simplification
Suivant R1.z , on va négliger le terme en \(\dot{xp}\) devant Te et mg, d’ou la valeur de la tension
$\(Te \approx mg\)$, que l’on va remplacer pour obtenir les 2 équations du mouvement dans eq1l, eq2l
eq1l = (PFD.dot(R1.x).subs(Te,m*g).subs(g,omega0**2*l)/m).expand()
display(sp.Eq(eq1l,0))
eq2l = (PFD.dot(R1.y).subs(Te,m*g).subs(g,omega0**2*l)/m).expand()
display(sp.Eq(eq2l,0))
3.8.4. mise sous forme complexe#
On a un système de 2 équations linéaires couplées, que l’on peut résoudre en passant en variable complexe
les directions Y correspondent à l’axe Sud-Nord et X à l’axe lattitute Est-West
Z = dynamicsymbols('Z')
EQ = Z.diff(t,2) + omega0**2*Z + 2*sp.I*Omega*sp.sin(Psil)*Z.diff(t)
display(sp.Eq(EQ,0))
# vérification
EQ.subs(Z,xp+sp.I*yp).simplify().factor(sp.I)
Cette équation ressemble à l’équation harmonique d’un oscillateur amorti, mais dont l’amortissement est imaginaire, donc n’induit pas une amortissement mais une modulation.
L’équation caractéristique : $\(\lambda^2 + \omega_0^2 +\imath 2 \Omega \sin\Psi_l\)\( admet des racines imaginaires : \)\( \lambda_1, \lambda_2 = -\imath \omega_1 \pm \imath \omega \)$
avec \(\omega^2 = \omega_0^2 + \omega_1^2 \approx \omega_0^2\) car \(\omega_0 \gg \omega_1 = \Omega \sin{\Psi_l} \)
Elle admet donc une solution de la forme
\(A_1 = X_1 + \imath Y_1\) et \(A_2 = X_2 + \imath Y_2\) sont 2 complexes déterminés par les 4 C.I. (position et vitesse suivant les axes x1 et y1)
X1,Y1,X2,Y2 = sp.symbols("X_1 Y_1 X_2 Y2")
Ze = (X1 + sp.I*Y1)* \
(sp.cos(( omega0-omega1)*t) + sp.I*sp.sin(( omega0-omega1)*t)) + \
(X2 + sp.I*Y2)* \
(sp.cos((-omega0-omega1)*t) + sp.I*sp.sin((-omega0-omega1)*t))
Ze = Ze.expand().collect(sp.I)
display("Ze=",Ze)
'Ze='
# conditions initiales
display("Ze(0)=",Ze.subs(t,0).simplify())
display("dZe/dt(0)=",Ze.diff(t).subs(t,0).simplify())
'Ze(0)='
'dZe/dt(0)='
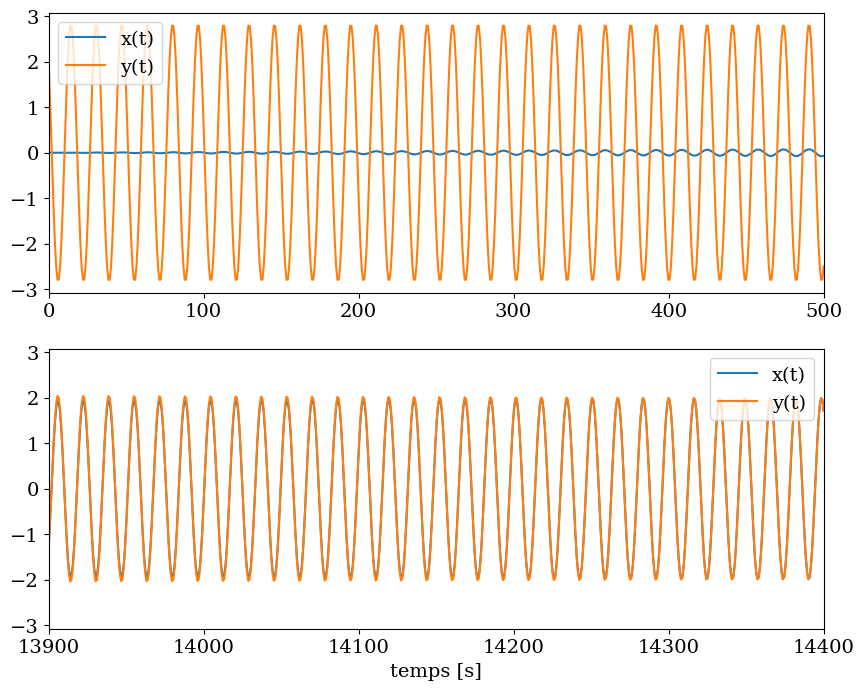
3.8.5. solution particulière#
Le pendule oscille initialement suivant l’axe Sud-Nord: i.e. \(x(0)=0, y(0)=y_0\)
Cette solution peut etre obtenu pour le choix simple suivant: \(X_1 = - X_2 = Y_1 = Y_2 = 1\)
ZZe = Ze.subs([(X1,-1),(X2,1),(Y1,1),(Y2,1)])
display("Ze=",ZZe)
'Ze='
# calcul coordonnees
xe = -sp.sin((omega0-omega1)*t)+sp.sin((omega0+omega1)*t) +\
-sp.cos((omega0-omega1)*t)+sp.cos((omega0+omega1)*t)
ye = -sp.sin((omega0-omega1)*t)-sp.sin((omega0+omega1)*t) +\
sp.cos((omega0-omega1)*t)+sp.cos((omega0+omega1)*t)
display("xe,ye=",xe.simplify(),ye.simplify())
'xe,ye='
# verification erreur en Omega**2
display("Err eq1l=",eq1l.subs([(xp,xe),(yp,ye),(omega1,Omega*sp.sin(Psil))]).doit().simplify())
display("Err eq1l=",eq2l.subs([(xp,xe),(yp,ye),(omega1,Omega*sp.sin(Psil))]).doit().simplify())
'Err eq1l='
'Err eq1l='
# application Pendule Foucault Pantheon
OMEGA0 = np.sqrt(9.81/67.)
# lattitude en degre
Lat = 48.5
# periode rotation terre 23h56
OMEGA = 2*np.pi/(23*3600+56*60)
OMEGA1 = OMEGA*np.sin(np.deg2rad(Lat))
# amplitude des oscillations
A0 = 2*np.sqrt(2)
print("Omega0={:.2e} Omega={:.2e} Omega1={:.2e}".format(OMEGA0,OMEGA,OMEGA1))
# solution
Xe = sp.lambdify([t],xe.subs([(omega0,OMEGA0),(omega1,OMEGA1)]))
Ye = sp.lambdify([t],ye.subs([(omega0,OMEGA0),(omega1,OMEGA1)]))
# periode de precesion du pendule en jours
print("Periode précession {:.2f} jours".format(2*np.pi/(OMEGA1)/3600.))
Omega0=3.83e-01 Omega=7.29e-05 Omega1=5.46e-05
Periode précession 31.96 jours
# temps d'étude
dt = (2*np.pi/OMEGA0)/20
TT = 4*3600
N = round(TT/dt)
tt = np.linspace(0, TT, N)
X = Xe(tt)
Y = Ye(tt)
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(tt,X,label="x(t)")
plt.plot(tt,Y,label="y(t)")
plt.xlim(0,500)
plt.legend()
plt.subplot(2,1,2)
plt.plot(tt,X,label="x(t)")
plt.plot(tt,Y,label="y(t)")
plt.xlim(tt[-1]-500,tt[-1])
plt.legend()
plt.xlabel("temps [s]");
plt.figure(figsize=(8,8))
plt.plot(X,Y)
plt.title("Trajectoire du pendule")
plt.xlabel('x')
plt.xlabel('y')
plt.plot(X[0],Y[0],'*',markersize=14,color='k')
draw_circle = plt.Circle((0., 0.), A0,fill=False)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal');
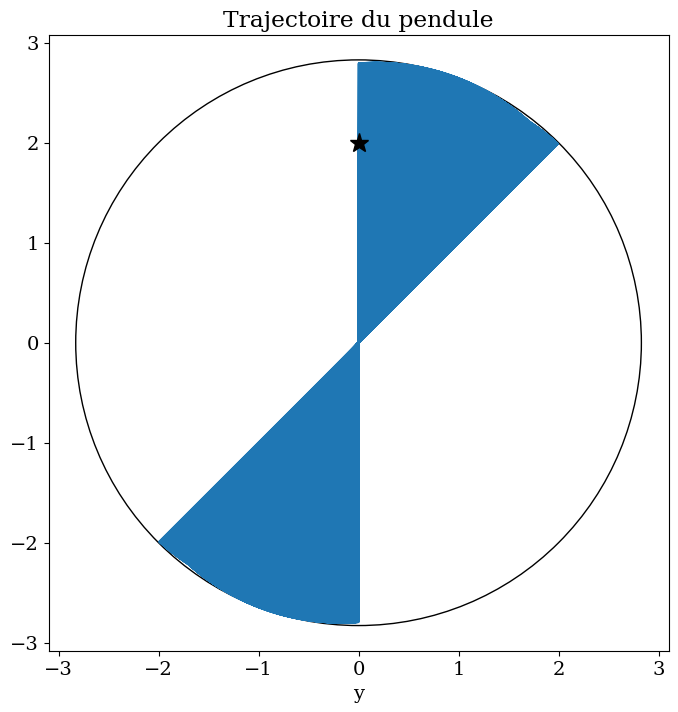
3.9. FIN de la leçon#
# version
from platform import python_version,uname,platform
print("Systeme :",uname())
print("OS :",platform())
print("version python:",python_version())
print("version sympy :",sp.__version__)
print("version numpy :",np.__version__)
Systeme : uname_result(system='Linux', node='p2chpd-visu2', release='5.15.0-160-generic', version='#170-Ubuntu SMP Wed Oct 1 10:06:56 UTC 2025', machine='x86_64')
OS : Linux-5.15.0-160-generic-x86_64-with-glibc2.35
version python: 3.10.12
version sympy : 1.11.1
version numpy : 1.26.4
