Cinématique d’une trottinette

Contenu

7. Cinématique d’une trottinette#

Marc BUFFAT département mécanique, université Lyon 1

 "Life is like riding a bicycle. 
  To keep your balance, you must keep moving.”
  (Albert Einstein)

trottinette_elec.jpg

%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display,Image
from sympy.physics.vector import Vector, init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
#
from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
from validation.validation import info_etudiant
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    printmd("## ERREUR: numéro d'étudiant non spécifié!!!")
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
    #raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_    = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Etudiant {} {}  id={}**".format(NOM,PRENOM,NUMERO_ETUDIANT))

ERREUR: numéro d’étudiant non spécifié!!!

Etudiant Marc BUFFAT id=137764122

7.1. Problème#

Soit le modèle de trottinette ci-dessous

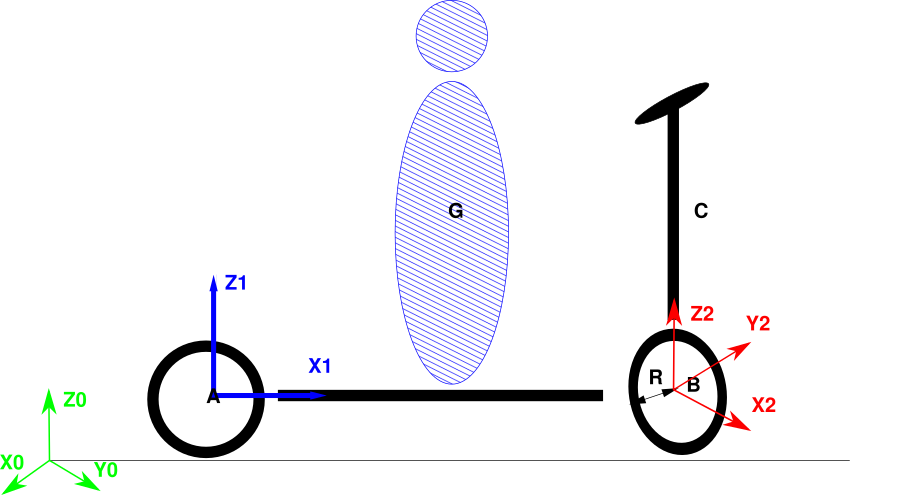
trottinette.png

La trottinette consiste en un cadre AC horizontale de longueur L, une fourche verticale CB pouvant tourné suivant l’axe CB, une roue arrière d’axe A de rayon r et une roue avant d’axe B de même rayon r. Le conducteur de la trottinette a son centre de gravité en G au milieu de AB et distant de h suivant la verticale.

La cinématique de la trottinette est donnée par la position de A et sa vitesse (fournit par le moteur), ainsi que la position des autres éléments par rapport à A et des conditions cinématiques (contacte sans glissement).

On note O un point d’origine et \(R_0\) le repère fixe d’axe vertical \(R_0.z\), La trottinette se déplace sur un plan horizontal (\(R_0.x\),\(R_0.y\)) en conservant un cadre dans le plan vertical. Soit \(R_1\) le repère lié au cadre en A, de position \(x_A,y_A\) et orienté dans le sens de la vitesse en A est en rotation dans le plan horizontal avec un angle \(\psi\) autour de la verticale \(R_0.z\). On note \(L\) la distance entre l’axe des 2 roues \(A\) et \(B\), et on suppose que \(G\) est à égale distance de \(A\) et \(B\) et distant de \(h\) en hauteur. On note \(R_2\) le repère lié à la fourche qui est en rotation d’angle \(\phi\) autour de \(R_1.z\). On note \(R_3\) le repère lié à la roue arrière qui est en rotation d’angle \(\theta_1\) autour de \(R_1.y\), et \(R_4\) le repère lié à la roue avant qui est en rotation d’angle \(\theta_2\) autour de \(R_2.y\).

7.1.1. objectifs#

on se propose de déterminer la cinématique de la trottinette dans le cas général, puis dans le cas d’une trajectoire rectiligne (pour vérification) et enfin dans le cas d’une trajectoire circulaire de rayon \(R\).

Le travail demandé est une validation de l’approche, ainsi qu’une analyse des résultats, puis à la fin une conclusion.

ATTENTION on executera le notebook depuis le début jusqu’à la fin en utilisant le bouton > Exécuter

7.1.2. modélisation#

5 repères:

  • (O,R0) fixe ,

  • (A,R1) lié au cadre avec l’axe \(R1.x\) orienté suivant la direction de la vitesse en A (angle \(\psi\)).

  • (B,R2) lié à la fourche (rotation \(\phi\))

  • (A,R3) lié à la roue arrière (rotation \(\theta_1\))

  • (B,R4) lié à la roue avant (rotation \(\theta_2\))

La position de la trottinette avec ses roues et son conducteur est donc donnée par:

  • la position \(x_a,y_a\) de \(A\) par rapport à O,

  • sa vitesse d’amplitude \(u_a\) d’angle \(\psi\) qui correspond à la rotation du cadre autour de \(R_0.z\),

  • la rotation d’angle \(\phi\) de la fourche par rapport au cadre autour de \(R_1.z\)

  • les rotations d’angles \(\theta_1\) et \(\theta_2\) des roues par rapport à \(R_1.y\) et \(R_2.y\).

Des paramétres: r (rayon roue),h (hauteur de G),L (longueur du cadre),R (rayon de la trajectoire)

7.2. Modèle cinématique#

7.2.1. définition des paramétres#

from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
# parametres du problème
r, L, h, R, t = sp.symbols('r L h R t')
# degrés de liberté
xa, ya  = dynamicsymbols('x_a y_a')
ua = dynamicsymbols('u_a')
psi, phi, theta1, theta2 = dynamicsymbols('psi phi theta_1 theta_2')

# relation cinématique
display(sp.Eq(xa.diff(t),ua*sp.cos(psi)))
display(sp.Eq(ya.diff(t),ua*sp.sin(psi)))
relU = [(xa.diff(t), ua*sp.cos(psi)),(ya.diff(t), ua*sp.sin(psi))]
display(relU)
\[\displaystyle \dot{x}_{a} = u_{a} \cos{\left(\psi \right)}\]
\[\displaystyle \dot{y}_{a} = u_{a} \sin{\left(\psi \right)}\]
\[\displaystyle \left[ \left( \dot{x}_{a}, \ u_{a} \cos{\left(\psi \right)}\right), \ \left( \dot{y}_{a}, \ u_{a} \sin{\left(\psi \right)}\right)\right]\]

7.2.2. définition des repères#

  • 5 repères R0, R1, R2, R3, R4

  • 6 points O, A, B, G, P1, P2

# reperes et points
O = Point('O')
R0 = ReferenceFrame('R_0')
# cadre
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[psi, R0.z])
A = Point('A')
A.set_pos(O,xa*R0.x + ya*R0.y + r*R0.z )
# roue arriere
R3 = ReferenceFrame('R_3')
R3.orient(R1,'Axis',[theta1, R1.y])
# point P1 de la roue arriere
P1 = Point('P1')
P1.set_pos(A,r*R3.z)
# centre de gravité
G = Point('G')
G.set_pos(A, L/2*R1.x + h*R1.z)
# fourche 
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[phi, R1.z])
B = Point('B')
B.set_pos(A, L*R1.x)
# roue avant
R4 = ReferenceFrame('R_4')
R4.orient(R2,'Axis',[theta2, R2.y])
# point P2 de la roue avant
P2 = Point('P2')
P2.set_pos(B,r*R4.z)

7.2.3. Calcul de la position des points dans R0#

dans la cellule suivante, calculer la position de G,A et B dans le repère R0 et mettre le résultat dans les 3 variables OG, OA et OB

# positions dans R0 du cadre
OG = 0
OA = 0
OB = 0
### BEGIN SOLUTION
OG = G.pos_from(O).express(R0).simplify()
OA = A.pos_from(O).express(R0).simplify()
OB = B.pos_from(O).express(R0).simplify()
### END SOLUTION 

display("OA=",OA)
assert(OA == Vector.express(Point.pos_from(A,O),R0).simplify())
display("OB=",OB)
assert(OB == Vector.express(Point.pos_from(B,O),R0).simplify())
display("OG=",OG)
assert(OG == Vector.express(Point.pos_from(G,O),R0).simplify())

'OA='
\[\displaystyle x_{a}\mathbf{\hat{r_0}_x} + y_{a}\mathbf{\hat{r_0}_y} + r\mathbf{\hat{r_0}_z}\]
'OB='
\[\displaystyle (L \cos{\left(\psi \right)} + x_{a})\mathbf{\hat{r_0}_x} + (L \sin{\left(\psi \right)} + y_{a})\mathbf{\hat{r_0}_y} + r\mathbf{\hat{r_0}_z}\]
'OG='
\[\displaystyle (\frac{L \cos{\left(\psi \right)}}{2} + x_{a})\mathbf{\hat{r_0}_x} + (\frac{L \sin{\left(\psi \right)}}{2} + y_{a})\mathbf{\hat{r_0}_y} + (h + r)\mathbf{\hat{r_0}_z}\]

7.2.3.1. position des roues#

dans la cellule suivante, calculer la position du point P1 de la roue arrière par rapport à B et celle du point P2 de la roue avant par rapport à B dans le repère R1 et mettre le résultat dans les 2 variables AP1 et BP2

# position des roues
print("Position des roues P1 et P2:")
AP1 = 0
BP2 = 0
### BEGIN SOLUTION
AP1 = P1.pos_from(A).express(R1).simplify()
BP2 = P2.pos_from(B).express(R1).simplify()
### END SOLUTION

Position des roues P1 et P2:

display("AP1=",AP1)
assert(AP1 == Vector.express(Point.pos_from(P1,A),R1).simplify())
display("BP2=",BP2)
assert(BP2 == Vector.express(Point.pos_from(P2,B),R1).simplify())

'AP1='
\[\displaystyle r \sin{\left(\theta_{1} \right)}\mathbf{\hat{r_1}_x} + r \cos{\left(\theta_{1} \right)}\mathbf{\hat{r_1}_z}\]
'BP2='
\[\displaystyle r \sin{\left(\theta_{2} \right)} \cos{\left(\phi \right)}\mathbf{\hat{r_1}_x} + r \sin{\left(\phi \right)} \sin{\left(\theta_{2} \right)}\mathbf{\hat{r_1}_y} + r \cos{\left(\theta_{2} \right)}\mathbf{\hat{r_1}_z}\]

7.2.4. cinématique#

calcul des vitesses en utilisant la composition de mouvement

# O origine
O.set_vel(R0,0.)
A.set_vel(R0,ua*R1.x)
# vitesse du cadre
A.set_vel(R1,0.)
display("VA=",A.vel(R0))
G.set_vel(R1,0.)
display("VG=",G.v1pt_theory(A,R0,R1))
B.set_vel(R1,0.)
display("VB=",B.v2pt_theory(A,R0,R1))

'VA='
\[\displaystyle u_{a}\mathbf{\hat{r_1}_x}\]
'VG='
\[\displaystyle u_{a}\mathbf{\hat{r_1}_x} + \frac{L \dot{\psi}}{2}\mathbf{\hat{r_1}_y}\]
'VB='
\[\displaystyle u_{a}\mathbf{\hat{r_1}_x} + L \dot{\psi}\mathbf{\hat{r_1}_y}\]
# vitesse des roues
display("VP1=",P1.v2pt_theory(A,R0,R3).express(R1).simplify())
display("VP2=",P2.v2pt_theory(B,R0,R4).express(R2).simplify())

'VP1='
\[\displaystyle (r \cos{\left(\theta_{1} \right)} \dot{\theta}_{1} + u_{a})\mathbf{\hat{r_1}_x} + r \sin{\left(\theta_{1} \right)} \dot{\psi}\mathbf{\hat{r_1}_y} - r \sin{\left(\theta_{1} \right)} \dot{\theta}_{1}\mathbf{\hat{r_1}_z}\]
'VP2='
\[\displaystyle (L \sin{\left(\phi \right)} \dot{\psi} + r \cos{\left(\theta_{2} \right)} \dot{\theta}_{2} + u_{a} \cos{\left(\phi \right)})\mathbf{\hat{r_2}_x} + (L \cos{\left(\phi \right)} \dot{\psi} + r \left(\dot{\phi} + \dot{\psi}\right) \sin{\left(\theta_{2} \right)} - u_{a} \sin{\left(\phi \right)})\mathbf{\hat{r_2}_y} - r \sin{\left(\theta_{2} \right)} \dot{\theta}_{2}\mathbf{\hat{r_2}_z}\]
# projection dans R1
VP1=P1.vel(R0).express(R1).simplify()
display("VP1=",VP1)
VP2=P2.vel(R0).express(R2).simplify()
display("VP2=",VP2)

'VP1='
\[\displaystyle (r \cos{\left(\theta_{1} \right)} \dot{\theta}_{1} + u_{a})\mathbf{\hat{r_1}_x} + r \sin{\left(\theta_{1} \right)} \dot{\psi}\mathbf{\hat{r_1}_y} - r \sin{\left(\theta_{1} \right)} \dot{\theta}_{1}\mathbf{\hat{r_1}_z}\]
'VP2='
\[\displaystyle (L \sin{\left(\phi \right)} \dot{\psi} + r \cos{\left(\theta_{2} \right)} \dot{\theta}_{2} + u_{a} \cos{\left(\phi \right)})\mathbf{\hat{r_2}_x} + (L \cos{\left(\phi \right)} \dot{\psi} + r \left(\dot{\phi} + \dot{\psi}\right) \sin{\left(\theta_{2} \right)} - u_{a} \sin{\left(\phi \right)})\mathbf{\hat{r_2}_y} - r \sin{\left(\theta_{2} \right)} \dot{\theta}_{2}\mathbf{\hat{r_2}_z}\]

7.2.5. analyse des conditions cinématiques de non-glissement#

La condition de roulement sans glissement des 2 roues implique l’annulation de la vitesse des points P1 et P2 lorsqu’ils sont en contacte avec le sol, i.e. pour \(\theta=\pi\). On obtiens donc

  • 3 conditions

  • cela permet de calculer la rotation des 2 roues \(\omega_1,\omega_2\), et l’angle de rotation \(\phi\) de la fourche si on se donne la vitesse \(u_a\) et sa direction \(\psi\)

7.2.5.1. calcul de la vitesse des roues au point de contacte#

Au point de contacte, on a \(\dot{\theta}=\omega\) et \(\theta=\pi\)

# condition de roulement sans glissement roue arriere: VG1=0
omega1 = sp.symbols("omega_1")
display("VP1=",VP1)
VG1=VP1.subs([(theta1.diff(t),omega1),(theta1,sp.pi)])
display("cdt de non glissement: VG1=0",VG1)

'VP1='
\[\displaystyle (r \cos{\left(\theta_{1} \right)} \dot{\theta}_{1} + u_{a})\mathbf{\hat{r_1}_x} + r \sin{\left(\theta_{1} \right)} \dot{\psi}\mathbf{\hat{r_1}_y} - r \sin{\left(\theta_{1} \right)} \dot{\theta}_{1}\mathbf{\hat{r_1}_z}\]
'cdt de non glissement: VG1=0'
\[\displaystyle (- \omega_{1} r + u_{a})\mathbf{\hat{r_1}_x}\]
# condition de roulement sans glissement roue avant: VP2=0
omega2 = sp.symbols("omega_2")
display("VP2=",VP2)
VG2=VP2.subs([(theta2.diff(t),omega2),(theta2,sp.pi)])
display("cdt de non glissement: VG2=0",VG2)

'VP2='
\[\displaystyle (L \sin{\left(\phi \right)} \dot{\psi} + r \cos{\left(\theta_{2} \right)} \dot{\theta}_{2} + u_{a} \cos{\left(\phi \right)})\mathbf{\hat{r_2}_x} + (L \cos{\left(\phi \right)} \dot{\psi} + r \left(\dot{\phi} + \dot{\psi}\right) \sin{\left(\theta_{2} \right)} - u_{a} \sin{\left(\phi \right)})\mathbf{\hat{r_2}_y} - r \sin{\left(\theta_{2} \right)} \dot{\theta}_{2}\mathbf{\hat{r_2}_z}\]
'cdt de non glissement: VG2=0'
\[\displaystyle (L \sin{\left(\phi \right)} \dot{\psi} - \omega_{2} r + u_{a} \cos{\left(\phi \right)})\mathbf{\hat{r_2}_x} + (L \cos{\left(\phi \right)} \dot{\psi} - u_{a} \sin{\left(\phi \right)})\mathbf{\hat{r_2}_y}\]

7.2.5.2. relations de non glissement#

calcul de la rotation des 2 roues \(\omega_1,\omega_2\), et l’angle de rotation \(\phi\) de la fourche en fonction de la vitesse \(u_a\) et sa direction \(\psi=\psi_0\)

# cdts de non glissement roue arriere
cdtsGL1=[(omega1,sp.solve(VG1.dot(R1.x),omega1)[0])]
display("cdt de non glissement roue arriere:",cdtsGL1)
# cdts de non glissement roue avant
phi0=sp.symbols("phi_0")
eq1=VG2.dot(R2.x)
eq2=VG2.dot(R2.y)
eq11=(sp.cos(phi)*eq1-sp.sin(phi)*eq2).simplify()
eq22=(sp.sin(phi)*eq1+sp.cos(phi)*eq2).simplify()

cdtsGL2=[(phi0,sp.solve(eq22.subs([(omega2,sp.solve(eq11,omega2)[0])]),phi)[0]),
         (omega2,sp.solve(eq11,omega2)[0].subs(phi,phi0))]
display("cdt de non glissement roue avant:",cdtsGL2)

'cdt de non glissement roue arriere:'
\[\displaystyle \left[ \left( \omega_{1}, \ \frac{u_{a}}{r}\right)\right]\]
'cdt de non glissement roue avant:'
\[\displaystyle \left[ \left( \phi_{0}, \ 2 \operatorname{atan}{\left(\frac{\sqrt{L^{2} \dot{\psi}^{2} + u_{a}^{2}} - u_{a}}{L \dot{\psi}} \right)}\right), \ \left( \omega_{2}, \ \frac{u_{a}}{r \cos{\left(\phi_{0} \right)}}\right)\right]\]

7.3. Vérification dans le cas d’une trajectoire rectiligne#

Pour une trajectoire rectiligne uniforme, la vitesse est constante en module et direction

  • \(u_a = cste\) fixé

  • \(\dot{\psi} = 0\) donc \(\psi=cste\)

la position de A est fonction de l’angle initial de la vitesse \(\psi(0) = \psi_0\)

\[x_a = u_a \cos(\psi_0) t, y_a = u_a \sin(\psi_0) t\]

les conditions de roulement sans glissement impose l’alignement de la fourche et du cadre:

\[\phi = 0\]
\[\dot{\theta_1} = \omega_1 = \frac{u_a}{r} = \dot{\theta_2} = \omega_2 \]

7.3.1. conditions de roulement sans glissement#

# cdts de roulement sans glissement
cdts = [(psi.diff(t),0),(phi,0)]
display("VG1=0",VG1)
display("VG2=0",VG2.subs(cdts))

'VG1=0'
\[\displaystyle (- \omega_{1} r + u_{a})\mathbf{\hat{r_1}_x}\]
'VG2=0'
\[\displaystyle (- \omega_{2} r + u_{a})\mathbf{\hat{r_2}_x}\]

On a donc forcement $\(\omega_1 = \omega_2 = \frac{u_A}{r}\)$

# conditions cinematiques
cdtsNG=[(theta1,omega1*t),(theta2,omega2*t),
        (omega1,ua/r),(omega2,ua/r),(xa,ua*sp.cos(psi)*t),(ya,ua*sp.sin(psi)*t)]
display("condition rlt sans glissement:",cdtsNG)

'condition rlt sans glissement:'
\[\displaystyle \left[ \left( \theta_{1}, \ \omega_{1} t\right), \ \left( \theta_{2}, \ \omega_{2} t\right), \ \left( \omega_{1}, \ \frac{u_{a}}{r}\right), \ \left( \omega_{2}, \ \frac{u_{a}}{r}\right), \ \left( x_{a}, \ t u_{a} \cos{\left(\psi \right)}\right), \ \left( y_{a}, \ t u_{a} \sin{\left(\psi \right)}\right)\right]\]

7.3.2. calcul de la trajectoire numériquement#

On fixe la valeur de tous les paramêtres pour avoir uniquement des expressions en fonction de t, que l’on peut ensuite calculer numériquement (avec une petite bibliothéque python et une classe Trottinnette)

# valeurs des parametres numériques en USI
valnum=[(L,1.),(r,0.05),(h,1.),(ua,1*0.27778),(psi,np.pi/6),(phi,0)]
display(valnum)
\[\displaystyle \left[ \left( L, \ 1.0\right), \ \left( r, \ 0.05\right), \ \left( h, \ 1.0\right), \ \left( u_{a}, \ 0.27778\right), \ \left( \psi, \ 0.523598775598299\right), \ \left( \phi, \ 0\right)\right]\]

7.3.2.1. vérification#

calculer l’expression numérique fonction de t de la position de A, B, de P1 et de P2 dans R0 et mettre le résultat dans les variables OA, OB, OP1 et OP2 et vérifier que cela correspond bien à la trajectoire attendue

# vérification
OA = 0
OB = 0
OP1 = 0
OP2 = 0
### BEGIN SOLUTION
OA  = A.pos_from(O).express(R0).subs(cdtsNG).subs(valnum)
OB  = B.pos_from(O).express(R0).subs(cdtsNG).subs(valnum)
OP1 = P1.pos_from(O).express(R0).subs(cdtsNG).subs(valnum)
OP2 = P2.pos_from(O).express(R0).subs(cdtsNG).subs(valnum)
### END SOLUTION

display("OA=",OA)
assert(OA == Vector.express(Point.pos_from(A,O),R0).subs(cdtsNG).subs(valnum))
display("OB=",OB)
assert(OB == Vector.express(Point.pos_from(B,O),R0).subs(cdtsNG).subs(valnum))
display("OP1=",OP1)
assert(OP1 == Vector.express(Point.pos_from(P1,O),R0).subs(cdtsNG).subs(valnum))
display("OP2=",OP2)
assert(OP2 == Vector.express(Point.pos_from(P2,O),R0).subs(cdtsNG).subs(valnum))

'OA='
\[\displaystyle 0.240564536663241 t\mathbf{\hat{r_0}_x} + 0.13889 t\mathbf{\hat{r_0}_y} + 0.05\mathbf{\hat{r_0}_z}\]
'OB='
\[\displaystyle (0.240564536663241 t + 0.866025403784439)\mathbf{\hat{r_0}_x} + (0.13889 t + 0.5)\mathbf{\hat{r_0}_y} + 0.05\mathbf{\hat{r_0}_z}\]
'OP1='
\[\displaystyle (0.240564536663241 t + 0.0433012701892219 \sin{\left(5.5556 t \right)})\mathbf{\hat{r_0}_x} + (0.13889 t + 0.025 \sin{\left(5.5556 t \right)})\mathbf{\hat{r_0}_y} + (0.05 \cos{\left(5.5556 t \right)} + 0.05)\mathbf{\hat{r_0}_z}\]
'OP2='
\[\displaystyle (0.240564536663241 t + 0.0433012701892219 \sin{\left(5.5556 t \right)} + 0.866025403784439)\mathbf{\hat{r_0}_x} + (0.13889 t + 0.025 \sin{\left(5.5556 t \right)} + 0.5)\mathbf{\hat{r_0}_y} + (0.05 \cos{\left(5.5556 t \right)} + 0.05)\mathbf{\hat{r_0}_z}\]
# bibliotheque de tracer des trajectoires
from validation.Trottinette import Trottinette
trottinette =  Trottinette([O,A,B,G,P1,P2], [R0,R1], [r,h,L,R], cdts, cdtsNG, valnum)

# calcul sur un temps tmax
tmax = float((2*L/ua).subs(valnum))
print("tmax=",tmax)
trottinette.traj2D([A,G,B],t,tmax)

tmax= 7.199942400460795
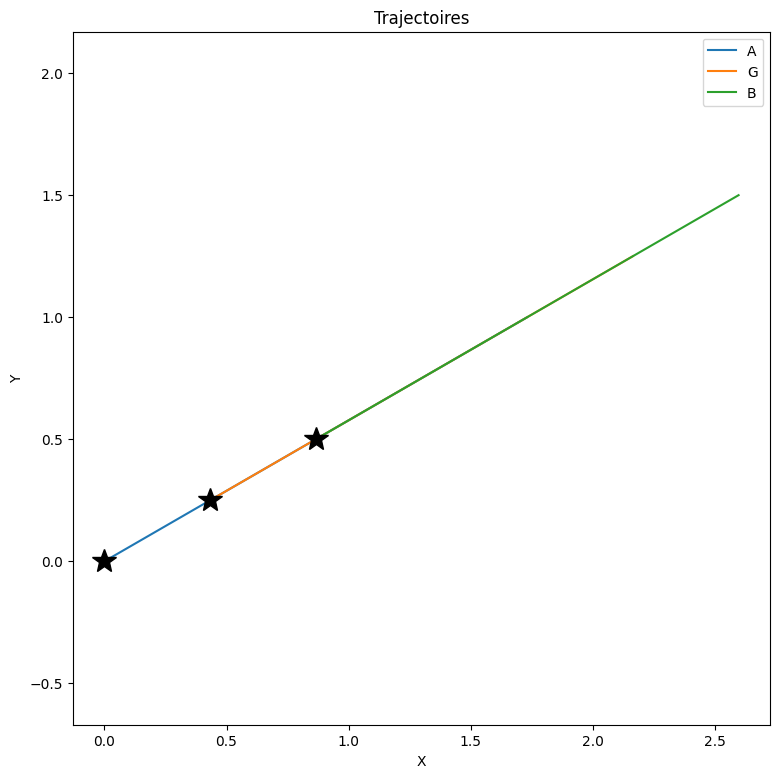
../../../../_images/c623e0bcce5bba5f62ba23454c4c1c85ed9dd33837fd63000eb89d3575007569.png 
trottinette.trajP1P2(t,tmax)
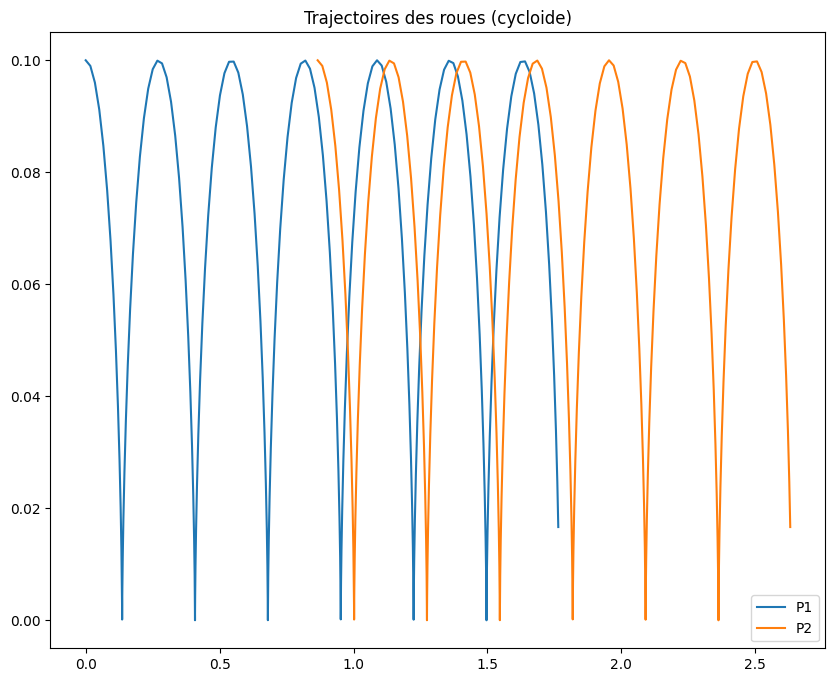
../../../../_images/ba3734a7378f9cc75e1670cd4e4832409dfa835f3e7bd17f352223ee25e6e38c.png

7.3.3. calcul des vitesses#

calculer l’expression numérique fonction de t de la vitesse de A et de P1 par rapport à R0 mais projeter dans R1 et mettre le résultat dans les variables VA et VP1. On utilisera la méthode .doit() pour forcer l’évaluation des vitesses.

# vérification
VA = 0
VP1 = 0
### BEGIN SOLUTION
VA  = A.vel(R0).express(R1).subs(cdtsNG).subs(valnum).doit()
VP1 = P1.vel(R0).express(R1).subs(cdtsNG).subs(valnum).doit()
### END SOLUTION

display("VA=",VA)
assert(VA == Vector.express(Point.vel(A,R0),R1).subs(cdtsNG).subs(valnum).doit())
display("VP1=",VP1)
assert(VP1 == Vector.express(Point.vel(P1,R0),R1).subs(cdtsNG).subs(valnum).doit())

'VA='
\[\displaystyle 0.27778\mathbf{\hat{r_1}_x}\]
'VP1='
\[\displaystyle (0.27778 \cos{\left(5.5556 t \right)} + 0.27778)\mathbf{\hat{r_1}_x} - 0.27778 \sin{\left(5.5556 t \right)}\mathbf{\hat{r_1}_z}\]
trottinette.vitesse([A,B,P1,P2],t,tmax)
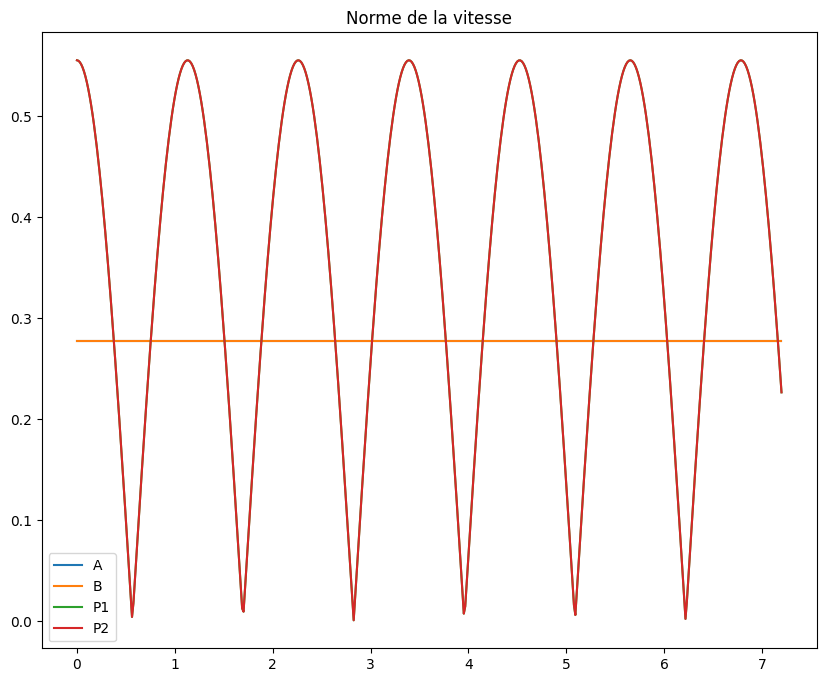
../../../../_images/42e2ec1cef4a0b77733749634f222a6cab40474e6bfb8729c9f8b275e1d41384.png

7.3.4. commentaires#

écrire ici vos commentaires (en double cliquant sur la cellule ci-dessous)

Ecrire ici commentaires

7.3.4.1. BEGIN SOLUTION#

7.3.4.2. END SOLUTION#

7.4. Cas d’une trajectoire circulaire de rayon R#

  • vitesse de rotation \(\Omega\)

  • \(x_a = R\cos(\Omega t) , y_a = R\sin(\Omega t)\)

  • \(\psi = \Omega t + \pi/2\)

  • \(u_a = \Omega R \)

7.4.1. conditions de roulement sans glissement#

Omega, R = sp.symbols("Omega R",positive=True)
cdts = [(psi,Omega*t+sp.pi/2),(ua,Omega*R),(xa,R*sp.cos(Omega*t)),(ya,R*sp.sin(Omega*t)),(phi,phi0)]
display("conditions mvt circulaire",cdts)

'conditions mvt circulaire'
\[\displaystyle \left[ \left( \psi, \ \Omega t + \frac{\pi}{2}\right), \ \left( u_{a}, \ \Omega R\right), \ \left( x_{a}, \ R \cos{\left(\Omega t \right)}\right), \ \left( y_{a}, \ R \sin{\left(\Omega t \right)}\right), \ \left( \phi, \ \phi_{0}\right)\right]\]
# conditions cinematiques
cdtsGL=[(theta1,omega1*t),(theta2,omega2*t),
        (omega1,omega1.subs(cdtsGL1).subs(cdts)),(phi0,phi0.subs(cdtsGL2).subs(cdts).simplify()),
        (omega2,omega2.subs(cdtsGL2).subs(cdts).simplify())]
display("conditions de roulement sans glissement",cdtsGL)

'conditions de roulement sans glissement'
\[\displaystyle \left[ \left( \theta_{1}, \ \omega_{1} t\right), \ \left( \theta_{2}, \ \omega_{2} t\right), \ \left( \omega_{1}, \ \frac{\Omega R}{r}\right), \ \left( \phi_{0}, \ - 2 \operatorname{atan}{\left(\frac{R - \sqrt{L^{2} + R^{2}}}{L} \right)}\right), \ \left( \omega_{2}, \ \frac{\Omega R}{r \cos{\left(\phi_{0} \right)}}\right)\right]\]

7.4.2. Calcul de position des points A et B#

en utilisants les conditions données par cdts et en utilisant la méthode .subs calculer la position des points A et B dans R0 et mettre le résultat dans les variables OA et OB.

Dans la seconde cellule, calculer la vitesse de A et celle de B par rapport à R0 mais projeter dans R1 et mettre le résultat dans les variables VA et VB

# calculer la position de A et B dans R0
OA = 0
OB = 0
### BEGIN SOLUTION
OA = A.pos_from(O).express(R0).subs(cdts)
OB = B.pos_from(O).express(R0).subs(cdts)
### END SOLUTION

display("OA=",OA)
assert(OA == Vector.express(Point.pos_from(A,O),R0).subs(cdts))
display("OB=",OB)
assert(OB == Vector.express(Point.pos_from(B,O),R0).subs(cdts))

'OA='
\[\displaystyle R \cos{\left(\Omega t \right)}\mathbf{\hat{r_0}_x} + R \sin{\left(\Omega t \right)}\mathbf{\hat{r_0}_y} + r\mathbf{\hat{r_0}_z}\]
'OB='
\[\displaystyle (- L \sin{\left(\Omega t \right)} + R \cos{\left(\Omega t \right)})\mathbf{\hat{r_0}_x} + (L \cos{\left(\Omega t \right)} + R \sin{\left(\Omega t \right)})\mathbf{\hat{r_0}_y} + r\mathbf{\hat{r_0}_z}\]
# calculer la vitesse de A et B projetté dans R1
VA = 0
VB = 0
### BEGIN SOLUTION
VA = A.vel(R0).express(R1).subs(cdts)
VB = B.vel(R0).express(R1).subs(cdts).doit()
### END SOLUTION

display("VA=",VA)
assert(VA == Vector.express(Point.vel(A,R0),R1).subs(cdts))
display("VB=",VB)
assert(VB == Vector.express(Point.vel(B,R0),R1).subs(cdts).doit())

'VA='
\[\displaystyle \Omega R\mathbf{\hat{r_1}_x}\]
'VB='
\[\displaystyle \Omega R\mathbf{\hat{r_1}_x} + L \Omega\mathbf{\hat{r_1}_y}\]

7.4.3. valeurs numériques des paramètres#

  • définitions des valeurs numériques des paramètres dans valnum

  • vérification en calculant la valeur numérique de la vitesse de la roue avant au point de contact

on prend pour \(\omega\) une valeur donnant une vitesse \(u_a\) de \(\approx 10 km/h\)

# parametres numériques en USI
valnum=[(L,1.),(r,0.05),(h,1.),(R,2),(Omega,15.*0.27/2)]
# d ou l'on deduit la valeur numérique des autres parametres
valnum.append((phi0,phi0.subs(cdtsGL).subs(valnum)))
valnum.append((omega2,omega2.subs(cdtsGL).subs(valnum)))
valnum.append((omega1,omega1.subs(cdtsGL).subs(valnum)))
display("valeurs numériques",valnum)

'valeurs numériques'
\[\displaystyle \left[ \left( L, \ 1.0\right), \ \left( r, \ 0.05\right), \ \left( h, \ 1.0\right), \ \left( R, \ 2\right), \ \left( \Omega, \ 2.025\right), \ \left( \phi_{0}, \ 0.463647609000806\right), \ \left( \omega_{2}, \ 90.5607530887415\right), \ \left( \omega_{1}, \ 81.0\right)\right]\]
# verification sur la vitesse de contacte de la roue avant
VG2.subs(cdts).subs(cdtsGL).subs(valnum).simplify()
\[\displaystyle - 1.66533453693773 \cdot 10^{-15}\mathbf{\hat{r_2}_x} - 8.88178419700125 \cdot 10^{-16}\mathbf{\hat{r_2}_y}\]

7.4.4. calcul numérique de la trajectoire de A et B#

En utilisant les conditions de mvt circulaire cdts , les conditions de roulement sans glissement cdtsGL et les valeurs numériques valnum, calculer la position de A et B dans R0 en fonction du temps à l’aide des méthodes .pos_from(), express() et .subs() et mettre le résultat dans les variables OA et OB

Que peut on en déduire ? (écrire les commentaires dans la cellule de texte suivante)

# position de A fct de t
OA = 0
# position de B fct de t
OB = 0
### BEGIN SOLUTION
OA = A.pos_from(O).express(R0).subs(cdts).subs(cdtsGL).subs(valnum)
OB = B.pos_from(O).express(R0).subs(cdts).subs(cdtsGL).subs(valnum)
### END SOLUTION

display("OA=",OA)
assert(OA == Vector.express(Point.pos_from(A,O),R0).subs(cdts).subs(cdtsGL).subs(valnum))
display("OB=",OB)
assert(OB == Vector.express(Point.pos_from(B,O),R0).subs(cdts).subs(cdtsGL).subs(valnum))

'OA='
\[\displaystyle 2 \cos{\left(2.025 t \right)}\mathbf{\hat{r_0}_x} + 2 \sin{\left(2.025 t \right)}\mathbf{\hat{r_0}_y} + 0.05\mathbf{\hat{r_0}_z}\]
'OB='
\[\displaystyle (- 1.0 \sin{\left(2.025 t \right)} + 2 \cos{\left(2.025 t \right)})\mathbf{\hat{r_0}_x} + (2 \sin{\left(2.025 t \right)} + 1.0 \cos{\left(2.025 t \right)})\mathbf{\hat{r_0}_y} + 0.05\mathbf{\hat{r_0}_z}\]

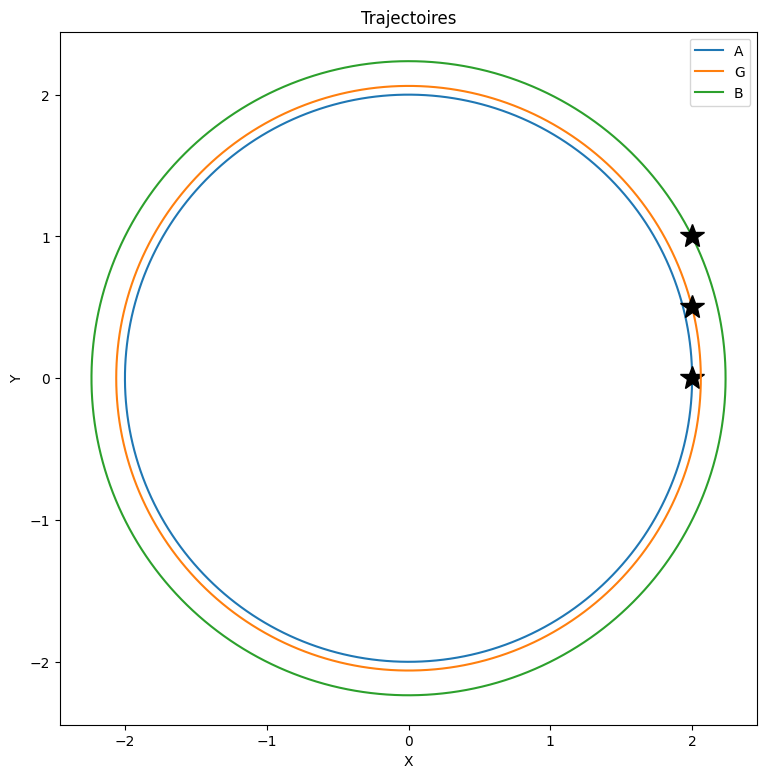
commentaires

# trajectoires des points A,B,G
trottinette =  Trottinette([O,A,B,G,P1,P2], [R0,R1], [r,h,L,R], cdts, cdtsGL, valnum)
# tmax 60. pour 1 tour
tmax = float(60./(Omega*30/np.pi).subs(valnum))
print("tmax=",tmax)
trottinette.traj2D([A,G,B],t,tmax)

tmax= 3.10280755910103
../../../../_images/fba14c7514d3409b3b0ead12328e0b3a6c9444d5477b297806f8f8fd9e753457.png

7.4.5. calcul numérique de la vitesse#

Calcul le module de la vitesse de A, B, P1 et P2 en fonction du temps en utilisant les méthodes .vel() .magnitude() et .subs() et en dernier .doit() pour forcer les évaluations, et mettre le résultat dans les variables VA, VB, VP1 et VP2

Que peut on en déduire ? (on écrirera les commentaires dans la cellule de texte suivante suivante)

# module de la vitesse de A
VA = 0
# module de la vitesse de B
VB = 0
# module de la vitesse de P1
VP1 = 0
# module de la vitesse de P2
VP2 = 0
### BEGIN SOLUTION
VA = A.vel(R0).magnitude().subs(cdts).subs(cdtsGL).subs(valnum)
VB = B.vel(R0).magnitude().subs(cdts).subs(cdtsGL).subs(valnum).doit()
VP1 = P1.vel(R0).magnitude().subs(cdts).subs(cdtsGL).subs(valnum).doit()
VP2 = P2.vel(R0).magnitude().subs(cdts).subs(cdtsGL).subs(valnum).doit()
### END SOLUTION

display("VA=",VA)
assert(VA == Vector.magnitude(Point.vel(A,R0)).subs(cdts).subs(cdtsGL).subs(valnum))
display("VB=",VB)
assert(VB == Vector.magnitude(Point.vel(B,R0)).subs(cdts).subs(cdtsGL).subs(valnum).doit())
display("VP1=",VP1)
assert(VP1 == Vector.magnitude(Point.vel(P1,R0)).subs(cdts).subs(cdtsGL).subs(valnum).doit())
display("VP2=",VP2)
assert(VP2 == Vector.magnitude(Point.vel(P2,R0)).subs(cdts).subs(cdtsGL).subs(valnum).doit())

'VA='
\[\displaystyle 4.05\]
'VB='
\[\displaystyle 4.52803765443708\]
'VP1='
\[\displaystyle 5.72756492761104 \sqrt{0.0003125 \sin^{2}{\left(81.0 t \right)} + \cos{\left(81.0 t \right)} + 1}\]
'VP2='
\[\displaystyle 6.40361226184097 \sqrt{0.00025 \sin^{2}{\left(90.5607530887415 t \right)} - 4.85722573273506 \cdot 10^{-18} \sin{\left(90.5607530887415 t \right)} + 1.0 \cos{\left(90.5607530887415 t \right)} + 1}\]
# tracer de la vitesse
trottinette.vitesse([A,B,P1,P2],t,tmax/5)
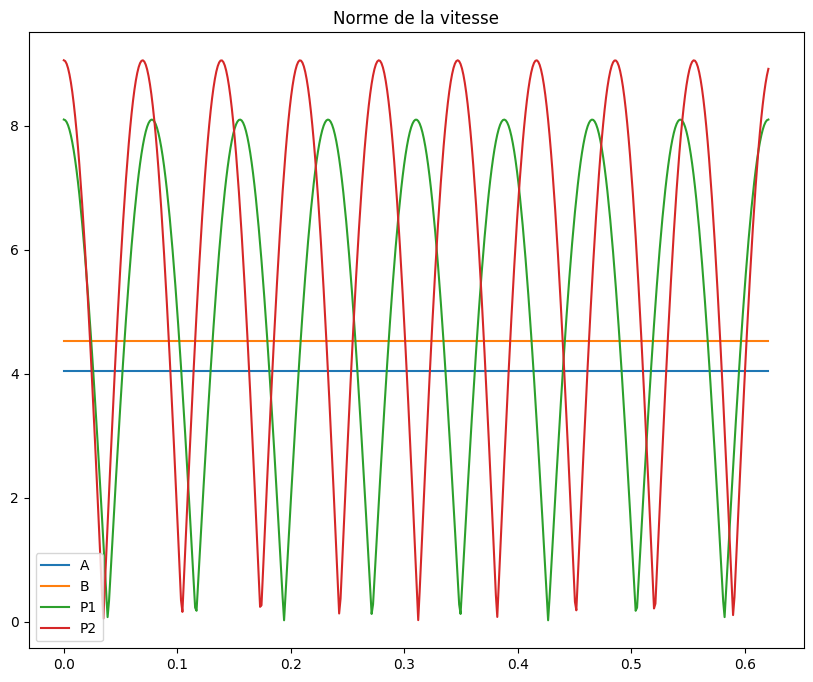
../../../../_images/ea7fe6d5fdc2f6405effe481b6ea57af4061346f289e17c2c55c26ec1996928a.png

Entrez ici vos commentaires

7.4.5.1. BEGIN SOLUTION#

7.4.5.2. END SOLUTION#

7.4.6. Calcul numérique de la trajectoire des roues, visualisation 3D#

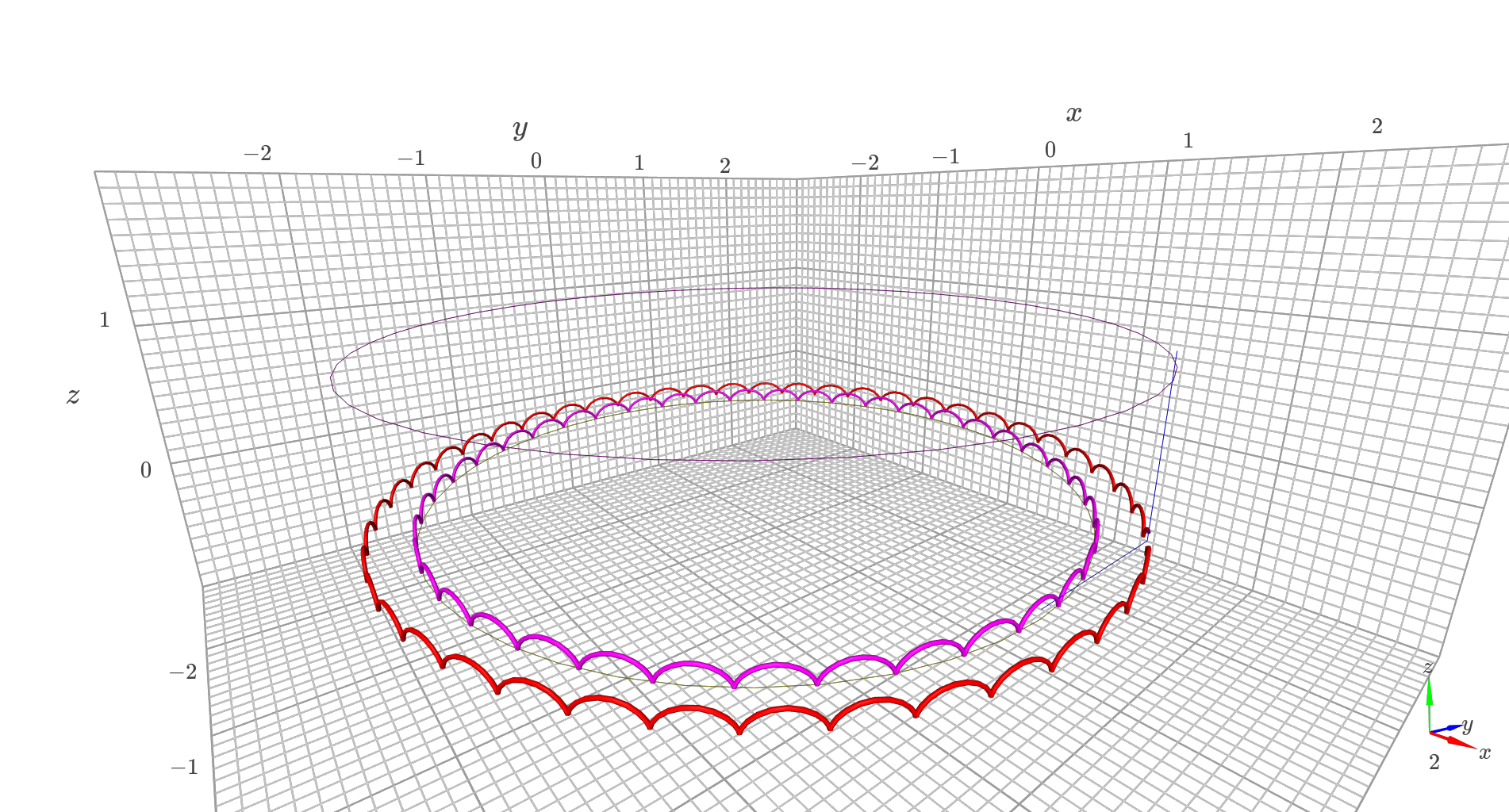
../../../../_images/traj3D_trottinette.png 
trottinette.traj3D(t,tmax)

7.4.7. analyse cinématique#

7.4.7.1. calcul de la norme des vitesses#

display("VA=",A.vel(R0).subs(cdts).magnitude())
display("VB=",B.vel(R0).subs(cdts).magnitude().simplify())
display("VG=",G.vel(R0).subs(cdts).magnitude().simplify())

'VA='
\[\displaystyle \Omega R\]
'VB='
\[\displaystyle \sqrt{L^{2} \Omega^{2} + \Omega^{2} R^{2}}\]
'VG='
\[\displaystyle \frac{\sqrt{L^{2} \Omega^{2} + 4 \Omega^{2} R^{2}}}{2}\]

7.4.7.2. calcul des accelérations A#

la trottinette est soumise à une accélération centripède, et donc le conducteur en G ressent une force centrifuge de direction opposée \(M\vec{\gamma}(G)\)

display("A(A)=",A.acc(R0).subs(cdts).simplify())
display("A(G)=",G.acc(R0).subs(cdts).simplify())
display("A(B)=",B.acc(R0).subs(cdts).simplify())

'A(A)='
\[\displaystyle \Omega^{2} R\mathbf{\hat{r_1}_y}\]
'A(G)='
\[\displaystyle - \frac{L \Omega^{2}}{2}\mathbf{\hat{r_1}_x} + \Omega^{2} R\mathbf{\hat{r_1}_y}\]
'A(B)='
\[\displaystyle - L \Omega^{2}\mathbf{\hat{r_1}_x} + \Omega^{2} R\mathbf{\hat{r_1}_y}\]

7.5. Analyse dynamique de la roue avant#

en assimilant la roue avant à un disque plein de masse \(m\) , de rayon \(r\) et de centre de gravité \(A\), on peut définir un solide rigide Roue en spécifiant

  • son centre de gravité \(B\)

  • le référentiel lié au solide \(R_4\)

  • la masse \(m\)

  • les moments d’inertie en \(B\) dans \(R_4\)

le moment d’inertie d’un disque par rapport à son centre vaut \(I_2 = \frac{m r^2}{2}\) suivant \(R_4.y\) et \(I_1 = \frac{m r^2}{4}\) suivant \(R_4.x\) et \(R_4.z\)

En utilisant la fonction ìnertia(frame,I1,I2,I3) et RigidBody, on définit le solide Roue comme ci-dessous:

from sympy.physics.mechanics import RigidBody, inertia
# parametres
m  = sp.symbols('m')
I1 = m*r**2/4
I2 = m*r**2/2
# moment d'inertie dans R4 (axes principales d'inertie)
IG = inertia(R4,I1,I2,I1)
# solide Roue
Roue = RigidBody('Roue',B, R4, m, (IG,B))

7.5.1. questions#

En utilisant les méthodes de Roue, calculer

  • la quantité de mouvement avec .linear_momentum(frame) par rapport à \(R_0\) et mettre le résultat dans la variable QB

  • le moment cinétique avec.angular_momentum(Point,frame) par rapport à \(R_0\) et mettre le résultat dans la variable SigmaB

  • projeté le résultat dans \(R_2\) avec substitution des conditions du mouvement cdts et cdtsGL, en forçant l’évaluation avec .doit() puis en simplifiant avec .simplify()

  • Analyser le résultat dans la cellule de texte suivante

QB=0
SigmaB=0
## BEGIN SOLUTION
QB = Roue.linear_momentum(R0).express(R2).subs(cdts).subs(cdtsGL).doit().simplify()
display(QB)
SigmaB = Roue.angular_momentum(B,R0).express(R2).subs(cdts).subs(cdtsGL).doit().simplify()
display(SigmaB)
## END SOLUTION
\[\displaystyle \frac{\Omega m \left(- L^{2} R + L^{2} \sqrt{L^{2} + R^{2}} - R^{3} + R^{2} \sqrt{L^{2} + R^{2}}\right)}{L^{2} + R^{2} - R \sqrt{L^{2} + R^{2}}}\mathbf{\hat{r_2}_x}\]
\[\displaystyle \frac{\Omega R m r}{2 \cos{\left(\phi_{0} \right)}}\mathbf{\hat{r_2}_y} + \frac{\Omega m r^{2}}{4}\mathbf{\hat{r_2}_z}\]
display("QB=",QB,"SigmaB=",SigmaB)
assert( QB.dot(R2.y) == 0  and QB.dot(R2.z) == 0 )
assert( SigmaB.dot(R2.x) == 0 )

'QB='
\[\displaystyle \frac{\Omega m \left(- L^{2} R + L^{2} \sqrt{L^{2} + R^{2}} - R^{3} + R^{2} \sqrt{L^{2} + R^{2}}\right)}{L^{2} + R^{2} - R \sqrt{L^{2} + R^{2}}}\mathbf{\hat{r_2}_x}\]
'SigmaB='
\[\displaystyle \frac{\Omega R m r}{2 \cos{\left(\phi_{0} \right)}}\mathbf{\hat{r_2}_y} + \frac{\Omega m r^{2}}{4}\mathbf{\hat{r_2}_z}\]

7.5.2. analyse#

7.5.2.1. BEGIN SOLUTION#

  • la quantité de mouvement est suivant R2.x avec un module constant \(\approx m \Omega R\), mais une direction qui varie

  • on a donc une accélération radiale (force centripéde)

  • pour créer cette accélération le conducteur doit pencher la trottinette vers l’intérieur du virage pour avoir une force de réaction non verticale.

  • le moment cinétique a une composante verticale constante (suivant R2.z)

  • mais une composante suivant R2.y avec un module constant mais une direction qui varie

  • il faut appliquer un couple gyroscopique \(Cg\) suivant R0.x $\( Cg \vec{R2.x} = \sigma \vec{R2.y} \wedge \Omega \vec{R2.z}\)$

7.5.2.2. END SOLUTION#

7.6. Etude simplifié de la dynamique de la trottinette en virage#

On applique les principes fondamentaux de la mécanique:

  • variation qte de mouvement = somme des forces

  • variation mt cinétique en G = somme des moments en G

  • moment en A d’une force \(\vec{F}\) appliquée en B $\( \vec{M_A} = \vec{AB}\wedge \vec{F}\)$

En négligeant les forces de frottement, les forces s’appliquant sur la trottinette et son conducteur sont:

  • le poids appliqué au centre de gravité G (du conducteur), dirigé suivant la verticale \(\vec{z}\)

  • la réaction du sol au point de contacte des roues dans le plan de chaque roue

  • la force motrice du moteur dans la direction du mouvement \(\vec{x}\)

En virage, on doit modifier l’orientation de la quantité de mouvement pour créer une accélération centripéde, mais aussi l’orientation du moment cinétique des roues.

Pour cela le conducteur va pencher la trottinette vers l’intérieur du virage en utilisant le guidon pour imprimer une rotation suivant \(\vec{R_2.x}\) et pas uniquement tourner le guidon autour de \(\vec{R_2.z}\). D’autre part, les roues ont un moment cinétique principalement suivant \(\vec{R_2.y}\) dont il faut changer la direction, i.e. le faire tourner autour de \(\vec{R_2.z}\). Pour cela il faut appliquer un couple gyroscopique suivant \(\vec{R_2.x}\) dans le sens opposé au mouvement de rotation précédent, ce qui limite (mais dans une faible mesure) l’angle de rotation autour de \(\vec{R_2.x}\). On constate donc que ce couple gyroscopique a un effet stabilisant, mais qui reste faible dans la pratique.

7.6.1. calcul de l’angle d’inclinaison de la trottinette#

Pour calculer l’angle \(\beta\) d’inclinaison de la trottinette,on suppose que le centre de gravité G (du conducteur) subit une rotation \(\beta\) autour de la direction \(R_1.x\) (direction de la vitesse), c.a.d le conducteur de masse M se penche à droite ou à gauche.

On se place dans le référentiel lié au conducteur \(R_1\), dans lequel le conducteur est immobile. \(R_1.x\) est dans la direction de la vitesse, \(R_1.y\) est dirigée vers le centre du virage, et \(R_1.z\) est vertical.

Les forces qui s’exercent sont:

  • le poids \(\vec{P}\) en G suivant la verticale \(R_1.z\) : $\(\vec{P}= -M g \vec{R_1.z}\)$

  • la réaction du sol \(\vec{Fr}\) sur les roues qui est inclinée de \(\beta\) par rapport à la verticale: $\(\vec{Fr}= F \left(\sin{\beta} \vec{R_1.x} + \cos{\beta} \vec{R_1.z}\right)\)$

  • la force centrifuge \(\vec{Fc}\) suivant l’horizontale avec une composante principale suivant \(R_1.y\) $\(\vec{Fc}= - M \vec{\gamma}(G)_{|R_0} \)$

  • la force motrice suivant \(R_1.x\) (direction de la vitesse) qui permet de vaincre les frottements.

L’équilibre dans \(R_1\) impose donc : $\( \vec{P} + \vec{Fr} + \vec{Fc} = \vec{0}\)$

beta, M, g, F = sp.symbols('beta M g F')
# force centrifuge
Fc = -M*G.acc(R0).subs(cdts).simplify()
display('force centrifuge=',Fc)
Fc = Fc.dot(R1.y)*R1.y
display('force centrifuge=',Fc)
# force de gravité
P = - M*g*R1.z
# reaction
Fr = F*(sp.cos(beta)*R1.z + sp.sin(beta)*R1.y)
display('réaction du sol=',Fr)
# bilan: somme des forces
S = P + Fr + Fc
display("bilan=",S)
eq1 = sp.Eq(sp.tan(beta),Omega**2*R/g)
eq2 = sp.Eq(F,M*g/sp.cos(beta))
display("solution",eq1,eq2)

'force centrifuge='
\[\displaystyle \frac{L M \Omega^{2}}{2}\mathbf{\hat{r_1}_x} - M \Omega^{2} R\mathbf{\hat{r_1}_y}\]
'force centrifuge='
\[\displaystyle - M \Omega^{2} R\mathbf{\hat{r_1}_y}\]
'réaction du sol='
\[\displaystyle F \sin{\left(\beta \right)}\mathbf{\hat{r_1}_y} + F \cos{\left(\beta \right)}\mathbf{\hat{r_1}_z}\]
'bilan='
\[\displaystyle (F \sin{\left(\beta \right)} - M \Omega^{2} R)\mathbf{\hat{r_1}_y} + (F \cos{\left(\beta \right)} - M g)\mathbf{\hat{r_1}_z}\]
'solution'
\[\displaystyle \tan{\left(\beta \right)} = \frac{\Omega^{2} R}{g}\]
\[\displaystyle F = \frac{M g}{\cos{\left(\beta \right)}}\]

7.6.2. Analyse#

Donc le conducteur doit se pencher vers l’intérieur du cercle, i.e. \(\beta >0 \), pour contrer la force centrifuge.

L’inclinaison optimale a été obtenue ci-dessus. En supposant que \(R\gg L,h\), on peut calculer l’expression de \(\beta\) en fonction des paramètres du problème, en particulier \(u_a\) et \(R\). Mettre le résultat dans la variable bopt, puis calculer sa valeur numérique en degré dans bval en substituant les valeurs numériques des paramètres avec \( g = 9.81\). On calculera la valeur numérique en degré avec 2 chiffres significatifs en utilisant la méthode .evalf(2)

bopt = 0
bval = 0
### BEGIN SOLUTION
bopt =  sp.atan(ua**2/g/R)
bval = (bopt.subs(cdts).subs(valnum).subs(g,9.81)*180/np.pi).evalf(2)
### END SOLUTION

display("Beta opt=",bopt)
print("valeur en degré=",bval)
assert(np.abs(sp.N(bopt.subs(cdts).subs(valnum).subs(g,9.81))-np.radians(float(bval))) < 0.01)

'Beta opt='
\[\displaystyle \operatorname{atan}{\left(\frac{u_{a}^{2}}{R g} \right)}\]
valeur en degré= 40.

7.7. Conclusion#

Ecrire dans la cellule de texte suivante vos conclusions sur cette étude, en particulier sur le résultat obtenu pour \(\beta\) et sa dépendance aux paramètres, en particulier par rapport à la masse du conducteur , la hauteur du centre de gravité ou le rayon du cercle.

7.7.1. vos commentaires#

  • Pour une vitesse de l’ordre de \(15 km/h\) , que peut on dire de l’angle d’inclinaison !!!

  • Comparez à un vélo !

7.7.1.1. BEGIN SOLUTION#

en virage, sur une trottinette

  • il faut absolument la pencher vers l’intérieur du virage

  • l’angle est proportionnel au carré de la vitesse \(u_a\) et inversement proportionnel au rayon de courbure \(R\)

  • une trottinette est beaucoups moins stable qu’un vélo !

7.7.1.2. END SOLUTION#

7.8. FIN du TP#

Contenu