8. Roulement sans glissement d’une meule#
Marc Buffat département mécanique Lyon 1
8.1. Objectifs#
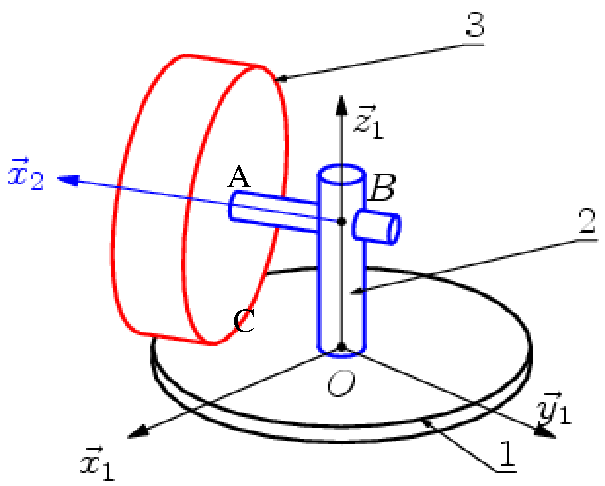
On étudie la cinématique d’une meule de rayon \(r\), accrochée à une tige horizontale de longueur \(d\) entraînée en rotation autour d’un axe vertical.
Soit \(R_1\) un repère fixe d’axe vertical \(\vec{Z}_1\). On note \(\vec{OB} = r \vec{Z}_1\) l’axe de rotation vertical de la meule, \(\theta(t)\) l’angle de rotation de la tige horizontale \(BA\). On note \(R_2\) le repère lié à la tige \(BA\) en rotation \(\theta\) autour de l’axe vertical. On a \(\vec{BA} = d \vec{X}_2\). Enfin la meule est en rotation d’angle \(\phi\) autour de cette tige \(BA\) et on note \(R_3\) le repère lié à la meule. On note \(C\) le point de contact de la meule avec le sol, et on suppose que le roulement de la meule sur le sol est sans glissement. On a \(\vec{CA} = r \vec{Z_1}\)
Les 2 degrés de liberté du système sont les 2 angles:
\(\theta(t)\) l’angle de rotation autour de la verticale \(Z_{1}\)
\(\phi(t)\) l’angle de rotation de la meule autour de \(X_{2}\)
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
# bibliotheque mecanique
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum
from sympy.physics.vector import time_derivative,dot
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
#
from IPython.display import display, Markdown, clear_output
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
from validation.validation import info_etudiant
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
printmd("**ERREUR**: numéro d'étudiant non spécifié!!!")
NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
#raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Etudiant {} {} id={}**".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_r = 1+np.random.randint(9)
_d = 1+np.random.randint(9)
_omega = 1+np.random.randint(9)
printmd("Paramétres de l'étude: r={} d={} omega={}".format(_r,_d,_omega))
ERREUR: numéro d’étudiant non spécifié!!!
Etudiant Marc BUFFAT id=137764122
Paramétres de l’étude: r=4 d=3 omega=7
8.2. Modèle mécanique#
on définit les paramêtres du problème: le rayon \(r\) et la longueur \(d\)
on définit les degrés de liberté: \(\theta(t), \phi(t)\)
on définit les repères \(R_1, R_2, R_3\)
8.2.1. parametres du problème#
# parametres du problème: rayon masse du cerceau position masse
r,d,t = sp.symbols('r d t')
# degrés de liberté
theta = dynamicsymbols('theta')
phi = dynamicsymbols('phi')
8.2.2. Repères et positions#
un repère fixe \(R_1\)
un repère mobile lié à la tige \(AB\) : \(R_2\)
un repère mobile lié à la meule \(R_3\)
les points \(O\), \(B\) et \(A\)
on note \(P\) un point sur la périphérie de la meule: \(\vec{CA} = r \vec{Z_3}\)
# repère
R1 = ReferenceFrame('R_1')
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[theta, R1.z])
R3 = ReferenceFrame('R_3')
R3.orient(R2,'Axis',[phi, R2.x])
8.2.3. question 1#
définir la position des points A, B et P en utilisant la méthode .set_pos(point, vecteur position)
# points
O = Point('O')
A = Point('A')
B = Point('B')
P = Point('P')
### BEGIN SOLUTION
B.set_pos(O,r*R1.z)
A.set_pos(B,d*R2.x)
P.set_pos(A,r*R3.z)
### END SOLUTION
display("OA=",A.pos_from(O),"OB=",B.pos_from(O),"OP=",P.pos_from(O))
assert(B.pos_from(O).dot(R1.z) == r)
assert(A.pos_from(O).dot(R2.x) == d)
assert(P.pos_from(A).dot(R3.z) == r)
'OA='
'OB='
'OP='
8.3. Etude cinématique#
application de la composition des vitesses
Si les 2 points M et P sont fixes dans le repère \(R_1\) et on connaît la vitesse de M par rapport à un autre repère \(R_0\), alors on utilise la méthode P.v2pt_theory(M,R0,R1)
8.3.1. question 2#
En utilisant la composition de vitesse, calculer dans la cellule suivante la vitesse du point A et P par rapport à R0 sachant que :
\(\vec{V}_O/R_1 = 0\)
\(\vec{V}_B/R_1 = 0\)
\(\vec{V}_A/R_2 = 0\)
\(\vec{V}_P/R_3 = 0\)
# definition et calcul des vitesses
O.set_vel(R1,0.)
B.set_vel(R1,0.)
A.set_vel(R2,0.)
P.set_vel(R3,0.)
# calcul de la vitesse de A,B et P dans R0
### BEGIN SOLUTION
A.v2pt_theory(B,R1,R2)
P.v2pt_theory(A,R1,R3)
### END SOLUTION
display("VA=",A.vel(R1),"VP=",P.vel(R1))
assert(A.vel(R1).dot(R2.y) == d*theta.diff(t))
assert(P.vel(R1).dot(R3.x) == r*sp.sin(phi)*theta.diff(t))
'VA='
'VP='
8.4. projection des vitesses dans différents repères#
8.4.1. question 3#
en utilisant les méthodes .express(repere) et .simplify() , calculer la vitesse de P / à R1 projetté dans R1 puis dans R2 et mettre le résultat dans les variables VP1 et VP2
# composantes de VP dans R1 et R2
VP1 = 0
VP2 = 0
### BEGIN SOLUTION
VP=P.vel(R1)
VP1 = VP.express(R1).simplify()
VP2 = VP.express(R2).simplify()
### END SOLUTION
display("VP1+",VP1,"VP2=",VP2)
assert (VP1.dot(R1.z) == -r*sp.sin(phi)*phi.diff(t))
assert (VP2.dot(R2.z) == -r*sp.sin(phi)*phi.diff(t))
'VP1+'
'VP2='
8.5. Condition de roulement sans glissement#
La condition de roulement sans glissement du disque de la meule implique :
d’où une condition entre les vitesses de rotation de la meule \(\dot{\phi}=\Omega\) et \(\dot{\theta}=\omega\), ce qui permet d’exprimer \(\omega\) en fonction de \(\Omega\).
8.5.1. question 4#
Calculer dans la variable Vg la vitesse de glissement du disque, i.e. la vitesse de P pour \(\phi = \pi\) en notant \(\Omega=\dot{\phi}\) la vitesse de rotation de la meule autour de \(R_2.x\)
On utilisera la méthode
.subs([(phi.diff(t),Omega),(phi,sp.pi)])
pour faire les substitutions. En déduire l’expression de \(\dot{\theta}\) la vitesse rotation de la meule autour de \(R_1.z\) en fonction de \(\Omega\) et mettre le résultat dans la variable omega.
Omega = sp.symbols('Omega')
Vg = 0
### BEGIN SOLUTION
Vg=VP.express(R2).simplify().subs([(phi.diff(t),Omega),(phi,sp.pi)])
display(Vg)
omega = sp.solve(Vg.dot(R2.y),theta.diff(t))[0]
### END SOLUTION
display("omega=",omega, " Vg=",Vg.subs(theta.diff(t),omega))
assert(Vg.subs(theta.diff(t),omega) == 0)
'omega='
' Vg='
8.6. Trajectoires#
on suppose une rotation uniforme de la meule \(\dot{\theta}=\omega=cste\).
En déduire la valeur de \(\Omega=\dot{\phi}\) et déterminer l’expression de \(\phi\) et \(\theta\) en fonction de t.
En utilisant les valeurs numériques de r, d et \(\omega\) ci dessous, on va calculer l’expression de A et de P dans R1 en fonction uniquement de t.
8.6.1. question 5#
Pour cela définir l’expression de \(\phi\) et \(\theta\) dans la variable vals (on remplace la valeur 0 par la bonne expression), puis la valeur des paramètres numériques (r,d et \(\Omega\)) dans valnum.
En déduire la position de A et de P dans R1 en fonction uniquement de t (les autres paramètres ayant été substitués). On écrira le résultat respectivement dans la variable OA et OP. On pourra utilise les méthode .pos_from(point), .express(repère), .subs(vals) et .subs(valnum)
On donnera enfin la valeur tmax du temps d’étude de la trajectoire correspondant à une rotation de la meule autour de \(R1.z\)
printmd("valeurs des parametres: r={} d={} omega={}".format(_r,_d,_omega))
valeurs des parametres: r=4 d=3 omega=7
# définitions des paramétres du mouvement
vals = [(phi,0),(theta,0)]
# puis des parametres numériques
valnum = [(r,0),(d,0),(Omega,0)]
# calcul de la position de A et P dans R1 fonction de t uniquement
OA = 0
OP = 0
# temps d'étude (1 tour autour de R1.z)
tmax = 0
### BEGIN SOLUTION
valnum = [(r,_r), (d,_d), (Omega,-_omega*_d/_r) ]
display(valnum)
vals =[(phi, Omega*t),(theta,-Omega*r/d*t)]
display(vals)
OA = A.pos_from(O).express(R1).subs(vals).subs(valnum)
OP = P.pos_from(O).express(R1).subs(vals).subs(valnum)
tmax = 2*2*np.pi/_omega
### END SOLUTION
print("tmax={:.2f}".format(tmax))
display("valnums=",valnum,"vals=",vals)
display("OA=",OA,"OP=",OP)
assert (t in OP.dot(R1.x).free_symbols)
assert (t in OP.dot(R1.y).free_symbols)
assert (t in OP.dot(R1.z).free_symbols)
tmax=1.80
'valnums='
'vals='
'OA='
'OP='
8.6.2. Tracer des trajectoires#
# tracer des coordonnees fct de t
from validation.Traj3D import Traj3D
T3d = Traj3D([OA,OP],R1,t,tmax)
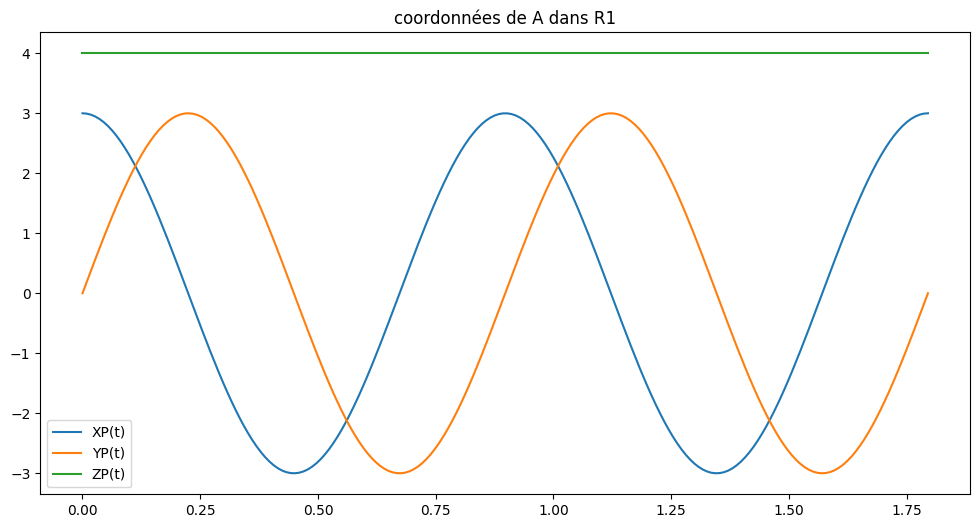
T3d.plot("coordonnées de A dans R1",0)
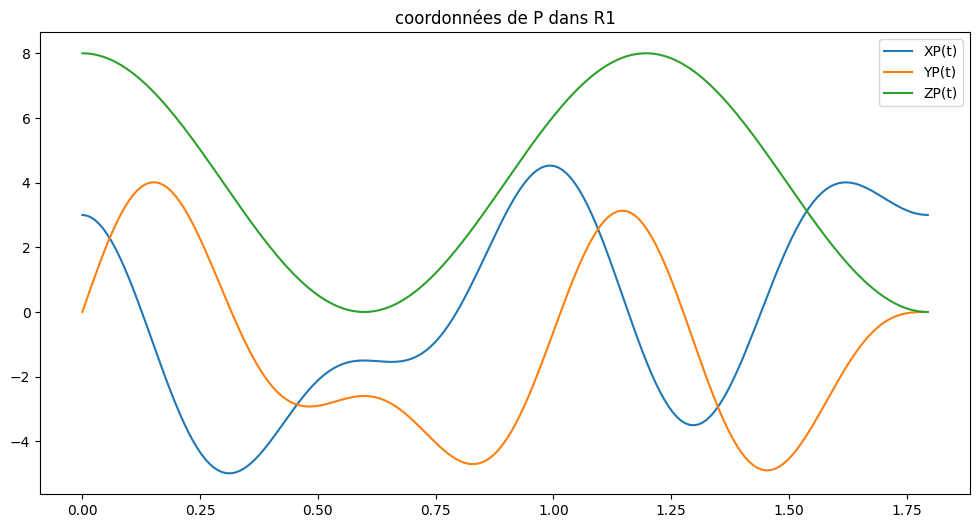
T3d.plot("coordonnées de P dans R1",1)
# trajectoire en 3D du point P
T3d.plot3D(1.2*_d,1,"Point P")
# Trajectoire du point A
T3d.plot3D(1.2*_d,0,"Point A")
8.7. Calcul des vitesses#
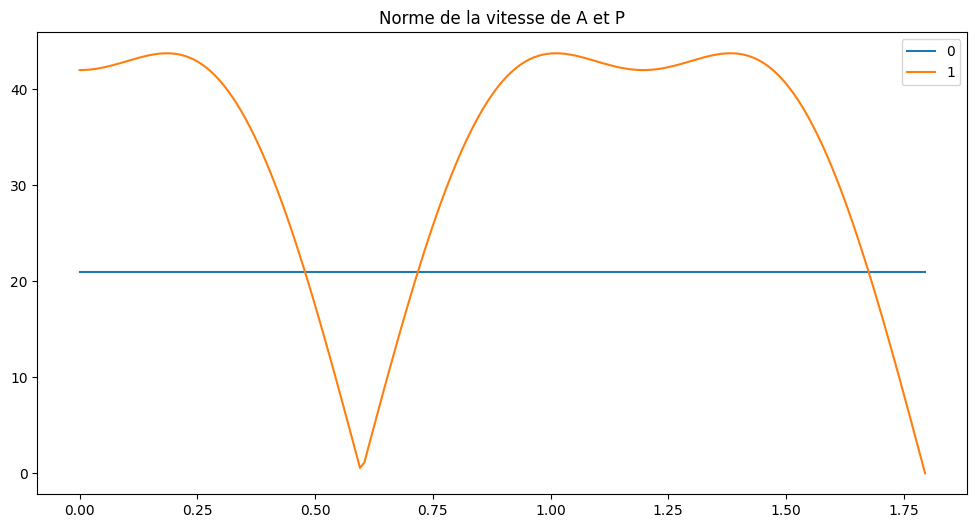
On s’intéresse maintenant à la norme de la vitesse de A et de P.
8.7.1. question 6:#
calculer la norme de la vitesse de A et de P et mettre l’expression dans les 2 variables VA et VP.
On pourra utiliser la méthode .vel(R1) puis .magnitude() pour calculer l’amplitude de la vitesse, puis la méthode .subs(vals).subs(valnum).doit() pour substituer dans l’expression les valeurs numériques fonctions de t de \(\theta\), \(\phi\) ainsi que la valeur de R et d.
# norme de la vitesse de A et P fonction de t
VA = 0
VP = 0
### BEGIN SOLUTION
VA = A.vel(R1).magnitude().subs(vals).subs(valnum).doit()
VP = P.vel(R1).magnitude().subs(vals).subs(valnum).doit()
### END SOLUTION
display("VA=",VA,"VP=",VP)
'VA='
'VP='
T3d.plotvit([VA,VP],"Norme de la vitesse de A et P")
8.8. Analyse du mouvement#
écrire vos commentaires ici en analysant la trajectoire de A et de P
8.8.1. Analyse de la trajectoire de A et de sa vitesse#
8.8.2. Analyse de la trajectoire de P et de sa vitesse#
8.9. Analyse dynamique de la meule#
en assimilant la meule à un disque plein de masse \(M\) , de rayon \(r\) et de centre de gravité \(A\), on peut définir un solide rigide S en spécifiant
son centre de gravité \(A\)
le référentiel lié au solide \(R_3\)
la masse \(M\)
les moments d’inertie en \(A\) dans \(R_3\)
le moment d’inertie d’un disque t par rapport à son centre vaut \(I_1 = \frac{M r^2}{2}\) suivant l’axe perpendiculaire au disque \(R_3.x\) et \(I_2 = \frac{M r^2}{4}\) par rapport aux 2 autres axes \(R_3.y\) et \(R_3.z\)
En utilisant la fonction ìnertia(frame,I1,I2,I3) et RigidBody, on définit le solide S comme ci-dessous:
from sympy.physics.mechanics import RigidBody, inertia
# parametres
M = sp.symbols('M')
I1 = M*r**2/2
I2 = M*r**2/4
# moment d'inertie dans R3 (axes principales d'inertie)
IG = inertia(R3,I1,I2,I2)
# solide S
S = RigidBody('S',A, R3, M, (IG,A))
8.9.1. questions#
En utilisant les méthodes de S, calculer
la quantité de mouvement avec
.linear_momentum(frame)par rapport à \(𝑅_1\) et mettre le résultat dans la variableQAle moment cinétique en A avec
.angular_momentum(Point,frame)par rapport à \(𝑅_1\) et mettre le résultat dans la variableSigmaAprojeté le résultat dans \(𝑅_2\) avec substitution des conditions du mouvement
vals, en simplifiant avec.simplify()puis en forçant l’évaluation avec.doit()
QA = 0
SigmaA = 0
## BEGIN SOLUTION
QA = S.linear_momentum(R1).express(R2).subs(vals).doit()
SigmaA = S.angular_momentum(A,R1).express(R2).subs(vals).simplify().doit()
## END SOLUTION
display("QA=",QA)
display("SigmaA=",SigmaA)
assert( QA.dot(R2.x) == 0 and QA.dot(R2.y) != 0 and QA.dot(R2.z) == 0)
assert( SigmaA.dot(R2.x) != 0 and SigmaA.dot(R2.y) == 0 and SigmaA.dot(R2.z) != 0)
'QA='
'SigmaA='
8.9.2. Accélération et forces#
calculer l’accélération de A dans \(R_1\) projeté dans \(R_2\) en tenant compte des conditions du mouvement
mettre le résultat dans la variable
GAen déduire l’expression vectorielle des différentes forces qui s’exercent sur la meule que l’on affectera aux variables spécifiées:
le poids dans la variable
Pla réaction du sol dans la variable
Fsla force centrifuge dans la la vraible
Fcla force de liaison dans la variable
Fl
Ecrire votre analyse dans la cellule de texte suivante
g = sp.symbols('g')
GA = 0
P = 0
Fs = 0
Fc = 0
Fl = 0
## BEGIN SOLUTION
GA = A.acc(R1).subs(vals).doit()
P = -M*g*R2.z
Fs = -P
Fc = -M*GA
Fl = -Fc
## END SOLUTION
display("GA=",GA)
display("P=",P,"Fs=",Fs,"Fc=",Fc,"Fl=",Fl)
assert(GA.dot(R2.x)!=0 and GA.dot(R2.y)==0 and GA.dot(R2.z)==0)
assert(P.dot(R2.z) != 0)
assert(Fc.dot(R2.x) != 0)
assert(P + Fs + Fc + Fl == 0)
'GA='
'P='
'Fs='
'Fc='
'Fl='
8.10. Compte rendu#
8.10.1. Analyse du résultat#
Ecrire votre analyse sur le bilan des forces qui s’exercent sur la meule.
8.10.2. Conclusion#
Ecrire votre conclusion sur cette étude
