11. TP: expérience du Brachistochrone#
# La ligne ""%matplotlib notebook" permet d'activer la possibilité d'interagir avec un graphique (zoom, affichage du pixel) ...
%matplotlib notebook
# Importation des bibliothèques utiles pour le TP.
import numpy as np
import matplotlib.pyplot as plt
# utilisation de opencv + efficace
import cv2
plt.rc('font', family='serif', size='18')
from validation.validation import info_etudiant
from validation.valide_markdown import test_markdown, test_code
from IPython.display import display, Markdown, clear_output
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("## Etudiant {} {} id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
11.1. Expérience du brachistochrone#
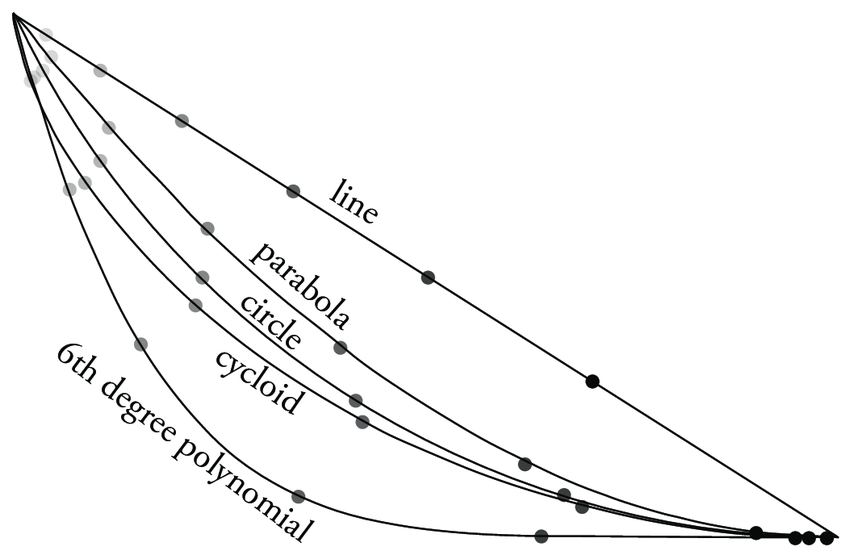
Le Brachistochrone (temps le plus court en grec ancien) est le nom donné à une expérience qui permet de montrer que le chemin le plus rapide n’est pas toujours celui que l’on croît ! Nous avons repris les images d’une expérience réalisée à l’EPFL en Suisse. L’expérience a été filmée avec une caméra rapide avec 940 images par seconde.

Les boules partent au même moment avec une vitesse initiale nulle. Après avoir constaté l’ordre d’arrivée des boules, on souhaite analyser plus en détail cette expérience:
Tout d’abord on va étudier le déplacement d’une boule roulant sur un plan incliné (boule blanche). On va comparer cette expérience à un modèle théorique.
Ensuite, on étudiera chaque trajectoire et on calculera sa longueur. On estimera ainsi la vitesse moyenne de chaque boule entre le point de départ et le point d’arrivée.
11.2. Mouvement d’une boule sur un plan incliné. Boule blanche#
On ne s’intéresse, dans un premier temps, qu’à la boule blanche qui est placée sur le plan incliné. En négligeant la contribution des forces de frottement mais en tenant compte de l’inertie de la boule, il est possible de montrer que la distance horizontale parcourue \(x(t)\) évolue comme :
où \(g=9.81 m/s^2\) est l’accélération de la gravité, \(\alpha\) est l’angle entre le plan incliné et l’horizontale, et \(t\) est le temps compté depuis le lâcher de la boule.
Nous allons calculer la valeur de \(K\) qui permet d’approcher au mieux les mesures de l’expérience.
11.2.1. calcul des paramètres#
Lisez l’image
brachistochroneSolo.pngavec la fonctioncv2.imreadet affichez-la dans une fenêtre graphique avecplt.imshow(de la bibliothèque matplotlib).En survolant avec votre souris l’image, relevez les coordonnées en pixel de la base de la plaque en bois qui nous sert d’étalon. La base du triangle est indiquée par la flèche rouge sur la figure de l’énoncé. Notez les valeurs relevées en pixel du début de la base de la plaque et de la fin de la base de la plaque. Calculez
Lpixla longueur de la base de la plaque en pixel et déduiseztaillepixla taille d’un pixel de l’image en mètres, sachant que la largeur de la plaque en bois vaut \(L=0.80m\). Vous expliquerez dans votre compte-rendu comment vous avez fait les conversions pour passer d’une mesure en pixel à une mesure en mètres.
Remarque : Pour plus de précision on peut zoomer sur l’image.
%matplotlib notebook
# Paramètres du problème
g = 9.81
fps = 940 # Nombre d'images par seconde (frame per sec)
larg_sousim_pix = 1280 # nombre de pixels dans la direction X pour une image
L = 0.8 # largeur de la base de la plaque en metres
# calcul a faire
taillepix = 0
#Lpix = # On mettra la valeur de L relevée en Pixel dans la variable Lpix
### BEGIN SOLUTION
# Les coordonnées 923 et 38 ont été relevées en pixel. Ce sont uniquement les coordonnées en x qui sont utiles.
### END SOLUTION
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif1',['plt.imshow(','imread(']))
assert(np.abs(L-taillepix*Lpix)<1.e-05)
11.2.2. mesures#
Pour construire l’image multiple
'brachistochrone9.png', nous avons retenu 9 images sur les 649 images du film. Cette image multiple de 2160x3840 pixels est constituée de 9 sous images de 720x1280 pixels. Il y a 3 lignes et 3 colonnes. Le temps défile en parcourant les images du haut en bas puis de gauche à droite.Affichez l’image
'brachistochrone9.png'dans une nouvelle figure.A l’aide du graphe interactif, relevez (en pixels) sur l’image les positions horizontales aux différents instants de la boule blanche.
Vous mettrez dans un tableau
numpyappeléxpixel, les 9 valeurs ainsi relevées.On appelle \(x(t)\) la distance horizontale de la boule aux temps t successifs. La première image de la boule correspond au point \(x=0\). Utiliser la taille d’un pixel calculée précédemment, et si besoin la taille des sous-images pour en déduire les 9 valeurs successives de \(x(t)\) en mètres et les mettre dans un tableau
xbr.
Faire attention à ce que chaque fois que l’on change de colonne d’images, l’origine en pixels pour la coordonnée x est modifiée. Il faut donc soustraire une largeur de sous image à chaque changement de colonne.
%matplotlib notebook
xpixel = None
xbr = None
### BEGIN SOLUTION
# On soustrait la largeur de la sous-image pour les sous images des col 2 et 3
### END SOLUTION
assert((xbr.size == 9) and (xpixel.size==9))
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif2',['plt.imshow(','imread(']))
11.2.3. tracé des mesures en fonction du temps#
Les images sont retenues toutes les 81 images. Le film est pris à 940 images par seconde. Construisez le tableau
tvecqui contient les valeurs successives des temps de chacune des images sur l’image multiple. Ce tableau a 9 éléments: le nombre de prises de vue sélectionnées. Pour la première image on fixe \(t=0\).Tracez sur une nouvelle figure, la courbe de \(x\) (en mètres) en fonction de \(t\) (en secondes). Annotez votre graphique : label de la courbe et axes, mettre les unités.
%matplotlib inline
tvec = None
### BEGIN SOLUTION
### END SOLUTION
assert((xbr.size == 9) and (xpixel.size==9))
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif3',['plt.plot(','plt.legend(','plt.xlabel','plt.ylabel']))
11.2.4. comparaison au modèle théorique#
Nous allons maintenant comparer ce graphique expérimental avec le modèle théorique
A l’aide de l’image brachistochroneSolo.png, en mesurant la hauteur \(H\), trouvez l’angle \(\alpha\) en radians que fait le plan incliné avec l’horizontale.
On mettra le résultat dans une variable alpha
alpha = 0.0
### BEGIN SOLUTION
#En faisant le rapport des distances en pixel lues on trouve l'angle
### END SOLUTION
print("Alpha={:.2f} radian".format(alpha))
assert((alpha>0.5) and (alpha<0.7))
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif4',['arctan']))
On veut ajuster les valeurs expérimentales avec une courbe:
On choisit une première valeur test de \(K=K_{test}=0.45\).
Superposez la courbe expérimentale avec la formule théorique (avec \(K_{test}\)). On mettra les valeurs de la formule théorique dans un tableau
xtestAjoutez une légende.
Etes-vous satisfait de ce résultat?
# Loi theorique avec Ktest=0.45
Ktest = 0.45
xtest = None
### BEGIN SOLUTION
#la courbe semble assez proche mais on doit pouvoir faire mieux.
### END SOLUTION
assert(xtest.size==9)
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif5',['plt.plot(','plt.legend(','plt.xlabel','plt.ylabel']))
11.2.5. quantification de l’erreur#
Pour quantifier l’erreur entre les courbes expérimentale et théorique pour \(K_{test}\), on la calcule au sens des moindres carrés :
Que vaut \(E\) pour \(K_{test}\)?
E = 0
### BEGIN SOLUTION
# Erreur au sens des moindres carrés
### END SOLUTION
print("Pour K "+str(Ktest)+" l'erreur vaut : " + str(E) )
assert(E>0)
11.2.6. Ajustement du modèle#
Amélioration du modèle : On veut maintenant déterminer quelle valeur de \(K\) permet d’approcher au mieux la courbe expérimentale au sens des moindres carrés. Pour cela on calcule l’erreur avec le modèle pour différentes valeurs de \(K\), puis on trace l’évolution de cette erreur en fonction de \(K\) pour déterminer la meilleur valeur.
Faire varier \(K\) entre \(0.25\) et \(0.50\), avec un pas de \(0.005\) en créant un tableau de valeurs
Kval.Calculer l’erreur pour ces valeurs dans la variable
ErrTracer cette erreur \(E\) en fonction de \(K\), et identifier la valeur optimale \(K_{opt}\) qui permet de minimiser l’erreur au sens des moindres carrés.
On pourra utiliser la fonction numy argmin
On mettra la valeur optimale trouvée dans Kopt
Err = None
Kval = None
Kopt = 0.0
### BEGIN SOLUTION
# Minimisation de l'erreur
### END SOLUTION
assert(Err.size == Kval.size)
#assert(Kopt == np.min(Kval))
11.2.7. comparaison expérience / modèle#
Superposer la courbe expérimentale avec la formule théorique obtenue avec \(K_{opt}\).
Ajouter une légende.
La théorie donne \(K_{theo}=5/14\). Quel est l’écart entre \(K_{opt}\) et \(K_{theo}\)?
Que pensez-vous que cet écart entre dans les incertitudes de mesure?
### BEGIN SOLUTION
# Réponse écart 0.0029 : c'est très faible
# si on trace les courbes avec Ktheo et Kopt, elles sont très proches.
# On est dans les incertitudes de mesures de cette expérience où il y a des frottements et nos mesures
# des positions restent approximatives.
### END SOLUTION
assert(xtest.size==9)
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif7',['plt.plot(','plt.legend(','plt.xlabel','plt.ylabel']))
11.2.8. Méthode alternative avec une régression linéaire#
On souhaite réutiliser les développements faits lors des précédents TP (anomalie de température sur le climat) sur la méthode de regression linéaire pour minimiser l’erreur au sens des moindres carrés afin de faire passer une droite dans une série des points de mesure.
Pour cela on transforme le problème en effectuant un changement de variable, pour se ramener à un problème de droite des moindres carrés.
En posant \(tsqr = t^2\), on note que la loi recherchée s’écrit maintenant : \(x = A*tsqr\).
Lisser les points expérimentaux avec une droite des moindres carrés: $\( y = a1*tsqr + a0 \)$
En déduire une nouvelle estimation de K dans la variable
Kmcavec une précision de 2 chiffres après la virguleTracez les points expérimentaux de la bille blanche en fonction de tsqr, ainsi que le lissage
Comparez le résultat avec le résultat précédent.
tsqr = None
a1 = 0
a0 = 0
Kmc = 0
### BEGIN SOLUTION
# tracer
# On retrouve une valeur proche de Kopt mais un peu moins bonne que la méthode précédente.
# La méthode de la regression linéaire est plus directe
# que les essais successifs précédents mais elle n'améliore pas la précision. Cela est dû au fait
# qu'il y a deux paramètres a0 et a1. Il faudrait réécrire une régression avec un seul paramètre.
### END SOLUTION
assert(Kmc*100 == int(Kmc*100))
assert(np.abs(Kmc-Kopt)<2.e-2)
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif8',['plt.plot(','plt.legend(','plt.xlabel','plt.ylabel']))
11.3. Étude des trajectoires et des vitesses moyennes des boules blanche, rouge et jaune.#
11.3.1. Relevé des trajectoires#
La fonction
np.load(nom_fichier)permet de relire des tableaux numpy qui ont été sauvegardés dans les fichiers CourbeBlanche.npy, CourbeRouge.npy et CourbeJaune.npy associés aux coordonnées des tracés blanc, rouge et jaune sur l’image (coordonnées en pixel).pour vérifier les mesures, superposez les différentes courbes sur l’image
brachistochroneSolo.pngen utilisant la fonctionplt.imshowcomme au début.
trajectBlanche = np.load('CourbeBlanche.npy')
trajectRouge = np.load('CourbeRouge.npy')
trajectJaune = np.load('CourbeJaune.npy')
### BEGIN SOLUTION
### END SOLUTION
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif9',['plt.imshow(','plt.plot(']))
11.3.2. transformation des mesures#
En plaçant le centre \(O\) d’un système cartésien \((0,\vec{x},\vec{y})\) au point de départ des trajectoires, effectuez le changement de repère nécessaire et tracez dans une nouvelle figure les courbes \(y(x)\) représentant chaque trajectoire avec \(x\) et \(y\) en mètres.
### BEGIN SOLUTION
### END SOLUTION
assert(test_code('TP_mesures_brachistochrone.ipynb','cell-verif10',['plt.legend(','plt.plot(','plt.xlabel']))
11.3.3. Calcul de la longueur de chaque tracé#
A partir des relevés des coordonnées des tracés, calculez une valeur approchée de la longueur en mètre de chaque tracé (blanc, rouge, jaune). On mettra les trois longueurs dans un tableau longueurs.
longueurs = None
### BEGIN SOLUTION
# Calcul des longueurs des trajectoires
### END SOLUTION
assert((longueurs.size == 3) and (np.all(longueurs>0.5)))
assert(np.abs(np.sum(longueurs) - 3.1784422339726355 ) < 1.e-4)
11.3.4. Calcul de la vitesse moyenne de chaque boulle#
Le première image est à \(t=0s\). Les boules blanche, rouge et jaune arrivent respectivement à la 649e, 521e, 577e image.
Calculez la vitesse moyenne de chaque boule dans un tableau vit_moy.
Concluez.
vit_moy = None
### BEGIN SOLUTION
# calcul des vitesses moyennes.
### END SOLUTION
assert((vit_moy.size == 3) and (np.all(vit_moy>1.0)))
assert(np.abs(np.sum(vit_moy) - 5.1859795687125025) < 1.e-4)
11.4. Compte rendu#
Ecrire votre analyse et votre conclusion dans le compte rendu en insistant sur
Description de la méthode d’analyse
Résultat de l’analyse
Conclusion
Le compte rendu est à écrire dans le fichier CompteRendu.md
Génération de la version HTML du Compte Rendu (avec mise en page)
Exécution de la commande ci-dessous pour générer le fichier html
Visualisation du Compte Rendu (version html)
Cliquez sur le lien suivant après exécution de la commande ci-dessous
Cliquez sur le bouton mise à jour du navigateur pour mettre à jour la page web
# génération de la version html du CR
!genereTPhtml CompteRendu
# test sur les commentaires (a executer)
assert(test_markdown('CompteRendu.md',None,minm=200,maxe=0.25))
11.5. FIN du TP#
