2. Saut à l’élastique: Bungee Jumping#

(C) Wikipedia
%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
2.1. Modélisation#
Phase 1: chute libre
Phase 2: oscillation élastique
modèle pendule élastique
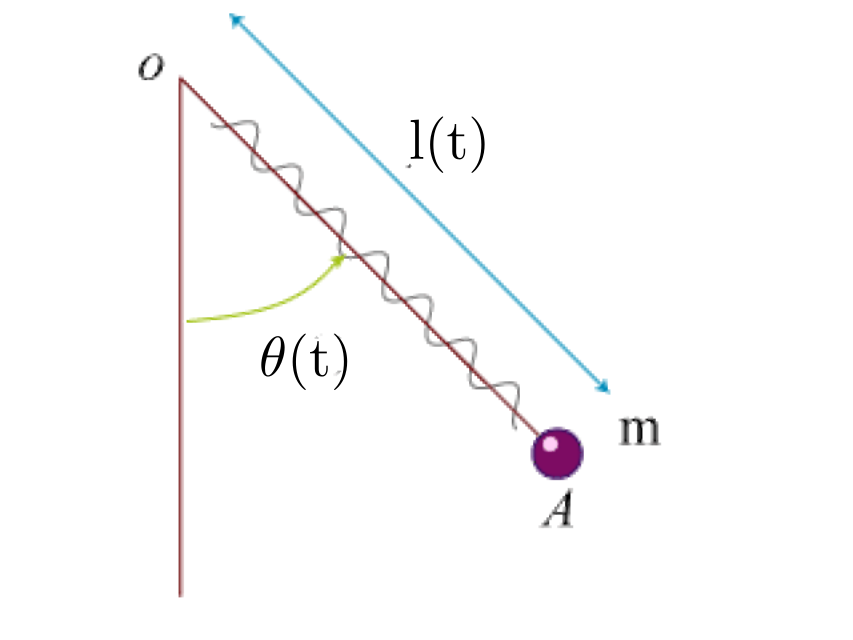
Un pendule élastique est constitué d’une tige mince de poids négligeable sur laquelle s’enroule un ressort. A l’extrémité du ressort est accrochée une masselotte considérée comme “ponctuelle”.
2.1.1. Phase d’analyse#
Quelles sont les questions à se poser !
2.1.2. Questions#
Quels sont les degrés de liberté du système ?
Quels sont les paramètres du système ?
Comment obtenir les équations du mouvement (PFD et bilan des forces) ?
2.1.3. degrés de liberté#
système à 2 degrés de liberté (mouvement plan) (position de A)
choix des ddl:
angle \(\theta(t)\) du pendule
allongement \(r(t)\) du ressort
\[ l(t) = l_0 + r(t) \]
2.1.4. paramètres#
\(g\) , \(l_0\), \(k\), \(m\)
et \(T_{max}\)
2.1.5. Bilan des forces#
poids \(\vec{P} = -mg \vec{e}_y\) suivant la verticale \(\vec{e}_y\)
tension du ressort \(\vec{T} = -k r \vec{e}_n\) suivant l’axe de la tige \(\vec{e}_n\)
Principe fondamentale de la dynamique $\(\vec{P} + \vec{T} = m \vec{\gamma}\)$
\(\leadsto\) 2 équations pour 2 inconnues
2.2. Mise en équation#
utilisation du calcul formel
définition des ddl (dynamicsymbols)
définition des parametres (symbols)
définition des repères (ReferenceFrame) et des position (Point)
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
m,g,k,l0 = sp.symbols('m g k l_0')
t = sp.symbols("t")
theta,r = dynamicsymbols('theta r')
# Repere et points
O = Point('O')
R0 = ReferenceFrame("R_0")
R1 = ReferenceFrame("R_1")
R1.orient(R0,'Axis',[theta,R0.z])
A = Point('A')
A.set_pos(O,-(l0+r)*R1.y)
# vitesse
O.set_vel(R0,0)
# calcul acceleration du pendule
display("V(A)/R0=",A.vel(R0).simplify())
MA = m*A.acc(R0).simplify()
display("m*Acc(A)/R0=",MA)
'V(A)/R0='
'm*Acc(A)/R0='
# bilan des forces
P = -m*g*R0.y
T = k*r*R1.y
F = (P+T).express(R1).simplify()
display("Forces=",F)
'Forces='
eq1 = (MA-F).dot(R1.x).simplify().expand()
eq2 = (MA-F).dot(R1.y).simplify().expand()
display("eq1=",eq1)
display("eq2=",eq2)
'eq1='
'eq2='
2.2.1. paramétrage des équations#
2 paramètres \(\omega_1\) et \(\alpha\)
x = dynamicsymbols('x')
omega1,alpha = sp.symbols("omega_1 alpha")
rel12 = {r : l0*x, l0:g/omega1**2,m:k*alpha/omega1**2}
eq11 = (eq1.subs(rel12).simplify()*omega1**4/(k*g*alpha)).expand()
display("eq1",eq11)
eq22 = (eq2.subs(rel12).simplify()*omega1**4/(k*g*alpha)).expand()
display("eq2",eq22)
'eq1'
'eq2'
2.2.2. Validation cas limites#
pendule simple \(x\approx cste=\alpha\) 1ddl \(\theta(t)\)
\[ (1+\alpha)\ddot{\theta} + \omega_1^2 \theta = 0 \]ressort simple \(\theta \approx 0\) 1 ddl \(x(t)\)
\[ \ddot{x} + \omega_2^2 (x - \alpha) = 0 \]
2.2.3. linéarisation: système en petites oscillations#
\(\theta \ll 1\) et \(x-\alpha \ll 1\)$
display(eq11)
eq11.subs({sp.sin(theta):theta,x.diff(t):0,x:alpha})
display(eq22)
eq22.subs({sp.cos(theta):1,theta.diff(t)**2:0})
2.2.4. Propriétés du système#
Système mécanique conservatif
énergie cinétique \(E_c = \frac{1}{2} m v^2\)
énergie potentielle \(Ep_1 = m g y\) et \(Ep_2 = \frac{1}{2} k r^2\)
Expression en fonction des paramètres
adimensionnalisation des équations par \(ml_0^2\)
\(E_c = \frac{1}{2} \left(((1+x)\dot{\theta})^2 + (\dot{x})^2\right)\)
\(Ep_1 = -\omega_1^2 (1+x) \cos\theta\) et \(Ep_2 = \frac{1}{2} \omega_2^2 x^2\)
2.3. Simulation numérique#
Transformation en ODE d’ordre 1
display(eq11)
f1 = (theta.diff(t,2)*(1+x)-eq11).simplify()/(1+x)
display("Eq1",sp.Eq(theta.diff(t,2),f1))
F1 = sp.lambdify([omega1,alpha,theta,x,theta.diff(t),x.diff(t)],f1,'numpy')
'Eq1'
display(eq22)
f2 = x.diff(t,2)+eq22
display("Eq2",sp.Eq(x.diff(t,2),f2))
F2 = sp.lambdify([omega1,alpha,theta,x,theta.diff(t),x.diff(t)],f2,'numpy')
'Eq2'
def Smb(Y,t):
"""Calcul smbd EDO dy/dt = F(Y,t)"""
global Omega1, Alpha
dYdt = np.array([Y[2], Y[3],
F1(Omega1,Alpha,Y[0],Y[1],Y[2],Y[3]),
F2(Omega1,Alpha,Y[0],Y[1],Y[2],Y[3])])
return dYdt
from scipy.integrate import odeint
def Solution(Y0,Tmax,N):
"""Calcul solution avec une CI Y0 sur un temps Tmax en N points"""
global Omega1, Omega2, Alpha
print("Solution pour omega1={} omega2={} alpha={}".format(Omega1,Omega2,Alpha))
TT = np.linspace(0,Tmax,N)
sol = odeint(Smb, Y0, TT)
THETA = sol[:,0]
R = sol[:,1]
# coordonnees
X = (1+R)*np.sin(THETA)
Y = -(1+R)*np.cos(THETA)
# module vitesse
V2 = ((1+R)*sol[:,2])**2 + sol[:,3]**2
EC = 0.5*V2
EP1 = Omega1**2*(Y+1)
EP2 = 0.5*Omega2**2*R**2
plt.figure(figsize=(16,8))
plt.subplot(1,3,1)
plt.plot(X,Y)
plt.plot(X[0],Y[0],'*r')
plt.axis('equal')
plt.title("Trajectoire")
plt.subplot(1,3,2)
plt.plot(TT,R,label="$r(t)$")
plt.plot(TT,THETA,label="$\\theta(t)$")
plt.title("Degré de liberté")
plt.xlabel('t')
plt.legend()
plt.subplot(1,3,3)
plt.plot(TT,EC,label="$E_c$")
plt.plot(TT,EP1,label="$Ep_1$")
plt.plot(TT,EP2,label="$Ep_2$")
plt.plot(TT,EC+EP1+EP2,label="$E_t$")
plt.title("Bilan d'énérgie")
plt.xlabel('t')
plt.legend()
plt.show()
return
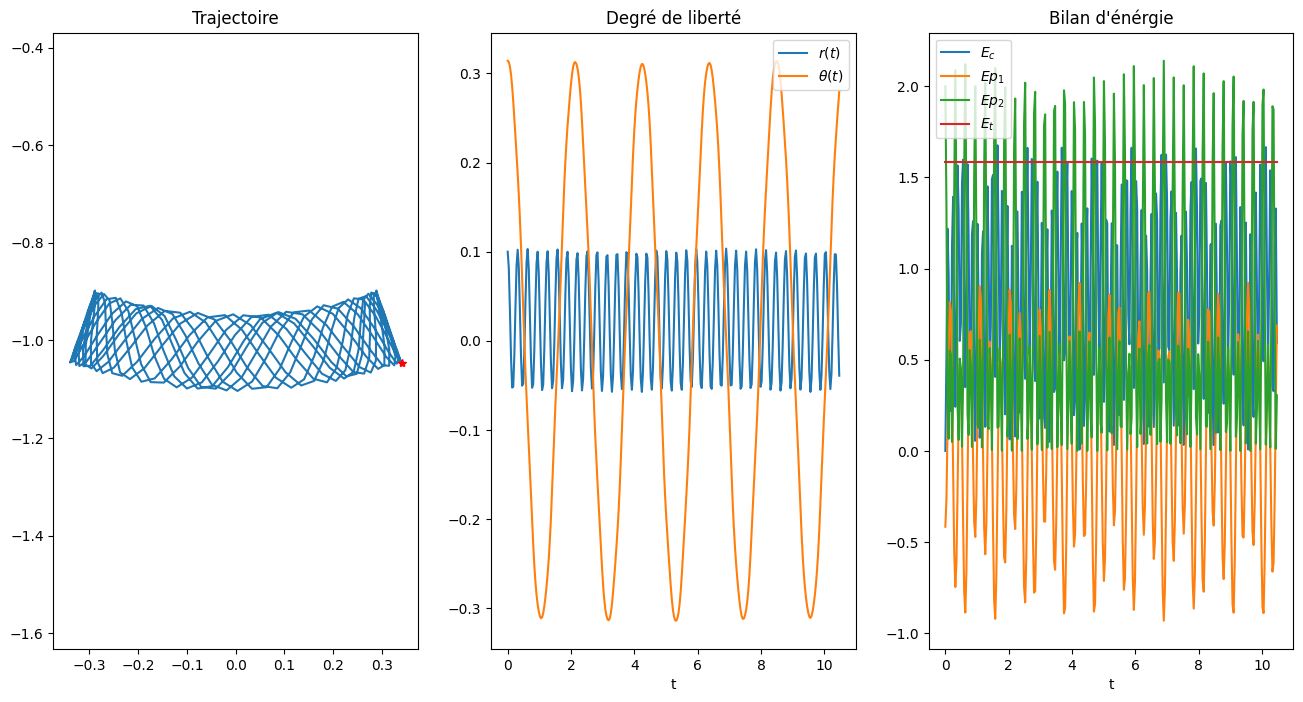
2.3.1. cas petites oscillations#
Omega1 = 3.0
Omega2 = 20.0
Alpha = Omega1**2/Omega2**2
Y0 = [np.pi/10, 0.1, 0., 0.]
Solution(Y0,5*2*np.pi/Omega1,300)
Solution pour omega1=3.0 omega2=20.0 alpha=0.0225
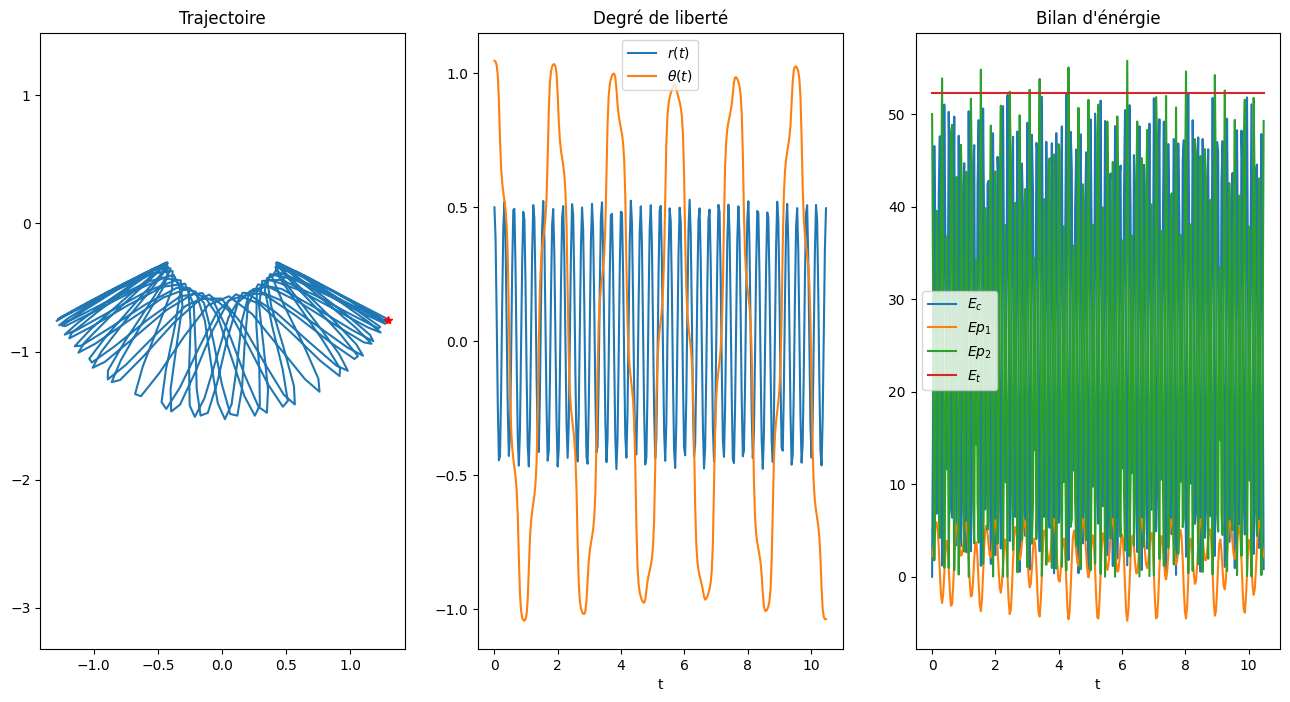
2.3.2. cas grandes oscillations#
Y0 = [np.pi/2, 0.5, 0., 0.]
Y0 = [np.pi/3, 0.5, 0., 0.]
Solution(Y0,5*2*np.pi/Omega1,300)
Solution pour omega1=3.0 omega2=20.0 alpha=0.0225
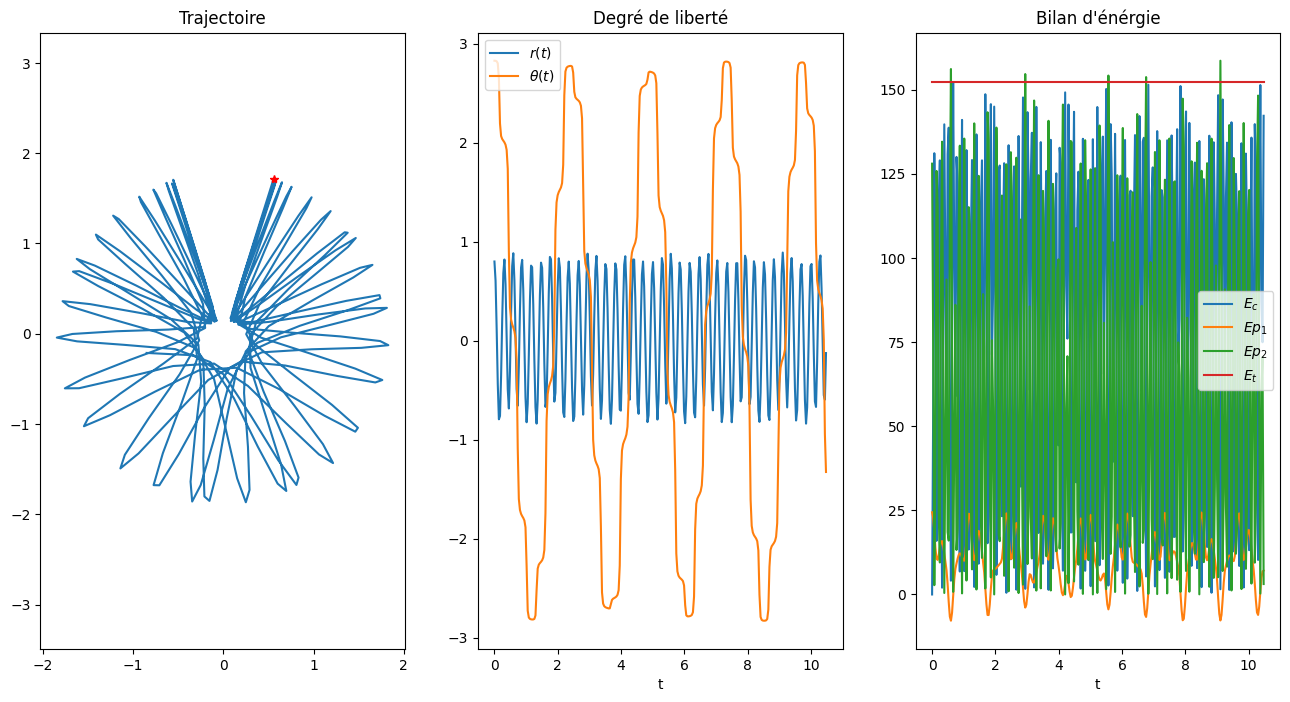
Y0 = [0.9*np.pi, 0.8, 0., 0.]
Solution(Y0,5*2*np.pi/Omega1,300)
Solution pour omega1=3.0 omega2=20.0 alpha=0.0225
2.4. Application saut élastique#
paramètres:
poids m=60 kg
corde élastique l0=30m avec un allongement d’une fois sa longueur à vide
phase 1: transfert énérgie potentiel en énergie cinétique
conditions initiales:
saut vertical: \(\theta = 0 , r = 0\) et \(\dot{\theta} = 0, \dot{r} = V_0\)
avec un angle: \(\theta = \theta_0 , r = 0\) et \(\dot{\theta} = 0, \dot{r} = V_0\)
calcul du coefficient k:
transformation énergie cinétique en potentiel élastique (alongement de \(2 l_0\))
\[ \frac{1}{2} k l_0^2 = \frac{1}{2} m v_0^2 \]d’où
\[ k = \frac{mg}{l_0}\]
# parametres
G = 9.81
L0 = 30.0
M = 60.
V0 = np.sqrt(2*G*L0)
K = M*G/(L0)
Omega1 = np.sqrt(G/L0)
Omega2 = np.sqrt(K/M)
Alpha = Omega1**2/Omega2**2
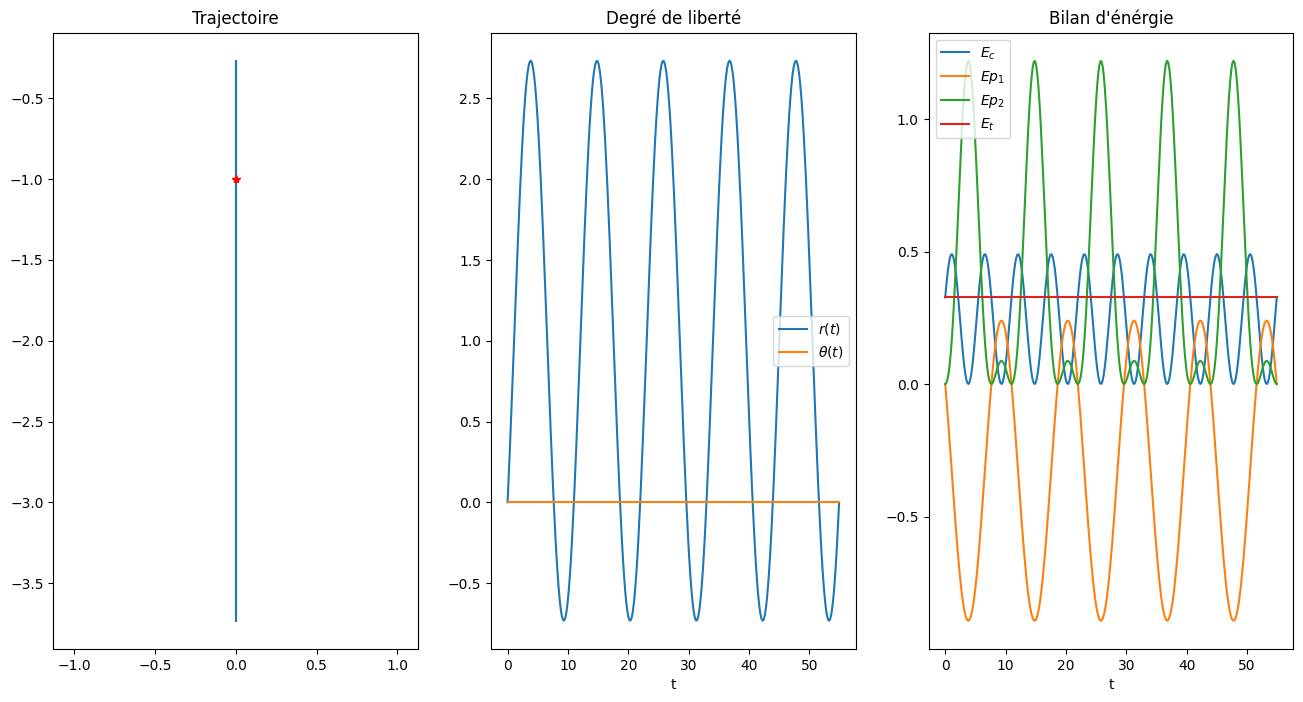
2.4.1. saut vertical#
Y0 = [0.0, 0.0, 0., V0/L0]
Solution(Y0,5*2*np.pi/Omega1,300)
Solution pour omega1=0.5718391382198319 omega2=0.5718391382198319 alpha=1.0
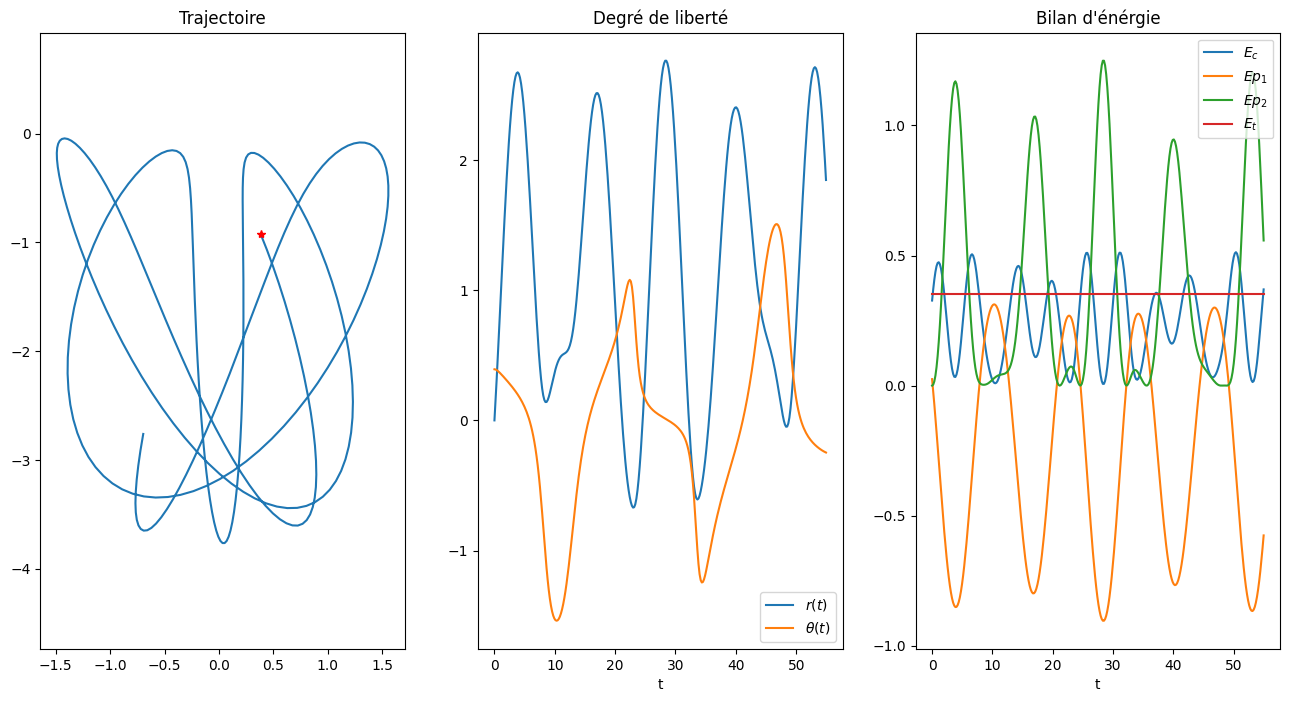
2.4.2. saut incliné#
Y0 = [np.pi/8, 0.0, 0., V0/L0]
Solution(Y0,5*2*np.pi/Omega1,300)
Solution pour omega1=0.5718391382198319 omega2=0.5718391382198319 alpha=1.0
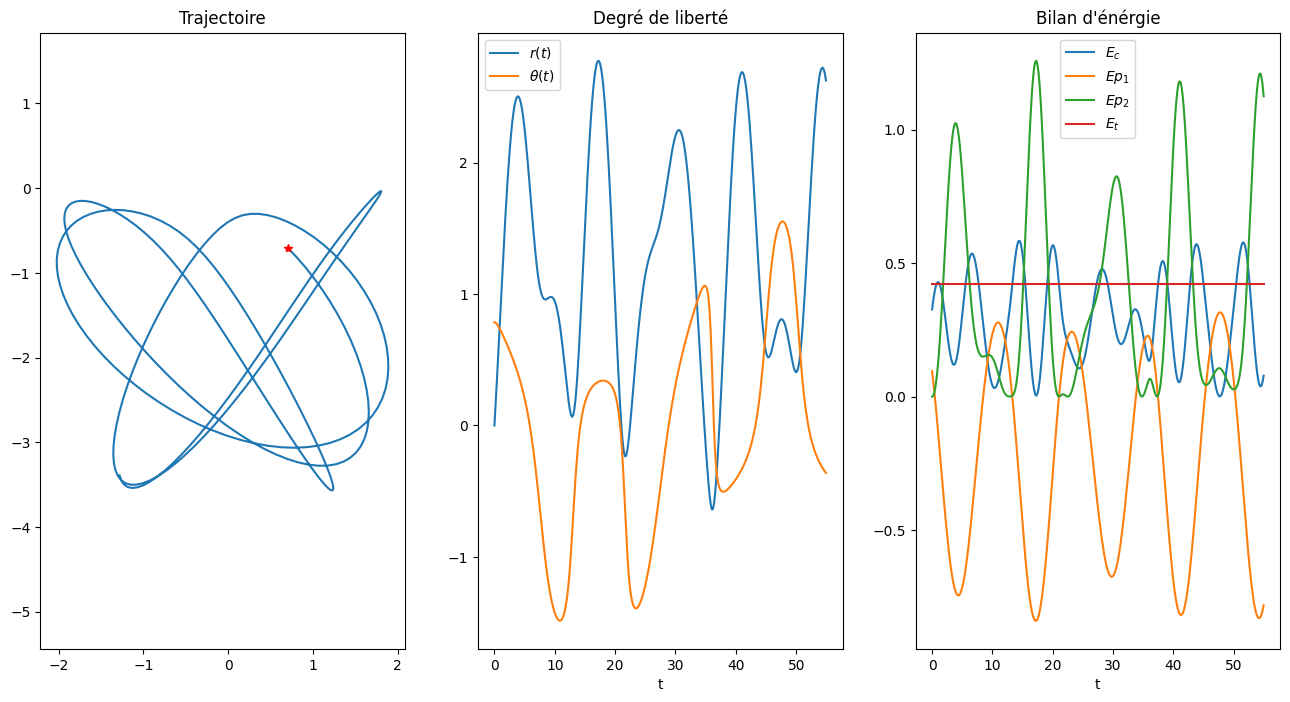
Y0 = [np.pi/4, 0.0, 0., V0/L0]
Solution(Y0,5*2*np.pi/Omega1,300)
Solution pour omega1=0.5718391382198319 omega2=0.5718391382198319 alpha=1.0
2.5. Annexe I: intégration en coordonnées cartésienne (y,z)#
Omega2 = Omega1/np.sqrt(Alpha)
print(Omega1,Omega2,Alpha)
L0 = 1.0
G = 9.0
def SmbYZ(Y,t):
R = np.sqrt(Y[0]**2+Y[1]**2)
C = Omega2**2*(R-L0)/R
return np.array([Y[2],Y[3],-C*Y[0], -C*Y[1] - G])
0.5718391382198319 0.5718391382198319 1.0
Y0 = np.array([0.34,-1.046,0,0])
TT = np.linspace(0,5*2*np.pi/Omega1,500)
print(SmbYZ(Y0,0))
sol = odeint(SmbYZ, Y0, TT)
XX = sol[:,0]
YY = sol[:,1]
[ 0. 0. -0.01009541 -8.96894177]
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(XX[0],YY[0],'*r')
plt.plot(XX,YY)
plt.title("trajectoire")
plt.axis('equal')
plt.subplot(1,2,2)
plt.plot(TT,XX,label="x(t)")
plt.plot(TT,YY,label="y(t)")
plt.xlabel('t')
plt.legend()
<matplotlib.legend.Legend at 0x7f823e3587c0>
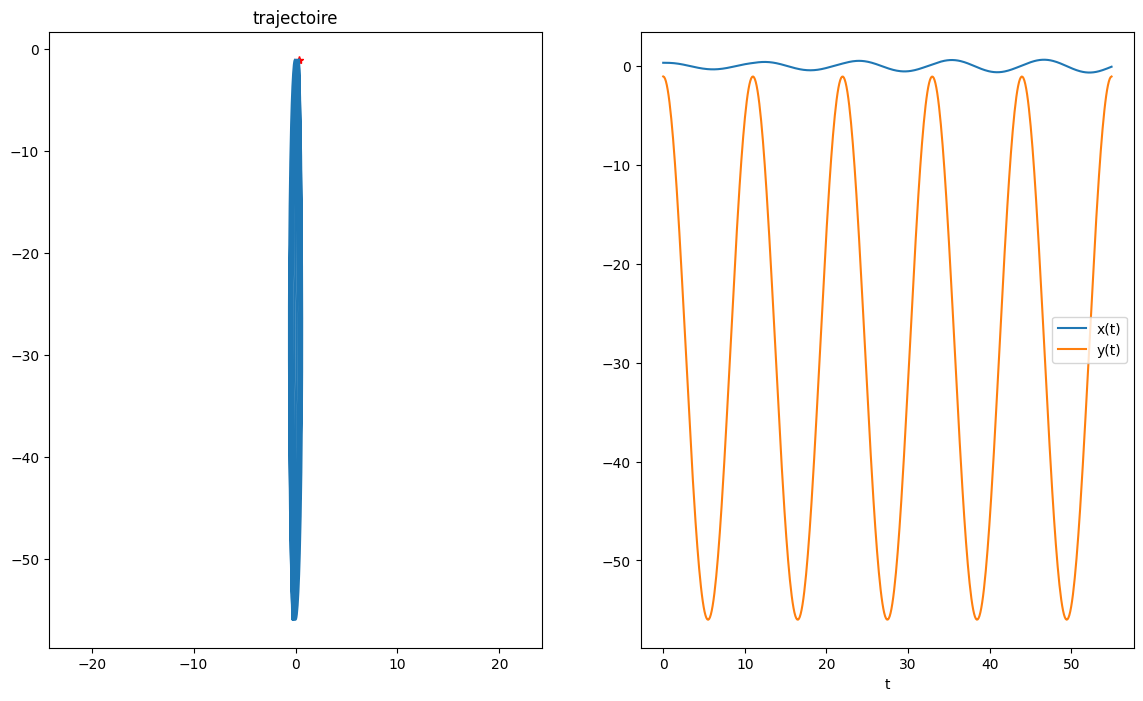
On retrouve bien la même trajectoire, mais l’analyse est moins simple (comparer les courbes \(x(t),y(t)\) avec \(\theta(t),r(t)\)
