4.1. Rappel d’analyse

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

%matplotlib inline
import numpy as np
import sympy as sp
from sympy.plotting import plot
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display

4.1.1. Objectifs

Dans de nombreux problèmes de mécanique, on se ramène à devoir étudier des fonctions.

Par exemple, supposons que pour étudier la trajectoire d’un point P, on trouve une vitesse \(\vec{V}(t)=f(t) \vec{e}\) où \(\vec{e}\) est un vecteur de direction fixe.

Les questions qui se posent sont:

1. Sur cette trajectoire, quelle sont les phases d’accélération et de décélération ?

2. Quelle est la vitesse maximum et minimum ?

3. Quelle est la distance parcourue en fonction du temps ?

Toutes ces informations nous sont fournis par les outils d’analyse mathématique, qui est le domaine des mathématiques qui traite des propriétés des fonctions. Pour étudier les variations d’une fonction, on calcule son tableau de variation en calculant sa dérivée \(\gamma\) et en étudiant son signe.

\[ \gamma = \frac{d f}{dt} \mbox{ accélération dans la direction }\vec{e}\]

La distance parcourue \(L(T)\) dans la direction \(\vec{e}\) pendant un temps \(T\) corresponds à l’intégrale de la fonction:

\[ L(T) = \int_0^T f(t)\;dt\]

L’analyse mathématique offre les outils pour

1. étudier les fonctions,

2. calculer la dérivée d’une fonction,

3. calculer l’intégrale d’une fonction.

Note

On rappelle ci-dessous les éléments essentiels d’analyse mathématique à connaître et à savoir utiliser.

4.1.2. Etude de fonction

• fonction d’une variable \(F(x)\)

• caractéristiques ?

  • signe

  • croissance ou décroissance

  • continuité et limite $\( \lim_{x\rightarrow a} F(x) \)$

• tableau de variation

  • analyse grossière: tracé de la fonction sur un intervalle (à choisir)

  • analyse fine: calcul de la dérivée et étude de son signe

4.1.2.1. Exemple

• étude de la fonction \(y = \tanh x\)

• tableau de variation

• étude de \(\tanh{(ax + b)}\)

x = sp.symbols('x')
plot(sp.tanh(x),(x,-5,5),title="fonction y=tanh(x)",ylabel="y");

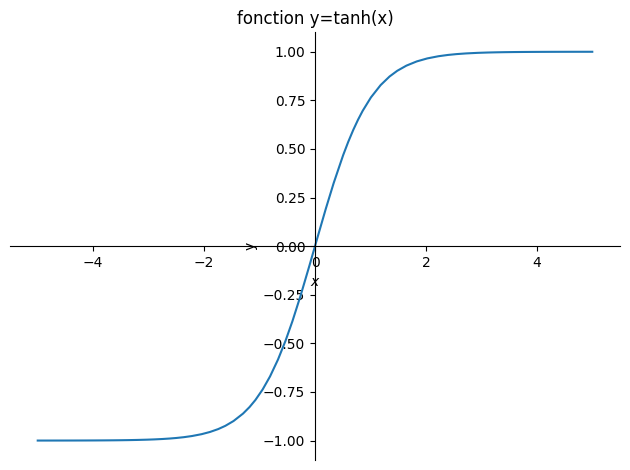
tableau de variation de \(f(x)=\tanh(x)\) qui est une fonction croissante

\[\frac{d }{dx}\tanh(x) = 1 - \tanh^2(x)\]

\[\begin{split} \begin{array}{|c|ccccr|} \hline x & -\infty & & 0 & & +\infty \\ \hline f'(x) & 0 & + & 1 & + & 0 \\ \hline & & & & & +1 \\ % ligne des valeurs "max" f(x) & & & \nearrow & & \\ % flèches & -1 & & & & \\ % ligne des valeurs "min" \hline \end{array} \end{split}\]

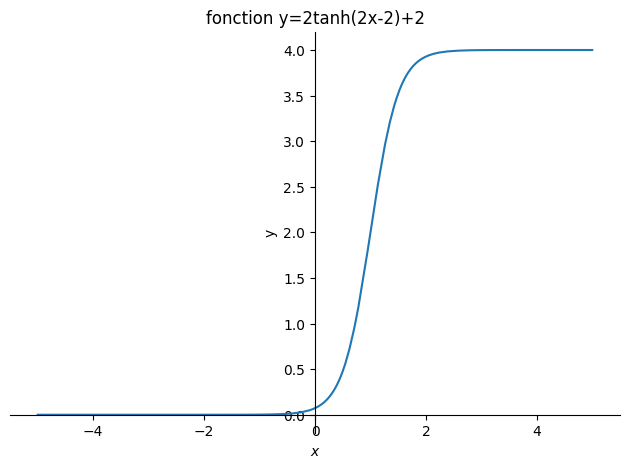
généralisation étude de \(f(x)=2\tanh(2x-2)+2\)

\[\frac{d }{dx} f(x) = 4 - 4\tanh^2(2x-2)\]

\[\begin{split} \begin{array}{|c|ccccr|} \hline x & -\infty & & 0 & & +\infty \\ \hline f'(x) & 0 & + & 4 & + & 0 \\ \hline & & & & & +4 \\ % ligne des valeurs "max" f(x) & & & \nearrow & & \\ % flèches & 0 & & & & \\ % ligne des valeurs "min" \hline \end{array} \end{split}\]

sp.plot(2*sp.tanh(2*x-2)+2,(x,-5,5),title="fonction y=2tanh(2x-2)+2",ylabel="y");

4.1.3. Dérivées

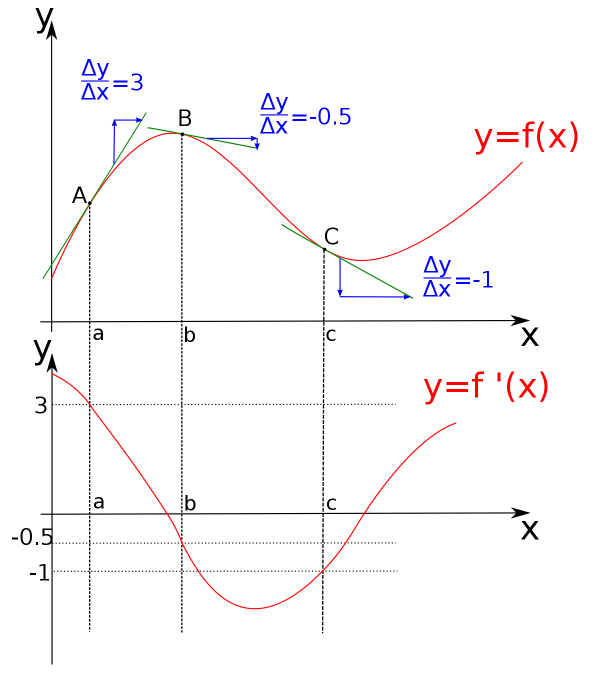
• Définition de \(f'(x)\)

\[ f'(a) = \frac{df}{dx}(x=a) = \lim_{h\rightarrow 0} \frac{f(a+h)-f(a)}{h} \]

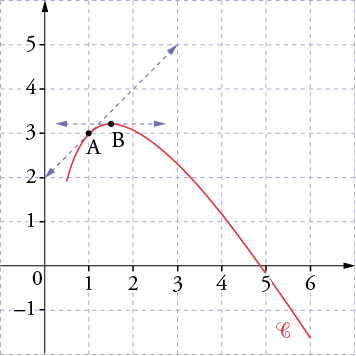
• Interprétation

  • tangente à la courbe pente \(f'(a)\)

  • équation de la tangente en \((x_0,y_0)\)

  \[ y - y_0 = f'(x_0) (x-x_0)\]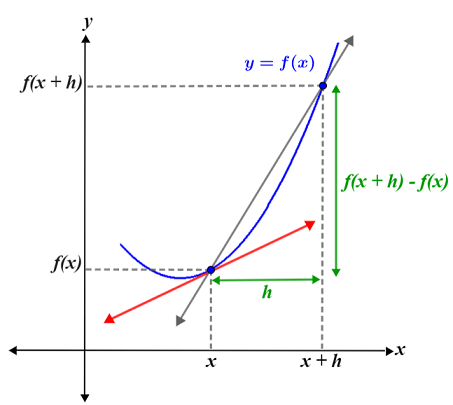

  

• Exemple:

\[ \tanh x = \frac{\sinh x}{\cosh x} = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]

• calcul de la dérivée

\[\frac{d }{dx}\tanh(x) = 1 - \tanh^2(x)\]

• étude du signe et des limites

• tableau de variation

# solution: calcul avec sympy
y = sp.tanh(x)
y.diff(x)

\[\displaystyle 1 - \tanh^{2}{\left(x \right)}\]

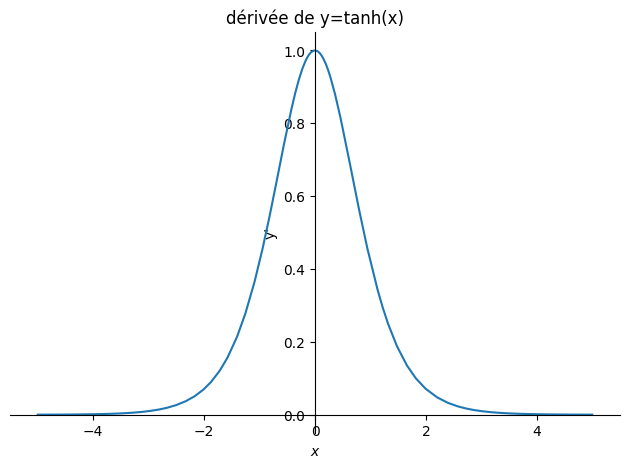
plot(sp.tanh(x).diff(x),(x,-5,5),title="dérivée de y=tanh(x)",ylabel="y'");

4.1.3.1. formules à connaître (par coeur)

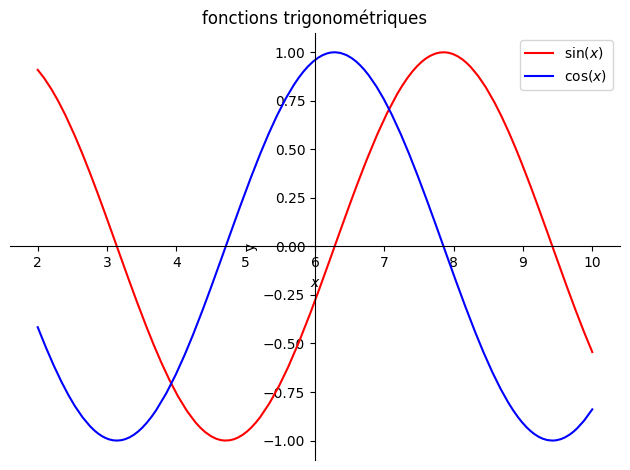
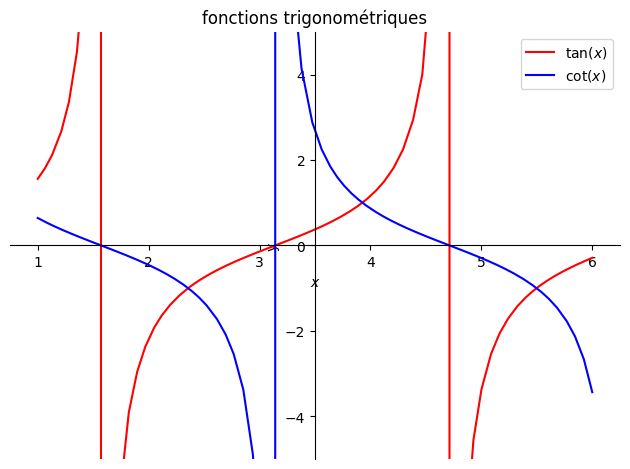
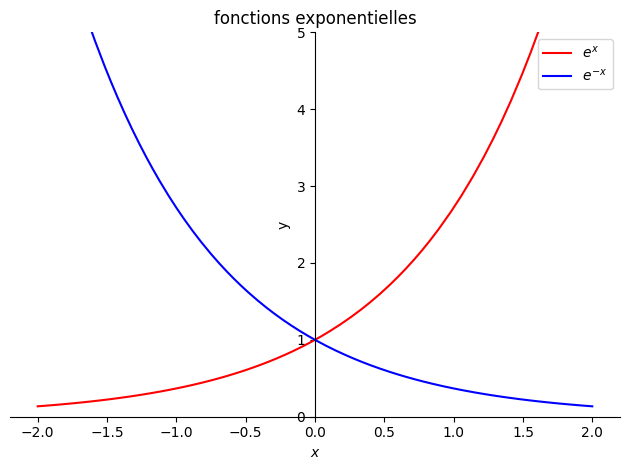
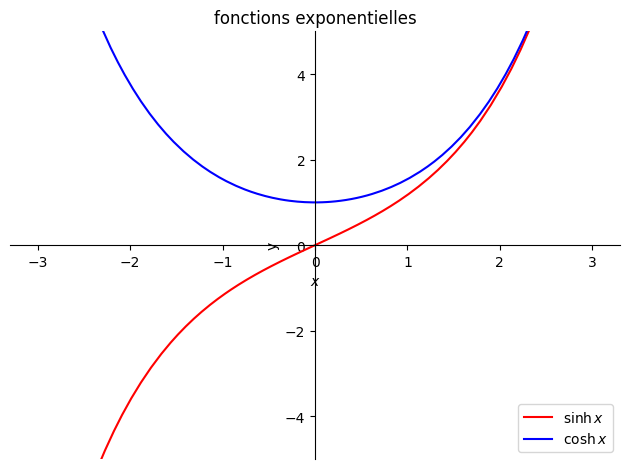
• allure des fonctions polynôme degré 2, degré 3, sinus, cosinus, tangente, exp, sinh, cosh, tanh

dérivées de fonctions usuelles

• dérivées de fonction polynomiales, trigonométriques et exponentielles

\[\begin{split} \begin{eqnarray} \frac{d}{dx} x^p &=& p x^{p-1}\\ \frac{d}{dx} \sin(x) &=& \cos(x)\\ \frac{d}{dx} \cos(x) &=& - \sin(x)\\ \frac{d}{dx} e^x &=& e^x\\ \frac{d}{dx} e^{\alpha x} &=& \alpha e^{\alpha x}\\ \frac{d}{dx} \cos(\omega x) &=& - \omega \sin(\omega x)\\ \end{eqnarray} \end{split}\]

régies de dérivation

• règles de dérivation (somme, produit, dérivation composée)

\[\begin{split} \begin{eqnarray} \frac{d}{dx} (\alpha f(x) + \beta g(x)) &=& \alpha\frac{df}{dx}+ \beta\frac{dg}{dx}\\ \frac{d}{dx} (f(x)g(x)) &=& g(x)\frac{df}{dx} + f(x) \frac{dg}{dx}\\ \frac{d}{dx} (f(g(x)) &=& \frac{dg}{dx} \frac{df}{dx}(g(x))\\ \end{eqnarray} \end{split}\]

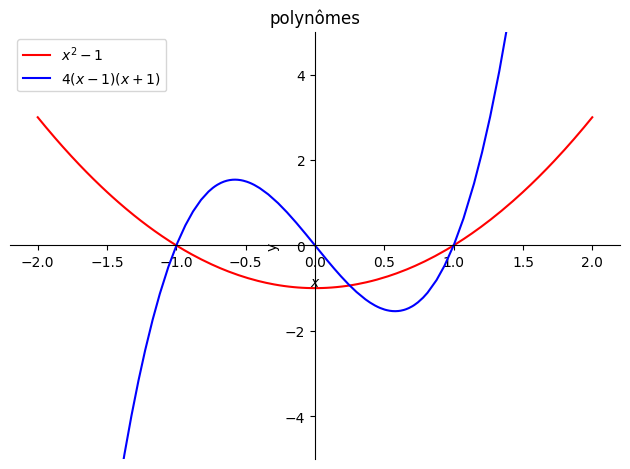
p1=plot(x**2-1,(x,-2,2),ylim=(-5,5),line_color='r',ylabel="y",title="polynômes",
        legend=True,show=False)
p1[0].label="$x^2-1$"
p2=plot(4*(x-1)*(x+1)*x,(x,-2,2),line_color='b',legend=True,show=False)
p2[0].label="$4(x-1)(x+1)$"
p1.append(p2[0])
p1.show()

p1=plot(sp.sin(x),(x,2,10),line_color='r',ylabel="y",title="fonctions trigonométriques",legend=True,show=False)
p2=plot(sp.cos(x),(x,2,10),line_color='b',legend=True,show=False)
p1[0].label="$\sin(x)$"
p2[0].label="$\cos(x)$"
p1.append(p2[0])
p1.show()

p1=plot(sp.tan(x),(x,1,6),ylim=(-5,5),line_color='r',ylabel="y",title="fonctions trigonométriques",legend=True,show=False)
p2=plot(sp.cot(x),(x,1,6),ylim=(-5,5),line_color='b',legend=True,show=False)
p1[0].label="$\\tan(x)$"
p2[0].label="$\cot(x)$"
p1.append(p2[0])
p1.show()

p1=plot(sp.exp(x),(x,-2,2),ylim=(0,5),line_color='r',ylabel="y",title="fonctions exponentielles",legend=True,show=False)
p2=plot(sp.exp(-x),(x,-2,2),ylim=(0,5),line_color='b',legend=True,show=False)
p1[0].label="$e^x$"
p2[0].label="$e^{-x}$"
p1.append(p2[0])
p1.show()

p1=plot(sp.sinh(x),(x,-3,3),ylim=(-5,5),line_color='r',ylabel="y",title="fonctions exponentielles",legend=True,show=False)
p2=plot(sp.cosh(x),(x,-3,3),ylim=(-5,5),line_color='b',legend=True,show=False)
p1[0].label="$\sinh x$"
p2[0].label="$\cosh x$"
p1.append(p2[0])
p1.show()

4.1.4. Intégrales

L’intégrale d’une fonction f(x) s’interprète geometriquement comme l’aire sous la courbe

\[ S = \int_a^b f(x)\,dx \]

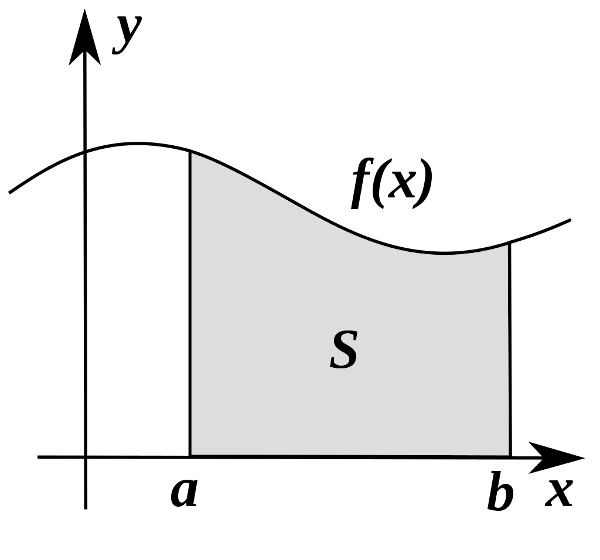
4.1.4.1. définition

• intégrale au sens de Rieman:

\[ \int_a^b f(x)\,dx = \lim_{N\rightarrow\infty} \sum_{i=1}^N \frac{f(x_i) +f(x_i-h)}{2} h \mbox{ avec } x_i = a + ih \mbox{ et } h = \frac{b-a}{N}\]

• primitive \(F(x)\) de \(f(x)\)

  • si \(f(x) = F'(x)\) alors:

\[ \int_a^b f(x)\,dx = F(b) - F(a)\]

• valeur moyenne \(\overline{f} \) de \(f(x)\)

  \[\overline{f} = \frac{1}{b-a} \int_a^b f(x)\,dx\]

4.1.4.2. propriétés

Les affirmations suivantes sont-elles vraies ou fausses (et pourquoi)

1. la valeur de \(S = \int_a^b f(x)\,dx \) est toujours positive car c’est une surface

2. si \(\int_a^b f(x)\,dx = 0 \) alors \(f(x)\) est nulle puisque sa moyenne est nulle

Les affirmations suivantes sont-elles vraies ou fausses (et pourquoi)

1. la valeur de \(S = \int_a^b f(x)\,dx \) est toujours positive si \(f(x)\ge 0\)

2. si \(\int_a^b f(x)\,dx = 0 \) et \(f(x)\ge 0\) alors \(f(x)\) est nulle (p.p.)

4.1.4.3. formules à connaître (par coeur)

intégrales de fonctions usuelles

• intégrales des fonction polynomiales, trigonométriques et exponentielles

(4.1)\[\begin{eqnarray} \int x^p dx &=& \frac{x^{p+1}}{p+1} \mbox{ si } p \neq -1\\ \int \sin(x) dx &=& - \cos(x)\\ \int \cos(x) dx &=& \sin(x)\\ \int e^x dx &=& e^x\\ \int e^{\alpha x} dx &=& \frac{e^{\alpha x}}{\alpha}\\ \int \cos(\omega x) dx &=& \frac{\sin(\omega x)}{\omega}\\ \end{eqnarray}\]

règles d’intégration

règles d’intégration (somme, produit, changement de variables)

\[\begin{split} \begin{eqnarray} \int_a^b{(\alpha f(x) + \beta g(x)) \, dx} &=& \alpha\int_a^b{f(x)\,dx}+ \beta\int_a^b{g(x)\,dx}\\ \int_a^b{f(x)\,dx} &=& \int_{\xi(a)}^{\xi(b)}{f(\xi)\frac{dx}{d\xi}\,d\xi} \end{eqnarray} \end{split}\]

4.1.5. Approximations numériques

4.1.5.1. dérivée \(f'(a)=\frac{df}{dx}(x=a)\)

on choisit une valeur \(h\) petite ( p.e. \(h\approx 0.01\))

• approximation simple

\[ f'(a) \approx \frac{f(a+h) - f(a)}{h} \]

• approximation plus précise (centrée)

\[ f'(a) \approx \frac{f(a+h) - f(a-h)}{2h} \]

4.1.5.2. intégrale \(\int_a^b f(x) dx\)

on choisit un nombre de points \(N\) , d’où \(h = \frac{b-a}{N}\) et \(x_i = a + ih \)

• méthode des trapèzes

\[ \int_a^b f(x) dx = \sum_{i=1}^N \frac{f(x_i) +f(x_i-h)}{2} h \]

4.1.5.3. propriétés des approximations

cours de L3 « Calcul scientifique »

• précision de l’approximation

• ordre

• convergence