TP EDO: système masse ressort avec amortissement

9. TP EDO: système masse ressort avec amortissement#

Marc BUFFAT, dpt mécanique, Université Lyon 1

inspiré par le cours « Engineering Computations » du Pr L. Barba (Washington Univ.)

../../../../_images/damped-spring1.png

Attention il faut exécuter la cellule vide suivante !!

# bibliothéque
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
plt.rc('font', family='serif', size='14')
# parametres
from validation.validation import info_etudiant, bib_validation, test_function
from validation.valide_markdown import test_markdown, test_code
from IPython.display import display, Markdown, clear_output
bib_validation('cours','MGC2028L')
from Oscillation import test1,test2,test3,test4,test5,test6
notebook_name = "TP_vibration.ipynb"
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_  = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Etudiant** {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_mcl_ = ['énergie','cinétique','potentielle','période','erreur','amortie','oscillation', 'forcage']
_omega0 = np.random.randint(1,10)
# systeme
_m  = np.round(0.1+2*np.random.rand(),2)
_k  = _m*_omega0**2
_b  = np.round(0.1+0.5*np.random.rand(),2)
# CI
_x0 = np.round(0.5*(2*np.random.rand()-1),2)
_v0 = 0.
# forcage
_omega  = _omega0/2.
_A = np.round(_x0*_omega0**2*0.25*(0.1+np.random.rand()),2)
if (np.abs(_A)<0.5): _A = 0.5
#
printmd("**parametres:** masse m={}, raid.k={}, amort.b={} Forcage: omega={},A={} CdtsInit: x0={},v0={}".format(_m,_k,_b,_omega,_A,_x0, _v0))

9.1. Le système masse-ressort#

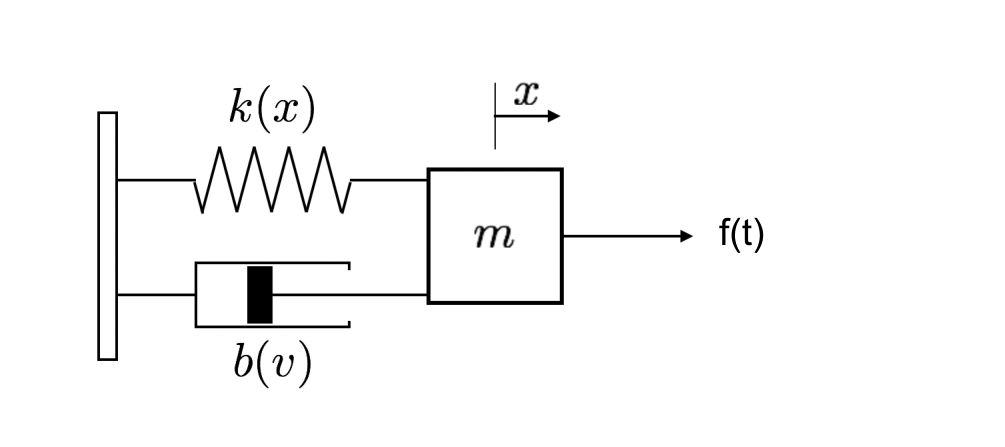
Le système oscillant mécanique le plus simple est une masse \( m \) attachée à un ressort, sans frottement. Nous avons discuté de ce système dans la leçon précédente. En général, cependant, ces systèmes sont soumis à des frottements représentés par un amortisseur mécanique et à une force motrice d’excitation. De plus, la force de rappel du ressort pourrait être une fonction non linéaire de la position.

../../../../_images/damped-spring1.png

9.1.1. système masse ressort avec amortissement et forçage#

La loi de Newton appliquée au système masse-ressort général (entraîné, amorti) s’écrit:

(9.1)#\[\begin{equation} \mbox{Trouvez x(t) tq. : } m \ddot{x} = m\,f(t) -mb\,\dot{x} - k\,x \end{equation}\]

où

  • \(x(t)\) représente l’allongement du ressort

  • \(f(t)\) représente une force extérieure de forçage par unité de masse,

  • \(b\dot{x}\) une force d’amortissement par unité de masse,

  • \(k\,x(t)\) une force de rappel .

En divisant par \(m\) et en notant \(\omega^2 = \frac{k}{m}\), ce système est équivalent à

(9.2)#\[\begin{equation} \mbox{Trouvez x(t) tq. : } \ddot{x} = f(t) -b\,\dot{x} - \omega_0^2\,x \end{equation}\]

que l’on peut l’écrire comme un système de deux équations différentielles d’ordre 1,

(9.3)#\[\begin{eqnarray} \dot{x} &=& v, \nonumber\\ \dot{v} &=& F(t) - \omega_0^2 x - bv \end{eqnarray}\]

En notant \(Y(t)\) le vecteur d’état

(9.4)#\[\begin{equation} \mathbf{Y} = \begin{bmatrix} x \\ v \end{bmatrix} \end{equation}\]

la forme vectorielle du système précédent s’écrit alors:

(9.5)#\[\begin{equation} \dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y},t) \mbox{ avec } \mathbf{F}(\mathbf{Y},t) = \begin{bmatrix} v \\ f(t) - \omega_0^2\,x - b\,v \end{bmatrix}. \end{equation}\]

Dans ce système général, la variable temps apparaître explicitement dans le second membre de droite, via la fonction de forçage \(f(t)\), donc le second membre \(F\) dépend explicitement de \(Y(t)\) et de \(t\).

9.2. Système masse ressort sans forcage \(F(t)=0\)#

Pour résoudre le problème, nous allons en écrire une fonction MasseRessortAmorti pour décrire notre modèle.

On définira en particulier les variables omega0 et ben fonction des paramètres du problème. Ces 2 variables seront définit comme des variables globales dans la fonction, ce qui permet de les définir en dehors de la fonction et de les utiliser dans la fonction dans le but de permettre une modification facile en dehors de la fonction. Ecrire cette fonction python dans la cellule ci-dessous

       def MasseRessortAmorti(Y, temps):
       
        '''
        calcul le second membre du système masse ressort avec amortissement
        Arguments
        ---------   
        Y :     vecteur d'etat [x, v]
        temps:  instant t de calcul

        Retour 
        -------
        derivs:  derivée du vecteur d'etat = F(Y,t)
        '''
        global omega0, b

Vérifier dans la cellule suivante en appelant la fonction avec une valeur Y0 t.q. y=0.1, v=0. et t=0. On mettra le résultat dans la variable F0. On affichera ensuite la valeur de F0 et son type pour vérifier

printmd("**parametres:** masse m={} [kg], raid. k={} [kg/s^2], amort. b={} [s^-1] CdtsInit: x0={} [m],v0={} [m/s]".format(_m,_k,_b,_x0, _v0))

# definition de la fonction MasseRessortAmorti(Y, temps)
# et des variables globales
b = 0
omega0 = 0
### BEGIN SOLUTION
### END SOLUTION

# Verification: appel de la fonction pour y=0.1, v=0. et t=0
F0 = None
Y0 = None
### BEGIN SOLUTION
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.2.1. Méthode numérique#

Pour calculer la solution numérique du système d’EDO

\[\dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y}(t),t)\]

on utilise la méthode de Runge Kutta, mais sous forme matricielle puisque la solution est un vecteur (de dimension 2) et non plus un scalaire.

Pour cela on se fixe le temps de simulation \(t_max\) et un nombre de pas en temps \(n\), ce qui permet de définir un vecteur T contenant les temps où on calcule numériquement la solution, et qui est donnée par :

\[ T_i = i\Delta t \mbox{ pour } i=0,n \]

On calcule ensuite la solution numérique sous forme d’une matrice Y de dimension (n+1,2) qui pour chaque ligne i contient la valeur numérique de \(\mathbf{Y}(T_i)\) au temps \(T_i\)

\[ Y[i,:] \approx \mathbf{Y}(t=T[i]) \mbox{ pour } i=1,n \mbox{ et } Y[0,:] = \mathbf{Y}_0\]

On calcule la valeur de ce vecteur solution \(Y[i,:]\) avec la méthode numérique de Runge Kutta 2, qui s’écrit sous forme matricielle (en notant \(t_m = \frac{t_i + t_{i-1}}{2}\))

(9.6)#\[\begin{align} \mathbf{Y}_m & = \mathbf{Y}[i-1,:] + \frac{\Delta t}{2} \mathbf{F}(\mathbf{Y}[i-1,:],t_{i-1}) \\ \mathbf{Y}[i,:] & = \mathbf{Y}[i-1,:] + \Delta t \,\, \mathbf{F}(\mathbf{Y}_m,t_m). \end{align}\]

9.2.2. Fonction RK2#

Pour appliquer cette méthode, on demande d’écrire une fonction RK2(F,T,Y0) qui prend pour arguments les paramètres du problème : la fonction second membre F de l’EDO, le vecteur T des pas en temps et la condition initiale Y0.

Cette fonction calcule la valeur numérique de la solution Y (qui est une matrice). En utilisant une boucle itérative, on calcule chaque ligne de Y en utilisant la méthode précédente. A la fin, la fonction renvoie la valeur Y.

## Fonction RK2(F,T,Y0)
## BEGIN SOLUTION
## END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

Vérification

En utilisant comme vecteur T=[0,0.1,0.2] , utilisez la fonction précédente pour calculer Y en ces instants. On vérifiera le type et la taille de Y.

# Verification
T = np.array([0,0.1,0.2])
Y0 = None
Y = None
### BEGIN SOLUTION
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.2.3. Paramètres du problème#

On définit une période periode à partir de la pulsation propre du système \(\omega_0\).

On fait le calcul sur 10 périodes avec 100 pas en temps par période.

  1. En déduire la valeur du temps final dans tfin

  2. définit la dimension N du tableau T et mettre dans T les valeurs des temps \(t_i = i\,dt\) où on calcule la solution avec linspace .

  3. Définir la valeur initiale x0 et v0

  4. Afficher la periode et le pas en temps et la CI pour vérifier

# 
x0 = 0
v0 = 0
tfin = 0
N  = 0
T  = None
periode = 0
### BEGIN SOLUTION
# time array
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.2.4. Calcul de la solution#

  1. Définir dans Y0 le vecteur condition initiale

  2. Calculer la solution numérique sol_num1 en appelant la fonction RK2

  3. Vérifier en affichant la taille et le type de la solution numérique

  4. Tracer l’évolution en temps de la position et de la vitesse

# iteration en temps
sol_num1 = None
Y0 = None
### BEGIN SOLUTION
# solution par la méthode de Runge Kutta 2
# plot solution 
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.2.5. Propriétés de conservation#

Le système masse-ressort sans amortissement possède une propriété importante d’un point de vue mécanique: c’est un système mécanique conservatif, c.a.d., l’énergie totale du système se conserve au cours du temps. L’énergie totale par unité de masse est la somme de l’énergie cinétique par unité de masse: \(Ec = \frac{1}{2} v^2\) et de l’énergie potentielle par unité de masse: \(U = \frac{1}{2} \omega_0^2 x^2\) associée à la force de rappel: \( -k x = \frac{d U}{dx}\). On se propose d’étudier cette propriété dans le cas de notre système masse-ressort amorti.

  1. calculer l’énergie cinétique et potentielle du système dans Ec1 et Up1

  2. tracer leur évolution en fonction du temps

  3. commentez le résultat (as-t-on conservation de l’énergie dans notre cas ?)

On notera E0 l’énergie par unité de masse du système à l’instant initial.

Ec1 = None
Up1 = None
E0 = 0.0
### BEGIN SOLUTION
# calcul de l'energie par unité de masse pour la méthode Runge Kutta 2
# energie initiale
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.2.6. Commentaires#

Ecrire dans le compte rendu les commentaires sur les résultats et les courbes obtenues, en particulier sur:

- la forme de la solution numérique
- l'évolution de l'énergie cinétique et potentielle
- la période, l'amplitude (constante ou amortie) de la solution
- la vérification de propriétés de conservation
- l'évolution en temps de la solution et de l'énergie

attention à l’orthographe (sinon vous perdez des points)

9.3. Etude du cas avec forçage sinusoidal#

Supposons maintenant qu’une force externe de la forme \(f(t) = A \sin(\omega t)\) excite le système. C’est une situation typique dans les systèmes mécaniques. Regardons à quoi ressemble le système dans ce cas.

printmd("**parametres:** masse m={}, raid. k={}, amort. b={} Forcage: omega={},A={} CdtsInit: x0={},v0={}".format(_m,_k,_b,_omega,_A,_x0, _v0))

9.3.1. Définition du modèle avec forçage f(t)#

On considère le cas d’un forçage sinusoidal \(f(t) = A \sin(\omega t)\).

écrivons la fonction second membre MasseRessortForcage pour le système masse-ressort forcé (avec amortissement). On utilisera deux variables globales A et omega supplémentaires dans la fonction pour définir ce forçage.

La forme vectorielle de l’équation différentielle s’écrit alors:

(9.7)#\[\begin{equation} \dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y},t) \mbox{ avec } \mathbf{F}(\mathbf{Y},t) = \begin{bmatrix} v \\ f(t) - \omega_0^2\,x - b\,v \end{bmatrix}. \end{equation}\]

On vérifiera ensuite la fonction en l’appelant avec un vecteur d’état \(Y_0\) correspondant à \(x=0.1\) et \(v=0.0\) à l’instant \(t=0\)

Ecrire la fonction MasseRessortForcage qui implémente cette fonction \(\mathbf{Y}\)

 def MasseRessortForcage(Y, temps):
     global b,omega0,A,omega

L’amplitude A et \(\omega\) sont définit comme des paramètres globaux comme b et \(\omega0\)

Vérifier dans la cellule suivante en appelant la fonction avec une valeur Y0 t.q. y=0.1, v=0. et t=0. On mettra le résultat dans la variable F0. On affichera ensuite la valeur de F0 et son type pour vérifier

# valeurs des parametres A et omega
A = 0
omega = 0
### BEGIN SOLUTION
### END SOLUTION

# Verification: appel de la fonction pour y=1, v=2. et t=0
F0 = None
Y0 = None
### BEGIN SOLUTION
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.3.2. Simulation#

Calculer la solution numérique dans la cellule de code ci-dessous avec les mêmes paramètres du modèle que nous avons utilisés pour le système amorti sans forçage. La valeur de la CI a mettre dans Y0 sera la même que précédemment.

La solution sera calculer dans un vecteur sol_num2

On calculera aussi l’énergie cinétique et potentielle dans Ec2 et Up2

Y0 = None
sol_num2 = None
Ec2 = None
Up2 = None
### BEGIN SOLUTION
# calcul de l'energie par unité de masse 
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.3.3. Tracé de la solution#

dans la cellule suivante tracer l’évolution de x , de l’énergie cinétique, potentielle et totale en fonction du temps. On commentera le résultat dans le compte rendu.

# tracer de la solution et de l'énergie
### BEGIN SOLUTION
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.3.4. Commentaires#

Dans le compte rendu, on commentera ces 2 courbes, en particulier sur:

- la forme de la solution numérique
- l'évolution de l'énergie cinétique et potentielle
- l'évolution en temps de la solution et de l'énergie
- la période et l'amplitude du système et son évolution au cours du temps

On pourra comparer avec le cas sans forcage, expérimenter avec différentes valeurs des paramètres du forçage F et sur le temps total de simulation.

9.4. Etude de la résonance#

Un comportement intéressant se produit lorsque l’amortissement est suffisamment faible et que la fréquence du forçage coïncide avec la fréquence propre du système masse-ressort, \( \omega_0=\sqrt{k / m}\):

Refaire le calcul de la solution avec un forçage \(f(t)=A\sin(\omega t)\) tq \(\omega = \omega_0\).

  1. redéfinir les parametres omega et A du forcage

  2. calculer la solution sol_num3

  3. On calculera aussi l’énergie cinétique et potentielle dans Ec3 et Up3

printmd("**parametres:** masse m={},raid. k={},amort. b={} Forcage: A={} CdtsInit: x0={},v0={}".format(_m,_k,_b,_A,_x0, _v0))

omega = 0
A = 0
Y0 = None
sol_num3 = None
Ec3 = None
Up3 = None
### BEGIN SOLUTION
# calcul de l'energie par unité de masse 
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.4.1. Tracé de la solution#

dans la cellule suivante tracer l’évolution de x , de l’énergie cinétique, potentielle et totale en fonction du temps. On commentera le résultat dans le compte rendu.

# tracer de la solution et de l'énergie
### BEGIN SOLUTION
#plt.title("Energie Ec et Up");
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.4.2. Commentaires#

Dans le compte rendu, commenter le résultat, en particulier:

- la forme de la solution numérique
- l'évolution de l'énergie cinétique et potentielle
- l'évolution en temps de la solution et de l'énergie
- la période du système et son évolution au cours du temps

9.5. Solutions dans le plan de phase#

Le système masse-ressort, comme vous le voyez, peut se comporter de différentes manières. Si le ressort est linéaire et qu’il n’y a pas d’amortissement ou de forçage (comme dans la leçon précédente), le mouvement est périodique. Si nous ajoutons de l’amortissement, le mouvement oscillatoire décroît avec le temps. Avec le forçage, le mouvement peut être un peu plus compliqué et parfois présenter une résonance.

Chacun de ces types de mouvement est représenté par des solutions correspondantes au système différentiel, dictées par les paramètres du modèle et les conditions initiales.

Comment avoir une idée de tous les types de solutions à un système différentiel? Une méthode puissante pour ce faire est d’utiliser le plan de phase.

Un système de deux équations différentielles du premier ordre:

(9.8)#\[\begin{eqnarray} \dot{x}(t) &=& f(x, y) \\ \dot{y}(t) &=& g(x, y) \end{eqnarray}\]

avec un vecteur d’état

(9.9)#\[\begin{equation} \mathbf{Y} = \begin{bmatrix} x \\ y \end{bmatrix}, \end{equation}\]

est appelé un système autonome planaire: planaire, car le vecteur d’état a deux composantes; et autonome (auto-génératrice), car la variable de temps n’apparaît pas explicitement sur le côté droit (qui ne s’appliquerait pas au système masse-ressort entraîné).

Pour les conditions initiales \(\mathbf{Y} _0 = (x_0, y_0) \), le système a une solution unique \( \mathbf{Y} (t) = \left (x (t), y (t) \right) \) . Cette solution peut être représentée par une courbe plane sur le plan \( xy \) le plan de phase et est appelée une trajectoire du système.

Pour les différentes solutions numériques, tracer la trajectoire dans l’espace des phases?

# tracer dans l'espace des phases
### BEGIN SOLUTION
### END SOLUTION

# ne rien écrire dans cette cellule
### BEGIN HIDDEN TESTS
### END HIDDEN TESTS

9.5.1. Commentaires#

Ecrire vos commentaires dans le compte-rendu

  • que peut on dire de ces trajectoires ?

  • vers quel état évolue le système ?

9.6. Compte rendu#

Ecrire votre analyse et voss conclusion dans le compte rendu en insistant sur

  1. Description de la méthode d’analyse

  2. Résultat de l’analyse

  3. Conclusion

Le compte rendu est à écrire dans le fichier CompteRendu.md

  1. Génération de la version HTML du Compte Rendu (avec mise en page)

  • Exécution de la commande ci-dessous pour générer le fichier html

  1. Visualisation du Compte Rendu (version html)

  • Cliquez sur le lien suivant après exécution de la commande ci-dessous

  • Cliquez sur le bouton mise à jour du navigateur pour mettre à jour la page web

9.7. Analyse#

9.7.1. cas sans forcage#

9.7.2. cas avec forcage#

9.7.3. résonnance#

# génération de la version html du CR
!genereTPhtml CompteRendu

9.8. FIN du TP#

# version
from platform import python_version,uname,platform
print("Systeme       :",uname())
print("OS            :",platform())
print("version python:",python_version())
print("version numpy :",np.__version__)
Contenu