12. Outils de calcul formel en Mécanique#
Marc BUFFAT département mécanique, université Lyon 1
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
#
from IPython.display import display, Markdown, clear_output
def printmd(string):
display(Markdown(string))
from metakernel import register_ipython_magics
register_ipython_magics()
12.1. Question préliminaire#
%activity /usr/local/commun/ACTIVITY/IntroPython/questionBrachistochrone
12.2. Objectifs#
Utilisation d’un outil de calcul formel et de calcul numérique pour étudier la cinématique et la dynamique des solides, permettant de résoudre complètement le problème.
application de la démarche du cours
mise en équation en utilisant du calcul formel pour faciliter les calculs analytiques (changement de repère, projection, composition des mouvements,..)
résolution numérique des équations pour obtenir la solution
ATTENTION ces outils ne sont pas une boite noir pour résoudre automatiquement les problèmes. Il faut comprendre la démarche pour pouvoir les utiliser à bon escient.
12.3. Outils de calcul symbolique et numérique#
Utilisation du langage de programmation Python et des notebooks Ipython
Utilisation de bibliothèques python spécialisées en calcul numérique:
numpy (documentation) (numerical python): pour le calcul numérique avec une manipulation simple de vecteurs et matrices (à la matlab)
matplotlib: pour le tracer de courbes en 2D
k3D : pour la visualisation 3D de trajectoires
import numpy as np import k3d import matplotlib.pyplot as plt
et en calcul symbolique:
sympy symbolic python
sympy.physics.vector bibliothèque sympy pour manipuler des vecteurs et des repères en 3D (projection, dérivation ..)
sympy.physics.classical mechanics bibliothèque sympy pour l’étude de la cinématique et dynamique des solides
import sympy as sp from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, RigidBody from sympy.physics.vector import dot
Attention en général quand on utilise une fonction d’une bibliothéque python, on préfixe en général la fonction par le nom (simplifié) de la bibliothéque
np.cos(..)
sp.symbols(..)
Régles
on évite de mélanger calcul numérique et calcul symbolique
pour le calcul symbolique on utilise exclusivement
sympy(sp) pour les fonctions mathématiquessp.cos sp.sin s.tan ….
pour le calcul numérique on utilise exclusivement
numpy(np) pour les fonctions mathématiquesnp.cos np.sin …
12.4. Paramètres, Point et Référentiel#
sous python, on va utiliser des variables (objets) dont la valeur est un symbole. Lors de la création, on doit définir comment sera affiché le symbole en fournissant la chaîne de caractère qui sera affichée. Par défaut sympy reconnaît les lettres grecques( i.e. “alpha” sera affiché \(\alpha\)) et les indices (i.e. “X_A” sera affiché \(X_A\))
paramètres du problème
fonction sp.symbols() pour définit des variables symboliques
alpha,L = sp.symbols('alpha L')
degrés de liberté du problème
fonction dynamicsymbols pour définir un degré de liberté (fct de t)
xa, ya = dynamicsymbols('x_a y_a')
repère = base orthormée de \(\mathcal{R}^3\) pour définir des vecteurs (direction)
référentiel = un point + un repère pour définir la position de point ou de solide dans l’espace ainsi que de leur mouvement.
repère (frame)
fonction ReferenceFrame: definit un repère (base)
R1 = ReferenceFrame('R_1')ensuite on utilise les fonctions (méthodes) associées pour positionner le repère (rotation par rapport à un autre repère) (orient)
R1.orient(R0,'Axis',[psi, R0.z])
point
fonction Point: définit un point dans l’espace
A = Point('A')ensuite on utilise les fonctions (méthodes) associées pour positionner le point par rapport à un autre point: set_pos
pour positionner le point A: on écrit : \(\overrightarrow{OA} = r \overrightarrow{R_1.x}\)
A.set_pos(O,r*R1.x)
pour afficher la position / un autre point
A.pos_from(O)
on peut demander l’expression dans un repere R1
A.pos_from(O).express(R1)
12.5. Composition des mouvements#
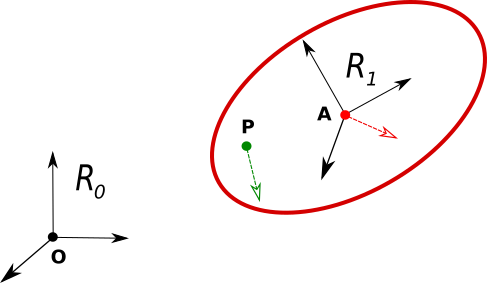Dans un référentiel fixe \(R_0\) d’origine O, on étudie la cinématique (mouvement) d’un solide S définit par un point A et un repère \(R_1\) lié à S.
On a s’intéresse à la cinématique d’un point P (observateur) dans \(R_1\) connaissant la cinématique de A en utilisant la composition des mouvements.
12.5.1. composition des vitesses \(V\)#
On veut calculer la vitesse en P connaissant la vitesse d’un autre point A. On distingue 2 cas:
Dans le cas général, on connait la vitesse du point P dans \(R_1\) et celle de A dans \(R_0\) ( 1 point theory: P et A n’appartiennent pas au même solide S)
A et P sont fixes dans \(R_1\) ( 2 points theory: A et P appartiennent au solide S) $\(\overrightarrow{V}^{\,R_0}_P = \overrightarrow{V}^{\,R_0}_A + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{AP}\)$
Les fonctions membres (méthodes) .v1pt_theory et .v2pt_theory de la classe Point font le calcul symbolique
# si P mobile dans R1, calcul V(P)/R0
P.v1pt_theory(A,R0,R1)
# et si P et A sont fixes dans R1
P.v2pt_theory(A,R0,R1)
12.5.2. composition des accélérations \(\gamma\)#
le point P est mobile dans \(R_1\) ( 1 point theory: A et P n’appartiennent pas au même solide S)
le point P est fixe dans \(R_1\) ( 2 points theory: A et P appartiennent au même solide S)
Les fonctions membres (méthodes) a1pt_theory et a2pt_theory de la classe Point font le calcul symbolique
# si P mobile dans R1
P.a1pt_theory(A,R0,R1)
# et si P et A sont fixes dans R1
P.a2pt_theory(A,R0,R1)
12.5.3. opération sur les vecteurs (et expression symbolique)#
dot produit scalaire \(\vec{A} . \vec{B}\)
A.dot(B)cross produit vectoriel \(\vec{A}\wedge\vec{B}\)
A.cross(B)express projection d’un vecteur dans un repère
A.express(R1)simplify simplification
A.simplify()subs substitution (argument dictionnaire (nom,valeur)) `A.subs({R:2})
diff(t,R1) dérivation d’un vecteur par rapport à t dans un repére R1
A.diff(t,R1)
12.6. Dynamique#
RigidBody() définit un solide à partir de sa masse M, de son centre de gravité G, d’un repère associé \(R_3\) et de sa matrice d’inertie IG en un point
inertia() calcul des matrices d’inertie
IG = inertia(R2,I2,I2,I1) solide = RigidBody('Solide',G,R3,M,(IG,G))
On utilise ensuite les fonctions membres (méthodes) pour calculer les quantités dynamique: - la quantité de mouvement linear_momentum, - le moment cinétique angular_momentum, - l’énergie cinétique kinetic_energy ….
12.7. Exemple 1: modélisation d’un solide en translation/rotation#
On veut modéliser un solide en translation dans le plan et en rotation autour de l’axe vertical (problème de la toupie).
Dans un repère fixe \((O,R_0)\), on étudie le mouvement d’un solide de masse M, de centre de gravité G (de coordonnées \(x_g,y_g,0\)). On note \(R_1\) le référentiel lié au solide dans lequel la matrice d’inertie \(I_G\) en G s’écrit: $\( I_G = \left[ \begin{matrix}I_1 & 0 & 0\\ 0 & I_2 & 0\\0 & 0 & I_3 \end{matrix} \right]\)\( Le référentiel \)R_1\( est obtenu à partir de \)R_0\( par une rotation d'angle \)\theta\( autour de \)R_0.z$.
On définit donc:
les paramêtres du problème \(M, I_1, I_2, I_3\)
les degrés de liberté: \(x_g, y_g, \theta\)
les points O et G
les repères \(R_0\) et \(R_1\)
la position du repère R1 par rapport à R0
la position de G par rapport à O
la vitesse de O / R0 et G /R1 (=0)
définition de la matrice d’inertie du solide en G dans R1: diagonale (I1,I2,I3)
inertia(R1,I1,I2,I3)
solide = centre G, refentiel R1 lié au solide, masse M et d’inertie IG / G
RigidBody(“nom”,G, R1, M, (IG,G))
# bibliothéques utilisées
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, RigidBody, inertia
# parametres et définition solide S
M, I1, I2, I3, t = sp.symbols('M I_1 I_2 I_3 t')
# degré de liberté (fct de t)
xg, yg, theta = dynamicsymbols('x_g y_g theta')
# repere fixe
O = Point('O')
R0 = ReferenceFrame('R_0')
# point et repère lié au solide (rotation /)
G = Point('G')
R1 = ReferenceFrame('R_1')
# position de G et R1 par rapport a O et R0
# calcul vitesse de G
# definition du solide S a partir des moments d'inerties
## BEGIN SOLUTION
G.set_pos(O, xg*R0.x + yg*R0.y)
R1.orient(R0,'Axis',[theta,R0.z])
# vitesse de O et G
O.set_vel(R0,0)
G.set_vel(R1,0)
# moment d'inertie dans R1 (axes principales d'inertie)
IG = inertia(R1,I1,I2,I3)
# solide S
S = RigidBody('S',G, R1, M, (IG,G))
## END SOLUTION
12.7.1. vitesse, quantité de mouvement, moment cinétique#
En utilisant les calculs précédents, calculez et afficher avec la fonction display()
calculer VG = dOG/dt par dérivation des composantes (utilisation de la méthode .diff(t))
en déduire la vitesse du point G dans R0 avec .set_vel(frame,VG)
afficher la vitesse de g avec la méthode .vit(frame) exprimée dans R1 avec .express(frame)
la quantité de mouvement de S dans R0 avec .linear_momentum(frame)
le moment cinétique de S en G dans R0 avec .angular_momentum(point,frame)
le moment cinétique de S en O dans R0 avec .angular_momentum(point,frame)
l’énergie cinétique de S .kinetic_energy(frame)
# propriété cinematique
VG = 0
## BEGIN SOLUTION
VG = G.pos_from(O).diff(t,R0)
display("VG=",VG)
G.set_vel(R0,VG)
display("VG=",G.vel(R0).express(R1))
display("Q=",S.linear_momentum(R0))
display("Sigma(G)=",S.angular_momentum(G,R0))
display("Sigma(O)=",S.angular_momentum(O,R0))
display("Ec=",S.kinetic_energy(R0))
## END SOLUTION
'VG='
'VG='
'Q='
'Sigma(G)='
'Sigma(O)='
'Ec='
print("VG=",VG)
assert( VG == G.vel(R0))
VG= Derivative(x_g(t), t)*R_0.x + Derivative(y_g(t), t)*R_0.y
12.7.2. composition des mouvements#
Soit P un point du solide S tel que $\( \vec{GP} = d \vec{R_1.x}\)$
définir le point P
calculer par composition des vitesses la vitesse de P avec la méthode
.v2pt_theory(point du solide,frame,frame du solide)
calcul OP et en déduire par dérivation temporelle VP, et simplifier avec .simplify()
comparer les 2 résultats
d = sp.symbols('d')
P = Point('P')
VP = 0
OP = 0
## BEGIN SOLUTION
P.set_pos(G,d*R1.x)
#P.set_vel(R1,0)
P.v2pt_theory(G, R0, R1)
display("V(P)=",P.vel(R0))
OP = P.pos_from(O)
VP = OP.diff(t,R0).simplify()
#VP = OP.diff(t,R0)
display("VP=",VP)
## END SOLUTION
'V(P)='
'VP='
display("VP=",VP,"V(P)=",P.vel(R0))
assert(VP == Point.vel(P,R0))
'VP='
'V(P)='
12.7.3. accélération#
calculer dans AP l’accélération de P par dérivation de VP avec .diff(t,repère)
simplifier avec .simplify()
calculer l’accélération de P avec la méthode .acc(repère)
# entrez vos calculs ici
AP = 0
## BEGIN SOLUTION
AP = VP.diff(t,R0).simplify()
#AP = VP.diff(t,R0)
display("AP=",AP)
display("A(P)=",P.acc(R0))
## END SOLUTION
'AP='
'A(P)='
display("AP=",AP,"A(P)=",P.acc(R0))
assert( AP == Point.acc(P,R0))
'AP='
'A(P)='
12.8. Conversion d’une expression symbolique en fonction numérique#
Objectif: utilisation du calcul symbolique pour faire de la simulation numérique
bibliothéque numpy (documentation)
bibliothéque matplotlib (documentation) pour le tracé de courbes
sp.lambdify() conversion expression symbolique en fonction python
soit u une expression symbolique fonction de plusieurs paramètres: A,omega, phi et t
on choisit le paramètre de la fonction, p.e t et on remplace tous les autres paramètres par des valeurs numériques avec une substitution
.subs()on convertit l’expression ainsi obtenue en fonction numpy de t
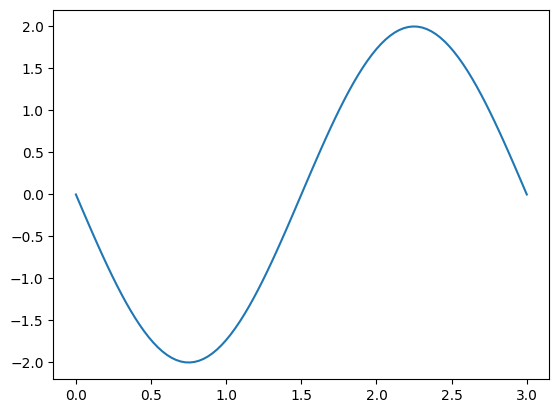
u = A*cos(omega*t+phi) us = u.subs([(A,2.0),(omega,2*np.pi/3.),(phi,np.pi/2)] U = sp.lambdify([t],us,'numpy') # utilisation de la fonction T = np.linspace(0,3,100) Y = U(T) plt.plot(T,Y)
entrez les instructions précédentes dans la cellule pour tester
# entrez vos instructions
A,omega,phi = sp.symbols('A omega phi')
u = A*sp.cos(omega*t+phi)
display("u=",u)
us = 0
## BEGIN SOLUTION
us = u.subs({A:2.0,omega:2*np.pi/3.,phi:np.pi/2})
display('us',us)
U = sp.lambdify([t],us,'numpy')
# utilisation de la fonction
T = np.linspace(0,3,100)
Y = U(T)
plt.plot(T,Y)
## END SOLUTION
'u='
'us'
[<matplotlib.lines.Line2D at 0x7f3d1835aef0>]
12.9. Exemple 2: application au mouvement d’une toupie#
Le solide S correspond à un disque plein de rayon \(𝑅=3\), de masse \(𝑀=2\). On considère un point P sur le disque distant de \(d=R\) de G. Le système S correspond donc à une toupie tournant autour de son axe z et se déplaçant dans le plan.
La matrice d’inertie vaut: $\( 𝐼_𝐺 = 𝑀𝑅^2 \begin{bmatrix} 1/4& 0& 0 \\ 0& 1/4 &0 \\ 0 & 0 &1/2 \end{bmatrix} \)$
On veut calculer la cinématique du solide S pour une trajectoire de G rectiligne et une rotation constante: $\( 𝑥_𝑔(𝑡) = 𝑡, 𝑦_𝑔(𝑡) = \frac{t}{2}, \theta(𝑡)=𝑡 \)$
Pour on utilisera la fonction .subs() avec comme argument une liste de substitution:
vals={nom1:exp1,nom2:exp2,..]
pour remplacer \(x_g,y_g\) et \(\theta\) et une autre liste pour les valeurs numériques
valnum={nom11:val1,nom22:val2,..]
En utilisant f=sp.lambdify([t],expres) on peut transformer une expression fonction de t expres en fonction Python f(t).
calculer les 2 fonctions Python
xP(t)etyP(t)donnant la position de P au cours du temps après subsitution des paramêtres. Il faut aussi utiliser la méthode.doit()pour forcer l’évaluation des expressions après substritution (par exemple pour calculer les dérivées).de même, calculer la fonction Python
eC(t)qui donne l’énergie cinetique de S au cours du tempsenfin, calculer la fonction python
sigmaG(t)qui donne la composante suivant \(R0.z\) du moment cinétique en G
Essayer avec plusieurs valeurs différentes du diamètre d de la toupie: d=1,2,3,5
# entrez vos calcul ici (on a d=R)
vals = {xg:t, yg:t/2, theta:t, I1:M*d**2/4, I2:M*d**2/4, I3:M*d**2/2}
valnum = {M:2, d:3}
xP = 0
yP = 0
eC = 0
sigmaG = 0
## BEGIN SOLUTION
xp = P.pos_from(O).express(R0).subs(vals).subs(valnum).dot(R0.x)
yp = P.pos_from(O).express(R0).subs(vals).subs(valnum).dot(R0.y)
xP = sp.lambdify([t],xp)
yP = sp.lambdify([t],yp)
# energie cinetique
ec = S.kinetic_energy(R0).subs(vals).subs(valnum).doit()
eC = sp.lambdify([t],ec)
# moment cinetique en G suivant Z
sigmag = S.angular_momentum(G,R0).subs(vals).subs(valnum).dot(R0.z).doit()
sigmaG = sp.lambdify([t],sigmag)
## END SOLUTION
assert (hasattr(xP,'__call__'))
assert (hasattr(yP,'__call__'))
assert (hasattr(eC,'__call__'))
assert (hasattr(sigmaG,'__call__'))
# trajectoire et moment cinétique et energie cinetique
T = np.linspace(0,6*np.pi,100)
XP = xP(T)
YP = yP(T)
EC = eC(T)*np.ones(T.size)
SigmaG = sigmaG(T)*np.ones(T.size)
plt.figure(figsize=(10,12))
plt.subplot(2,1,1)
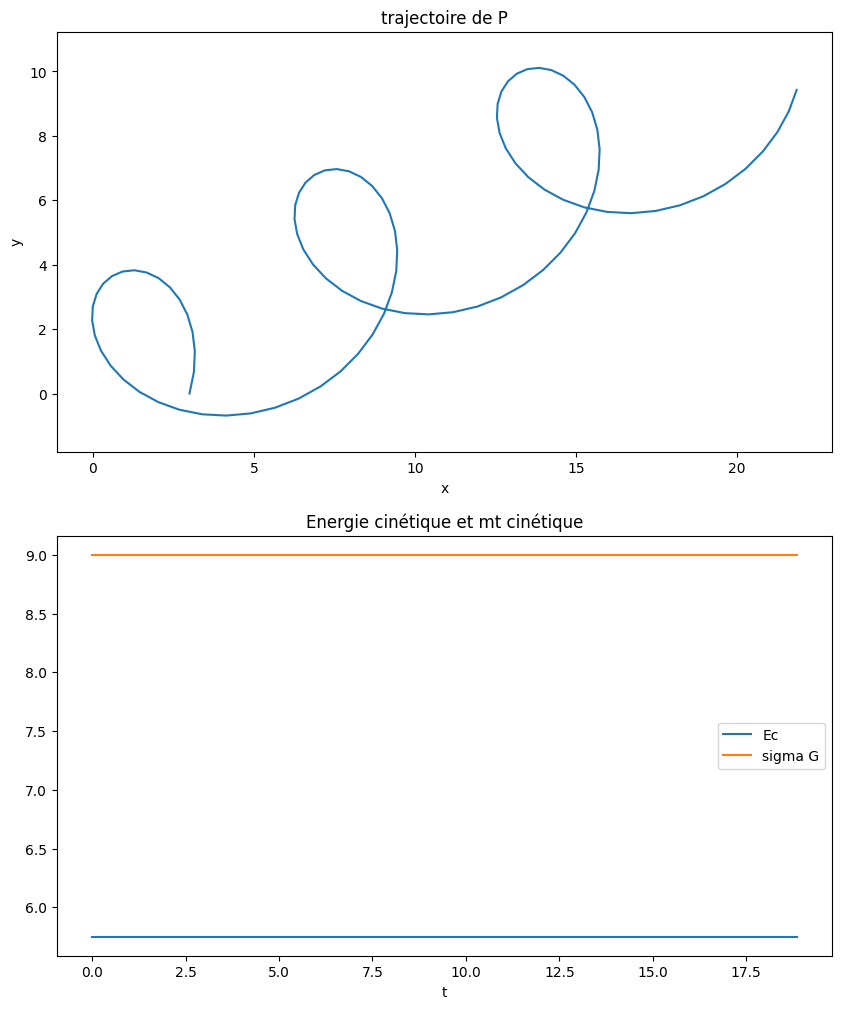
plt.title("trajectoire de P")
plt.plot(XP,YP)
plt.xlabel('x')
plt.ylabel('y')
plt.axis('equal')
plt.subplot(2,1,2)
plt.title("Energie cinétique et mt cinétique")
plt.plot(T,EC,label="Ec")
plt.plot(T,SigmaG,label="sigma G")
plt.xlabel('t')
plt.legend();
12.9.1. Analyse du mouvement#
L’analyse du mouvement consiste dans notre cas à répondre en particulier aux questions suivantes!
Décrire la trajectoire obtenue: dans notre cas regarder ce qui se passe pour les différentes valeurs de d.
Dans quel cas le mouvement étudié correspond à celui d’une toupie roulant sans glisser le long d’un mur vertical.
Que peut-on déduire du tracer de l’énergie cinétique et du moment cinétique en G ?
La toupie est-elle soumise à des forces ou des couples ?
Si la trajectoire de la toupie est circulaire avec une vitesse de rotation constante, en est-il de même ? On pourra s’inspirer du système solaire pour répondre à la question.
12.9.2. Entrez ici votre analyse#
Ecrire mon analyse
pas de force ni de couple extérieur
dans le cas vg = omega*d alors la toupie roule dans glisser le long d’une paroi