5. Rappel sur les EDO#
Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1
%matplotlib inline
import numpy as np
import sympy as sp
from sympy.plotting import plot
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display
5.1. Introduction#
définition: une Equation Différentielle Ordinaire (EDO) est une équation avec pour inconnue une fonction \(y(t)\) d’une variable \(t\), qui fait intervenir la fonction et ses dérivées par rapport à t.
Les équations différentielles ordinaires sont des outils indispensables pour l’étude du mouvement de système. Le principe fondamental de la dynamique conduit naturellement à l’écriture d’EDO pour décrire le mouvement du système.
Même si on ne sait pas résoudre analytiquement toutes les EDO, il est important de connaître les propriétés de ces EDO et des solutions.
5.1.1. Ordre d’une EDO#
Les EDO sont classées suivant leur ordre n, i.e. le degré maximal de dérivation intervenant dans l’EDO:
EDO d’ordre 1 :
l’EDO fait intervenir \(y(t)\) et \(\dot{y}(t)\) uniquement. La forme canonique explicite s’écrit :\[ \dot{y} = f(y(t),t) \]EDO d’ordre 2 :
l’EDO fait intervenir \(y(t)\) , \(\dot{y}(t)\) et \(\ddot{y}(t)\). La forme canonique explicite s’écrit :\[ \ddot{y} = f(y(t),\dot{y}{t},t) \]
5.1.2. Propriétés#
EDO linéaire
il existe une méthode générale pour trouver la solution
La solution est une combinaison linéaire de solutions élémentairesEDO non-linéaire
il n’existe pas de méthode générale pour trouver la solution
questions: déterminer quelles sont les EDO linéaires
5.1.3. Généralisation : système d’EDO#
Au lieu d’une fonction scalaire \(y(t)\), on considère une fonction vectorielle \(Y(t)\), dont les composantes \(y_i(t)\) sont des fonctions scalaires. On montre que l’on peut se ramener avec un changement de variable à un système d’EDO d’ordre 1:
Un système d’EDO d’ordre 1 d’inconnue \(Y(t)\) (\(Y\) fonction vectorielle de dimension n) est un système de n équations différentielles :
qui s’écrit en notant \(y_i(t)\) les composantes de \(Y(t)\) et \(f_i\) les composantes de \(F\)
On distingue 2 cas:
les systèmes découplés , dans lesquels \(f_i\) ne dépend que \(y_i\). Les équations sont indépendantes et peuvent donc être résolues indépendamment.
les systèmes couplés , dans lesquels \(f_i\) dépend de toutes les composantes de \(Y\). Les équations sont liées et doivent être résolues ensemble.
5.2. Equation différentielle (EDO) d’ordre 1#
5.2.1. EDO d’ordre 1: forme générale explicite#
5.2.2. EDO d’ordre 1 linéaire homogène#
La solution est triviale pour \(a\in\mathbb{R}\):
Le comportement asymptotique de \(y(t)\) dépend du signe de a:
si a>0 alors \(y(t)\rightarrow \infty\)
si a<0 alors \(y(t)\rightarrow 0\)
On peut généraliser au cas \(a\in\mathbb{C}\), i.e. \(a = x + \imath y\)
5.2.3. EDO d’ordre 1 linéaire non homogène#
solution = solution générale homogène + solution particulière
solution particulière : méthode variation de la constante
solution particulière évidente
from sympy import Derivative, Eq, dsolve
t = sp.symbols('t')
y = sp.symbols('y',cls=sp.Function)
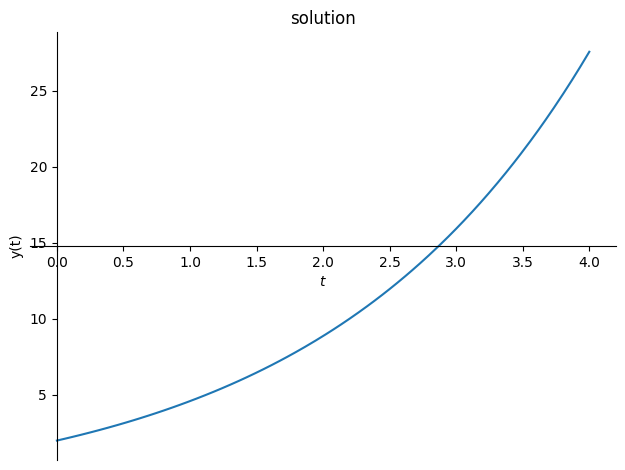
eq = Eq(Derivative(y(t),t),y(t)/2+1)
CI = {y(0):2}
display(eq,CI)
sol = dsolve(eq,ics=CI)
display(sol)
plot(sol.rhs,(t,0,4),title="solution",ylabel="y(t)");
{y(0): 2}
5.2.4. Système d’équations différentielles d’ordre 1#
5.2.4.1. système EDO d’ordre 1: forme générale#
Si le système est découplé, on se ramène au cas précédent (cas simple).
5.2.4.2. Exemple 1: système linéaire couplé#
soit
Si \(A\) était diagonale, le système serait découplé, et la résolution simple. On va donc rentre \(A\) diagonale par changement de repère, en calculant les valeurs propres \(\lambda\) et vecteurs propres \(\Lambda\) de \(A\):
Les valeurs propres \(\lambda\) sont solutions de
et sont donc les racines du polynôme caractéristique :
Ce polynôme possède 2 racines : \(\lambda_1 = \imath \omega\) et \(\lambda_2 = -\imath \omega\)
En effectuant un changement de repère, et en se plaçant dans le repère des valeurs propres, on peut obtenir un système découplé.
Dans notre cas, on va le faire plus simplement , en faisant une combinaison linéaire des équations
En posant \(z_1 = y_2 + \imath\omega y_1\) et \(z_2 = y_2 - \imath\omega y_1\), on obtiens 2 équations inédépendantes
dont la solution générale peut s’écrire sous la forme \(z_1 = 2a\omega e^{\imath \omega t} \) et \(z_2 = 2b\omega e^{-\imath \omega t} \)
qui fournit la solution générale du système initiale:
Les constantes \(a\) et \(b\) sont fournit par les conditions initiales: p.e. pour \(y_1(0)=1\) et \(y_2(0)=0\) , on trouve \(a=\imath/2\) et \(b=-\imath/2\) ce qui donne la solution: $\( y_1(t) = \cos(\omega t) \mbox{ et } y_2(t) = -\omega \sin(\omega t) \)$
from sympy import Matrix
omega = sp.symbols('omega',positive=True)
y1, y2 = sp.symbols("y_1 y_2", cls=sp.Function)
Y = Matrix([[y1(t)],[y2(t)]])
A = Matrix([[0,1],[-omega**2,0]])
EQ = Eq(Derivative(Y,t).doit(),A*Y)
# CI
Y0 = Matrix([[1],[0]])
display("systeme EDO",EQ, "CI",Y0)
VP = A.eigenvects()
display("VP 1:",VP[0][0],VP[0][2][0])
display("VP 2:",VP[1][0],VP[1][2][0])
l1 = VP[0][0]
l2 = VP[1][0]
D = Matrix([[l1,0],[0,l2]])
display("Matrice diagonale D v.p. :",D)
L1 = VP[0][2][0]
L2 = VP[1][2][0]
Q = Matrix([[L1[0],L2[0]],[L1[1],L2[1]]])
display("Matrice de passage Q et Q^-1=",Q,Q.inv())
display("A = Q D Q^-1",Q * D * Q.inv())
z1, z2 = sp.symbols("z_1 z_2", cls=sp.Function)
Z = Matrix([[z1(t)],[z2(t)]])
display("changement de variable ",Eq(Z,Q.inv()*Y))
EQ1 = Eq(Derivative(Z,t).doit(),D*Z)
Z0 = Q.inv()*Y0
display("EDO diagonalisé",EQ1,"C.I",Z0)
sol1 = dsolve(Derivative(z1(t),t)-l1*z1(t),ics={z1(0):Z0[0]})
sol2 = dsolve(Derivative(z2(t),t)-l2*z2(t),ics={z2(0):Z0[1]})
display("solution en z:",sol1,sol2)
Ys = Q*Matrix([[sol1.rhs],[sol2.rhs]])
Ys[0] = Ys[0].simplify(); Ys[1] = Ys[1].simplify()
display("solution en Y",Eq(Y,Ys))
'systeme EDO'
'CI'
'VP 1:'
'VP 2:'
'Matrice diagonale D v.p. :'
'Matrice de passage Q et Q^-1='
'A = Q D Q^-1'
'changement de variable '
'EDO diagonalisé'
'C.I'
'solution en z:'
'solution en Y'
5.2.4.3. EDO d’ordre 1 linéaire homogène#
si \(\mathbf{A}\) possède n valeurs propres réelles \(\lambda_k\), la solution générale s’écrit
les \(\alpha_k\) sont solution du système linéaire
On a donc diagonalisée la matrice \(\mathbf{A} = Q*\mathbf{D}*Q^{-1}\) pour obtenir un système EDO linéaire découplée $\( \dot{Z} = \mathbf{D} Z \mbox{ avec } Z = \mathbf{Q}^{-1} {Y} \)$
5.2.4.4. Exemple 2#
from sympy import Matrix
y1, y2 = sp.symbols("y_1 y_2", cls=sp.Function)
Y = Matrix([[y1(t)],[y2(t)]])
A = Matrix([[2,-1],[-1,2]])
EQ = Eq(Derivative(Y,t).doit(),A*Y)
Y0 = Matrix([[2],[-1]])
display("systeme EDO",EQ, "CI",Y0)
VP = A.eigenvects()
l1 = VP[0][0]
l2 = VP[1][0]
D = Matrix([[l1,0],[0,l2]])
display("Matrice diagonale D v.p. :",D)
L1 = VP[0][2][0]
L2 = VP[1][2][0]
Q = Matrix([[L1[0],L2[0]],[L1[1],L2[1]]])
display("Matrice de passage Q=",Q)
display("Q D Q^-1",Q * D * Q.inv())
z1, z2 = sp.symbols("z_1 z_2", cls=sp.Function)
Z = Matrix([[z1(t)],[z2(t)]])
display("changement de variable ",Eq(Z,Q.inv()*Y))
EQ1 = Eq(Derivative(Z,t).doit(),D*Z)
Z0 = Q.inv()*Y0
display("EDO diagonalisé",EQ1,"C.I",Z0)
sol1 = dsolve(Derivative(z1(t),t)-l1*z1(t),ics={z1(0):Z0[0]})
sol2 = dsolve(Derivative(z2(t),t)-l2*z2(t),ics={z2(0):Z0[1]})
display("solution en z:",sol1,sol2)
Ys = Q*Matrix([[sol1.rhs],[sol2.rhs]])
display("solution en Y",Eq(Y,Ys))
'systeme EDO'
'CI'
'Matrice diagonale D v.p. :'
'Matrice de passage Q='
'Q D Q^-1'
'changement de variable '
'EDO diagonalisé'
'C.I'
'solution en z:'
'solution en Y'
5.3. Equation différentielle (EDO) d’ordre 2#
5.3.1. EDO d’ordre 2: forme générale explicite#
5.3.2. EDO d’ordre 2 linéaire homogène#
Cas général:
racines du polynôme caractéristique \(a\lambda^2 + b\lambda + c\)
Equation en mécanique: système dynamique avec force de rappel (fonction de y), et un amortissement (fonction de \( \dot{y}\)
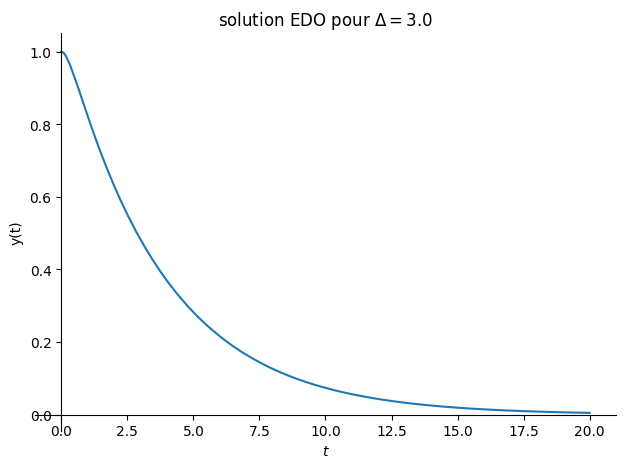
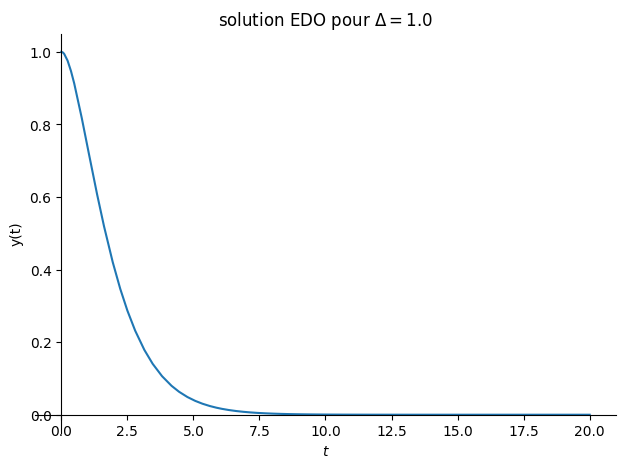
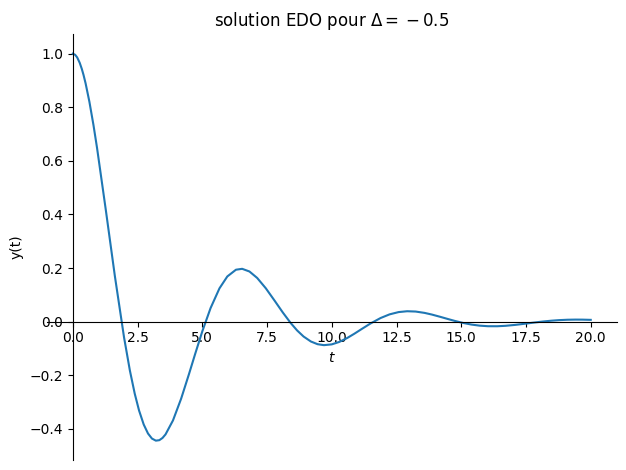
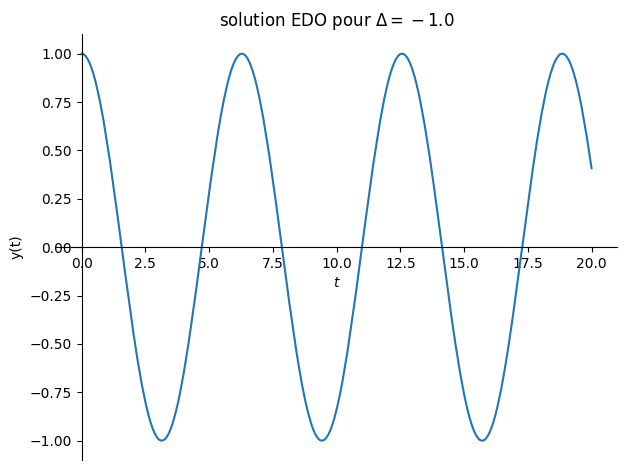
solution fonction du signe de \(\Delta = \lambda_0^2 -\omega_0^2\)
\(\Delta>0\) régime apériodique
\(\Delta=0\) régime critique
\(\Delta<0\) régime pseudo-péroidique
lambda0, omega0 = sp.symbols("lambda_0 omega_0")
eq = Derivative(y(t),t,t) + 2*lambda0*Derivative(y(t),t) + omega0**2*y(t)
display("EDO ",eq)
Valnums = [None,None,None,None]
# amortie
Valnums[0]={lambda0:2,omega0:1}
# critique
Valnums[1]={lambda0:1,omega0:1}
# pseudo per.
Valnums[2]={lambda0:1/sp.S(4),omega0:1}
# periodique
Valnums[3]={lambda0:0,omega0:1}
for Valnum in Valnums:
Delta = float((lambda0*2-omega0**2).subs(Valnum))
#display(Valnum,"Delta=",Delta)
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
#display("CI:",CI)
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution :",sol)
plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");
'EDO '
'solution :'
'solution :'
'solution :'
'solution :'
5.3.3. EDO d’ordre 2 linéaire avec forçage \(f(t)\)#
solution = solution équation homogène + solution particulière
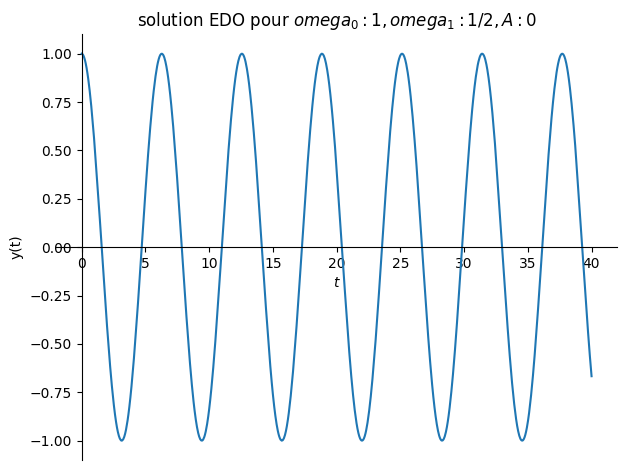
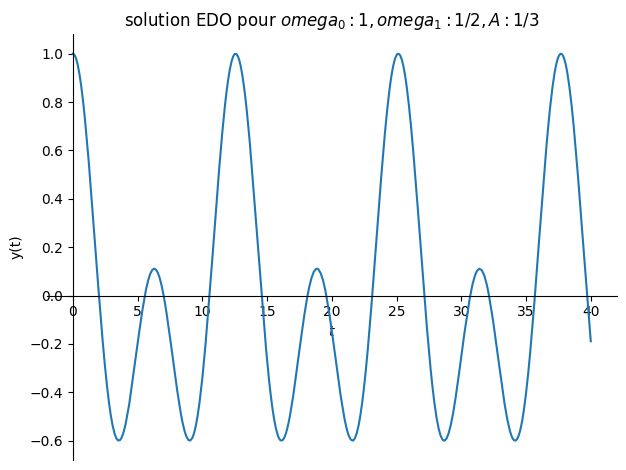
si forçage harmonique \(f(t)= A \cos(\omega_1 t)\)
la solution dépend de la valeur de \(\omega_1\) par rapport à \(\omega_0\)
si \(\omega_1 \neq \omega_0\) solution particulière \( y(t) = \alpha \cos{\omega_1 t}\)
si \(\omega_1 = \omega_0\) résonnance: solution particulière \( y(t) = t \sin{\omega_0 t}\)
omega1, A = sp.symbols("omega_1 A")
eq = Eq(Derivative(y(t),t,t) + omega0**2*y(t),A*sp.cos(omega1*t))
display("EDO ",eq)
Valnums = [None,None,None,None]
# sans forcage
Valnums[0]={omega0:1,omega1:1/sp.S(2),A:0/sp.S(3)}
# avec forcage
Valnums[1]={omega0:1,omega1:1/sp.S(2),A:1/sp.S(3)}
# avec forcage +
Valnums[2]={omega0:1,omega1:6/sp.S(5),A:1/sp.S(3)}
# resonnance
Valnums[3]={omega0:1,omega1:1,A:1/sp.S(3)}
#
for Valnum in Valnums:
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");
'EDO '
'solution: '
'solution: '
'solution: '
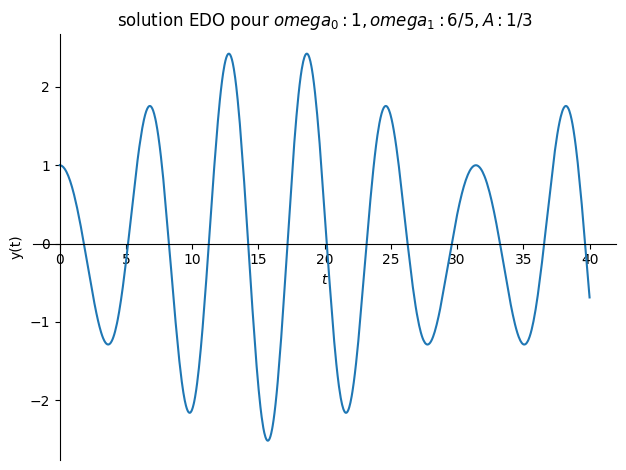
'solution: '
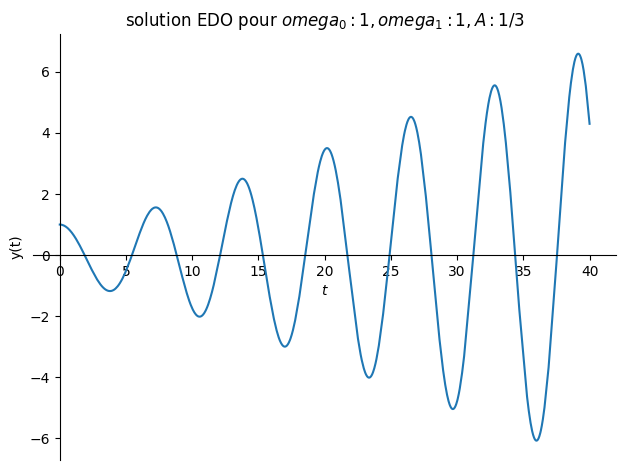
5.3.4. Transformation en EDO d’ordre 1#
Tous système d’équations différentielles peut se mettre sous la forme générique d’un système différentielle d’ordre 1
La transformation utilise un changement de variable
pour une EDO d’ordre n, on prend comme inconnues la fonction et toutes les dérivées jusqu’à l’ordre n-1
Important cette forme d’EDO d’ordre 1 est la forme générique pour la résolution numérique des EDO
5.3.4.1. transformation EDO d’ordre 2#
équation générique d’ordre 2
système d’ordre 1 équivalent
5.3.4.2. exemple#
équation d’un système dynamique sans amortissement:
transformation en EDO d’ordre 1
valeurs propres:
équation caractéristique
\[\det(\lambda Id -A) = \lambda^2 + \omega_0^2 = 0\]2 racines complexes conjuguées \(\lambda = \pm i \omega_0 \)
d’où la solution générale
\[ y(t) = Z_1 e^{i \omega_0 t} + Z_2 e^{- i \omega_0 t} \]qui correspond à la solution périodique
\[ y(t) = A \cos{\omega_0 t} + B \sin{\omega_0 t} \]
5.4. Résolution numérique des EDO#
transformation en un système d’EDO d’ordre 1
résolution d’EDO d’ordre 1 :
5.4.1. méthode d’Euler#
recherche de la solution \(y=F(t)\) de l’EDO \(\frac{dy}{dt} = f(y(t),t) \)$
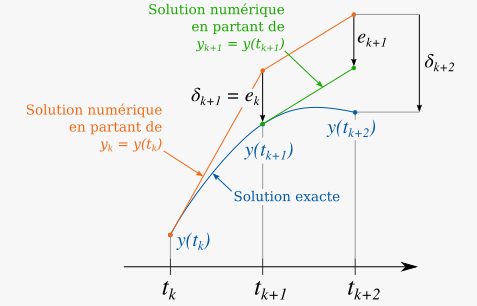
choix pas de discrétisation \(h=dt\)
calcul d’une solution approchée aux instants \(t= 0, h, 2h, .. kh\)
notation \(t_k = k h\), solution approchée \(y_k \approx F(t_k)\)
calcul itératif de \(y_{k+1}\) en fonction de \(y_k\) par discrétisation de l’EDO
5.4.2. algorithme d’Euler#
données: fonction second membre
f(y,t)parametres temps total
Td’intégration et nbre de pas d’intégrationnh= T/n calcul du pas d’intégrationY= tableau dimension n+1 solution approchée:Y[0] = y0 condition initiale t = 0 pour k de 1 a n Y[k] = Y[k-1] + h*f(Y[k_1],t) t = t + h fin boucle
5.4.3. méthode de Runge Kutta 2#
pour améliorer la précision de la solution approchée (ordre 1 avec Euler), on va utiliser une discrétisation plus précise de la dérivée entre \(t_k\) et \(t_k+h\), en calculant la valeur au milieu de l’intervalle à \(t_{k+1/2} = t_k + h/2\) à l’aide de la formule de RungeKutta 2 suivante:
dans laquelle la valeur inconnue \(y_{k+1/2}\) est calculée avec la méthode d’Euler
5.4.4. algorithme de Runge Kutta 2#
la boucle d’itération de Runge Kutta 2 s’écrit
Y[0] = y0 condition initiale
t = 0
pour k de 1 a n
ym = Y[k-1] + h/2*f(Y[k_1],t)
Y[k]= Y[k-1] + h*f(ym,t+h/2)
t = t + h
fin boucle
