Bonnes pratiques en informatique scientifique

2. Bonnes pratiques en informatique scientifique#

Marc BUFFAT , Université Claude Bernard Lyon 1

xkcd GOTO

(C) graphique issu du site xkcd

2.1. Workflow du calcul scientifique#

Le workflow du calcul scientifique le plus courant est constitué de scripts qui appellent des données, des programmes et d’autres entrées et produisent des sorties pouvant inclure des visualisations et des résultats analytiques. Ces scripts peuvent être implémentés dans des programmes tels que R ou MATLAB, et maintenant de plus en plus Python avec une interface en ligne de commande, ou plus récemment en utilisant des applications Web telles que les Notebooks Jupyter.

Le développement est généralement basé sur une construction itérative, avec une validation à chaque étape, privilégiant l’assemblage de solutions simples pour résoudre des problèmes complexes : small is beautiful

L’approche utilise la méthode REPL suivante: Read-Eval-Print Loop

  1. Définition d’une solution algorithmique

  2. Écriture du code

  3. Exécution avec analyse (print) et validation

  4. Si besoin corriger et Répéter

2.1.1. règles de programmation#

  1. définir les données et les résultats à obtenir

  2. chercher une solution algorithmique

  3. écrire du code python de haute qualité (Writing high-quality Python code)

    • commentaire (docstring)

    • privilégier la simplicité

    • compréhensible

  4. tester pour valider

  5. connaître les variables et fonctions du problème

2.1.2. Zen du python#

# zen du python
import this

The Zen of Python, by Tim Peters

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!

2.2. Bonnes pratiques#

  1. Connaitre son environement de travail

  2. Apprendre les bases du shell Unix (interpréteur de ligne de commandes)

  3. Bien connaître le langage Python 3

  4. Ecrire du code Python lissible, claire et de qualité

  5. Vérifier et valider vos proagrammes

  6. Et surtout faites preuve de rigueur

2.3. Connaitre son environnement informatique#

Pour connaître le système d’exploitation (opérating system OS ) utilisé, le système de fichiers …, on utilise des commandes du shell (bash sous Unix) en utilisant dans une cellule le mot clé %%bash

2.3.1. commandes du shell (interpréteur de commandes)#

pour avoir une dopcumentation en ligne d’une commande, p.e. whoami

     man whoami

%%bash
# nom utilisteur
whoami

buffat

%%bash
# système OS
uname -a

Linux p2chpd-visu2 5.15.0-121-generic #131-Ubuntu SMP Fri Aug 9 08:29:53 UTC 2024 x86_64 x86_64 x86_64 GNU/Linux

%%bash
# processeur
head -5 /proc/cpuinfo 

processor	: 0

vendor_id	: GenuineIntel

cpu family	: 6

model		: 94

model name	: Intel(R) Core(TM) i5-6500 CPU @ 3.20GHz

%%bash
# memoire 
head -5  /proc/meminfo

MemTotal:       32789936 kB

MemFree:        13064984 kB

MemAvailable:   27383408 kB

Buffers:          928356 kB

Cached:         12931964 kB

2.3.2. système de fichiers, répertoire#

%%bash
# liste de tout les disques du système
df

Sys. de fichiers                               blocs de 1K    Utilisé  Disponible Uti% Monté sur

tmpfs                                              3278996       2076     3276920   1% /run

/dev/sdb1                                         60159876   34890096    22181396  62% /

tmpfs                                             16394968          0    16394968   0% /dev/shm

tmpfs                                                 5120          4        5116   1% /run/lock

tmpfs                                             16394968          0    16394968   0% /run/qemu

/dev/sda1                                        240116872  200385368    27508132  88% /data

/dev/sdb2                                         81209800   70453372     6585268  92% /home

/dev/sdc1                                        960310988  126440012   785016552  14% /home/sauvegarde

/dev/sdb5                                         76712256   54782400    18023656  76% /opt

ufrmeca2bis.univ-lyon1.fr:/export/softs/x86_64 23437780992 4100772160 19337008832  18% /softs/x86_64

tmpfs                                              3278992         52     3278940   1% /run/user/0

tmpfs                                              3278992       2484     3276508   1% /run/user/1000

%%bash
# affiche le répertoire courant 
pwd

/data/cours/MGC2028L/cours

%%bash
# caractéristique d'un fichier
ls -al testPoint.py
file testPoint.py

ls: impossible d'accéder à 'testPoint.py': Aucun fichier ou dossier de ce nom

testPoint.py: cannot open `testPoint.py' (No such file or directory)

2.3.3. quelques commandes classiques#

  • copy cp

  • déplace mv

  • efface rm

  • création répertoire mkdir

  • parcourir cd

  • affiche fichier cat , head , tail

  • recherche chaine dans un fichier grep

shell script: automatisation

2.4. Recherche d’erreurs (debugging)#

Note

Everyone knows that debugging is twice as hard as writing a program in the first place. So if you’re as clever as you can be when you write it, how will you ever debug it? Don’t comment bad code—rewrite it.

Brian Kernighan (auteur du livre C programming language)

  • les erreurs sont inévitables : nous écrivons donc tous du code avec des erreurs

  • apprenez donc à vérifier et tester systématiquement votre code

  • Keep It Simple, Stupid (KISS) : gardez-le simple, stupide

  • commentez et explicitez votre code

  • vérifiez simplement avec la fonction print

  • après ces étapes de base, si vous ne trouvez pas l’erreur, on peut utiliser un débugueur, qui est un outil permettant d’exécuter le code et d’afficher la valeur des variables

2.4.1. Utilisation d’un IDE (type spyder)#

Un IDE (environnement logiciel de développement) est un outil extrêmement puissant utilisé par les développeurs pour l’écriture de codes complexes.

Pour des codes simples, il est sans doute trop puissant, et l’on préférera utiliser un outil plus simple, mème si moins sophistiqué.

2.4.2. Débugueur intégré#

les dernières versions de jupyterlab intègre un débugueur intégré offrant des possibilités intéressantes.

Pour activer le débugueur, ouvrir une notebook IPython ou un programme python dans JupyterLab, puis cliquer sur l’icône bug dans le coin supérieur droit:

débugueur

Une fois le débugueur activé, on active la fenêtre de debug à droite en cliquant sur l’icône bug dans la colonne de droite, qui fait apparaître différents panneaux

Débugueur

panneau Breakpoints

  • Mettre des points d’arrêts (breakpoint) dans le code python, ce qui permet de stopper le programme en cours d’exécution. Pour cela, déplace le curseur juste avant le numéro de ligne (un point rouge apparait). Pour mettre un point d’arrêt, il suffit alors de cliquer et le point rouge reste alors fixe

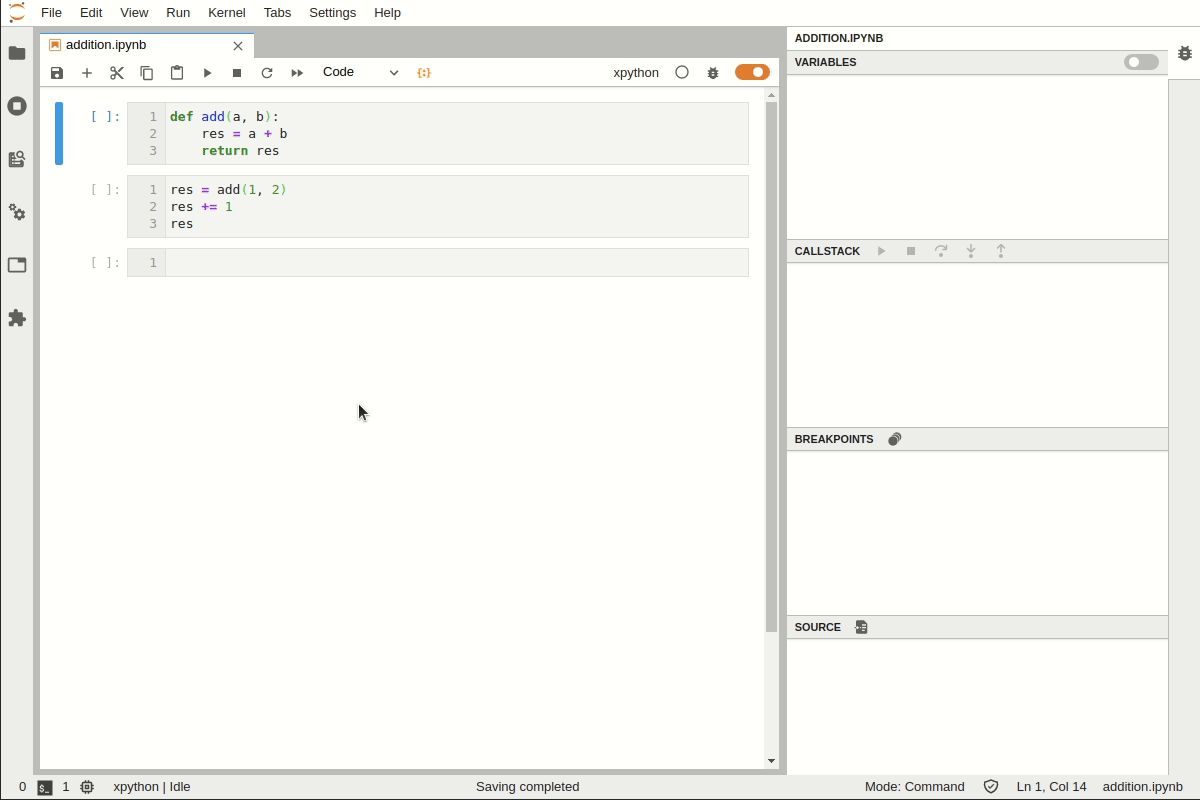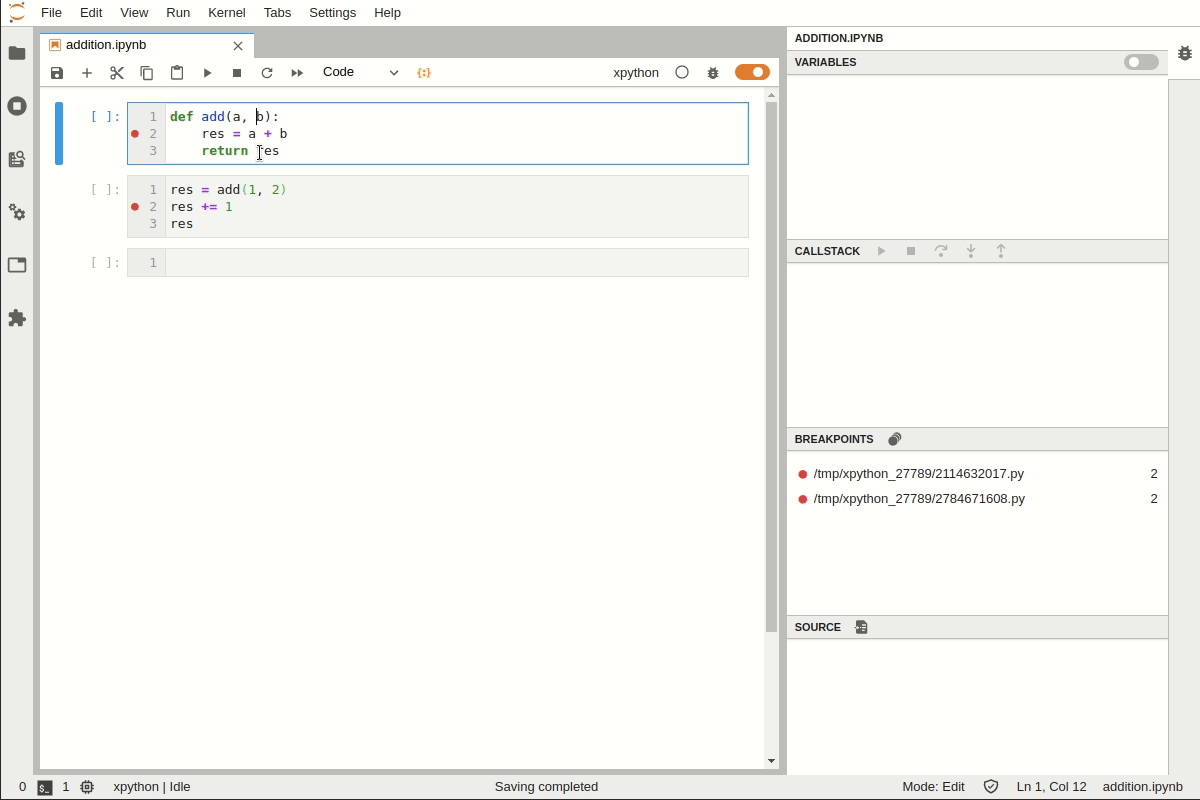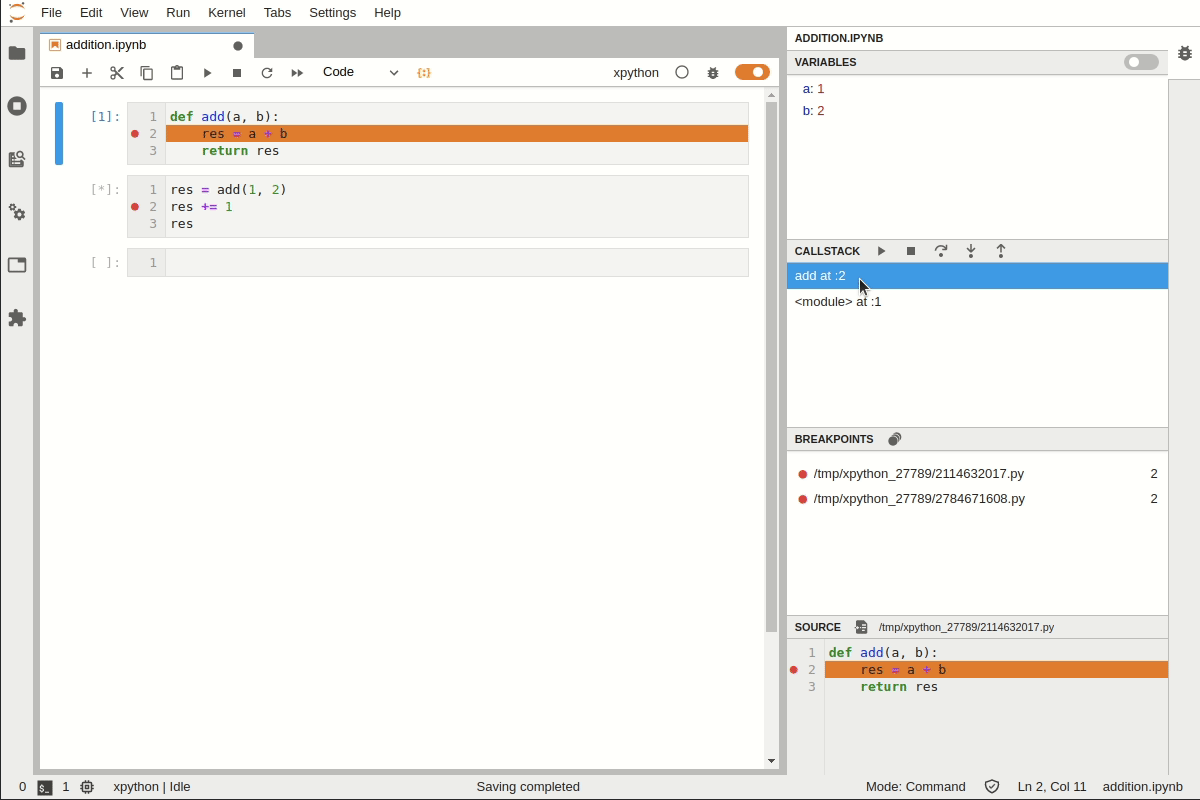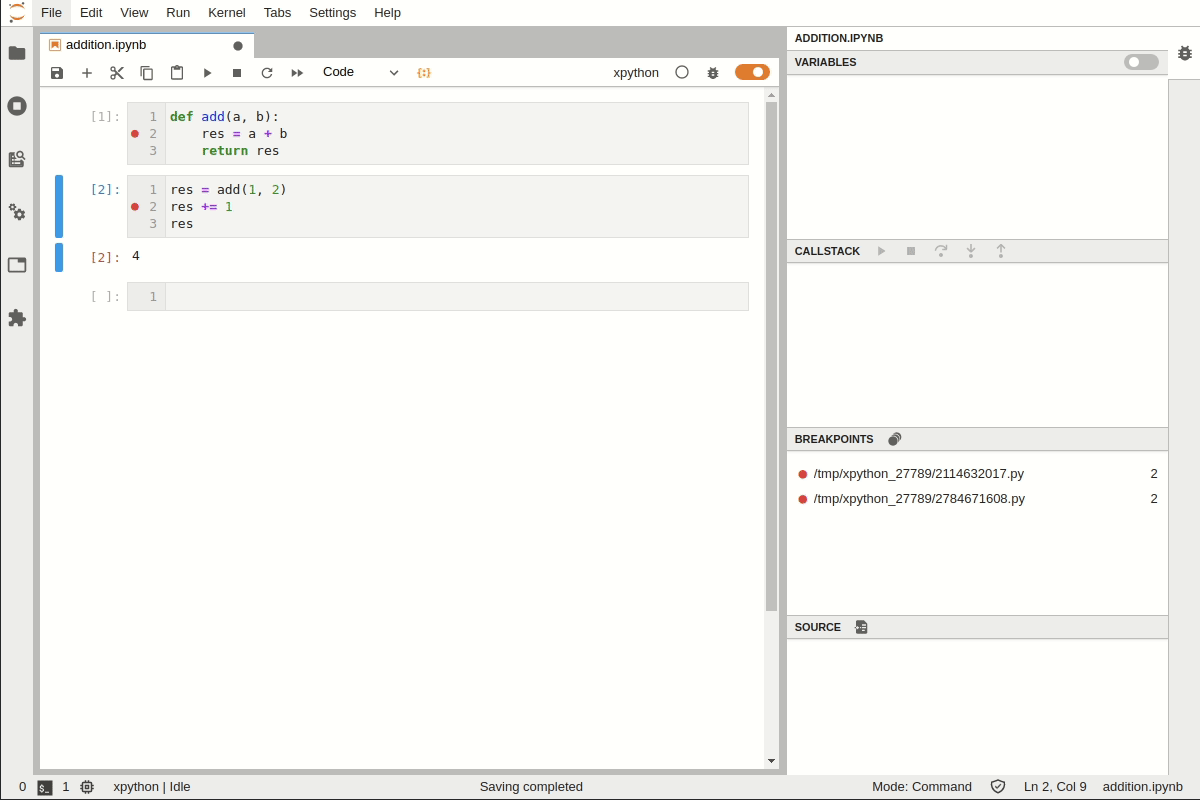
panneau Call Stack

  • Vous pouvez entrer dans le code et poursuivre l’exécution à l’aide des actions de débogage : exécuter le programme pas à pas

panneau Variables

  • Permet d’afficher la liste et les valeurs des variables du code. Les variables peuvent être explorées à l’aide d’une vue arborescente et d’une vue tableau :

panneau Source

  • Le panneau source affiche la source du fichier en cours de débogage

Important

Voici un screencast pour activer le débogueur et configurer des points d’arrêt extrait de la documentation jupyterlab

screencast

2.5. Exemple: courbe de Lissajous#

Une courbe de Lissajous (d’après le physicien français « Jules Antoine Lissajous ») est une courbe paramétrique du plan dont les composantes sont des fonctions périodiques du paramètre (en générale le temps en physique, et que l’on peut observer avec un oscilloscope).

Le programme Python suivant lissajous.py trace les courbes de Lissajous suivantes

(2.1)#\[\begin{eqnarray} x(t) &=& \sin{(\frac{2\pi}{p} t)}\\ y(t) &=& \sin{(\frac{2\pi}{q} t + \phi)} \end{eqnarray}\]

Le rapport \(n=\frac{p}{q}\) est le paramètre de la courbe et \(\phi\) le déphassage. Le temps \(T\) de parcours de la courbe est le plus petit commun multiple de \(p\) et \(q\): $\(T=pcm(p,q)=\frac{pq}{pgcd(p,q)}\)$

2.5.1. Méthodologie#

  1. Propriétés de l’algorithme PGCD à écrire

    calcul PGCD(a,b)
    propriétés : 
       PGCD(a,a) = a    
       si a >b PGCD(a,b)=PGCD(a-b,b)
       sinon PGCD(a,b)=PGCD(a,b-a)

  1. Programme Python

  • traduction algorithme sous python

  1. Validation

  • définition des cas de validation

  • PGCD(125,125)=125

  • PGCD(9,21)=3

2.5.2. Solution algorithmique#

Algorithme PGCD(a,b)

tant que a#b
   si a>b alors a=b-a
   sinon b = b-a
retour a

# programme
def PGCD(a,b):
    """calcul du pgcd de a et b par l'algorithme d'Euclide."""
    while a!=b:
        if a>b: 
            a = a -b
        else: 
            b = b -a
    return a

# validation
assert(PGCD(123,123)==123)
assert(PGCD(9,21)==3)
assert(PGCD(28,16)==4)

# variante (optimise)
def pgcd(a, b):
    """calcul du pgcd de a et b par l'algorithme d'Euclide."""
    print(a,b)
    while b:
        a, b = b, a % b
        print(a,b)
    return a

pgcd(30,21)

30 21
21 9
9 3
3 0

3

assert(pgcd(123,123)==123)
assert(pgcd(9,21)==3)
assert(pgcd(28,16)==4)

123 123
123 0
9 21
21 9
9 3
3 0
28 16
16 12
12 4
4 0

2.5.3. Courbe de lissajous#

(2.2)#\[\begin{eqnarray} x(t) &=& \sin{(\frac{2\pi}{p} t)}\\ y(t) &=& \sin{(\frac{2\pi}{q} t + \phi)} \end{eqnarray}\]
Algorithme Lissajous(p,q,phi,N)
  periode commune T = ppcm(p,q)
  T = pq/pgcd(p,q)
  t = [0,T/(N-1),...,T]
  x = sin(2*pi/p*t)
  y = sin(2*pi/q*t + phi)
  retour t,x,y

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
def Lissajous(p,q,phi,N):
    """ calcul de N points d'une courbe de Lissajous"""
    omega1 = 2*np.pi/p
    omega2 = 2*np.pi/q
    # temps d'étude
    T = p*q/pgcd(p,q)
    t = np.linspace(0., T, N)
    # equations parametriques
    x = np.sin(omega1*t)
    y = np.sin(omega2*t+phi)
    return t,x,y

# validation
t,x,y = Lissajous(2,2,0.,100)
assert(np.all(np.abs(x-y)<1.e-8))

2 2
2 0

# application
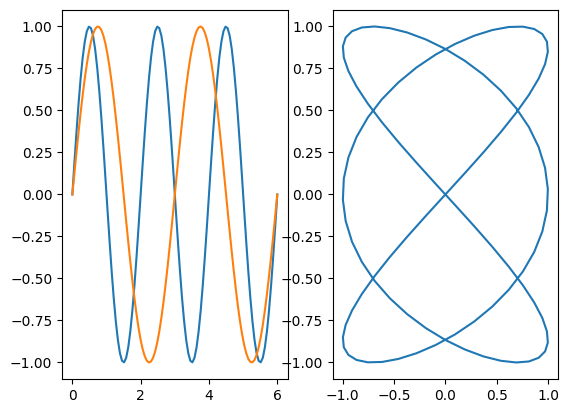
t,x,y = Lissajous(2,3,0.,100)
plt.subplot(1,2,1)
plt.plot(t,x)
plt.plot(t,y)
plt.subplot(1,2,2)
plt.plot(x,y)

2 3
3 2
2 1
1 0

[<matplotlib.lines.Line2D at 0x7fcf732f4100>]
../../_images/a89941816ae2f24eefe21e94b5a282080665176f7560395c4955794c6d2d508c.png

2.5.4. Mise sur fichier (pour réutilisation comme module)#

  1. crétaion du fichier Lissajous.py

  2. importation du module

mot clé import

%%bash
cat Lissajous.py

#! /usr/bin/env python3



import numpy as np

def PGCD(a,b):

    """calcul du pgcd de a et b par l'algorithme d'Euclide."""

    while a!=b:

        if a>b: 

            a = a -b

        else: 

            b = b -a

    return a



def Lissajous(p,q,phi,N):

    """ calcul de N points d'une courbe de Lissajous"""

    omega1 = 2*np.pi/p

    omega2 = 2*np.pi/q

    # temps d'étude

    T = p*q/PGCD(p,q)

    t = np.linspace(0., T, N)

    # equations parametriques

    x = np.sin(omega1*t)

    y = np.sin(omega2*t+phi)

    return t,x,y

# test de validation

if __name__ == "__main__":

    assert(PGCD(123,123)==123)

    assert(PGCD(9,21)==3)

    assert(PGCD(28,16)==4)

    t,x,y = Lissajous(2,2,0.,100)

    assert(np.all(np.abs(x-y)<1.e-8))

    print("Validation OK")

%%bash 
python3 Lissajous.py

Validation OK

import  Lissajous as li
t,x,y = li.Lissajous(2,3,0.,100)
plt.subplot(1,2,1)
plt.plot(t,x)
plt.plot(t,y)
plt.subplot(1,2,2)
plt.plot(x,y)

[<matplotlib.lines.Line2D at 0x7fcf6f03f3a0>]
../../_images/a89941816ae2f24eefe21e94b5a282080665176f7560395c4955794c6d2d508c.png

2.6. The END#

Contenu