EDO: analyse du mouvement de chute libre

6. EDO: analyse du mouvement de chute libre#

Marc BUFFAT, dpt mécanique, Université Lyon 1

inspiré par le cours « Engineering Computations » du Pr L. Barba (Washington Univ.)

../../../../_images/Falling_ball.jpg

6.1. Objectifs#

  • Résolution numérique d’Equation Différentielle Ordinaire (EDO)

  • Méthode d’Euler / méthode de Runge Kutta

  • Validation

  • Analyse

6.2. Expérience préliminaire (à faire en autonomie)#

Pour la conception de manège de type montagnes russes, les ingénieurs utilisent un accéléromètre car c’est l’accélération qui rend un tour de montagnes russes excitant, alors que la vitesse n’atteind que rarement une valeur supérieure à 100 km/h (27 m/s) [2].

Comment un ingénieur analyserait-il les données mesurées avec un accéléromètre?

../../../../_images/Rocket_Coaster.jpg

Les données mesurées sur une partie d’un manège de montagnes russes appelé « The rocket » sont stockées dans un fichier therocket.txt du dossier data. Ce fichier contient 2 colonnes de chiffres, le temps et la mesure de l’accélération dans la direction du mouvement.

Avec la commande unix/linux head fichier on affiche le début du fichier pour vérifier.

!head ./data/therocket.txt

  0.0000000e+000  2.7316440e-001

  1.0000000e-001  1.4411079e+000

  2.0000000e-001  2.6693138e+000

  3.0000000e-001  4.2383806e+000

  4.0000000e-001  5.6499504e+000

  5.0000000e-001  6.9489214e+000

  6.0000000e-001  8.4234922e+000

  7.0000000e-001  9.7402175e+000

  8.0000000e-001  1.1202077e+001

  9.0000000e-001  1.2641944e+001

6.2.1. Objectif#

L’objectif est de déterminer le module de la vitesse et la distance parcourue à partir des mesures d’accélération tangentielle.

Les étapes de programmation sont les suivantes:

  1. importation des bibliothèques

  2. lecture des données en utilisant loadtxt

  3. vérification en traçant les données

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
plt.rc('font', family='serif', size='14')

6.2.2. Lecture des données#

# lecture des données
filename = './data/therocket.txt'
t, a = np.loadtxt(filename, unpack=True)

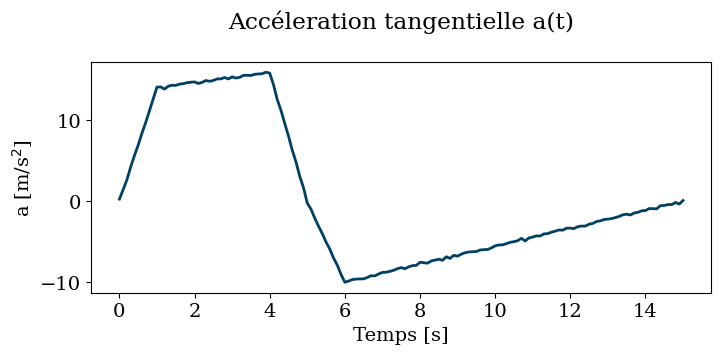
# trace de l'acceleration
plt.figure(figsize=(8, 3))
plt.plot(t, a, color='#004065', linestyle ='-', linewidth=2) 
plt.title('Accéleration tangentielle a(t)\n')
plt.xlabel('Temps [s]')
plt.ylabel('a [m/s$^2$]');
../../../../_images/d26aeb776a1eb654664cd538c8dca99f4491e728904ee7a1ac4409982cc552ae.png

6.2.3. méthode de calcul de la vitesse et de la distance parcourue#

Notre défi est maintenant de calculer la distance parcourue \(x(t)\) à partir des données d’accélération tangentielle en utilisant des dérivées numériques

A un instant \(t=t_i\), on écrit:

(6.1)#\[\begin{equation} v(t_i) = \frac{dx}{dt} \approx \frac{x(t_i+\Delta t)-x(t_i)}{\Delta t} \end{equation}\]
(6.2)#\[\begin{equation} a(t_i) = \frac{dv}{dt} \approx \frac{v(t_i+\Delta t)-v(t_i)}{\Delta t} \end{equation}\]

La clé du problème est de réaliser que si nous avons la vitesse initiale, nous pouvons utiliser les données d’accélération pour trouver la vitesse après un court intervalle de temps. Et si nous avons la position initiale, nous pouvons utiliser la vitesse connue pour trouver la nouvelle distance parcourue après un court intervalle de temps. Réorganisons l’équation d’accélération ci-dessus, en résolvant la vitesse à \(t_i + \Delta t\):

(6.3)#\[\begin{equation} v(t_i+\Delta t) \approx v(t_i) + a(t_i) \Delta t \end{equation}\]

Nous avons besoin de connaître la vitesse et l’accélération à l’instant initial, \(t_0\), puis nous pouvons calculer la vitesse \(v (t_i + \Delta t)\). Pour le parcours de manège de montagnes russes étudié, on suppose que la vitesse initiale est nulle et que la distance parcourue initiale est nulle.

On peut alors commencer le calcul

6.2.4. Itération en temps#

Nous allons utiliser une instruction for pour parcourir la séquence des valeurs d’accélération, en calculant à chaque fois la vitesse et la distance parcourue à l’instant suivant. Nous appliquons l’équation précédente pour calculer \(v(t_i + \Delta t)\)

(6.4)#\[\begin{equation} v(t_i+\Delta t) \approx v(t_i) + a(t_i) \Delta t \end{equation}\]

et une équation similaire pour la distance parcourue:

(6.5)#\[\begin{equation} x(t_i+\Delta t) \approx x(t_i) + v(t_i) \Delta t \end{equation}\]

Algorithme

Les étapes de programmation sont les suivantes:

  1. détermine le pas en temps dt

  2. calcul le nbre de pas en temps N

  3. création des tableaux de vitesse v et de position x de dimension N

  4. boucle d’iterations sur N-1 pas en temps

  5. tracer du résultat

  6. analyse

# votre code
v = None
x = None
N = 0
### BEGIN SOLUTION
# pas en temps
dt = t[1]-t[0]
# nbre de pas de temps
N = len(t)
#initialize v and x arrays to zero
v = np.zeros(N)
x = np.zeros(N)
for i in range(N-1):
    v[i+1] = v[i] + a[i]*dt
    x[i+1] = x[i] + v[i]*dt
### END SOLUTION

6.2.5. tracé du résultat#

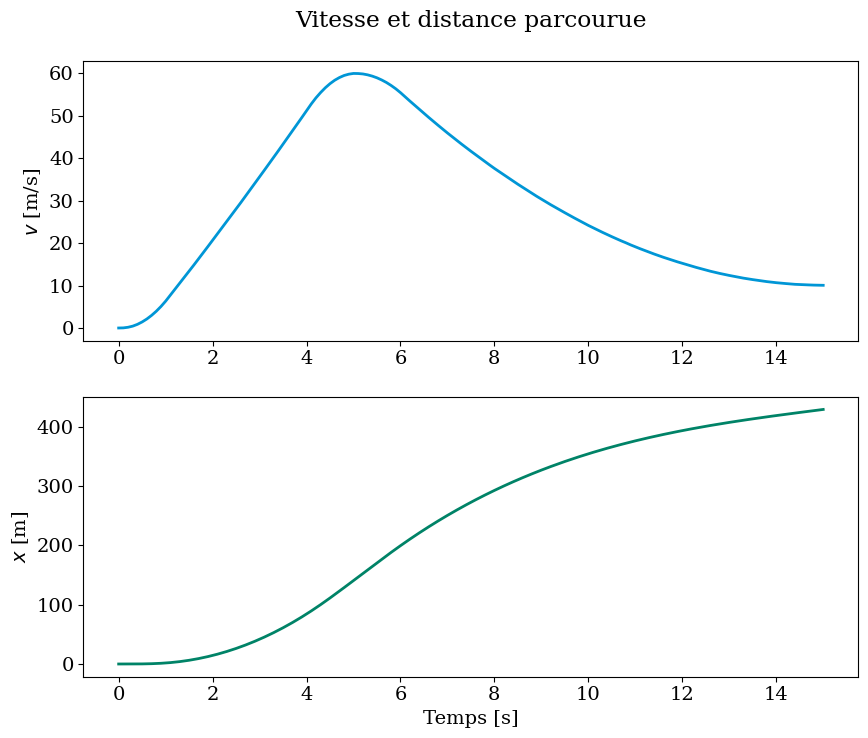
Nous avons calculé la vitesse et la position en fonction du temps à partir des données d’accélération. Nous pouvons maintenant faire les graphiques des variables calculées. Notez que nous utilisons la fonction subplot() de Matplotlib pour obtenir les deux graphiques en une seule figure. L’argument de subplot() est un ensemble de trois chiffres, correspondant au nombre de lignes, au nombre de colonnes et au numéro de la sous-figure dans une matrice de sous-figures.

# trace vitesse et la position
fig=plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.title("Vitesse et distance parcourue\n")
plt.plot(t,  v, color='#0096d6', linestyle='-', linewidth=2) 
plt.ylabel('$v$ [m/s] ')
plt.subplot(2,1,2)
plt.plot(t,  x, color='#008367', linestyle='-', linewidth=2) 
plt.xlabel('Temps [s]')
plt.ylabel('$x$ [m]');
../../../../_images/1863a232904746bc566475199d3e377a65ecfa9df998c6294cf0f64e8fbc8647.png

6.2.6. Analyse#

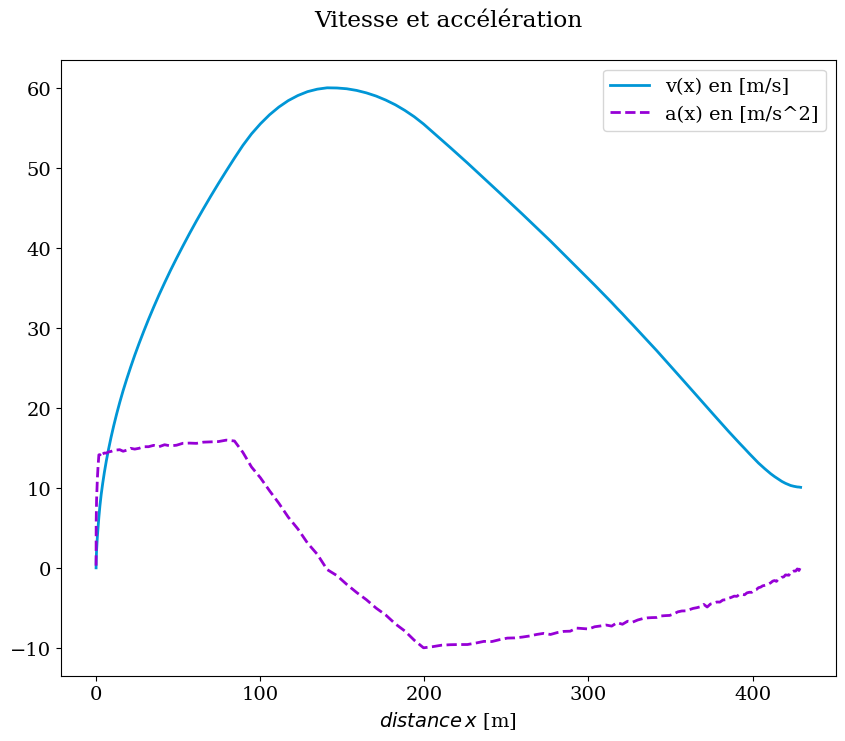
pour analyser la cinématique du manège, on trace l’accélération et la vitesse en fonction de la distance

# tracer vitesse et accélartaion fonction de la distance
fig=plt.figure(figsize=(10,8))
plt.title("Vitesse et accélération\n")
plt.plot(x,  v, color='#0096d6', linestyle='-',  linewidth=2,label="v(x) en [m/s]") 
plt.plot(x,  a, color='#9600d6', linestyle='--', linewidth=2,label="a(x) en [m/s^2]") 
plt.xlabel('$distance\,x$ [m] ')
plt.legend();
../../../../_images/53afa7989926c9b4bc574607b4b9544b0502fcef39e99674a2bec9fd6999f536.png

6.3. Méthode d’Euler pour intégrer une EDO#

La méthode que nous avons utilisée ci-dessus pour calculer la vitesse et la position à partir des données d’accélération est connue sous le nom de méthode d’Euler. L’éminent mathématicien suisse Leonhard Euler l’a présenté dans son livre « Institutionum calculi integralis » publié vers 1770 [3].

On peut comprendre comment cela fonctionne en écrivant un développement de Taylor pour \(x(t)\):

(6.6)#\[\begin{equation} x(t+\Delta t) = x(t) + \frac{d x}{dt}\Delta t + \frac{d^2 x}{dt^2}\frac{\Delta t^2}{2} + \frac{d^3 x}{dt^3}\frac{\Delta t^3}{3!}+\cdots \end{equation}\]

En remplaçant \(v = dx / dt\), on peut voir que les deux premiers termes correspondent à ce que nous avons utilisé. Cela signifie que la méthode d’Euler fait une approximation en ignorant les termes

\[\frac{d^2 x}{dt^2}\frac{\Delta t^2}{2} + \frac{d^3 x}{dt^3}\frac{\Delta t^3}{3!}+\cdots\]

Ainsi, l’erreur faite dans une étape de la méthode d’Euler est proportionnelle à \(\Delta t^2\). Puisque nous prenons \(N = T / \Delta t\) étapes (pour un instant final \(T\)), nous concluons donc que l’erreur globale est proportionnelle à \(\Delta t\).

La méthode d’Euler est une méthode du premier ordre car l’erreur d’approximation est proportionnelle à l’incrément de temps \(\Delta t\)

6.4. Chute libre: mouvement sous l’effet de la pesanteur#

Pour obtenir la vitesse et la position à partir des données d’accélération, nous devons connaître les valeurs initiales de la vitesse et de la position. Ensuite, nous pouvons appliquer la méthode d’Euler pour itérer en temps a à partir de \(t_0\), avec un incrément de temps \(\Delta t\). On obtiens ainsi une solution numérique approchée du problème aux valeurs initiales.

Considérons l’équation différentielle correspondant à un objet en chute libre.

(6.7)#\[\begin{equation} \ddot{y}=-g, \end{equation}\]

où \(g\) est l’accélération de la gravité. En introduisant la vitesse comme variable intermédiaire, nous pouvons écrire:

(6.8)#\[\begin{eqnarray} \dot{y} &=& v \nonumber\\ \dot{v} &=& -g \end{eqnarray}\]

ce qui précède est un système de deux équations différentielles ordinaires du premier ordre fonction du temps. Pour sa résolution numérique, nous avons besoin de deux conditions initiales et de la méthode d’Euler:

(6.9)#\[\begin{eqnarray} y(t_0) = y_0, \qquad y_{i+1} &=& y_i + \dot{y} \Delta t \mbox{ pour } i>0 \nonumber\\ v(t_0) = v_0, \qquad v_{i+1} &=& v_i + \dot{v} \Delta t \mbox{ pour } i>0 \end{eqnarray}\]

Ce système est tellement symétrique qu’on peut l’écrire comme une seule équation vectorielle! On combine les deux variables dépendantes en un vecteur d’inconnues, \(\mathbf{y}\):

(6.10)#\[\begin{equation} \mathbf{y} = \begin{bmatrix} y \\ v \end{bmatrix}, \end{equation}\]

et on écrit l’équation différentielle sous forme vectorielle, comme suit:

(6.11)#\[\begin{equation} \dot{\mathbf{y}} = \mathbf{F}(\mathbf{y}) \mbox{ avec } \mathbf{F}(\mathbf{y}) = \begin{bmatrix} v \\ -g \end{bmatrix}. \end{equation}\]

L’équation ci-dessus représente l’évolution au cours du temps de l’état du système \(\mathbf{y}\), à tout instant t.

Un code pour calculer la solution numérique, qui se généralise à d’autres systèmes dynamiques, consiste à écrire une fonction qui calcule le membre de droite \(\mathbf{F}(\mathbf{y})\) de l’équation différentielle (les dérivées des variables d’état), et une autre fonction qui prend un état et applique la méthode numérique pour chaque incrément de temps. La solution est ensuite calculée dans une instruction for

Algorithme

Les étapes de programmation sont les suivantes:

  1. définition de la fonction second membre, fonction du vecteur d’etat Y

     fonction chutelibre( Y )

  2. définition de la méthode d’Euler pour calculer l’évolution de l’etat Y sur un pas en temps avec la fonction second membre F comme argument

     fonction iterationEuler(Y,  F, dt)
 
     Y_suiv = Y + F(Y)*dt
     
     retour Y_suiv

  3. itération en temps pour calculer la solution numerique en fonction de la condition initiale

      sol_num[0] = Y0
  
  pour i de 0 a N-1 
  
      sol_num[i+1] = iterationEuler(sol_num[i], chutelibre, dt)

  4. analyse de la solution pour validation

def chutelibre(Y):
    '''Calcul du second membre de l'EDO de la chute libre d'un corps
    
    Arguments
    ----------    
    Y: etat du système [y v]
    
    Returns
    -------
    derivs: dérivée de l'etat dY/dt = [v -g]
    '''
    ### BEGIN SOLUTION
    dY = np.array([Y[1], -9.81])
    return dY
    ### END SOLUTION

# verification : calcul pour y = 0.1, v = 0.
### BEGIN SOLUTION
Y0 = np.array([0.1,0])
chutelibre(Y0)
### END SOLUTION

array([ 0.  , -9.81])

def iterationEuler(Y, F, dt):
    '''Iteration d'Euler pour calculer l'évolution de l'etat sur un pas en temps. 
    
    Arguments
    ---------
    Y  : vecteur d'etat a l'instant t
    F  : fonction qui calcule le second membre de l'EDO fonction de l'etat
    dt : pas en temps 
    
    Returns
    -------
    Y_suiv: valeur du vecteur d'etat après une iteration en temps a t+dt      
    '''
    ### BEGIN SOLUTION
    Y_suiv = Y + F(Y) * dt
    return Y_suiv
    ### END SOLUTION

# verification avec un dt = 0.01
### BEGIN SOLUTION
Y0 = np.array([0.1,0])
iterationEuler(Y0,chutelibre, 0.01)
### END SOLUTION

array([ 0.1   , -0.0981])

6.5. Solution numérique versus experience#

Nous disposons de mesures expéimentales sur la chute d’une balle de tennis dans le fichier fallingtennisball02.txt du répertoire data

Etapes:

  1. lecture des données des mesures t,y avec loadtxt

  2. calcul de la solution numérique au même temps t

!head ./data/fallingtennisball02.txt

   0.0000000000000000e+00   1.6000000000000001e+00
   1.0000000000000020e-03   1.5999950510001959e+00
   2.0000000000000044e-03   1.5999803020031378e+00
   3.0000000000000070e-03   1.5999557530158828e+00
   4.0000000000000053e-03   1.5999214040501974e+00
   4.9999999999999645e-03   1.5998772551225511e+00
   5.9999999999999238e-03   1.5998233062541209e+00
   6.9999999999998831e-03   1.5997595574707895e+00
   7.9999999999998423e-03   1.5996860088031455e+00
   8.9999999999998016e-03   1.5996026602864835e+00

filename = './data/fallingtennisball02.txt'
t, y = np.loadtxt(filename, unpack=True)

6.5.1. calcul de la solution numerique#

Nous devrons utiliser le même incrément de temps, que nous calculons à partir de deux échantillons du temps. La position initiale est la première valeur du tableau y, tandis que la vitesse initiale est nulle. Et nous ne prenons que la section des données avant que la balle ne rebondisse du sol, ce qui nous donne le nombre de pas en temps (ici N=576).

#time increment
dt = t[1]-t[0]
y0 = y[0] #initial position
v0 = 0    #initial velocity
N = 575   #number of steps

Maintenant, créons un nouveau tableau, appelé sol_num, qui contient les résultats de la solution numérique. Le tableau a des dimensions Nx2, chaque ligne à deux éléments contenant les variables d’état, \((y,v)\) , à un instant donné. Après avoir enregistré les conditions initiales dans le tableau de solution, nous pouvons commencer à avancer en temps avec une instruction for.

Etapes

  1. création du tableau sol_num de dimension N

  2. definition de la condition initiale

  3. iteration sur N-1 pas en temps

#initialize array
sol_num = None
### BEGIN SOLUTION
sol_num = np.zeros([N,2])
#Set intial conditions
sol_num[0,0] = y0
sol_num[0,1] = v0

for i in range(N-1):
    dt = t[i+1] - t[i]
    sol_num[i+1] = iterationEuler(sol_num[i], chutelibre, dt)

### END SOLUTION

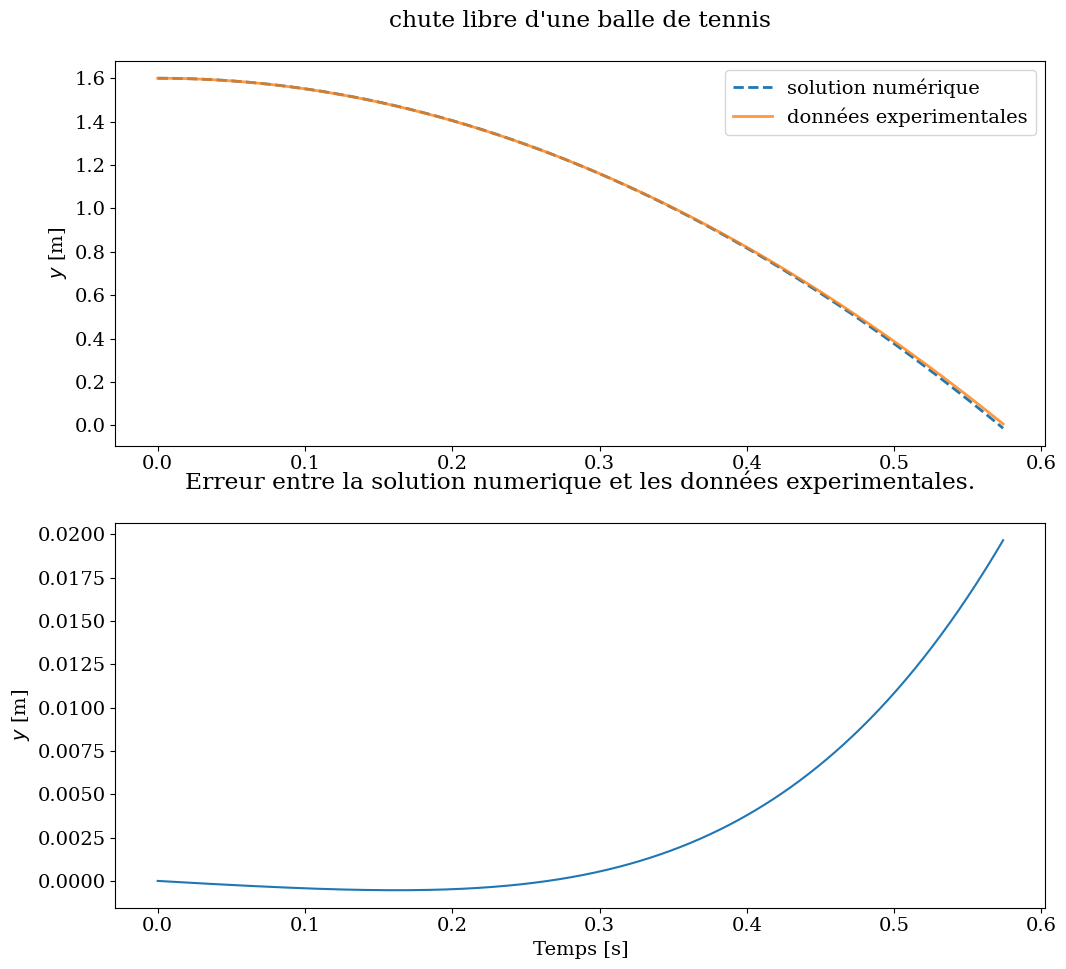
6.5.2. Validation: comparaison avec l’expérience#

Traçons sur la même figure la solution numérique et les données expérimentales.

plt.figure(figsize=(12,11))
plt.subplot(2,1,1)
plt.plot(t[:N], sol_num[:,0], linewidth=2, linestyle='--', label='solution numérique')
plt.plot(t[:N], y[:N], linewidth=2, alpha=0.8, label='données experimentales')
#plt.xlabel('Temps [s]')
plt.ylabel('$y$ [m]')
plt.title("chute libre d'une balle de tennis\n")
plt.legend();
plt.subplot(2,1,2)
plt.plot(t[:N], y[:N]-sol_num[:,0])
plt.title('Erreur entre la solution numerique et les données experimentales.\n')
plt.xlabel('Temps [s]')
plt.ylabel('$y$ [m]');
../../../../_images/52021cd10f39b0d04ce22172f2965849e0aa2f981b6ce93dbb4624bfe0383332.png

6.6. Amélioration de la méthode numérique#

La méthode numérique utilisée est uniquement d’ordre 1.

On peut utiliser une méthode plus précise à l’ordre 2, la méthode de Runge Kutta 2 qui utilise la solution numérique au milieu d’un intervalle de temps, plutôt que la solution au début.

6.6.1. Méthode de Runge Kutta 2#

L’idée de cette méthode est d’avancer la solution numérique au milieu d’un intervalle de temps avec la méthode d’Euler, en y calculant les dérivées, puis en revenant en arrière et en mettant à jour l’état du système en utilisant les dérivées du point médian. C’est ce qu’on appelle une méthode de Runge Kutta 2.

Si nous écrivons la forme vectorielle de l’équation différentielle comme:

(6.12)#\[\begin{equation} \dot{\mathbf{x}} = \mathbf{F}(\mathbf{x}), \end{equation}\]

alors la méthode numérique de Runge Kutta 2 s’écrit:

(6.13)#\[\begin{align} \mathbf{x}_{n+1/2} & = \mathbf{x}_n + \frac{\Delta t}{2} \mathbf{F}(\mathbf{x}_n) \\ \mathbf{x}_{n+1} & = \mathbf{x}_n + \Delta t \,\, \mathbf{F}(\mathbf{x}_{n+1/2}). \end{align}\]

Nous pouvons maintenant écrire une fonction Python pour mettre à jour l’état en utilisant cette méthode. Nous l’appelerons iterationRK2().

Ecrire le code Python de cette méthode dans la cellule suivante en s’inspirant du code iterationEuler()

def iterationRK2(Y, F, dt):
    '''Iteration de RungeKutta 2 pour calculer l'évolution de l'etat sur un pas en temps. 
    
    Arguments
    ---------
    Y  : vecteur d'etat a l'instant t
    F  : fonction qui calcule le second membre de l'EDO fonction de l'etat
    dt : pas en temps 
    
    Returns
    -------
    Y_suiv: valeur du vecteur d'etat après une iteration en temps a t+dt      
    '''
    ### BEGIN SOLUTION
    Y_milieu = Y + F(Y) * dt*0.5
    Y_suiv   = Y + F(Y_milieu) *dt
    return Y_suiv
    ### END SOLUTION

# verification avec un dt = 0.01
### BEGIN SOLUTION
Y0 = np.array([0.1,0])
iterationRK2(Y0,chutelibre, 0.01)
### END SOLUTION

array([ 0.0995095, -0.0981   ])

# initialize array
sol_rk2 = None
### BEGIN SOLUTION
sol_rk2 = np.zeros([N,2])
# Set intial conditions
sol_rk2[0,0] = y0
sol_rk2[0,1] = v0
for i in range(N-1):
    dt = t[i+1] - t[i]
    sol_rk2[i+1] = iterationRK2(sol_rk2[i], chutelibre, dt)
### END SOLUTION

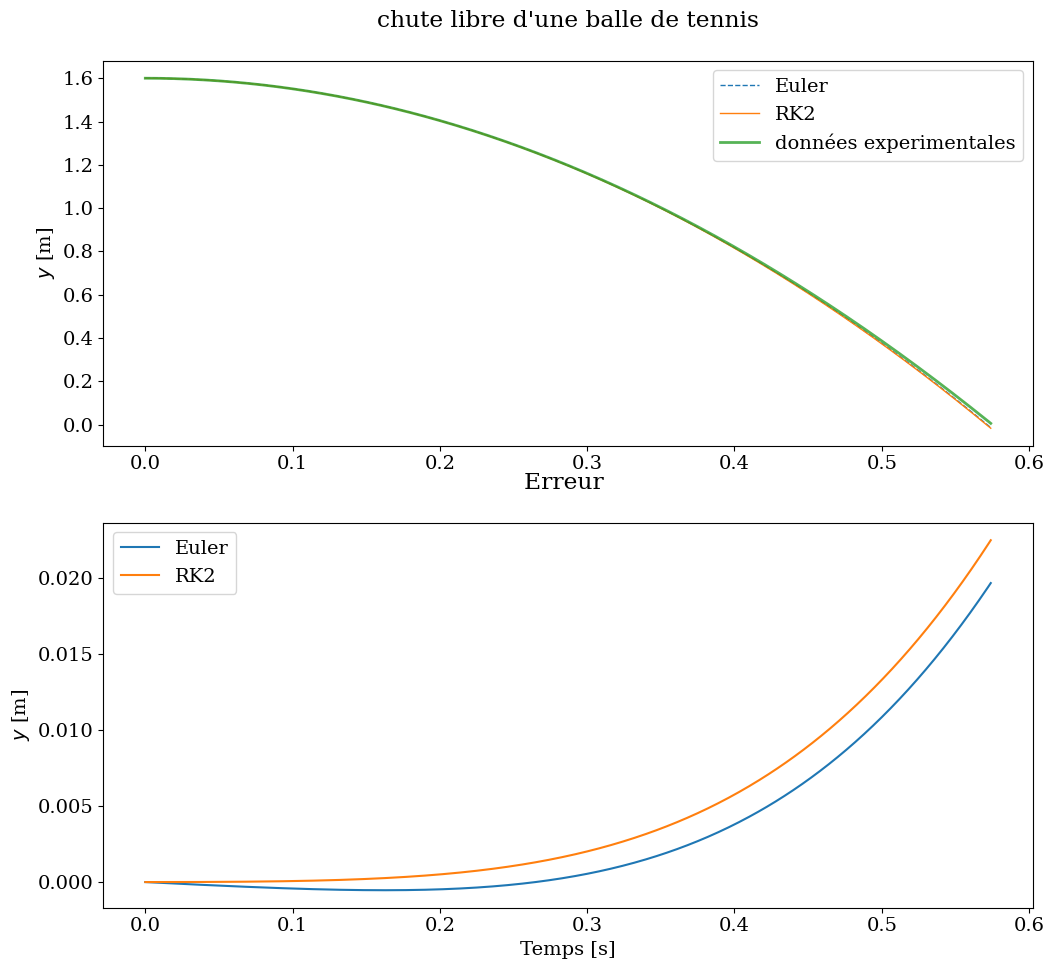
6.6.2. calcul de la solution numérique et comparaison avec Euler#

plt.figure(figsize=(12,11))
plt.subplot(2,1,1)
plt.plot(t[:N], sol_num[:,0], linewidth=1, linestyle='--', label='Euler')
plt.plot(t[:N], sol_rk2[:,0], linewidth=1, linestyle='-', label='RK2')
plt.plot(t[:N], y[:N], linewidth=2, alpha=0.8, label='données experimentales')
#plt.xlabel('Temps [s]')
plt.ylabel('$y$ [m]')
plt.title("chute libre d'une balle de tennis\n")
plt.legend();
plt.subplot(2,1,2)
plt.plot(t[:N], y[:N]-sol_num[:,0],label="Euler")
plt.plot(t[:N], y[:N]-sol_rk2[:,0],label="RK2")
plt.title('Erreur \n')
plt.xlabel('Temps [s]')
plt.ylabel('$y$ [m]')
plt.legend();
../../../../_images/f60c6d023849325a7ea22cd358ea815e0a82bbbded5b84db5311e5736c9eda52.png 
# regarder le signe
print("position finale: exp={:.4f} euler={:.4f} rk2={:.4f} theorique:{:.4f}".
      format(y[N-1],sol_num[-1,0],sol_rk2[-1,0],y0-0.5*9.81*t[N-1]**2))

position finale: exp=0.0064 euler=-0.0133 rk2=-0.0161 theorique:-0.0161

6.7. Amélioration du modèle#

L’erreur entre l’expérience et la simulation numérique n’est pas liée à une erreur numérique, mais à une erreur de modélisation.

Lorsqu’un objet se déplace dans un fluide, comme l’air, il applique une force sur le fluide, et par conséquent le fluide applique une force égale et opposée sur l’objet (troisième loi de Newton).

Cette force est une force de traînée exercée par le fluide dans la direction opposée à la vitesse. La force de traînée dépend de la géométrie de l’objet et de sa vitesse: pour une sphère, son amplitude est donnée par:

(6.14)#\[\begin{equation} F_d = \frac{1}{2} \pi R^2 \rho C_d v^2, \end{equation}\]

où \( R \) est le rayon de la sphère, \(\rho \) la densité du fluide, \(C_d \) le coefficient de traînée d’une sphère et \(v\) la vitesse.

Puisque nous avons une autre force impliquée, nous devrons repenser la formulation du problème. Les variables d’état sont toujours les mêmes (position et vitesse):

(6.15)#\[\begin{equation} \mathbf{y} = \begin{bmatrix} y \\ v \end{bmatrix}. \end{equation}\]

Mais nous ajusterons l’équation différentielle pour ajouter l’effet de la résistance de l’air. Sous forme vectorielle, on peut l’écrire comme suit:

(6.16)#\[\begin{equation} \dot{\mathbf{y}} = \mathbf{F}(\mathbf{y}) \mbox{ avec } \mathbf{F}(\mathbf{y}) = \begin{bmatrix} v \\ -g + a_{\text{drag}} \end{bmatrix}, \end{equation}\]

qui inclut désormais le terme de traînée \(a_{\text{drag}}\) qui est la force de traînée \(F_{\text{drag}}\) divisée par la masse \(m\)

(6.17)#\[\begin{equation} a_{\text{drag}} = \frac{1}{2m} \pi R^2 \rho C_d v^2 \end{equation}\]

Écrivons une nouvelle fonction chute_trainee pour calculer ce second membre modifié pour une balle de tennis qui tombe avec la prise en compte de la résistance de l’air.

Note:

Selon la Fédération internationale de tennis, ITF, le diamètre d’une balle de tennis doit être compris entre \(6,54\) et \(6,86\,\rm{cm}\), et sa masse comprise entre \(56,0\) et \(59,4\,\rm{g}\). Nous avons choisi une valeur moyenne pour chaque quantité.

def chute_trainee(Y):
    '''
    Calcul du second membre de l'EDO de la chute d'un corps 
    avec prise en compte de la trainée
    
    Arguments
    ----------    
    Y: etat du système [y v]
    
    Returns
    -------
    dY: dérivée de l'etat [v -g]
    ''' 
    R = 0.0661/2 # radius in meters
    m = 0.0577   # mass in kilograms
    rho = 1.22   # air density kg/m^3
    C_d = 0.47   # drag coefficient for a sphere
    ### BEGIN SOLUTION
    a_drag = 1/(2*m) * np.pi * R**2 * rho * C_d * (Y[1])**2
    
    dY = np.array([Y[1], -9.8 + a_drag])
    return dY
    ### END SOLUTION

6.7.1. simulation numérique#

Avec les mêmes conditions initiales que prècédemment

  1. création du tableau sol_drag de dimension N

  2. définition de la condition initiale

  3. itération sur N-1 pas en temps

# parametres
y0 = y[0] # initial position
v0 = 0    # initial velocity
N = 575   # number of steps

# initialize array
sol_drag = None
### BEGIN SOLUTION
sol_drag = np.zeros([N,2])
# Set intial conditions
sol_drag[0,0] = y0
sol_drag[0,1] = v0
for i in range(N-1):
    dt = t[i+1]-t[i]
    sol_drag[i+1] = iterationEuler(sol_drag[i], chute_trainee, dt)
### END SOLUTION

6.7.2. Tracé des résultats#

Tracés des résultats et comparaison ave la solution sans prise en compte de la traînée

plt.figure(figsize=(12,11))
plt.subplot(2,1,1)
plt.plot(t[:N], sol_num[:,0], linewidth=2, linestyle='--', label='solution sans traînée')
plt.plot(t[:N], y[:N], linewidth=2, alpha=0.6, label='données experimentales')
plt.plot(t[:N], sol_drag[:,0], linewidth=2, linestyle='--', label='solution avec traînée')
plt.title("Chute d'une balle de tennis.\n")
#plt.xlabel('Temps [s]')
plt.ylabel('$y$ [m]')
plt.legend();
plt.subplot(2,1,2)
plt.plot(t[:N], y[:N]-sol_num[:,0], label='Sans trainée')
plt.plot(t[:N], y[:N]-sol_drag[:,0],label='Avec trainée')
plt.title('Différence entre la solution numérique et les données expérimentales.\n')
plt.xlabel('Temps [s]')
plt.ylabel('$y$ [m]')
plt.legend();
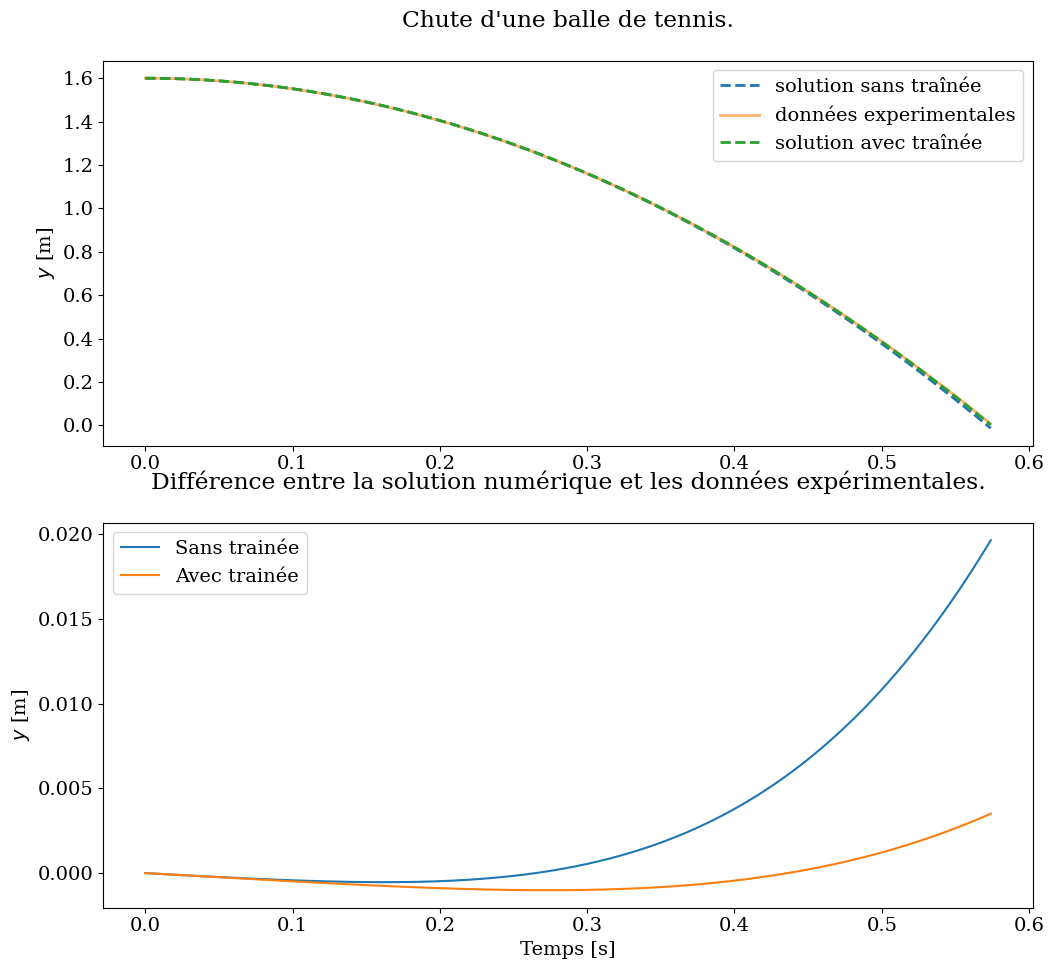
../../../../_images/478b74b2cd467e7ed1e199549ef24288e6201623e62cf26aa2c55ba582221232.png 
print("position finale: exp={:.4f} sans trainée={:.4f} avec trainée={:.4f}".
      format(y[N-1],sol_rk2[-1,0],sol_drag[-1,0]))

position finale: exp=0.0064 sans trainée=-0.0161 avec trainée=0.0029

6.8. Bilan#

Ecrire ici vos conclusions et commentaires

  • Intégration numérique d’une équation du mouvement.

  • Résolution numérique des problèmes à valeur initiale en utilisant la méthode d’Euler.

  • La méthode d’Euler est une méthode du premier ordre.

  • La prise en compte de la résistance à l’air donne un modèle plus réaliste.

6.9. References#

  1. Elementary Mechanics Using Python (2015), Anders Malthe-Sorenssen, Undergraduate Lecture Notes in Physics, Springer. Data at http://folk.uio.no/malthe/mechbook/

  2. The Physics Hyptertextbook (n/a), Glenn Elert, Acceleration

  3. Euler method. (2017, October 13). In Wikipedia, The Free Encyclopedia. Retrieved 01:21, November 10, 2017, from https://en.wikipedia.org/w/index.php?title=Euler_method&oldid=805120184

  4. Computational Physics with Python, lecture notes by Eric Ayars, California State University, Chico. Available online on the author’s website: https://physics.csuchico.edu/ayars/312/handouts/comp-phys-python.pdf

Contenu