Rappel sur les EDO du 2nd ordre

8. Rappel sur les EDO du 2nd ordre#

Marc BUFFAT, dpt mécanique, Université Claude Bernard Lyon 1

%matplotlib inline
import numpy as np
import sympy as sp
from sympy.plotting import plot, plot_parametric
import matplotlib.pyplot as plt
from IPython.core.display import HTML
from IPython.display import display

8.1. Méthode numérique de résolution d’une EDO du 2nd ordre#

Forme générale

Trouvez \(x(t)\) solution EDO ordre 2 (sous forme canonique)

\[ \ddot{x} = f(x, \dot{x},t) \]

associé à 2 conditions initiales:

\[x(t=0)=x_0, \dot{x}(t=0)=u_0\]

8.1.1. 1ere étape: transformation en un système EDO d’ordre 1#

changement de variable

\[\begin{split} Y(t) = \begin{pmatrix} x(t) \\ \dot{x}(t) \end{pmatrix} \end{split}\]

ré-écriture des équations $\( \begin{eqnarray} \dot{Y}_1 &=& Y_2 \\ \dot{Y}_2 &=& f(Y_1,Y_2,t) \\ \end{eqnarray}\)\( soit \)\( \dot{Y} = \mathbf{F}(Y(t),t) \mbox{ avec } \mathbf{F}(Y(t),t) = \begin{pmatrix} Y_2 \\ f(Y_1,Y_2,t) \end{pmatrix}\)$

et la condition initiale

\[\begin{split}Y(t=0) = \begin{pmatrix} x_0 \\ u_0 \end{pmatrix} \end{split}\]

8.1.2. 2nd étape: méthode numérique#

On calcule des valeurs approchées de \(Y(t)\) en se fixant un temps de simulation \(t_{fin}\), un pas en temps \(\Delta t\) tq. \(t_{fin} = (n-1) \Delta t\)

On calcule alors la solution approchée aux différents temps (au total \(n\) temps):

\[ T = \left[0, \Delta t, 2\Delta t, 3\Delta t, .... (n-1)\Delta t = t_{fin} \right]\]

Cette solution est stockée dans un vecteur \(\textbf{Y}\) de dimension \(n\):

\[ \textbf{Y} = \left[Y_0, Y_1, Y_2, Y_3, .... , Y_{n-1} \right]\]

On calcule les valeurs de \(\textbf{Y}\) de façon itérative, en utilisant un schéma de Runge Kutta:

  • à \(t=0\)

\[\begin{split} Y_0 = \begin{pmatrix} x_0 \\ u_0 \end{pmatrix} \end{split}\]

  • à \(t=t_k + \Delta t\) pour \(k=0\) à \(n-2\) ( méthode de RK 2)

\[ Y_{k+\frac{1}{2}} = Y_{k} + \frac{\Delta t}{2} \mathbf{F}\left(Y_{k}, t_k \right) \]
\[ Y_{k+1} = Y_{k} + \Delta t \mathbf{F}\left(Y_{k+\frac{1}{2}}, t_k + \frac{\Delta t}{2}\right)\]

8.1.3. 3ieme étape: Algorithme#

  • définition d’un fonction qui calcule \(\mathbf{F}(Y,t)\) où Y est un vecteur (dim t) et t une valeur scalaire

def Modele(Y,t):
    ...
    val = ...
    return val

  • définition d’un fonction qui itère la valeur numérique de \(\textbf{Y}\), i.e. calcule de \(Y_{k+1}\) en fonction de \(Y_k\)

def IterationRK2(Y,F,dt,t):
    """ Y:Yk, et on calcule Yk+1 , F:fonction second membre, dt:pas en temps, t:temps = kdt""
    Ymilieu = Y + 0.5*dt*F(Y,t)
    Ysuiv   = Y +     dt*F(Ymilieu, t+dt/2)
    return Ysuiv

  • itération de calcul: les variables dt, tfin, N et \(Y_0\) sont définies

dim = (N,2)      
Y_sol = np.zeros(dim)
Y_sol[0] = Y0
for k in range(N-1):
    Y_sol[k+1] = IterationRK2(Y_sol[k], Modele, dt, T[k])

8.2. Comportement d’une EDO du 2nd ordre#

système masse-ressort + amortissement

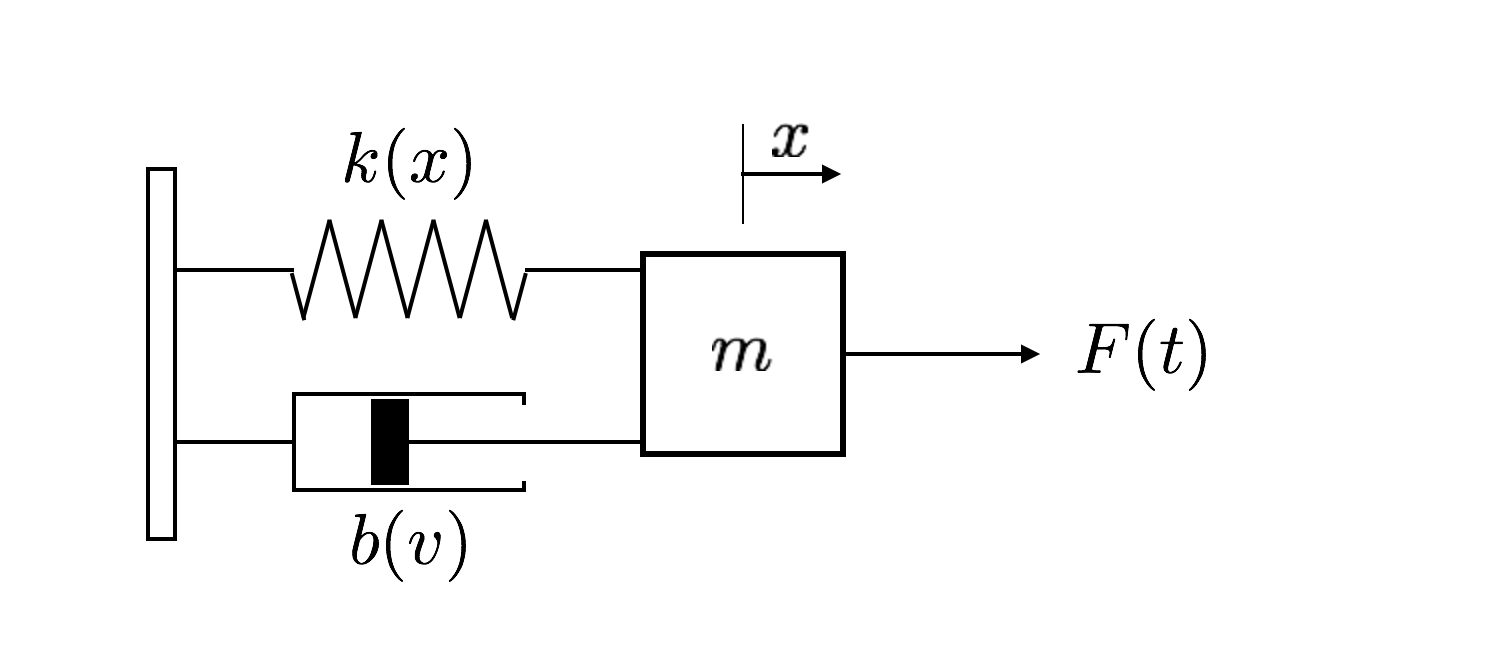
damped-spring.png

8.2.1. cas sans forcage \(f(t)=0\)#

Equation du mouvement

\[ \ddot{x} + 2\lambda_0 \dot{x} + \omega_0^2 x = 0 \]
from sympy import Derivative, Eq, dsolve
t = sp.symbols('t')
y = sp.symbols('y',cls=sp.Function)
lambda0, omega0 = sp.symbols("lambda_0 omega_0")
eq0 = Derivative(y(t),t,t) + 2*lambda0*Derivative(y(t),t) + omega0**2*y(t)
display("EDO ",eq0)

'EDO '
\[\displaystyle 2 \lambda_{0} \frac{d}{d t} y{\left(t \right)} + \omega_{0}^{2} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)}\]

8.2.2. différents mouvements possibles suivant \(\lambda_0\) (pour \(\omega_0=1\))#

  • fonction du signe de \(\Delta = \lambda_0^2 - omega_0^2\)

    • racines imaginaire pures

    • racines complexes

    • racines doubles

    • racines réelles

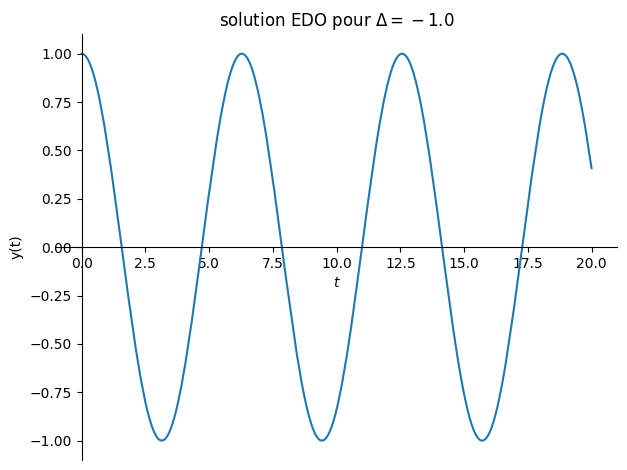
# cas sans amortissement: 
Valnum={lambda0:0,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'
\[\displaystyle y{\left(t \right)} = \cos{\left(t \right)}\]
../../_images/b6a0531f57d3176392bb7226860571135cb5912f3540a8f9a7d5297e0e7bd876.png 
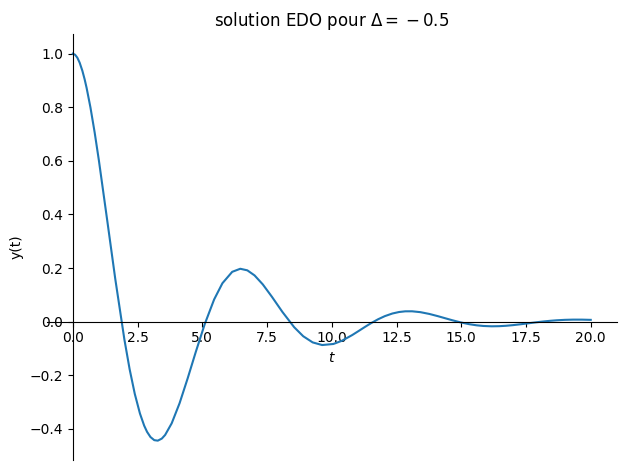
# pseudo periodique amortie
Valnum={lambda0:1/sp.S(4),omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'
\[\displaystyle y{\left(t \right)} = \left(\frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{15} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}}\]
../../_images/52c75f82673451d10d7488a9779755ebaf80eb0b1d7b1e856e192d8745e44285.png 
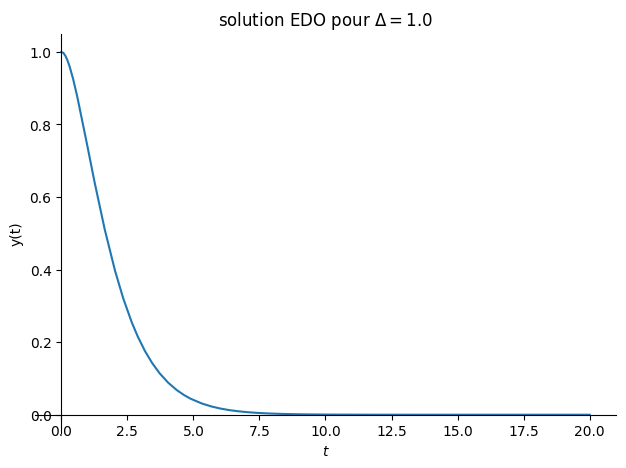
# critique
Valnum={lambda0:1,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'
\[\displaystyle y{\left(t \right)} = \left(t + 1\right) e^{- t}\]
../../_images/a12b16d8aa3691a16839fcc267da0f88e4a328fb5eadf3112f0c9ade0f71c967.png 
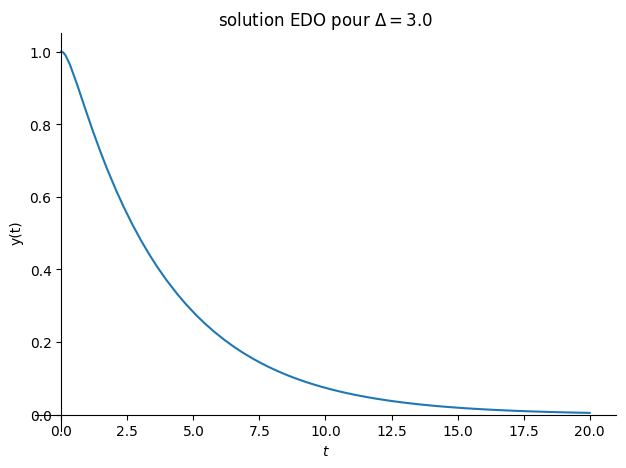
# amortie
Valnum={lambda0:2,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'
\[\displaystyle y{\left(t \right)} = \left(\frac{1}{2} + \frac{\sqrt{3}}{3}\right) e^{t \left(-2 + \sqrt{3}\right)} + \left(\frac{1}{2} - \frac{\sqrt{3}}{3}\right) e^{- t \left(\sqrt{3} + 2\right)}\]
../../_images/5bd60b858f2a1a71d1987630e4f711bb28bb595b84ff0befa4e48640e082c1fb.png

8.2.3. cas avec forçage \(f(t)\) mais sans amortissement#

\[ \ddot{y} + \omega_0^2 y = f(t)\]

  • solution = solution équation homogène + solution particulière

  • si forçage harmonique \(f(t)= A \cos(\omega_1 t)\)

  • la solution dépend de la valeur de \(\omega_1\) par rapport à \(\omega_0\)

    • si \(\omega_1 \neq \omega_0\) solution particulière \( y(t) = \alpha \cos{\omega_1 t}\)

    • si \(\omega_1 = \omega_0\) résonnance: solution particulière \( y(t) = t \sin{\omega_0 t}\)

omega1, A = sp.symbols("omega_1 A")
eq1 = Eq(Derivative(y(t),t,t) + omega0**2*y(t),A*sp.cos(omega1*t))
display("EDO ",eq1)

'EDO '
\[\displaystyle \omega_{0}^{2} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = A \cos{\left(\omega_{1} t \right)}\]

8.2.4. différents mouvements possibles fonctions de \(\omega_1\)#

On fixe \(\omega_0=1\)

  • étude fct de \(\omega_1\)

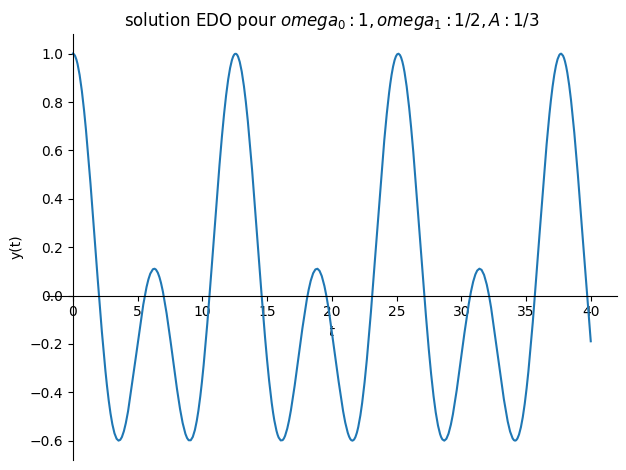
# avec forcage < omega
Valnum={omega0:1,omega1:1/sp.S(2),A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '
\[\displaystyle y{\left(t \right)} = \frac{4 \cos{\left(\frac{t}{2} \right)}}{9} + \frac{5 \cos{\left(t \right)}}{9}\]
../../_images/84c52d6a16377240814608c01e9a07d11f473f9b22584abe7ba5f2ff0634db45.png 
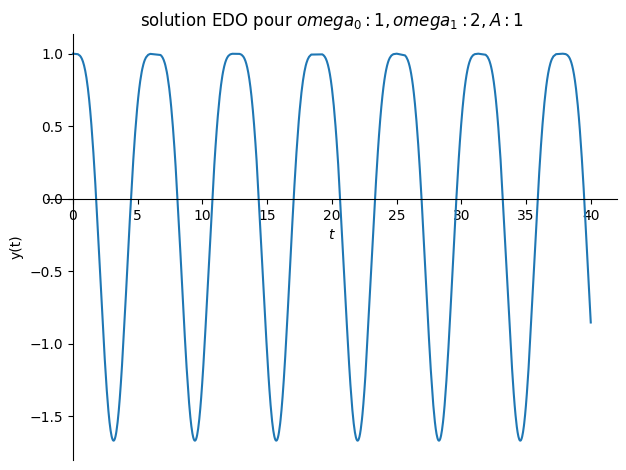
# avec forcage > omega
Valnum={omega0:1,omega1:sp.S(2),A:1}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '
\[\displaystyle y{\left(t \right)} = \frac{4 \cos{\left(t \right)}}{3} - \frac{\cos{\left(2 t \right)}}{3}\]
../../_images/66b33421abf2e65be1421f29ee43ad3025bc039239118cbd0cdcfe310e9065a5.png 
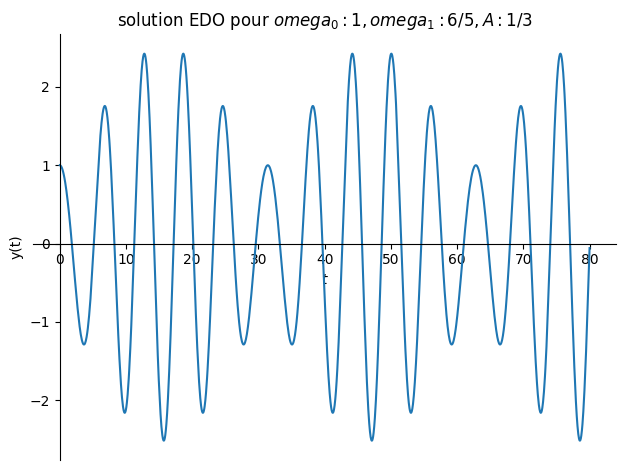
# avec forcage proche de omeg0
Valnum={omega0:1,omega1:6/sp.S(5),A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,80),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '
\[\displaystyle y{\left(t \right)} = \frac{58 \cos{\left(t \right)}}{33} - \frac{25 \cos{\left(\frac{6 t}{5} \right)}}{33}\]
../../_images/eb49aa369022ac63d11e35bde3da84fb1262d774ee169dc872e6e535bad9fc91.png 
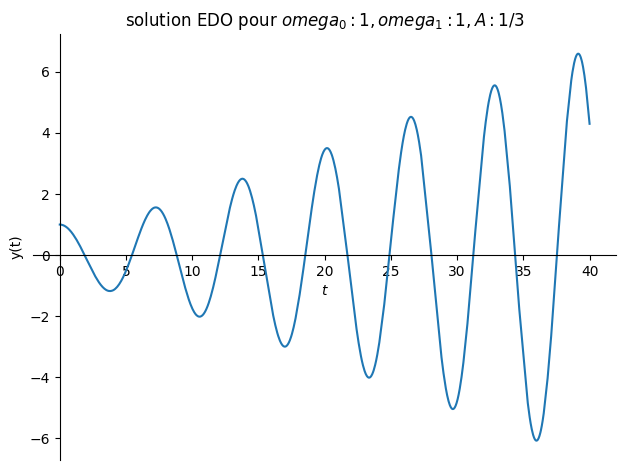
# resonnance omega1=omega0
Valnum={omega0:1,omega1:1,A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '
\[\displaystyle y{\left(t \right)} = \frac{t \sin{\left(t \right)}}{6} + \cos{\left(t \right)}\]
../../_images/5f2d3c1619bfefbaee10b64264896ea39cc9d98544e3064089bfe10bb4dbcc22.png

8.2.5. cas avec forçage \(f(t)\) et amortissement#

\[ \ddot{y} + 2\lambda_0 \dot{y} + \omega_0^2 y = f(t)\]

  • solution = solution équation homogène + solution particulière

omega1, A = sp.symbols("omega_1 A")
eq = Eq(Derivative(y(t),t,t) + 2*lambda0*Derivative(y(t),t) + omega0**2*y(t),A*sp.cos(omega1*t))
display("EDO ",eq)

'EDO '
\[\displaystyle 2 \lambda_{0} \frac{d}{d t} y{\left(t \right)} + \omega_{0}^{2} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = A \cos{\left(\omega_{1} t \right)}\]
# 
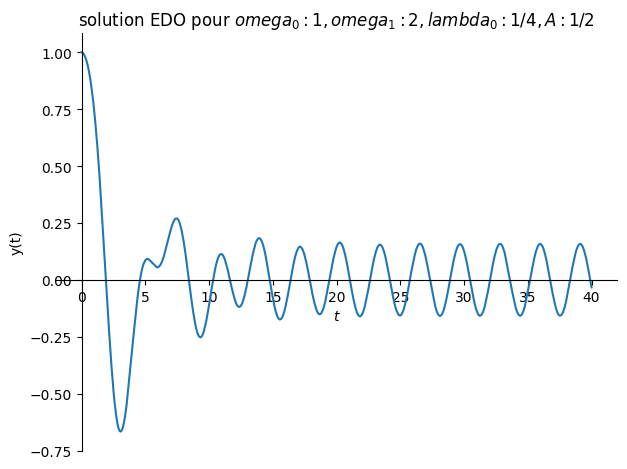
Valnum={omega0:1,omega1:4/sp.S(2),lambda0:1/sp.S(4),A:1/sp.S(2)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");
\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \frac{\cos{\left(2 t \right)}}{2}\]
'solution: '
\[\displaystyle y{\left(t \right)} = \left(\frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{20} + \frac{23 \cos{\left(\frac{\sqrt{15} t}{4} \right)}}{20}\right) e^{- \frac{t}{4}} + \frac{\sin{\left(2 t \right)}}{20} - \frac{3 \cos{\left(2 t \right)}}{20}\]
../../_images/46541078c47c00fc92903dbb580797ff318a78fd1c9f8603d1d95cf83bf55020.png 
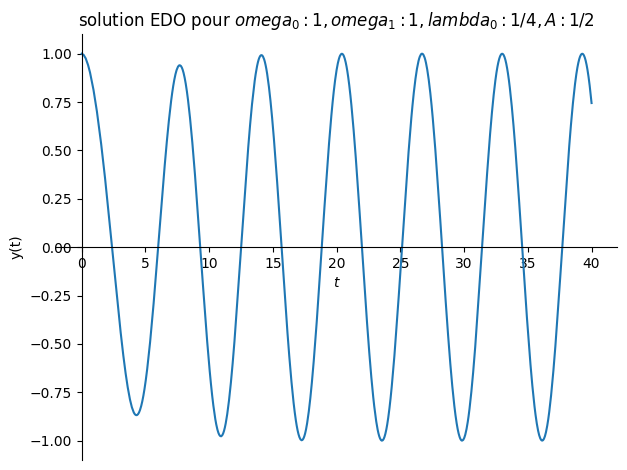
# resonnance
Valnum={omega0:1,omega1:2/sp.S(2),lambda0:1/sp.S(4),A:1/sp.S(2)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");
\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \frac{\cos{\left(t \right)}}{2}\]
'solution: '
\[\displaystyle y{\left(t \right)} = \left(- \frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{5} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}} + \sin{\left(t \right)}\]
../../_images/84dce08af4a0bef4fde4d956123ba0f784f2c3865ef1019208636b77771c80c2.png

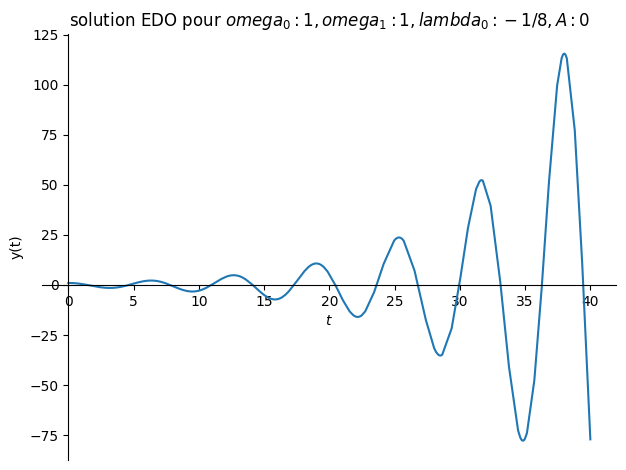
8.2.6. cas particulier \(\lambda_0 < 0 \)#

# resonnance
Valnum={omega0:1,omega1:2/sp.S(2),lambda0:-1/sp.S(8),A:0/sp.S(2)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");
\[\displaystyle y{\left(t \right)} - \frac{\frac{d}{d t} y{\left(t \right)}}{4} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = 0\]
'solution: '
\[\displaystyle y{\left(t \right)} = \left(- \frac{\sqrt{7} \sin{\left(\frac{3 \sqrt{7} t}{8} \right)}}{21} + \cos{\left(\frac{3 \sqrt{7} t}{8} \right)}\right) e^{\frac{t}{8}}\]
../../_images/6da76281e1c1fa24de0acbd5e167a8ec8032c37ff216d30eba3204927ada0381.png

8.3. Analyse du mouvement dans l’espace des phases#

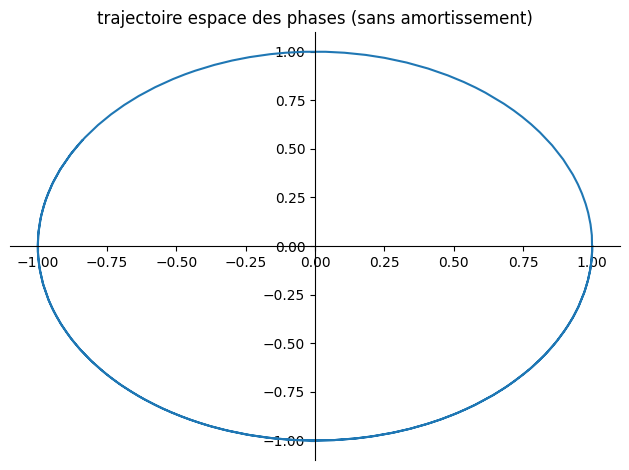
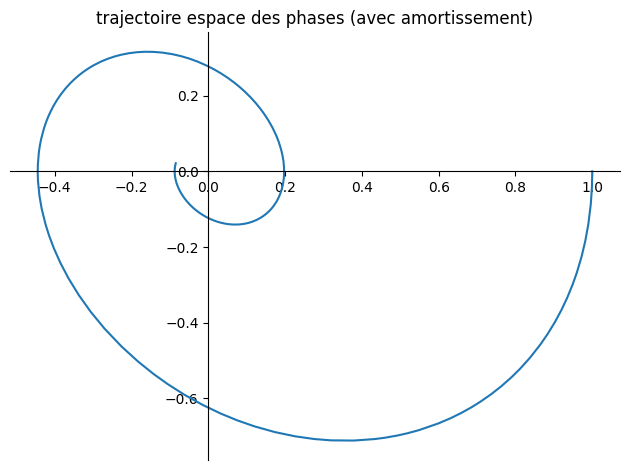
Le système masse-ressort peut se comporter de différentes manières. Si le ressort est linéaire et qu’il n’y a pas d’amortissement ou de forçage , le mouvement est périodique. Si nous ajoutons de l’amortissement, le mouvement oscillatoire décroît avec le temps. Avec le forçage, le mouvement peut être un peu plus compliqué et parfois présenter une résonance.

Chacun de ces types de mouvement est représenté par des solutions correspondantes au système différentiel, dictées par les paramètres du modèle et les conditions initiales.

Comment avoir une idée de tous les types de solutions à un système différentiel? Une méthode puissante pour ce faire est d’utiliser le plan de phase.

Un système de deux équations différentielles du premier ordre:

\[\begin{split} \mathbf{Y} = \mathbf{F}(Y,t) \mbox{ soit } \begin{eqnarray} \dot{y_1}(t) &=& f_1(y_1, y_2) \\ \dot{y_2}(t) &=& f_2(y_1, y_2) \end{eqnarray} \end{split}\]

avec un vecteur d’état

(8.1)#\[\begin{equation} \mathbf{Y(t)} = \begin{bmatrix} y_1(t) \\ y_2(t) \end{bmatrix}, \end{equation}\]

est appelé un système autonome planaire: planaire, car le vecteur d’état a deux composantes; et autonome (auto-génératrice), car la variable de temps n’apparaît pas explicitement sur le côté droit (qui ne s’appliquerait pas au système masse-ressort entraîné).

Pour les conditions initiales données \(\mathbf{Y}(0)=Y_0\), le système a une solution unique. Cette solution peut être représentée par une courbe plane sur le plan 𝑥𝑦 le plan de phase et est appelée une trajectoire du système. C’est une courbe paramétrique fonction de t.

8.3.1. cas sans forcage#

# cas sans amortissement: 
Valnum={lambda0:0,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution:",sol)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,10),title="trajectoire espace des phases (sans amortissement)")

'solution:'
\[\displaystyle y{\left(t \right)} = \cos{\left(t \right)}\]
../../_images/5e6474279b9139136bf1e14096e611271e989f3ba9ce5c5f146035532b7d88b9.png 
<sympy.plotting.plot.Plot at 0x7f153b3672e0>

Valnum={lambda0:1/sp.S(4),omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,10),title="trajectoire espace des phases (avec amortissement)")

'solution :'
\[\displaystyle y{\left(t \right)} = \left(\frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{15} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}}\]
../../_images/51be22c1ca25a9b4a2b1892936015899c5e3f57fa355bc0188bc96e4f4f3a9bd.png 
<sympy.plotting.plot.Plot at 0x7f153b23f640>

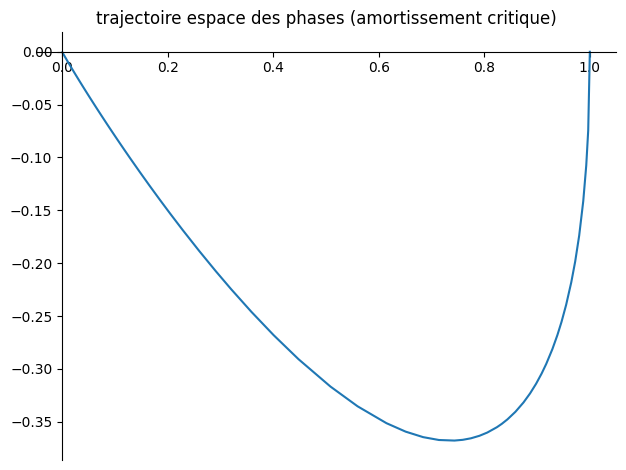
# critique
Valnum={lambda0:1,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,10),title="trajectoire espace des phases (amortissement critique)")

'solution :'
\[\displaystyle y{\left(t \right)} = \left(t + 1\right) e^{- t}\]
../../_images/b15f807c6670ade9ce7b5ba61d84e4378508b6d4a1ca68a0da627cbeea991ed7.png 
<sympy.plotting.plot.Plot at 0x7f153b2966e0>

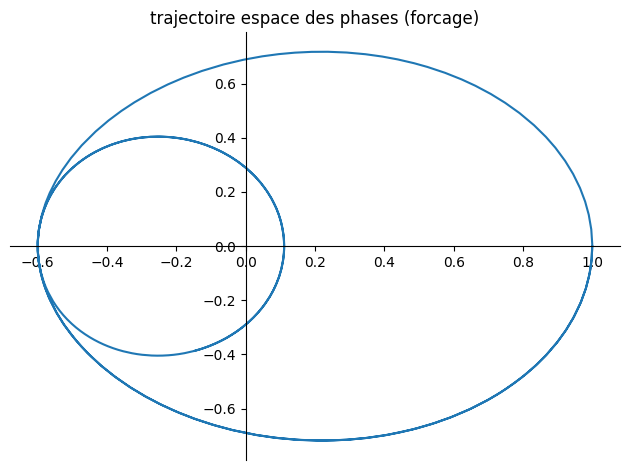
8.3.2. cas avec forcage (sans amortissement)#

# avec forcage < omega
Valnum={omega0:1,omega1:1/sp.S(2),A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,20),title="trajectoire espace des phases (forcage)")

'solution: '
\[\displaystyle y{\left(t \right)} = \frac{4 \cos{\left(\frac{t}{2} \right)}}{9} + \frac{5 \cos{\left(t \right)}}{9}\]
../../_images/ff393dd6a7b692086272b3256faaebdb9edd792584cfeb61cf854cb2712c14de.png 
<sympy.plotting.plot.Plot at 0x7f153b4d45e0>

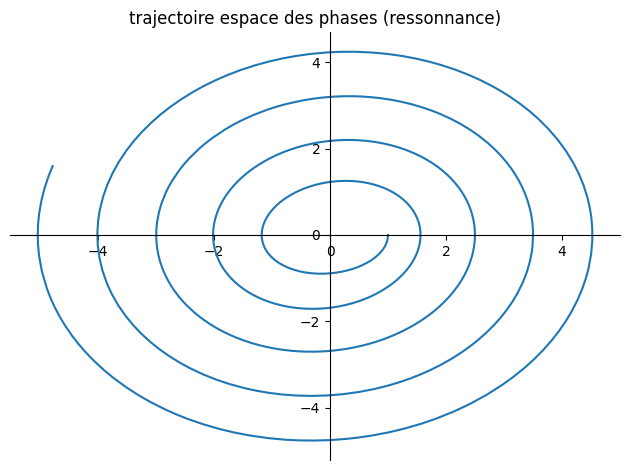
# resonnance omega1=omega0
Valnum={omega0:1,omega1:1,A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,30),title="trajectoire espace des phases (ressonnance)")

'solution: '
\[\displaystyle y{\left(t \right)} = \frac{t \sin{\left(t \right)}}{6} + \cos{\left(t \right)}\]
../../_images/33f70d005bd4556bafc205983b7ddf0990a77aab1b2003ddaf5a4aa27ea4f4b2.png 
<sympy.plotting.plot.Plot at 0x7f153996ac80>

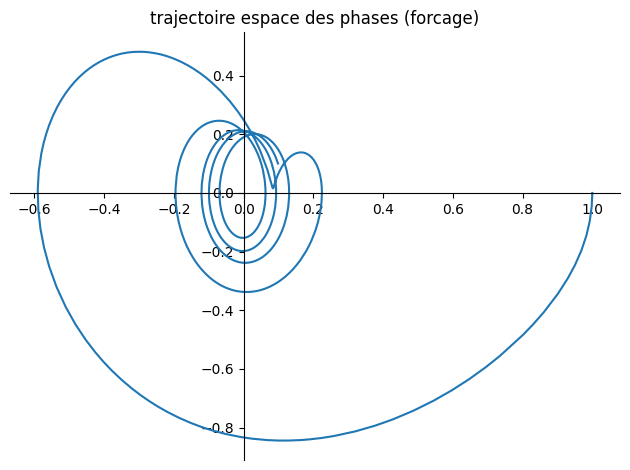
8.3.3. cas général#

# 
Valnum={omega0:1,omega1:4/sp.S(2),lambda0:1/sp.S(4),A:1/sp.S(3)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,20),title="trajectoire espace des phases (forcage)")
\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \frac{\cos{\left(2 t \right)}}{3}\]
../../_images/44318a744a480354d0aec88f2f76e87df900b76797c9bce9843c49871c8c8631.png 
<sympy.plotting.plot.Plot at 0x7f153b607790>

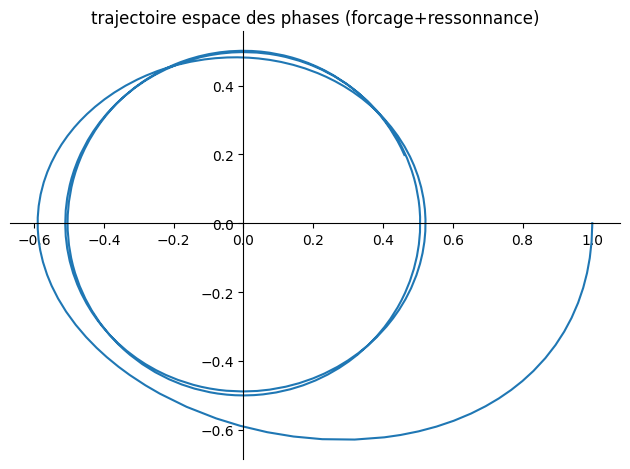
# resonnance
Valnum={omega0:1,omega1:2/sp.S(2),lambda0:1/sp.S(4),A:1/sp.S(4)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
y1 = sol.rhs
y2 = y1.diff(t)
plot_parametric((y1,y2),(t,0,20),title="trajectoire espace des phases (forcage+ressonnance)")
\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \frac{\cos{\left(t \right)}}{4}\]
'solution: '
\[\displaystyle y{\left(t \right)} = \left(- \frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{15} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}} + \frac{\sin{\left(t \right)}}{2}\]
../../_images/493c59c63f3bcce58f63e7532297852301b001180807b08fd5ca663970861a66.png 
<sympy.plotting.plot.Plot at 0x7f153b5113c0>

8.4. FIN de la leçon#

Contenu