Modèlisation du brachistochrone

13. Modèlisation du brachistochrone#

brachistochrone

Marc Buffat département mécanique Lyon 1

# bibliotheque mecanique
import numpy as np
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum,cross
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
from validation.validation import info_etudiant, bib_validation
from validation.valide_markdown import test_markdown, test_code
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_  = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("## Etudiant {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
bib_validation('cours','MGC2028L')

13.1. Objectif#

L’objectif de ce TP est d’apporter un complément à l’étude expérimentale du TP précédent, en proposant une approche complémentaire pour le résoudre avec:

  1. un modèle théorique analytique dans le cas simple du roulement d’une bille sur un plan incliné en utilisant du calcul formel

  2. un modèle numérique pour résoudre le problème dans le cas général

Remarque : la partie numérique peut etre traitée sans avoir terminé la partie analytique

13.2. 1er modèle: bille sur un plan incliné#

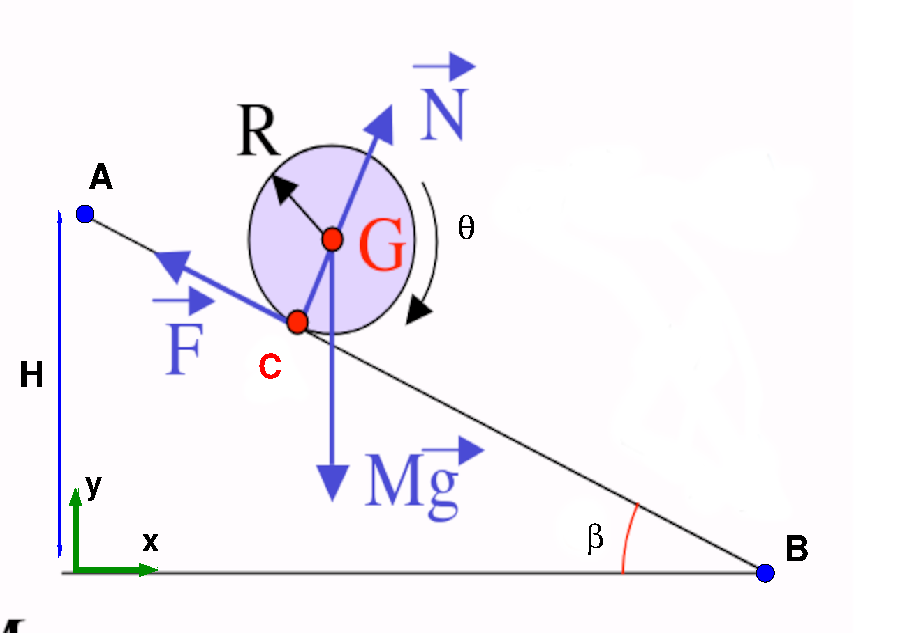
bille_plan

  • on définit un repère fixe R0 (x,y,z)

  • la trajectoire de la bille est la droite A,B de hauteur H et d’angle \(\beta\)

  • la bille est une sphère homogène de rayon R et de masse M

Dans cette partie, on utilisera exclusivement la bibliothèque sympy de calcul symbolique (noté sp), donc toutes les fonctions mathématiques devront être précédées de sp:

  • sp.cos sp.sin sp.tan…..

On utilisera aussi des fonctions de classe (méthode) associées aux variables de cette bibliothèque sous la forme:

  • var.fonction()

attention pour les calculs analytiques simples, vous pouvez mettre directement la solution analytique sans forcement utiliser les fonctions sympy : sp.solve(eq,var) ou .subs()

13.2.1. paramètres et ddl#

On définit dans la cellule suivante:

  • les paramètres du problème: R,M,\(\beta\) et H

  • les 2 degrés de liberté \(x(t)\) (position en x du centre de gravité G) et \(\theta(t)\) (angle de rotation de la bille autour de z)

  • la position verticale \(y(t)\) de la bille est fixée par la forme de la trajectoire $\( y(t) = - \tan\beta\; x(t)\)$

# parametres du problème: rayon, masse , beta, hauteur   
R, M, beta,H = sp.symbols('R M beta H')
t = sp.symbols('t')
# degrés de liberté angle et position de G (x,y)
theta, x  = dynamicsymbols('theta x')
y = -sp.tan(beta)*x

13.2.2. définition des repères et des points#

On définit ensuite

  • le référentiel fixe:

    • origine: point O tq à t=0 le centre de gravité de la bille coïncide avec O

    • repère cartésien R0

  • le référentiel lié à la bille

    • G: le centre de gravité de la bille

    • repère cartésien R1 en rotation \(\theta\) autour de z

  • un point P quelconque sur la surface de la bille $\(\vec{GP} = R \vec{e_1}_x\)$

# reperes et points
O = Point('O')
R0 = ReferenceFrame('R_0')
# centre de la bille G
G = Point('G')
G.set_pos(O,x*R0.x+y*R0.y)
display("OG=",G.pos_from(O).express(R0))
# bille 
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[theta, R0.z])
# point P sur le rayon
P = Point('P')
P.set_pos(G,R*R1.x)
display("OP=",P.pos_from(O).express(R0))

13.3. définition de points suppémentaires#

  • définir le vecteur tangent et normal au point de contact dans les variables T et N (la tangente est orientée dans le sens du mouvement de la bille) dans le repère R0.

  • définir la position des 2 points A et B, point de contact de la bille au début et à la fin du problème en fonction des paramètres en utilisant la fonction .set_pos

  • en déduire la position du point de contact C

A = Point('A')
B = Point('B')
C = Point('C')
T = 0
N = 0
## BEGIN SOLUTION
# tangente et normale au point de contact C 
# A et B point de contact de la bille au debut et à la fin
#A.set_pos(O,-R*R0.y)
#B.set_pos(O,-(H+R)*R0.y + H/sp.tan(beta)*R0.x)
# Point de contact C
## END SOLUTION

display("OA:",A.pos_from(O).express(R0))
display("OB:",B.pos_from(O).express(R0))
display("OC:",C.pos_from(O).express(R0))
assert(T.dot(N) == 0)
assert((T.cross(N)).dot(R0.z).trigsimp()==1)
assert(B.pos_from(A).dot(B.pos_from(A)).trigsimp() == (H/sp.sin(beta))**2)
assert(G.pos_from(C).dot(N).trigsimp() == R)

13.3.1. définition du solide bille#

pour définir le solide bille on donne

  • sa matrice d’intertie IG, qui est diagonale dans le repère R1

  • son centre de gravité G, sa masse M , un repère lié à la bille R1

I1 = 2*M*R**2/5
IG = inertia(R1,I1,I1,I1)
display("matrice inertie:",IG)
bille = RigidBody('Bille',G,R1,M,(IG,G))

13.3.2. calcul de la vitesse de G#

On fixe la vitesse de O à 0.

En dérivant la position du point G \(\vec{OG}\) par rapport à R0 (avec la méthode G.pos_from()et .diff(t,repère) ) calculer la vitesse de G dans la variable VG et affectée sa valeur au point G en utilisant la méthode G.set_vel(repere, valeur)

# calcul vitesse
O.set_vel(R0,0)
VG = 0
## BEGIN SOLUTION
## END SOLUTION

display("VG=",G.vel(R0))
assert(G.vel(R0).dot(G.vel(R0)).trigsimp() == (x.diff(t)/sp.cos(beta))**2)

13.3.3. condition de roulement sans glissement#

La condition de roulement sans glissement de la bille sur le plan impose que la vitesse de la bille au point de contact C doit être nulle.

En appliquant la composition de mouvement pour un point P de la bille $\( \vec{V}_{P/R_0} = \vec{V}_{G/R_0} + \vec{V}_{P/R_1}\)\( calculer la vitesse de ce point en C en notant que dans ce cas la vitesse relative \)\vec{V}_{P=C/R_1}\( s'écrit simplement en fonction de \)\dot{\theta}\( et de la distance \)\vec{GC}$.

On mettra le résultat dans la variable VC

En écrivant que cette vitesse doit etre nulle, en déduire la condition de roulement sans glissement reliant \(\dot{x}\) et \(\dot{\theta}\), i.e. x.diff(t) et theta.diff(t)

On écrira cette condition dans la variable cds sous la forme d’un dictionnaire

  cds = { x.diff(t) : expression en fonction de theta.diff(t) }

VC  = 0
cds = {}
## BEGIN SOLUTION
# vitesse en C point de contact = 0
# ou
# cdts de roulement sans glissement (on peut aussi écrire directement)
# ou explicitement
# cds = {x.diff(t):-R*sp.cos(beta)*theta.diff(t)}
# remarque dtheta < 0 
## END SOLUTION

display("VC=",VC)
display("cds=",cds)
assert(VC.dot(VC).simplify() - ((R*theta.diff(t)+x.diff(t)/sp.cos(beta))**2).expand() == 0)
assert(VC.subs(cds).simplify() == 0 )

13.3.4. Calcul de la quantité de mouvement et du moment cinétique en C#

en utilisant les méthodes bille.linear_momentum() et bille.angular_momentum(), calculer la quantité de mouvement et le moment cinétique en C de la bille.

On mettra le résultat respectivement dans les variables Qmvt et Mc. On simplifiera le résultat du moment cinétique Mc avec la condition de roulement sans glissement en utilisant la méthode de substitution .subs(cds) et la méthode de simplification .simplify(). Le résultat sera exprimé dans R0 avec la méthode .express

Qmvt = 0
Mc = 0
## BEGIN SOLUTION
# qte mouvement et moment cinetique
# avec les cdts de non glissement
## END SOLUTION

display("qte mvt     :",Qmvt)
display("mt cinétique en C:",Mc)
assert(Qmvt.dot(Qmvt).trigsimp() == (M*x.diff(t)/sp.cos(beta))**2)
assert((Mc.dot(R0.z)/theta.diff(t)).diff(t) == 0 )

13.3.5. Equations du mouvement#

En notant \(R_t\) et \(R_n\) les composantes de la force de contact \(\vec{F}_c\) en C suivant la tangente et la normale:

\[\vec{F}_c = R_t \vec{t} + R_n \vec{n} \]

on peut définir les forces appliquées;

On justifiera dans le compte rendu que le principe fondamentale de la dynamique permet de calculer la variation du moment cinétique en C en fonction uniquement du moment du poids:

\[ \frac{d}{dt} \vec{\sigma}_C = \vec{CG} \wedge M \vec{g} \]

On écrira cette équation sous la forme:

\[ \mbox{eq2=} \frac{d}{dt} \vec{\sigma}_C - \vec{CG} \wedge M \vec{g} \]

qui sera traduit par la condition \(eq2 = 0\)

Le résultat est mis dans la variable eq2

# bilan des Force gravité et reaction (force contact) de composante normale Rn et tangentielle Rt
g, Rt, Rn  = sp.symbols('g R_t R_n')
Poids = - M*g*R0.y
Fc = Rt*T + Rn*N
# variation du moment cinétique en C (Mt des forces en C)
eq2 = Mc.diff(t,R0) - cross(G.pos_from(C),Poids)
eq2 = eq2.express(R0)
display(eq2)

13.3.6. Solution analytique#

En déduire à partir de cette équation la valeur de \(\ddot{\theta}\) sous la forme \(\ddot{\theta} = val_2 \) que l’on écrira avec sympy sous la forme d’une équation

  sol2 = sp.Eq(theta.diff(t,t) , val2)
  display(sol2)

En déduire la solution du problème \(\theta(t)\) en fonction de \(t\) en utilisant la condition initiale: $\(\theta(0)=\dot{\theta}(0)=0\)$ que l’on écrira avec sympy sous la forme d’une équation:

  sol1 = sp.Eq(theta, val1)
  display(sol1)

En utilisant la condition de roulement sans glissement, en déduire la valeur de solution \(x(t)\) que l’on écrira avec sympy sous la forme d’une équation:

  sol0 = sp.Eq(x, val0)
  display(sol0)

En déduire la valeur du coefficient \(K\) théorique du TP précédent dans la variable Kth

Commenter ce résultat

sol2 = 0
sol1 = 0
sol0 = 0
Kth = 0
## BEGIN SOLUTION
# on peut aussi écrire directement l'expression sans solve
# sol2 = sp.Eq(theta.diff(t,t),-5*g*sp.sin(eta)/(7*R))
# ou directement 
## END SOLUTION

display(sol2)
display(sol1)
display(sol0)
display("Kth=",Kth)
assert((sol0.rhs/R + sol1.rhs*sp.cos(beta)).simplify() == 0)
assert((sol2.rhs*R/(-g*Kth*sp.sin(beta))).simplify() == 2)

13.3.7. Bilan d’énergie#

Expliquez dans le compte rendu pourquoi le système étudié est conservatif.

  1. Calculer l’énergie cinétique Ec en utilisant la méthode .kinetic_energy() en la simplifiant.

  2. Calculer l’énergie potentielle Up en fonction du poids et de y en choisissant qu’à l’instant initial l’énergie potentielle est nulle.

  3. Calculer l’énergie totale du système dans la variable Et en fonction de l’énergie cinétique Ec et de l’énergie potentielle Up.

Compte tenu des conditions initiales: $\(\theta(0) = \dot{\theta}(0) = x(0) = \dot{x}(0) = y(0) = \dot{y}(0) = 0\)$ quelle est la valeur (très simple) de l’énergie totale ?

En déduire une équation donnant \(\dot{\theta(t)}\) en fonction de \(x(t)\) que l’on écrira avec sympy sous la forme d’une équation:

  sol4 = sp.Eq(theta.diff(t), val4)
  display(sol4)

On justifiera le choix du signe de \(\dot{\theta}\)

Ec = 0
Up = 0
Et = 0
sol4 = 0
## BEGIN SOLUTION
# one peut aussi directement écrire le résultat sans solve
# sol4 = -sp.Eq(theta.diff(t),sp.sqrt(10*g*x*sp.tan(beta)/7)/R)
## END SOLUTION

bille.kinetic_energy(R0)

display("Ec:",Ec)
display("Ep:",Up)
display("Et:",Et)
display(sol4)
assert((Et.subs(theta.diff(t),sol4.rhs)).simplify() == 0)

13.4. Cas général: roulement sur une courbe quelconque#

Pour le cas général, on écrit la relation entre \(x(t)\) et \(y(t)\) sous la forme: \(y=f(x)\)

On va utiliser l’équation de conservation de l’énergie et la condition de roulement sans glissement pour obtenir 2 équations donnant respectivement \(\dot{\theta}\) et \(\dot{x}\), en fonction de \(x\) et de \(f(x)\) que l’on résoudra ensuite numériquement.

f = sp.Function('f')
y = f(x)

13.4.1. Calcul de la tangente et la normale#

au point de contact C on peut calculer la tangente \(\vec{t}\) et la normale \(\vec{n}\) à la courbe en fonction de \(f(x)\) et de \(\frac{df}{dx}\) (on donnera une explication dans le compte rendu)

\[\begin{split} \vec{t} = \begin{bmatrix} \frac{1}{\sqrt{1 + \frac{df}{dx}^2}}\\ \frac{\frac{df}{dx}}{\sqrt{1 + \frac{df}{dx}^2}} \end{bmatrix} \mbox{ et }\vec{n} = \begin{bmatrix} \frac{-\frac{df}{dx}}{\sqrt{1 + \frac{df}{dx}^2}}\\ \frac{1}{\sqrt{1 + \frac{df}{dx}^2}} \end{bmatrix} \end{split}\]
# tangente et normale au point de contact C (tangente à la courbe y=f(x))
T = (R0.x + y.diff(x)*R0.y)/sp.sqrt(1+y.diff(x)**2)
N = (-y.diff(x)*R0.x + R0.y)/sp.sqrt(1+y.diff(x)**2)
display(T,N)
print("verification:",T.dot(N) , T.cross(N).simplify().dot(R0.z))

13.4.2. Condition de roulement sans glissement en C#

en utilisant la même approche que précédemment, calculer la position de G en fonction de \(x\) et \(f\), puis la vitesse de G dans la variable VG. On modifiera aussi la vitesse du point G avec la fonction G.set_vel()

En déduire la vitesse au point de contact C dans la variable VC et enfin la condition de roulement sans glissement dans la variable sol6 sous la forme d’une équation \(\dot{x} = expression\) écrire en Python avec sp.Eq()

    sol6 = sp.Eq(x.diff(t), expression)

# cdts de roulement sans glissement
# vitesse en C point de contact = 0
VG = 0
VC = 0
sol6 = 0
## BEGIN SOLUTION
# ou
# ou + simple
## END SOLUTION

display("VG=",VG)
display("VC=",VC)
display(sol6)
assert((VC.dot(R0.x).subs(x.diff(t),sol6.rhs)==0) and (VC.dot(R0.x).subs(x.diff(t),sol6.rhs)==0))

13.4.3. Conservation de l’énergie#

On calcule l’énergie totale du système dans la variable Et en fonction de l’énergie cinétique Ec et de l’énergie potentielle Up.

Quelle est la valeur de l’énergie totale ?

En déduire une équation donnant \(\dot{\theta(t)}\) en fonction de \(x(t)\) que l’on écrira avec sympy sous la forme d’une équation:

  sol7 = sp.Eq(theta.diff(t), expression)
  display(sol7)

On justifiera le choix du signe de \(\dot{\theta}\)

Ec = bille.kinetic_energy(R0).subs(x.diff(t),sol6.rhs).simplify()
Up = -Poids.dot(y*R0.y)
Et = (Ec+Up).doit()
display("Et=",Et)

sol7 = 0
## BEGIN SOLUTION
# ou calcul directe
# sol7 = -sp.Eq(theta.diff(t),-sp.Eq(theta.diff(t),sp.sqrt(10*g*f(x)/7)/R)
## END SOLUTION

display(sol7)
assert(Et.subs(theta.diff(t),sol7.rhs) == 0 )

13.4.4. Equations du système#

A partir des 2 équations dans les variables sol6 et sol7 on en déduit les 2 équations à résoudre donnant \(\dot{\theta}\) et \(\dot{x}\) en fonction de \(x\) et \(f(x)\)

Quelle sont les conditions initiales associées ?

display(sol6.subs(theta.diff(t),sol7.rhs))
display(sol7)

13.5. Solution numérique#

On écrit le système précédent sous forme vectorielle en notant $\( Y = \begin{pmatrix} x \\ \theta \end{pmatrix} \)$

solution de l’EDO

\[\begin{split}\dot{Y} = \mathbf{F}(Y) \mbox{ avec } \mathbf{F}(Y) = \begin{pmatrix} \frac{\sqrt{-\frac{10}{7} g f(x)}}{\sqrt{1+ (\frac{df}{dx})^2}}\\ \frac{- \sqrt{-\frac{10}{7} g f(x)}}{ R}\\ \end{pmatrix}\end{split}\]

la trajectoire est fixée : $\(y=f(x) \mbox{ tq. } y(0)=0 \mbox{ et } y(x_1)=-H\)$

%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='18')
from brachisto import brachisto

bra = brachisto(_uid_)
printmd("## parametres: "+str(bra))

13.5.1. paramètres d’étude#

Les paramètres du cas étudié ainsi que les courbes de trajectoires sont donnés dans une variable braavec:

  • bra.x1 valeur numérique de x1

  • bra.H valeur numérique de H

  • bra.R valeur numérique de R

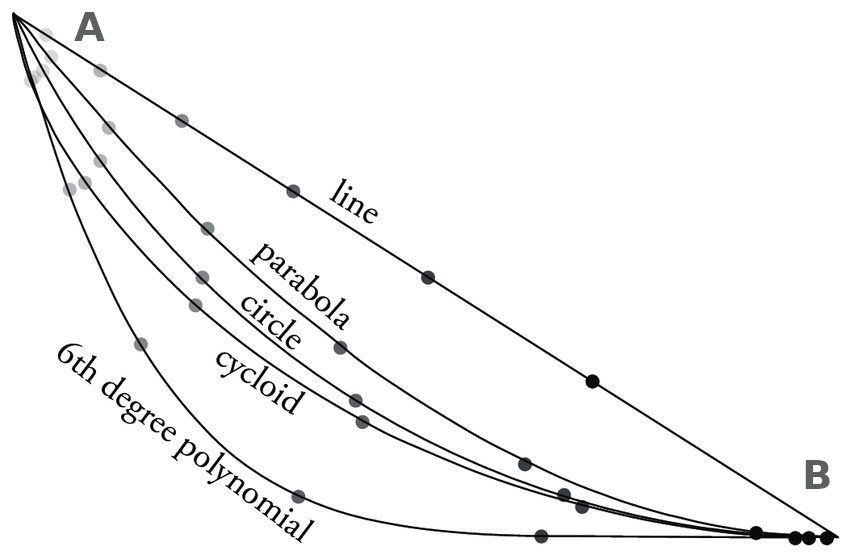
Les 5 trajectoires à étudier sont données par les 5 fonctions de x \(f(x)\) suivantes ainsi que leurs dérivées \(\frac{df }{dx}\)

  1. bra.f0() et bra.df0()

  2. bra.f1() et bra.df1()

  3. bra.f2() et bra.df2()

  4. bra.f3() et bra.df3()

  5. bra.f4() et bra.df4()

dans la cellule suivante tracer les 5 trajectoires à étudier sur une même courbe

# tracer des 5 trajectoires
## BEGIN SOLUTION
## END SOLUTION

assert(test_code("TP_model_brachistochrone.ipynb","cell-verif1",["plt.plot","plt.title","plt.legend(","xlabel("]))

13.5.2. modèle d’étude#

dans la cellule suivante, définir une fonction model(Y) qui calcule le second membre \(\mathbf{F}(Y)\) du système d’équations différentielles à résoudre

\[\begin{split}\dot{Y} = \mathbf{F}(Y) \mbox{ avec } \mathbf{F}(Y) = \begin{pmatrix} \frac{\sqrt{-\frac{10}{7} g f(x)}}{\sqrt{1+ (\frac{df}{dx})^2}}\\ \frac{- \sqrt{-\frac{10}{7} g f(x)}}{ R}\\ \end{pmatrix}\end{split}\]

$$

on définira des variables globales:

  • g=9.81

  • les paramètres du problème (données dans bra) R

  • la fonction f et sa dérivée df (en fonction de la courbe étudiée)

par exemple pour étudier la trajectoire 0, on écrit

  f = bra.f0
  df = bra.df0

g = 9.81
R = bra.R
H = bra.H
f = None
df = None
## BEGIN SOLUTION
#f = bra.f2
#df = bra.df2
#f = bra.f0
#df = bra.df0
## END SOLUTION

# test appel de la fonction
## BEGIN SOLUTION
## END SOLUTION

assert(test_code("TP_model_brachistochrone.ipynb","cell-verif2",["model("]))

Nous avons vu précédemment comment résoudre un problème d’EDO avec la méthode de RungeKutta d’ordre 2

Ecrire la fonction iterationRK2 pour le calcul de la solution numérique par RungeKutta 2 en notant que les EDO du problème traité ne dépendent pas explicitement du temps, donc la variable temps n’apparait pas dans les arguments.

       iterationRK2(Y, F, dt)

# iteration RK2
def iterationRK2(Yk,F,dt):
## BEGIN SOLUTION
## END SOLUTION

# test appel de la fonction
## BEGIN SOLUTION
## END SOLUTION

assert(test_code("TP_model_brachistochrone.ipynb","cell-verif3",["iterationRK2(","model"]))

13.5.3. simulation numérique#

On fixe le pas d’intégration dt à 1/1000e de seconde.

On ne connaît pas a priori le temps d’intégration, qui correspond au temps mis par la bille pour parcourir la trajectoire et qui est un des résultats attendus de la simulation.

La solution est de fixer a priori un temps de simulation tmax grand, et d’arrêter la simulation lorsque la bille arrive en bas de la trajectoire, c.a.d en B.

Pour cela il suffit d’ajouter dans la boucle de simulation un test if qui compare la position xk de la bille calculée à l’étape k avec la position de B, et d’arreter les itérations si xk>=x1.

Sous Python, l’instruction d’arret des itérations est break

   if xk >= x1 :
      break

Dans la cellule suivante, choisir un temps tmax de quelques secondes (2 à 3), en déduire un nombre maximum de pas de calcul dans N, le tableau T des pas en temps et le tableau sol_num de la solution numérique à calculer.

Effectuer la simulation en arrêtant la boucle lorsque la bille atteint B et en déduire le temps de parcours de la trajectoire dans tfin, l’indice de l’étape en temps dans kfin et la distance parcourue dans lfin

On pourra ajuster le temps tmax.

dt = 0.001
tmax = 0.
N = 0
T = None
sol_num = None
kfin = 0
tfin = 0.
lfin = 0.
## BEGIN SOLUTION
## END SOLUTION

print("tfin:{:.4}s, lfin {:.4}m ".format(tfin,lfin))
assert((kfin<N) and (tfin == T[kfin]) and (np.abs(H+f(sol_num[kfin,0]))<1.e-2))

13.5.4. tracé de la solution#

Tracer l’évolution de \(x(t)\) et \(\theta(t)\) en fonction du temps

# tracer
## BEGIN SOLUTION
## END SOLUTION

assert(test_code("TP_model_brachistochrone.ipynb","cell-verif4",["plt.plot","plt.title","plt.legend(","xlabel("]))

13.5.5. Analyse#

Refaire l’étude précédente pour les 5 courbes de l’étude en changeant la fonction f et df

Dans le compte rendu on regroupera dans un tableau les résultats sur tfin et Lfin donnant le temps de parcours et la longueur de la trajectoire (voir la syntaxe dans la document markdown (https://jupyterl2.mecanique.univ-lyon1.fr/cours_html/markdown.html)

courbe

tfin

lfin

0

xxx

xxx

que l’on analysera pour en tirer des conclusions. On pourra comparer le module de la vitesse finale de G avec la vitesse moyenne.

# optionnel tracer de la vitesse de G
### BEGIN SOLUTION
### END SOLUTION

13.6. Compte rendu#

Ecrire votre analyse et votre conclusion dans le compte rendu en insistant sur

  1. Description de la méthode d’analyse

  2. Résultat de l’analyse

  3. Conclusion

Le compte rendu est à écrire dans le fichier CompteRendu.md

  1. Génération de la version HTML du Compte Rendu (avec mise en page)

  • Exécution de la commande ci-dessous pour générer le fichier html

  1. Visualisation du Compte Rendu (version html)

  • Cliquez sur le lien suivant après exécution de la commande ci-dessous

  • Cliquez sur le bouton mise à jour du navigateur pour mettre à jour la page web

# génération de la version html du CR
!genereTPhtml CompteRendu

# test sur les commentaires (a executer)
assert(test_markdown('CompteRendu.md',None,minm=200,maxe=0.25))

14. FIN#
Contenu