7. Mouvements de Lagrange d’une toupie#
Marc Buffat département mécanique Lyon 1

7.1. Modélisation#
Pour définir la position de la toupie, on utilise les angles d’Euler.
7.1.1. angles d’Euler#
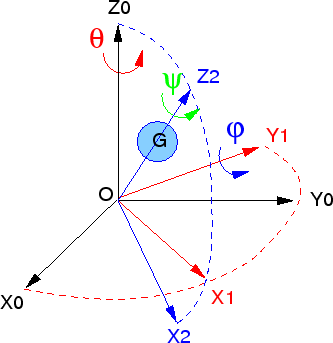
On étudie la cinématique 3D d’une toupie de rayon \(R\), en rotation autour son axe principal d’inertie (axe de révolution) avec un centre de gravité \(G\) distant de \(h\) de O: \(\overrightarrow{OG}=h\,\overrightarrow{Z_{2}}\). On suppose que le point O reste immobile.
Les 3 degrés de liberté du système sont les 3 angles d’Euler:
\(\theta(t)\) l’angle de précession de l’axe de la toupie autour de \(Z_{0}\)
\(\phi(t)\) l’angle de nutation (oscillation de l’axe autour de \(Y_{1}\))
\(\psi(t)\) l’angle de rotation propre de la toupie autour de son axe \(Z_{2}\)
%matplotlib inline
import numpy as np
import sympy as sp
import k3d
import matplotlib.pyplot as plt
# bibliotheque mecanique
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum
from sympy.physics.vector import Vector,time_derivative,dot
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
#
from IPython.display import display, Markdown, clear_output
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
from validation.validation import info_etudiant
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
#raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Etudiant {} {} id={}**".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_h = 2 + np.random.randint(8)
_R = 1 + np.random.randint(4)
_omega = 2 + np.random.randint(6)
_Omega = 5*_omega
_phi0 = np.random.randint(7)
_phip = _omega//2
printmd("Paramétres de la toupie: R={} cm h={}cm ".format(_R,_h))
ERREUR: numéro d’étudiant non spécifié!!!
Etudiant Marc BUFFAT id=137764122
Paramétres de la toupie: R=3 cm h=5cm
7.2. Modèle mécanique#
on définit les paramêtres du problème: le rayon \(R\) et la distance \(h\)
on définit les degrés de liberté: 3 ddl les 3 angles d’Euler \(\theta(t), \phi(t), \psi(t)\)
on définit les repères \(R_0, R_1, R_2, R_3\) et la position des points
7.2.1. paramètres du problème#
# parametres du problème: rayon distance
R,h,g,t = sp.symbols('R h g t')
# degrés de liberté
theta = dynamicsymbols('theta')
phi = dynamicsymbols('phi')
psi = dynamicsymbols('psi')
7.2.2. Repères et positions#
un repère fixe \(R_0\)
3 repères mobiles \(R_1,R_2,R_3\)
centre de gravite : \(\vec{OG} = h \vec{Z_2}\)
point \(P\) sur la périphérie de la toupie: \(\vec{GP} = R \vec{X_3}\)
# reperes et points
O = Point('O')
R0 = ReferenceFrame('R_0')
#
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[theta, R0.z])
#
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[phi, R1.y])
#
R3 = ReferenceFrame('R_3')
R3.orient(R2,'Axis',[psi, R2.z])
# centre de gravite
G = Point('G')
# point P
P = Point('P')
7.2.3. question 1#
Dans la cellule suivante, définir la position de G et de P en utilisant la methode .set_pos(point, valeur)
On rappelle que les vecteurs unitaires d’un repère R0 sont notés en python:
R0.x R0.y et R0.z
# G.set_pos()
# P.set_pos()
### BEGIN SOLUTION
G.set_pos(O,h*R2.z)
P.set_pos(G,R*R3.x)
### END SOLUTION
display("OG=",G.pos_from(O),"GP=",P.pos_from(G))
assert(G.pos_from(O).dot(R2.z) == h)
assert(P.pos_from(G).dot(R3.x) == R)
'OG='
'GP='
7.2.4. question 2#
Dans la cellule suivante, calculer la position de P dans le reférentiel \((O,R_0)\), et mettre dans les variables xp, yp et zp, les coordonnées de P dans ce référentiel.
On utilisera la méthode .pos_from(point) , .express(repère) et .dot(vecteur)
# calcul de xp et yp
xp = 0
yp = 0
zp = 0
### BEGIN SOLUTION
xp = P.pos_from(O).dot(R0.x)
yp = P.pos_from(O).dot(R0.y)
zp = P.pos_from(O).dot(R0.z)
### END SOLUTION
display("xp=",xp,"yp=",yp,"zp=",zp)
assert ( xp == Vector.dot(Point.pos_from(P,O),R0.x) )
assert ( yp == Vector.dot(Point.pos_from(P,O),R0.y) )
assert ( zp == Vector.dot(Point.pos_from(P,O),R0.z) )
'xp='
'yp='
'zp='
7.3. Etude cinématique#
application de la composition des vitesses
Si on connait la vitesse de P dans le repère \(R_1\) et on connaît la vitesse de M par rapport à un autre repère \(R_0\), alors on utilise la méthode P.v1pt_theory(M,R0,R1)
Si les 2 points M et P sont fixes dans le repère \(R_1\) et on connaît la vitesse de M par rapport à un autre repère \(R_0\), alors on utilise la méthode P.v2pt_theory(M,R0,R1)
objectif: calcul de la vitesse dans différents repères par projection
7.3.1. question 3: vitesse des points / aux repères#
En utilisant la composition de vitesse, calculer dans la cellule suivante la vitesse du point G et du point P par rapport à R0 sachant que :
\(\vec{V}_O/R_0 = 0\)
\(\vec{V}_G/R_2 = 0\)
\(\vec{V}_P/R_3 = 0\)
# definition et calcul des vitesses
O.set_vel(R0,0.)
G.set_vel(R2,0.)
P.set_vel(R3,0.)
# calcul vitesse de G / a R0: composition des vitesses
# et vitesse de P / a R0
### BEGIN SOLUTION
G.v1pt_theory(O,R0,R2)
P.v2pt_theory(G,R0,R3)
### END SOLUTION
display("VG=",G.vel(R0),"VP=",P.vel(R0))
assert ( G.vel(R0) == Point.v1pt_theory(G,O,R0,R2) )
assert ( P.vel(R0) == Point.v2pt_theory(P,G,R0,R3) )
'VG='
'VP='
7.3.2. question 4: calcul de VG dans R0#
en utilisant une des méthodes .pos_from(point), .express(frame), .dot(vecteur), .diff(t), et .simplify(), calculer les quantités suivantes dans la cellule suivante:
calculer les composante de OG suivant R0.x, R0.y, R0.z dans les variables Gx0,Gy0 et Gz0
en déduire les composante de la vitesse de G suivant R0.x, R0.y, R0.z, dans les variable VGx0,VGy0,VGz0
# composante de OG et VG suivant R0.x
Gx0 = 0
Gy0 = 0
Gz0 = 0
VGx0 = 0
VGy0 = 0
VGz0 = 0
### BEGIN SOLUTION
Gx0 = G.pos_from(O).dot(R0.x)
Gy0 = G.pos_from(O).dot(R0.y)
Gz0 = G.pos_from(O).dot(R0.z)
VGx0 = Gx0.diff(t)
VGy0 = Gy0.diff(t)
VGz0 = Gz0.diff(t)
### END SOLUTION
display("OG=",Gx0*R0.x+Gy0*R0.y+Gz0*R0.z,"VG=",VGx0*R0.x+VGy0*R0.y+VGz0*R0.z)
assert((VGx0==sp.diff(Gx0,t)) and (VGy0==sp.diff(Gy0,t)) and (VGz0==sp.diff(Gz0,t)))
assert((VGx0==G.vel(R0).dot(R0.x)) and (VGy0==G.vel(R0).dot(R0.y)) and (VGz0==G.vel(R0).dot(R0.z)))
'OG='
'VG='
7.3.3. question 5: calcul de la vitesse de G et P par rapport à R1#
dans la cellule suivante
Calculer OG dans R1 et mettre le résultat dans la variable OG1
En déduire la vitesse de G par rapport à (O,R1), et mettre le résultat dans la variable VG1 (vitesse relative de P / a R1)
Calculer GP dans R2 et mettre le résultat dans la variable GP2
En déduire la vitesse de P par rapport à (G,R2), et mettre le résultat dans la variable VP2 (vitesse relative de P / a R2)
OG1 = 0
VG1 = 0
OP1 = 0
VP1 = 0
### BEGIN SOLUTION
OG1 = G.pos_from(O).express(R1)
VG1 = OG1.diff(t,R1)
GP2 = P.pos_from(G).express(R2)
VP2 = GP2.diff(t,R2).express(R2).simplify()
### END SOLUTION
display("OG1=",OG1,"VG1=",VG1)
display("OP2=",GP2,"VP2=",VP2)
assert(OG1==Vector.express(Point.pos_from(G,O),R1))
assert(VG1==Vector.diff(OG1,t,R1))
assert(GP2==Vector.express(Point.pos_from(P,G),R2))
assert(VP2==Vector.diff(GP2,t,R2))
'OG1='
'VG1='
'OP2='
'VP2='
7.4. Calcul des trajectoire du point G et du point P#
On étudie tout d’abord le mouvement pour des valeurs \(\phi(t)\) et \(\theta(t)\) connues
7.4.1. paramètres géométriques#
# parametres numériques
from validation.AngleEuler import Trajectoire
valnum = [(R,_R), (h,_h), (g,10) ]
display(valnum)
7.4.2. cas particuliers 1 \(\phi=cste\)#
Dans le cas d’une précession telle que \(\dot{\theta} = \omega = cste\) avec un angle de nutation \(\phi=\phi_0=cste\) et une rotation propre t.q. \(\dot{\psi}=\Omega=cste\)
7.4.2.1. question 6#
En utilisant les paramètres suivants, définir les expression sde \(\theta,\phi,\psi\) en fonction de t dans la variable vals (liste) ainsi que le temps tmax d’étude de la trajectoire correspondant à une rotation de la toupie autour de \(R_0.z\).
La valeur de \(\omega\) est dans la variable omega et la valeur de \(\Omega\) est dans la variable Omega
printmd("paramétres de l'étude: omega={}rd/s Omega={}rd/s phi0={}rd".format(_omega,_Omega,_phi0))
paramétres de l’étude: omega=6rd/s Omega=30rd/s phi0=0rd
# definition des lois theta, pho et psi fonction de t
vals = [ (theta,0) , (phi, 0) , (psi, 0)]
tmax = 0
### BEGIN SOLUTION
vals = [ (theta, _omega*t), (phi, _phi0), (psi, _Omega*t)]
tmax = np.round(2*np.pi/_omega,3)
### END SOLUTION
print("tmax=",tmax)
display("vals=",vals)
assert (t in vals[0][1].free_symbols) and ((t in vals[2][1].free_symbols))
tmax= 1.047
'vals='
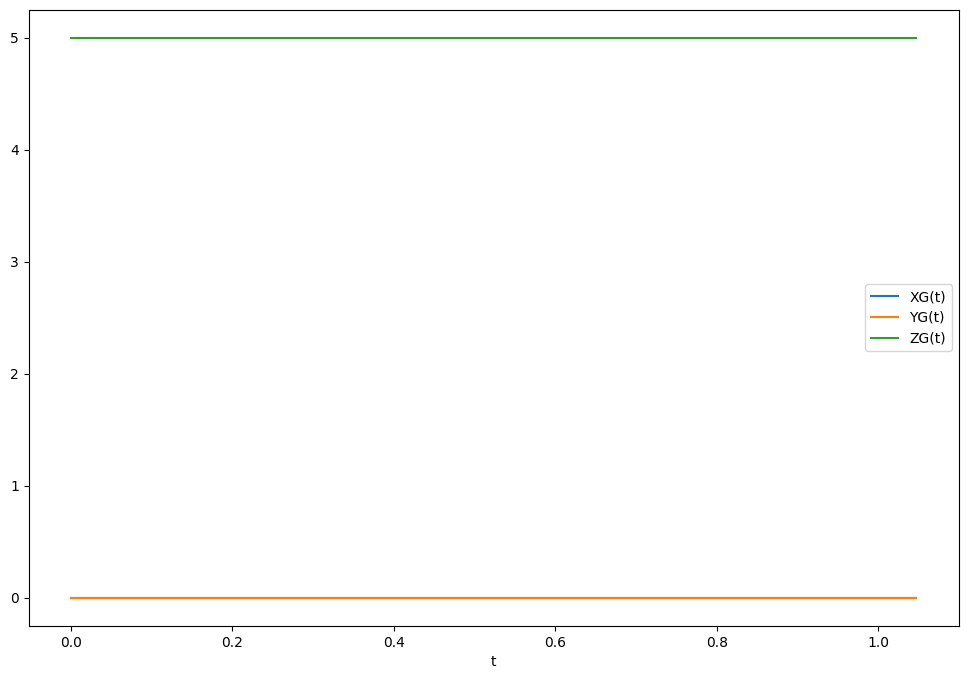
7.4.2.2. Trajectoire de G#
On en déduit la position de G en fonction de t dans OG permettant de tracer la trajectoire en substituant les valeurs numériques
# calcul trajectoire
OG=G.pos_from(O).express(R0).subs(vals).subs(valnum)
display(OG)
traj = Trajectoire(OG,R0,t,tmax)
# courbes
traj.plot()
# trajectoire en 3D
traj.trace()
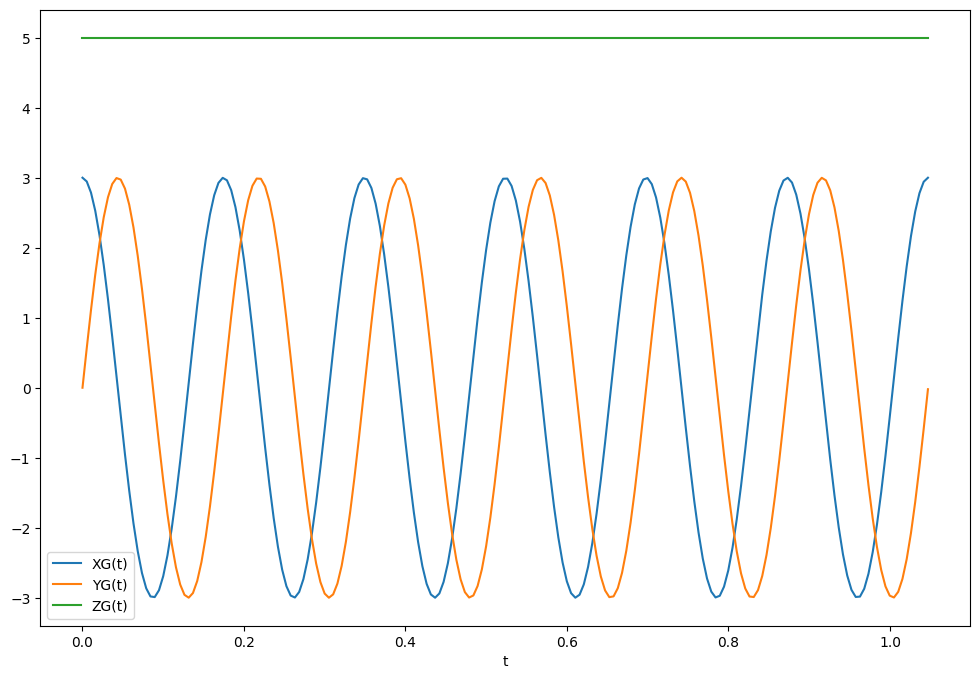
7.4.2.3. Trajectoire de P#
On en déduit la position de P en fonction de t dans OP permettant de tracer la trajectoire en substituant les valeurs numériques
# calcul trajectoire
OP=P.pos_from(O).express(R0).subs(vals).subs(valnum)
display(OP)
traj = Trajectoire(OP,R0,t,tmax)
# courbes
traj.plot()
# trajectoire en 3D
traj.trace()
7.4.3. cas particulier 2: \(\dot{\theta} =cste\) et \(\dot{\psi} =cste\)#
on définit les lois \(\theta(t)\) \(\phi(t)\) et \(\psi(t)\) telles que \(\dot{\theta} = \omega = cste\) , \(\dot{\phi}==cste\) et \(\dot{\psi}=\Omega=cste\)
7.4.3.1. question 7#
En utilisant les paramètres suivants, définir les expression sde \(\theta,\phi,\psi\) en fonction de t dans la variable vals (liste) ainsi que le temps tmax d’étude de la trajectoire correspondant à une rotation de la toupie autour de \(R_0.z\).
printmd("paramétres de l'étude: omega={}rd/s Omega={}rd/s phip={}rd/s".format(_omega,_Omega,_phip))
paramétres de l’étude: omega=6rd/s Omega=30rd/s phip=3rd/s
# definition des lois theta, pho et psi fonction de t
vals = [ (theta,0) , (phi, 0) , (psi, 0)]
tmax = 0
### BEGIN SOLUTION
vals = [ (theta, _omega*t), (phi, _phip*t), (psi, _Omega*t)]
tmax = np.round(4*np.pi/_omega,3)
### END SOLUTION
print("tmax=",tmax)
display("vals=",vals)
assert (t in vals[0][1].free_symbols) and ((t in vals[2][1].free_symbols))
tmax= 2.094
'vals='
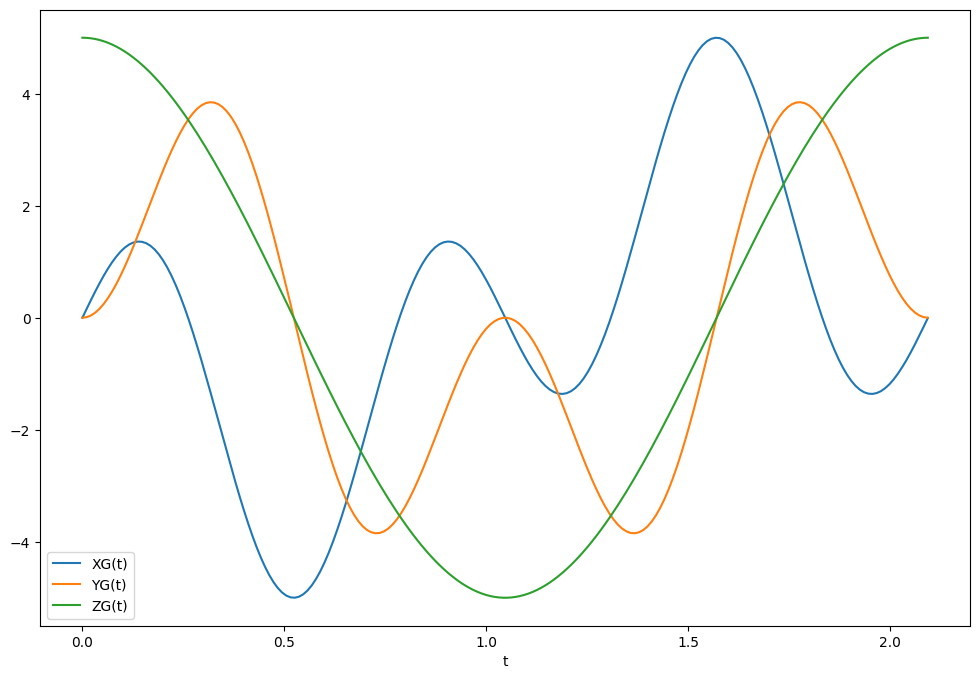
7.4.3.2. Trajectoire de G#
On en déduit la position de G en fonction de t dans OG permettant de tracer la trajectoire en substituant les valeurs numériques
# calcul trajectoire
OG=G.pos_from(O).express(R0).subs(vals).subs(valnum)
display(OG)
traj = Trajectoire(OG,R0,t,tmax)
# courbes
traj.plot()
# trajectoire 3D
traj.trace()
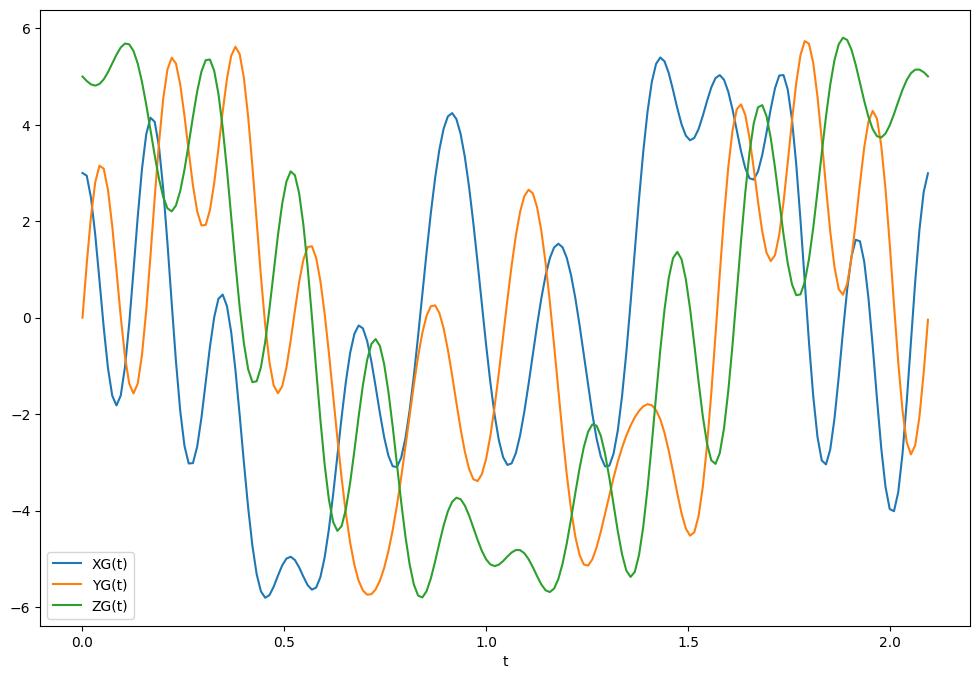
4.4 Trajectoire de P
On en déduit la position de P en fonction de t dans OP permettant de tracer la trajectoire en substituant les valeurs numériques
# calcul trajectoire
OP=P.pos_from(O).express(R0).subs(vals).subs(valnum)
display(OP)
traj = Trajectoire(OP,R0,t,tmax)
# courbes
traj.plot()
# trajectoire 3D
traj.trace()
7.4.3.3. question 8#
calculer la norme de la vitesse de G et de P et mettre l’expression dans les 2 variables VG et VP.
On pourra utiliser la méthode .vel(R0) puis .magnitude() pour calculer l’amplitude de la vitesse, puis la méthode .subs(vals).subs(valnum).doit() pour substituer dans l’expression les valeurs numériques fonctions de t de \(\theta\), \(\phi\) et \(\psi\) ainsi que la valeur de R et h.
VP = 0
VG = 0
### BEGIN SOLUTION
VG = G.vel(R0).magnitude().simplify().subs(vals).subs(valnum).doit()
VP = P.vel(R0).magnitude().simplify().subs(vals).subs(valnum).doit()
### END SOLUTION
display("VG=",VG,"VP=",VP)
assert ((t in VG.free_symbols) and (t in VP.free_symbols))
'VG='
'VP='
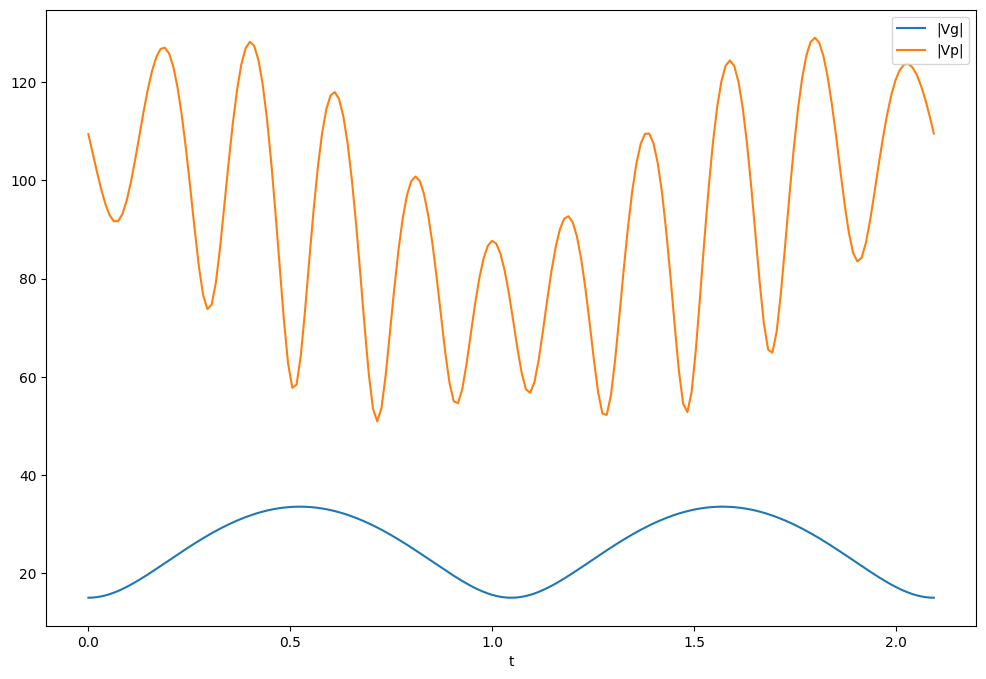
traj.plotvit(VG,VP)
7.4.4. Bilan de l’étude cinématique#
Faite l’analyse de la trajectoire de G et de P , de leurs vitesses ainsi que vos conclusions en utilisant le plan suivant. On déterminera en particulier sur quelle surface particulière se trouve chacune des trajectoires de G et P
7.4.4.1. Analyse de la trajectoire de G et de sa vitesse#
7.4.4.2. Analyse de la trajectoire de P et de sa vitesse#
7.4.4.3. Conclusion#
7.5. Etude Dynamique#
On va maintenant calculer l’évolution des 3 angles \(\phi\),\(\theta\) et \(\psi\) en appliquant le Principe Fondamental de la Dynamique (PFD)
Pour cela on fait tout d’abord le bilan des efforts exercées sur la toupie. On suppose que la toupie tourne sans frottement autour de O, donc les efforts extérieurs se réduisent:
au poids \(\vec{P} = -m g \vec{z_0}\)
à la réaction \(\vec{T}\) au point \(O\) dont la direction est à priori quelconque mais s’il n’y a pas de frottement, cette réaction n’a pas de couple \(C_f\) en \(O\)
7.5.1. équations du mouvement: PFD#
le bilan de variation de la quantité de mouvement s’écrit: $\( \frac{d}{dt} m \vec{V_G} = \vec{P} + \vec{T}\)\( \)\phi\(,\)\theta\( et \)\psi$
le bilan de variation du moment cinétique s’ecrit en O (point fixe) $\(\frac{d}{dt}\overrightarrow{\sigma}(O)= \vec{OG}\wedge\vec{P}\)\( qui donnent les 3 équations différentielles du mouvement permettant de calculer l'évolution des 3 angles \)\phi\(,\)\theta\( et \)\psi$
A ces équations s’ajoutent des propriétes de conservation
la conservation de l’énergie totale \( E = E_c + E_p\)
la conservation du moment cinétique suivant \(\vec{z_0}\) et suivant \(\vec{z_2}\)
7.5.2. Bilan sur la modélisation dynamique#
Ecrire Votre réponse ici
7.5.2.1. justification du choix du calcul du moment cinétique en O au lieu de G#
7.5.2.2. justification de l’utilisation du bilan du moment cinétique#
cette équation vectorielle permet de calculer la réaction inconnue \(\vec{T}\) connaissant les 3 angles
7.5.2.3. justification des propriétés de conservation#
7.6. Equations du mouvement#
7.6.1. définition des paramètres#
définition du solide
masse
moment d’inertie
solide avec
RigidBody
# parametres
m = sp.symbols('m')
# moment d'inertie d'un disque rayon R
I1 = m*R**2/2
I2 = m*R**2/4
IG = inertia(R2,I2,I2,I1)
# Définition du solide toupie avec R3 repere lié à la toupie
toupie = RigidBody('Toupie',G,R3,m,(IG,G))
7.6.2. Calcul du moment cinétique#
en utilisant la fonction angular_momentum on calcule le moment cinétique en O de la toupie, puis on calcule l’énergie potentielle pour en déduire l’énergie totale
# calcul moment cinétique en O
sigmaO = angular_momentum(O,R0,toupie).simplify()
display("sigma_O=",sigmaO)
toupie.potential_energy = m*g*dot(G.pos_from(O),R0.z)
Et = (toupie.kinetic_energy(R0) + toupie.potential_energy).simplify()
display("Et=",Et)
'sigma_O='
'Et='
7.6.3. Equations du mouvement#
en dérivant le moment cinétique sigmaO avec la fonction time_derivative(sigmaO,R0) et en calculant le moment du poids en O en utilisant ^ pour le produit vectoriel, écrire l’équation de bilan du moment cinétique en O dans la variable Eqs
dsigmaO = 0
Mp = 0
Eqs = 0
### BEGIN SOLUTION
# dérivee mt cinetique
dsigmaO = time_derivative(sigmaO,R0)
# mt des forces
Mp = G.pos_from(O) ^ (-m*g*R0.z)
# equation
Eqs = dsigmaO - Mp
### END SOLUTION
display("Equations du mvt:",Eqs)
assert(Eqs.free_symbols(R0)=={R,g,m,h,t})
'Equations du mvt:'
print("projection des equations dans R2")
# équations projetés dans R2
display(sp.Eq(Eqs.dot(R2.x),0))
display(sp.Eq(Eqs.dot(R2.y),0))
display(sp.Eq(Eqs.dot(R2.z),0))
projection des equations dans R2
7.6.4. simplification des équations#
simplifier le système d’équations précédentes divisant par \(mR^2\) et mettre le résultat dans les variables
eq1, eq2 , eq3
# simplication par / m*R**2
eq1 = 0
eq2 = 0
eq3 = 0
### BEGIN SOLUTION
eq1 = (Eqs.dot(R2.x)*4/(m*R**2)).simplify()
eq2 = (Eqs.dot(R2.y)*2/(m*R**2)).simplify().expand()
eq3 = (Eqs.dot(R2.z)*2/(m*R**2)).simplify()
### END SOLUTION
display("eq1=0",eq1)
display("eq2=0",eq2)
display("eq3=0",eq3)
assert(eq1.free_symbols == {R,h,t})
assert(eq2.free_symbols == {R,h,t,g})
assert(eq3.free_symbols == {t})
'eq1=0'
'eq2=0'
'eq3=0'
7.6.5. Integrales premières / mR^2#
calculer dans Ec et Et l’expression simplifié par \(mR^2\) de l’énergie cinétique et potentielle
Ec = 0
Ep = 0
### BEGIN SOLUTION
Ec = (toupie.kinetic_energy(R0)*8/(m*R**2)).simplify()
Ep = (toupie.potential_energy*8/(m*R**2)).simplify()
### END SOLUTION
display("Et=",Ec+Ep)
display("sigmaO.z0=",(dot(sigmaO,R0.z)*4/(m*R**2)).simplify().expand())
display("sigmaO.z2=",(dot(sigmaO,R2.z)/(m*R**2)).simplify())
assert(Ec.free_symbols == {R,h,t})
assert(Ep.free_symbols == {R,h,g,t})
'Et='
'sigmaO.z0='
'sigmaO.z2='
7.6.6. simulation numérique#
choisir des valeurs pour les conditions initiales pour le vecteur \(Y(t)\)
$\( Y(t) = [\theta, \dot{\theta}, \phi, \dot{\phi}, \psi, \dot{\psi}] \)$
et mettre le résultat dans la variable Y0.
Choisir aussi la valeur du temps tmax d’intégration des équations.
On pourra tester différentes conditions initiales en particulier pour obtenir
un mouvement de précession uniquement
un mouvement avec de petits festons
un mouvement avec des festons importants
display("parametres:",valnum)
# choix de la CI
Y0 = 0
tmax = 0
### BEGIN SOLUTION
Y0 = np.array([0.,np.pi/4,0.,-8.,8.,100.])
Y0 = np.array([0.,_omega,0,_phip,0,_Omega])
tmax = 10.0
# festons
Y0 = np.array([0.,np.pi/4,0.,1.,0.,30.])
tmax = 30.0
### END SOLUTION
print("CI=",Y0,"tmax=",tmax)
'parametres:'
CI= [ 0. 0.78539816 0. 1. 0. 30. ] tmax= 30.0
On utilise une bibliothèque Toupie pour intégrer les équations et calculer la solution numérique, puis ensuite visualiser la trajectoire en 2D et 3D.
from validation.Toupie import Toupie
# parametres du problème: 6 ddl (V), 3 equations (EQS), coordonnées du centre de gavité (CG) et energie (EN)
V = [theta,phi,psi,theta.diff(t),phi.diff(t),psi.diff(t)]
EQS = [eq1.subs(valnum),eq2.subs(valnum),eq3.subs(valnum)]
CG = [G.pos_from(O).dot(R0.x).subs(valnum),
G.pos_from(O).dot(R0.y).subs(valnum),
G.pos_from(O).dot(R0.z).subs(valnum)]
EN = [Ec.subs(valnum),Ep.subs(valnum)]
lmax = float((1.2*h).subs(valnum))
T = Toupie(V,EQS,CG,EN,lmax)
# calcul de la solution numérique
T.solve(Y0,tmax)
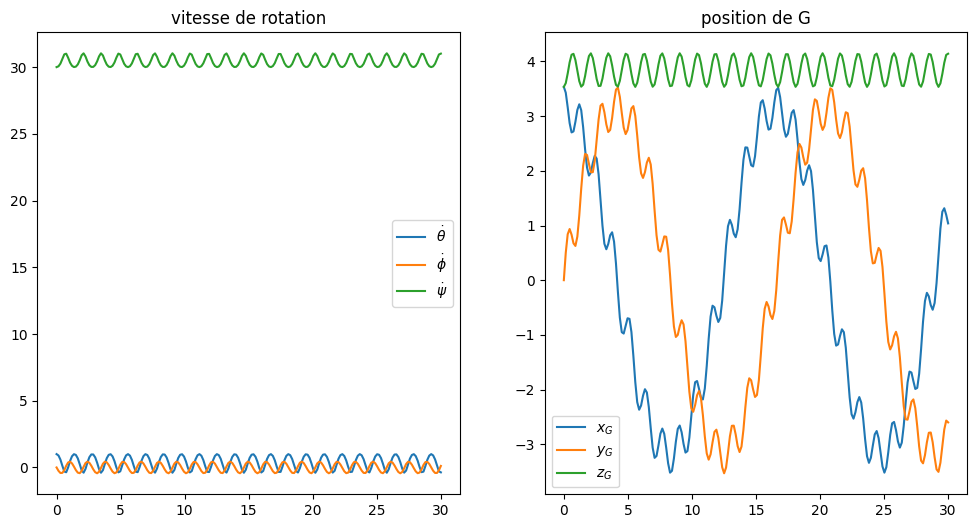
# tracer de la solution angles et positions de G
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(T.t,T.THETAP,label="$\dot{\\theta}$")
plt.plot(T.t,T.PHIP,label="$\dot{\phi}$")
plt.plot(T.t,T.PSIP,label="$\dot{\psi}$")
plt.title('vitesse de rotation')
plt.legend()
plt.subplot(1,2,2)
plt.plot(T.t,T.XG,label="$x_G$")
plt.plot(T.t,T.YG,label="$y_G$")
plt.plot(T.t,T.ZG,label="$z_G$")
plt.title('position de G')
plt.legend();
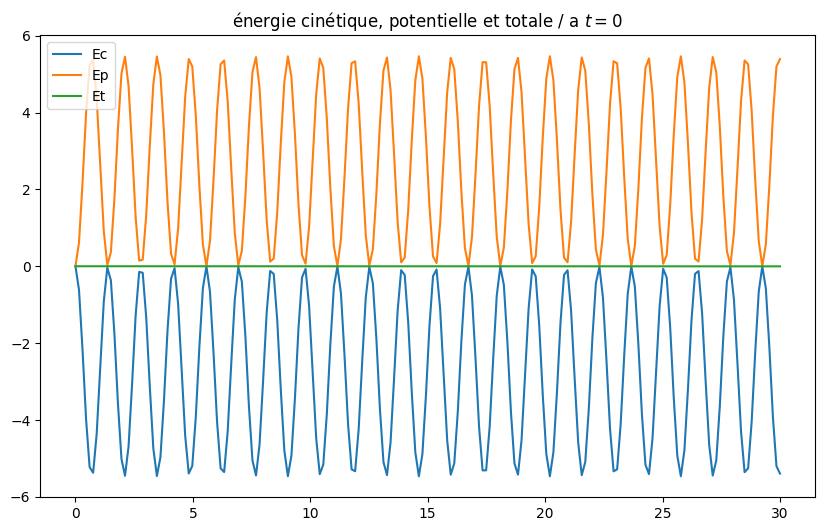
# tracer de l'énergie du système
plt.figure(figsize=(10,6))
plt.plot(T.t,T.EC-T.EC[0],label="Ec")
plt.plot(T.t,T.EP-T.EP[0],label="Ep")
plt.plot(T.t,T.EC+T.EP-T.EC[0]-T.EP[0],label="Et")
plt.title("énergie cinétique, potentielle et totale / a $t=0$")
plt.legend();
print("Mouvement toupie")
T.trace()
T.trajectoire()
Mouvement toupie
