TP mouvement linéarisé du pendule double

4. TP mouvement linéarisé du pendule double#

Marc BUFFAT, dpt mécanique, Université Lyon 1

Attention il faut exécuter la cellule vide suivante !!

%matplotlib inline
import numpy as np
import sympy as sp
from matplotlib import pyplot as plt
from validation.valide_markdown import test_markdown, test_code
from validation.validation import info_etudiant, bib_validation
from IPython.display import display, Markdown, clear_output
bib_validation('cours','MGC2028L')
from Pendule_double import Pendule_double
from Pendule_doubleNL import Pendule_doubleNL
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_  = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("## Etudiant {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
#
_mcl0_ = [ 'degrés', 'liberté', 'paramétres', 'angles', 'longueurs', 'masses',' pendule', 'double','Runge','Kutta' ] 
_mcl1_ = ['phase','opposition','fréquence','modes', 'propres']
# parametres
_alpha = sp.S(np.random.randint(1,5))/sp.S(np.random.randint(1,5))
_beta  = sp.S(np.random.randint(1,5))/sp.S(np.random.randint(1,5))
_omega1 = sp.S(np.random.randint(2,6))
#
display("Parametres (alpha,beta,omega1)=",[_alpha,_beta,_omega1])

_alpha = sp.S(4)/3
_beta = sp.S(1)/2
_omega1 = 4
display(_alpha,_beta,_omega1)

try:
    printmd("INITIALISATION OK!")
except:
    print("Erreur vous n'avez pas executée la cellule vide précédente !")
    print("Votre Notebook n'est pas initialisé correctement !")

4.1. Démarche#

En utilisant le travail de préparation (lien ici), définir la démarche à utiliser et les différentes étapes pour réaliser cette modélisation du mouvement du double pendule, avec en particulier:

  • le problème à étudier: ces paramètres et les degrés de liberté

  • la mise en équations et le nombre de degrés de liberté

  • les calculs à faire et la méthode numérique utilisée

  • les fonctions python à écrire

  • la validation

  • l’analyse à faire

Ecrire le texte récapitulatif de la démarche sur une dizaine de lignes dans la cellule suivante

assert(test_markdown('TP_pendule_double.ipynb','cell-comment0',minm=40,maxe=0.3,mcl=_mcl0_,maxs=0.7))

# importation des bibliotheques
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
import sympy as sp
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
from IPython.display import HTML

4.2. Modélisation mécanique#

On utilise la bibliothèque mechanics de sympy pour mettre en équation le système mécanique constitué de 2 masses \(m_1\) et \(m_2\) accrochées ensemble avec des tiges rigides de longueur \(l_1\) et \(l_2\) de masse négligeables. On suppose que le frottement sur les axes de rotation en O et P1 sont négligeables.

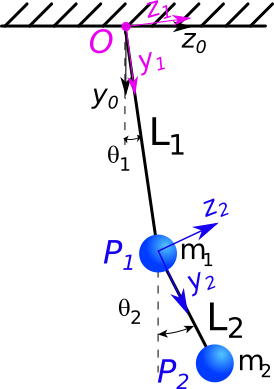
On doit donc définir:

  1. les parametres du problème: longueur et masse des 2 pendules \(l_1,m_1,l_2,m_2\)

  2. les 2 ddl du problème: \(\theta_1(t)\) et \(\theta_2(t)\)

  3. les repères:

  • \(R_0\) repère fixe

  • \(R_1\) repère lié au pendule 1

  • \(R_2\) repère lié au pendule 2

  1. les points: O fixe, \(P_1\) et \(P_2\)

REMARQUE pour obtenir les équations du mouvement que l’on va résoudre numériquement, on va utiliser un outil de calcul symbolique. Si vous n’arrivez pas à obtenir ces équations, vous pouvez faire le calcul avec un papier et crayon. En effet, comme indiqué dans le notebook de préparation, on vous donne la forme des équations, et il reste juste à calculer la valeur numérique des coefficients et rentrer directement ces équations dans la section Equations du mouvement pour continuer le notebook.

from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, Particle
from sympy.physics.vector import vector
# définition des parametres du problème
l1, m1, l2, m2, g, t = sp.symbols('l_1 m_1 l_2 m_2 g t')
# degrés de liberté
theta1, theta2 = dynamicsymbols('theta_1 theta_2')

# définition des reperes et points
O = Point('O')
R0 = ReferenceFrame('R_0')
# pendule 1
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[theta1, R0.x])
P1 = Point('P_1')
P1.set_pos(O,l1*R1.y )
# pendule 2
R2 = ReferenceFrame('R_2')
R2.orient(R0,'Axis',[theta2, R0.x])
P2 = Point('P_2')
P2.set_pos(P1,l2*R2.y )

4.2.1. Calcul des vitesses#

en écrivant que O est fixe dans R0, que P1 est fixe dans R1 et P2 est fixe dans R2, calculer la vitesse de P1 et P2 dans le repère R0 en utilisant la composition des vitesses:

  • méthode v1pt_theory()

on utilisera aussi la méthode .simplify() pour simplifier les expressions

O.set_vel(R0,0)
P1.set_vel(R1,0)
P2.set_vel(R2,0)
### BEGIN SOLUTION
### END SOLUTION

display("VP1 = ",P1.vel(R0))
display("VP2 = ",P2.vel(R0))
assert(P1.vel(R0).dot(R1.y)==0)
assert(P2.vel(R0) != 0)

4.2.2. Calcul des quantités de mouvement#

On définit les 2 points matériels du pendule double Pa1 et Pa2.

Dans la cellule suivante, calculer la dérivée dans R0 de la quantité de mouvement des 2 points et mettre le résultat dans les variables ma1 et ma2 .

On utilisera les méthodes .linear_momentum(R0) et .diff(t,R0) et on simplifiera avec .simplify()

Pa1 = Particle('Pa_1',P1,m1)
Pa2 = Particle('Pa_2',P2,m2)

ma1 = 0
ma2 = 0
### BEGIN SOLUTION
### END SOLUTION

display("ma1 = ",ma1)
display("ma2 = ",ma2)
assert(type(ma1) == vector.Vector)
assert(type(ma2) == vector.Vector)

4.2.3. Bilan des forces#

les forces appliquées sont:

  • la force de gravité suivant \(\vec{y_0}\)

  • les tensions exercées sur les masses par les cables s’écrivent

    \[ T_1\vec{y_1} \mbox{ , } T_2\vec{y_2}\]

en notant \(T_1\) et \(T_2\) l’intensité des tensions, que l’on définit comme inconnues (symboles) du problème.

Calculer la somme des forces exercées sur la masse \(m_1\) et sur la masse \(m_2\) dans les variables F1 et F2

T1, T2 = sp.symbols('T_1 T_2')
F1 = 0
F2 = 0
### BEGIN SOLUTION
### END SOLUTION

display("F1 = ",F1)
display("F2 = ",F2)
assert(type(F1) == vector.Vector)
assert(type(F2) == vector.Vector)
assert(T1 in F1.free_symbols(R0) and T2 in F1.free_symbols(R0))
assert(not (T1 in F2.free_symbols(R0)) and T2 in F2.free_symbols(R0))

4.3. Mise en équation: application du PFD#

On va appliquez le principe fondamental de la dynamique pour obtenir les équations du mouvement:

  1. pour obtenir la première équation du mouvement, appliquer le PFD au système constitué par les 2 masses \(m_1\) et \(m_2\) en projetant suivant \(\vec{z_1}\)

  2. pour obtenir la seconde équation du mouvement, appliquer le PFD au système constitué par la masses \(m_2\) en projetant suivant \(\vec{z_2}\)

En divisant la première équation par \(m_2 l_1\) et la seconde par \(m_2 l_2\), ecrire les 2 équations obtenues dans les variables eq1 et eq2 après simplification et développement en utilisant les méthodes:

  • .simplify() et .expand()

eq1 = 0
eq2 = 0
### BEGIN SOLUTION
### END SOLUTION

display("eq1=",eq1)
display("eq2=",eq2)
assert(not( T1 in eq1.free_symbols) and not( T2 in eq1.free_symbols) )
assert(not( T1 in eq2.free_symbols) and not( T2 in eq2.free_symbols) )

4.3.1. Simplification#

On constate que les équations précédentes sont uniquement fonction des paramêtres suivants:

  • \(\alpha = \frac{l_1}{l_2}\) le rapport des longueurs

  • \(\beta = \frac{m_1}{m_2}\) le rapport des masses

  • \(\omega_1 = \sqrt{\frac{g}{l_1}}\) la pulsation propre du 1er pendule

en utilisant une liste des susbstitutions pour remplacer \(g\), \(m_1\) et \(l_1\) en fonction de ces paramêtres, obtenir les nouvelles equations du mouvement fonction uniquement de \(\alpha\), \(\beta\) et \(\omega_1\) dans les variables eq11 et eq22

# alpha rapport des longueurs et beta des masses
alpha, beta, omega1 = sp.symbols('alpha beta omega_1')
eq11 = eq1.subs([(g, omega1**2*l1),(m1,beta*m2),(l1,alpha*l2)])
eq11 = (eq11*alpha).simplify()
eq22 = eq2.subs([(g,alpha*omega1**2*l2),(l1,alpha*l2)])
display("eq11=",eq11)
display("eq22=",eq22)

display("eq11=",eq11)
display("eq22=",eq22)
assert(eq11.free_symbols == {alpha, beta,omega1, t})
assert(eq22.free_symbols == {alpha, t, omega1})

4.3.2. Equations du mouvement#

pour pouvoir analyser et résoudre le système, on va maintenant remplacer tous les paramètres par les valeurs imposées.

Il faut obtenir un système d’équations dependants uniquement de \(\theta_1(t)\) et \(\theta_2(t)\)

Attention ces valeurs sont des valeurs rationnelles (exactes) et non des valeurs numériques réeelles. On les définira en utilisant la fonction sp.S(val) pour définit val en tant que symbole

par exemple le nombre rationnel \(2/3\) est définit comme

   sp.S(2)/sp.S(3)

ou

   2/sp.S(3)

mais pas

   2/3

pour vérifier vous pouvez afficher le type d’une expression avec type(exp)

Définir la liste de substitution vals pour remplacer les paramêtres par les valeurs rationnelles (exactes) imposées, et faire la subsitution pour obtenir les 2 equations à résoudre dans les variables Eq1 et Eq2

On pourra éventuellement recopier les équations du mouvement données dans le travail de préparation dans les variables Eq1 et Eq2 en utilisant la syntaxe sympy: i.e \(\dot{\theta_1}\) s’écrit theta1.diff(t) et \(\ddot{\theta_1}\) theta1.diff(t,t) et en remplaçant les paramètres par leurs valeurs données ci-dessous:

(4.2)#\[\begin{align} \alpha \left( \beta \omega_{1}^{2} \sin{(\theta_{1})} + \beta \frac{d^{2}\theta_{1}}{d t^{2}} + \omega_{1}^{2} \sin{(\theta_{1})} + \frac{d^{2}\theta_{1}}{d t^{2}} \right) + \sin{(\theta_{1} - \theta_{2})} \left(\frac{d\theta_{2}}{d t}\right)^{2} + \cos{(\theta_{1} - \theta_{2})} \frac{d^{2}}{d t^{2}} \theta_{2} = 0\\ \alpha \omega_{1}^{2} \sin{\theta_{2}} - \alpha \sin{(\theta_{1} - \theta_{2})} \left(\frac{d \theta_{1}}{d t}\right)^{2} + \alpha \cos{(\theta_{1}- \theta_{2})} \frac{d^{2} \theta_{1}}{d t^{2}} + \frac{d^{2} \theta_{2}}{d t^{2}} = 0 \end{align}\]
display("Parametres: alpha={},  beta={},  omega1={}".format(_alpha,_beta,_omega1))

vals = [(alpha,sp.S(1)/sp.S(2)),(beta,sp.S(1)/sp.S(4)),(omega1,sp.S(3))]
Eq1 = 0
Eq2 = 0
### BEGIN SOLUTION#vals = [(alpha,_alpha),(beta,_beta),(omega1,_omega1)]
### END SOLUTION

display(sp.Eq(Eq1,0))
display(sp.Eq(Eq2,0))
assert(Eq1.free_symbols == set([t]))
assert(Eq2.free_symbols == set([t]))

4.3.3. Linéarisation des équations#

On se place dans le cadre des petites oscillations:

  • on suppose que \(\theta_1\) et \(\theta_2\) sont petits et que l’on peut approximer au premier ordre \(\sin\theta \approx \theta \) et \(\cos\theta \approx 1\)

  • on néglige les termes quadratiques dans les équations (termes en \(\dot{\theta_1}^2\) et \(\dot{\theta_2}^2\) )

En effectuant ces substitutions dans les équations précédentes, obtenir les 2 équations linéarisées dans les variables eql1 et eql2.

On pourra écrire les équations dans eql1 et eql2

  1. soit en faissant les substitutions avec la fonction subs ,

  2. soit faire la linéarisation sur le papier et réécrire les équations explicitement dans eql1 et eql2, en notant que \(\dot{\theta_1}\) s’écrit theta1.diff(t) et \(\ddot{\theta_1}\) s’écrit theta1.diff(t,t)

Les équations linéarisées s’écrivent sous la forme:

(4.3)#\[\begin{align} \alpha(\beta+1) \omega_{1}^{2} \theta_{1} + \alpha(\beta+1)\frac{d^{2}\theta_{1}}{d t^{2}} + \frac{d^{2}}{d t^{2}} \theta_{2} = 0\\ \alpha \omega_{1}^{2} \theta_{2} + \alpha \frac{d^{2} \theta_{1}}{d t^{2}} + \frac{d^{2} \theta_{2}}{d t^{2}} = 0 \end{align}\]

où il faut remplacer les paramètres par leurs valeurs.

display("Parametres: alpha={},  beta={},  omega1={}".format(_alpha,_beta,_omega1))

# liste de substitution pour les sinus et cosinus
approx = [(sp.sin(theta1),theta1), (sp.sin(theta2),theta2),
          (sp.sin(theta1-theta2),theta1-theta2), (sp.cos(theta1-theta2),1)]
# linearisation
eql1 = 0
eql2 = 0
### BEGIN SOLUTION
# linearisation eq1
# linearisation eq2
### END SOLUTION

display(sp.Eq(eql1,0))
display(sp.Eq(eql2,0))
assert(eql1.free_symbols == set([t]))
assert(eql2.free_symbols == set([t]))

4.3.4. Solution analytique dans un cas simple#

en utilisant la fonction dsolve nous pouvons obtenir une solution analytique correspondant au laché du pendule avec un angle \(\theta_1 = \theta_0\) et \(\theta_2 = 0\) sans vitesse initiale.

On obtiens les 2 solutions dans les variables theta1l et theta2l

theta0 = sp.symbols('theta_0')
C1,C3 = sp.symbols("C1 C3")
eqs = (sp.Eq(eql1,0),sp.Eq(eql2,0))
sol = sp.dsolve(eqs,ics={theta1.subs(t,0):theta0,theta2.subs(t,0):0})
# CI sur dtheta
theta1l=sol[0].rhs.subs([(C1,0),(C3,0)])
theta2l=sol[1].rhs.subs([(C1,0),(C3,0)])
display(sp.Eq(theta1l,0))
display(sp.Eq(theta2l,0))

4.3.5. Tracé de la solution#

en choisissant une valeur de \(\theta_0=\pi/10\), on va tracer l’évolution de la solution au cours du temps en convertissant les solutions analytiques en fonction python de t en utilisant

  • sp.lambdify([t],expression)

On tracera la solution sur 10 periodes du pendule simple (basée sur la valeur de \(\omega_1\) la pulsation du 1er pendule) en prenant 500 points par période.

Définir la valeur numerique de \(\omega_1\) dans la variable Omega1, le tableau tt des temps où on calcule la solution, et la valeurs de la solution en ces temps dans les tableaux Theta1l et Theta2l

# parametres
Theta0 = np.pi/10
Omega1 = 0
dt = 0
tt = 0
Theta1l = 0
Theta2l = 0
### BEGIN SOLUTION
### END SOLUTION

print("Omega1=",Omega1)
assert(tt.size == 5000)
assert(np.abs(Theta1l(0)-Theta0) < 1.e-8)
assert(np.abs(Theta2l(0)) < 1.e-8)

plt.figure(figsize=(10,6))
plt.plot(tt,Theta1l(tt),label="$\\theta_{e1}$")
plt.plot(tt,Theta2l(tt),label="$\\theta_{e2}$")
plt.legend()
plt.xlabel("temps [s]")
plt.ylabel("angle [rd]")
plt.title("Solution analytique en petites oscillations");

4.4. Simulation numérique: mise sous forme matricielle#

pour résoudre numériquement le système d’équations linéarisées,

(4.4)#\[\begin{align} \alpha(\beta+1) \omega_{1}^{2} \theta_{1} + \alpha(\beta+1)\frac{d^{2}\theta_{1}}{d t^{2}} + \frac{d^{2}}{d t^{2}} \theta_{2} = 0\\ \alpha \omega_{1}^{2} \theta_{2} + \alpha \frac{d^{2} \theta_{1}}{d t^{2}} + \frac{d^{2} \theta_{2}}{d t^{2}} = 0 \end{align}\]

nous allons le mettre sous forme matricielle

\[ \mathbf{M} \ddot{Y} + \mathbf{K} Y = 0\]

où \(Y=[\theta_1,\theta_2]\) est le vecteur d’état et \(M\) et \(K\) sont deux matrices (2x2):

  • \(\mathbf{M}\) correspondant aux coefficients numériques de \([\frac{d^{2}}{d t^{2}}\theta_{1}, \frac{d^{2}}{d t^{2}}\theta_{2}]\)

  • \(\mathbf{K}\) correspondant aux coefficients numériques de \([\theta_1, \theta_2]\).

Définir les 2 matrices \(\mathbf{M}\) et \(\mathbf{K}\) dans les deux variables de type Matrix : M et K

Par exemple, pour définir la matrice symbolique A:

(4.5)#\[\begin{bmatrix} a & b \\ c & d \end{bmatrix}\]

on écrit en python sous sympy

   A = Matrix([[a,b],[c,d]])

Définir les 2 matrices M et K de votre problème linéarisé dans les variables M et K.

Attention utilisée des nombres rationnels et pas des nombres réels pour un calcul exacte !

from sympy import Matrix
Y = Matrix([theta1,theta2])
M = 0
K = 0
### BEGIN SOLUTION
### END SOLUTION

display("eql1=",eql1)
display("eql2=",eql2)
display("M=",M)
display("K=",K)
display("equations: ",M*Y.diff(t,t) + K *Y, "=0")
assert(Matrix([eql1,eql2]) == M*Y.diff(t,t) + K *Y)

4.4.1. Simplification#

en multipliant par l’inverse de M, on obtiens un système linéaire simplifié de la forme $\( \ddot{Y} + \mathbf{B} Y = 0 \mbox{ avec } \mathbf{B} = \mathbf{M}^{-1} \mathbf{K} \)$

B = M.inv()*K
display("Matrice B=",B)
Eqs = Y.diff(t,t) + B*Y
display("Equation Eqs=",Eqs)

4.4.2. Simulation numérique du pble linéaire#

Pour résoudre numériquement ce système linéaire avec la méthode de Runge Kutta, nous devons le transformer en un système d’équations différentielles du premier ordre.

On choisit comme vecteur d’etat \(Z = [\theta_1, \theta_2, \dot{\theta_1}, \dot{\theta_2}]\), et on ecrit le système sous la forme $\( \dot{Z} = \mathbf{F} Z\)$

La matrice (4,4) \(\mathbf{F}\) s’écrit en fonction de la matrice \(\mathbf{B}\)

(4.6)#\[\begin{bmatrix} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -B_{1,1} & -B_{1,2} & 0 & 0\\ -B_{2,1} & -B_{2,2} & 0 & 0 \end{bmatrix}\]

Définir la matrice \(\mathbf{F}\) comme une matrice (4,4) numpy dans la variable FB dans la cellule suivante, puis en déduire dans la seconde cellule la fonction second membre double_pendule() qui calcule le second membre du système d’EDO du 1er ordre.

On vérifiera ensuite cette fonction en l’appelant pour un état tq \(\theta_1=0.1\), \(\theta_2=0.2\), \(\dot{\theta_1}=0\) , \(\dot{\theta_2}=0\) à \(t=0\)

FB = 0
### BEGIN SOLUTION
### END SOLUTION

print("Matrice numerique FB=\n",FB)
assert(np.linalg.det(FB) != 0)

def double_pendule(etat,temps=0):
    '''
    calcul le second membre du système du double pendule
    
    Arguments
    ---------   
    etat :  vecteur d'etat [theta1,theta2,dtheta1,dtheta2]
    temps:  instant t du calcul
    
    Retour 
    -------
    derivs:  derivée du vecteur d'etat 
    '''    
    global FB

printmd("### Verification: appel de la fonction")
### BEGIN SOLUTION
### END SOLUTION

assert(test_code('TP_pendule_double.ipynb','cell-verif1','double_pendule('))
assert(np.allclose(double_pendule([0,0,1,1]),[1.,1.,0.,0.]))

def iterationRK2(etat, smb, temps, dt):
    '''Iteration de RungeKutta 2 pour calculer l'évolution de l'etat sur un pas en temps. 
    
    Arguments
    ---------
    etat : vecteur d'etat
    smb  : fonction qui calcule le second membre de l'EDO fonction de l'etat et du temps
    temps: instant du début du calcul
    dt   : pas en temps 
    
    Retour
    -------
    etat_suiv: movelle valeur du vecteur d'etat après une iteration en temps       
    '''
   
    etat_milieu = etat + smb(etat,temps) * dt*0.5
    etat_suiv   = etat + smb(etat_milieu, temps * 0.5) *dt
    return etat_suiv

4.4.3. Choix des parametres#

En prenant les mêmes paramètres que pour la solution analytique, effectuer la simulation numérique et calculer la solution dans la variable num_sol.

On utilisera donc le même tableau tt des temps et le même pas en temps dt.

On compare ensuite la solution numérique avec la solution analytique.

num_sol = 0
### BEGIN SOLUTION
# solution par la méthode RK2
#Set intial conditions
# calcul de la solution 
### END SOLUTION

assert(num_sol.size == 4*tt.size)
assert(np.allclose(num_sol[0],[Theta0,0,0,0]))

# trace de la solution
Theta1 = num_sol[:,0]
Theta2 = num_sol[:,1]
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(tt,Theta1,label="$\\theta_1$")
plt.plot(tt,Theta2,label="$\\theta_2$")
plt.legend()
plt.ylabel("angle [rad]")
plt.title("Solution numérique et erreur")
plt.subplot(2,1,2)
plt.plot(tt,Theta1-Theta1l(tt),label="$\\theta_1 - \\theta_{1e}$")
plt.plot(tt,Theta2-Theta2l(tt),label="$\\theta_2 - \\theta_{2e}$")
plt.legend()
plt.ylabel("erreur [rad]")
plt.xlabel("temps [s]");

4.5. Analyse de la solution dans un plan de phase#

On peut faire une analyse en mode propre de la solution du système d’EDO: $\( \mathbf{M} \ddot{Y} + \mathbf{K} Y = 0 \;\equiv\; \ddot{Y} + \mathbf{B} Y = 0\)$

En notant \(\lambda^2\) une valeur propre associée au vecteur propre \(\mathbf{\Lambda}\) de \(\mathbf{B} = \mathbf{M}^{-1} \mathbf{K}\), on a

\[ \mathbf{B} \mathbf{\Lambda} = \lambda^2 \mathbf{\Lambda} \]

et on en déduit une solution élementaire \(Y=\mathbf{\Theta}\) de l’EDO

\[ \mathbf{\Theta(t)} = \mathbf{\Lambda} \cos{\lambda{t}}\]

En calculant les valeurs propres de la matrice B, on en déduit les 2 solutions élémentaires (ou modes propres) dont on calcule les valeurs dans les variables Lb11,Lb12 pour le premier mode propre et Lb12,Lb21 pour le second mode propre.

VP = B.eigenvects()
display(VP)
lambda1=np.sqrt(float(VP[0][0].evalf()))
Lambda1=sp.matrices.dense.matrix2numpy(Theta0*VP[0][2][0],dtype=np.float64).reshape(2)
lambda2=np.sqrt(float(VP[1][0].evalf()))
Lambda2=sp.matrices.dense.matrix2numpy(Theta0*VP[1][2][0],dtype=np.float64).reshape(2)
Lb11 = np.cos(lambda1*tt)*Lambda1[0]
Lb12 = np.cos(lambda1*tt)*Lambda1[1]
Lb21 = np.cos(lambda2*tt)*Lambda2[0]
Lb22 = np.cos(lambda2*tt)*Lambda2[1]

plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.title("Premier mode propre")
plt.plot(tt,Lb11,label="$\\theta_1$")
plt.plot(tt,Lb12,label="$\\theta_2$")
plt.legend()
plt.ylabel("angles [rd]")
plt.subplot(2,1,2)
plt.title("Second mode propre")
plt.plot(tt,Lb21,label="$\\theta_1$")
plt.plot(tt,Lb22,label="$\\theta_2$")
plt.legend()
plt.ylabel("angles [rd]")
plt.xlabel("temps [s]");

4.5.1. Analyse des modes propres#

commenter et analyser ces modes propres dans la cellule suivante, en répondant en particulier aux questions:

  • comment oscillent les 2 pendules dans chacun des modes

  • discuter la phase d’oscillation des 2 pendules

  • comparer aussi les fréquences et les périodes

assert(test_markdown('TP_pendule_double.ipynb','cell-comment1',minm=20,maxe=0.3,mcl=_mcl1_ ,maxs=0.72))

4.5.2. Trace#

Nous allons tracé sur une meme figure \(\theta_2\) et fonction de \(\theta_1\), qui décrivent une courbe de lissajoux généralisée.

On trace aussi les 2 modes propres.

plt.figure(figsize=(8,8))
plt.plot(Theta1,Theta2)
plt.plot(Lb11,Lb12,label="mode propre 1")
plt.plot(Lb21,Lb22,label="mode propre 2")
plt.plot(Theta1[0],Theta2[0],'*',color='k',markersize=16,label='position init.')
plt.xlabel("$\\theta_1$")
plt.ylabel("$\\theta_2$")
plt.legend()
plt.axis('equal')
plt.title("Plan de phases $\\theta_1,\\theta_2$");

4.5.3. Analyse de la solution#

commenter et analyser le graphique obtenu.

  • Que peut on dire de la solution obtenu par rapport aux modes propres

  • Que se passe-t-il si on change les conditions initiales ?

assert(test_markdown('TP_pendule_double.ipynb','cell-comment2',minm=15,maxe=0.3))

4.6. Visualisation du mouvement: animation#

en utilisant la bibliothèque d’animation de matplotlib, on peut tracer la cinématique du mouvement.

Attention: le calcul de l’animation n’est pas instantané et il faut attendre un peu !

pendule_double = Pendule_double(alpha.subs(vals),omega1.subs(vals))

4.6.1. Animation de la solution#

on visualisera les animations dans la section suivante Animations (cliquez ici)

%%capture
# animation solution numerique
pas = 4
pendule_double.solution(Theta1[::pas],Theta2[::pas],pas*dt)
anim = pendule_double.calculanim(titre="petites oscillations")

4.6.2. Animation mode propre 1#

%%capture
pendule_double.solution(Lb11[::pas],Lb12[::pas],pas*dt)
anim1 = pendule_double.calculanim(titre="mode propre 1")

4.6.3. Animation mode propre 2#

%%capture
pendule_double.solution(Lb21[::pas],Lb22[::pas],pas*dt)
anim2 = pendule_double.calculanim(titre="mode propre 2")

4.7. Conclusion#

Ecrire ici vos conclusions sur l’étude

L’étude a permis d’étudier le système mécanique classique du pendule double.

En utilisant un outil de calcul formel sympy, on a pu obtenir les équations du mouvement dans le cas général.

En se plaçant dans le cadre de petites oscillations, on a pu linéariser le système d’équations, et montrer que la solution générale est une combinaison linéaire de deux modes propres d’oscillations: un mode en phase et un mode en opposition de phase.

Pour obtenir la solution dans le cas générale, on a utilisé la méthode d’intégration d’EDO de Runge Kutta, en transformant le système de 2 équations d’ordre 2 en un système de 4 équations d’ordre 2.

En analysant le système dans l’espace des phases, on met en évidence l’importante des 2 modes propres suivant la condition initiale choisie et sa distance par rapport aux axes des modes propres.

Enfin une visualisation du mouvement du pendule permet de conforter cette analyse, en comparant le mouvement avec celui des modes propres suivant les conditions initiales choisies.

assert(test_markdown('TP_pendule_double.ipynb','cell-comment3',minm=20,maxe=0.3))

4.7.1. Animations#

from matplotlib import rc
rc('animation', html='jshtml')
anim

from matplotlib import rc
rc('animation', html='jshtml')
anim1

from matplotlib import rc
rc('animation', html='jshtml')
anim2

4.8. Etude du cas non linéaire (partie optionnelle)#

dans cette partie, on va résoudre numériquement les équations du mouvement dans le cas général en utilisant une méthode numérique basée sur Runeg Kutta que l’on vous fournit.

Vous aurez alors à faire des expériences numériques suivant la valeur de l’angle initiale \(\theta_0\), analyser les résultats et commenter ces résultats

display("Equations à résoudre =",Eq1,Eq2)

# résolution numérique
pendule = Pendule_doubleNL(t,theta1,theta2,Eq1,Eq2)

def double_pendule(state,time=0):
    global pendule
    derivs = pendule.DerivZ(state)
    return derivs

def rk2_step(state, rhs, time, dt):
    '''Update a state to the next time increment using the RK2 method.
    
    Arguments
    ---------
    state : array of dependent variables
    rhs   : function that computes the RHS of the DE, taking (state, time)
    time  : float, time instant
    dt    : float, time increment
    
    Returns
    -------
    next_state : array, updated after one time increment'''
    
    mid_state  = state + rhs(state,time) * dt*0.5    
    next_state = state + rhs(mid_state,time + 0.5*dt)*dt
 
    return next_state

# parametres numériques: étude sur n périodes
omega = float(_omega1)
period = 2*np.pi/omega
dt = period/500
T  = 10*period
N  = round(T/dt)
tt = np.linspace(0, T, N)

4.8.1. simulation numérique#

  • choisir une valeur de la condition initiale Theta0

  • on calcule ensuite la solution numérique dans le vecteur numsolnl à l’aide de la fonction rk2_step

# choix de la condition initiale (faire des essais avec différentes valeurs)
Theta0 = np.pi/4
num_solnl = np.zeros([N,4])
num_solnl[0,0] = Theta0
for i in range(N-1):
    num_solnl[i+1] = rk2_step(num_solnl[i], double_pendule, tt[i], dt)

# tracer de la solution
plt.rc('font', family='serif', size='14')
Theta1_nl = num_solnl[:,0]
Theta2_nl = num_solnl[:,1]
plt.figure(figsize=(10,8))
plt.plot(tt,Theta1_nl,label="$\\theta_1 NL$")
plt.plot(tt,Theta2_nl,label="$\\theta_2 NL$")
plt.legend()
plt.title("Solution non linéaire")
plt.ylabel("angle [rad]")
plt.xlabel("temps [s]");

plt.figure(figsize=(8,8))
plt.plot(Theta1_nl,Theta2_nl)
plt.plot(Theta1_nl[0],Theta2_nl[0],'*',color='k',markersize=16,label='position init.')
plt.xlabel("$\\theta_1$")
plt.ylabel("$\\theta_2$")
plt.legend()
plt.axis('equal')
plt.title("Plan de phases");

%%capture
# animation solution numerique
pas = 4
pendule_double.solution(Theta1_nl[::pas],Theta2_nl[::pas],pas*dt)
anim_nl = pendule_double.calculanim(titre="oscillations non linéaires")

from matplotlib import rc
rc('animation', html='jshtml')
anim_nl

4.8.2. Analyse#

Faire l’analyse du mouvement en effectuant plusieurs simulations pour différentes valeurs de \(\theta_0\). En particulier:

  • que peut on dire du mouvement quand on augmente \(\theta_0\)

  • quelle est la validité du modèle linéaire précédent ?

  • à partir de quelle moment le mouvement devient -il fortement non linéaire

  • le mouvement peut il devenir chaotique comme sur la photo, et si oui à partir de quelle moment ?

assert(test_markdown('TP_pendule_double.ipynb','cell-comment4',minm=20,maxe=0.3))

4.9. FIN du TP#

# version
from platform import python_version,uname,platform
print("Systeme       :",uname())
print("OS            :",platform())
print("version python:",python_version())
print("version sympy :",sp.__version__)
print("version numpy :",np.__version__)
Contenu