Rêgles de programmation sous Python

2. Rêgles de programmation sous Python#

python

Contenu

  1. Rêgles de base

  2. Variables

  3. Liste et dictionnaire

  4. Tableaux Numpy

  5. Coder de façon simple et lisible

  6. Instructions conditionnelles

  7. Instructions de répétition

  8. Fonction et algorithme

  9. Lecture des données sur fichier

  10. Résumé

2.1. Rêgles de base#

  1. Rigueur

  • La programmation scientifique est une école de rigueur !

  1. Savoir et comprendre ce que l’on doit faire

  • Ecrire un algorithme en français décrivant ce que l’on doit faire

  1. Identifier les donnéees et les résultats

  • Définir les données du problème et les résultats attendus

  1. Vérifier et valider

  • Afficher les valeurs intermédiaires du calcul avec print

  • Vérifier le résultat sur des cas simples

2.2. Variables#

dans un programme, les variables permettent de manipuler les données

  1. création (avec initialisation)

       nom = valeur

    • attention on ne peut utiliser une variable que si elle a été initialisée

  2. Définition des variables

Une variable est définit par un nom (identifiant), et une valeur avec un type

  • nom = suite de caractères et de chiffres sans accents ni ponctuation

    • attention majuscule # minuscule

    • utiliser plutôt des noms en minuscule ayant un sens

    • réserver les majuscules pour les constantes

    • utiliser un _ pour les noms longs

  • valeur définie le type. Les types de base

    • chaîne (string ou str) entre "

    • entier (int)

    • réel en virgule flottante (float)

2.3. Liste et dictionnaire#

liste = structure de données qui contient une série de valeurs, de type éventuellement différent, et dont le nombre peut varier.

attention: on compte à partir de 0 en Python

  1. création (liste de valeurs entre [et ])

    ma_liste = [ val1, val2, val3 ]

  2. accès avec un indice à partir de 0

    ma_liste[i]  élément i-1 de la liste
ma_liste[0]  premier élément
ma_liste[-1] dernier élément
ma_liste[debut:fin:pas] sous-liste

dictionnaire: liste avec un accès par mot clés

     dict = { 'cle1': val1, 'cle2': val2 }
     
     dict['cle']  valeur du dictionnaire pour le mot clé

2.4. Tableaux Numpy#

Pour le calcul scientifique, on utilise les tableaux de la bibliothèque numpy. Il faut importer la bibliothèque pour pouvoir l’utiliser

   import numpy as np

A la différence d’une liste, les éléments d’un tableau sont tous du même type (entier (int) ou réel (float)) et sa taille est fixe. On accède aux éléments d’un tableau avec un indice comme les listes

  1. tableau 1D: vecteurs

     np.array([0.,2.,1.]]
 np.zeros(N)

  2. tableau 2D: matrices avec 2 indices ligne puis colonne

     np.array([[2.,1.],[1.,2.]])

Attention par défaut opérations terme à terme

2.5. Coder de façon simple et lisible#

Un bon programme n’est pas uniquement fait pour etre exécuter par un ordinateur, mais surtout pour être compris par un humain !

  • syntaxe python

    • une instruction par ligne

    • indentation pour définir des blocs

    • aérer le code (utilisation des espaces)

2.6. Instructions conditionnelles#

important noté les : et l’indentation

  • valeur logique True et False

  • test logique

    if  condition :
   instruction 1
elif :
   instruction 2
else :
   instruction 3

2.7. instructions de répétition#

attention: on compte à partir de 0 en Python

important noté les : et l’indentation

  • boucle sur les valeurs d’une liste ou d’un tableau

    for val in Tab :
   instructions
   val = valeurs successives de Tab

  • boucle avec un compteur entier

    for i in range(n) :
   instructions
   i compteur de 0 à n (exclus)

  • boucle avec un compteur et une valeur

    for k, val in enumerate(Tab) :
   instructions
   k compteur de 0 à len(Tab) (exclus)
   val kieme valeur de Tab

  • boucle avec condition tant que (while)

     while condition :
   instructions
   on doit modifier la valeur de la condition, sinon boucle infinie

2.8. Fonction et algorithme#

C’est une bonne pratique de programmation d” éviter de répéter les instructions et d’écrire du code qui soit réutilisable, non seulement parce qu’il conduit à moins de temps de développement, mais aussi parce qu’il réduit les erreurs. Si vous devez faire le même calcul plusieurs fois, il vaut mieux l’encapsuler dans une fonction.

Rappelez-vous un des concepts clé de la programmation structurée :

  • Une fonction est une collection compacte de code qui exécute une action sur ses arguments ou données et qui renvoie le résultat.

  • Il faut déterminer les données, qui sont les arguments et le résultat qui est calculé et renvoyé avec return

  • Pour calculer le résultat, on peut créer des variables, qui sont des variables locales connues uniquement dans la fonction. C’est une bonne pratique de choisir des noms pour ces variables locales différents des autres variables globales.

  • Pour utiliser une fonction, on affecte à une variable le résultat de l’appel de la fonction en spécifiant la valeur des arguments

Une fois défini, vous pouvez appeler une fonction autant de fois que vous le souhaitez. Lorsque nous appelons une fonction, nous exécutons tout le code à l’intérieur de la fonction. Le résultat de l’exécution dépend de la définition de la fonction et des valeurs qui y sont passées en arguments. Les fonctions peuvent ou non renvoyer des valeurs lors de leur dernière opération.

La syntaxe pour définir ses propres fonctions est la suivante:

def nom_fonction (arg_1, arg_2, ...):
    '''
    docstring: description de la fonction
    '''
    <corps de la fonction>
    return valeur

Le docstring d’une fonction est un message du programmeur documentant ce qu’il a construit. Les docstrings doivent être descriptifs et concis. Ils sont importants car ils expliquent (ou rappellent) l’utilisation prévue de la fonction aux utilisateurs. Vous pouvez accéder ultérieurement à la docstring d’une fonction en utilisant la fonction help () et en passant le nom de la fonction. Si vous êtes dans un notebook, vous pouvez également ajouter un point d’interrogation ? avant le nom de la fonction et exécuter la cellule pour afficher les informations d’une fonction.

Pour appeler une fonction, on donne une valeurs aux arguments et on récupère le résultat, en général dans une variable:


# appel de la fonction 
resultat = nom_fonction(val1, val2, ..)

Lors de l’exécution de la fonction les arguments arg_1,arg_2 .. prennent respectivement la valeur val1, val2…

2.9. Lecture des données sur fichier#

Pour lire l’information dans un fichier au format texte, il faut effectuer les étapes suivantes:

  1. ouvrir le fichier en lecture en spécifiant son nom complet (i.e. avec le répertoire)

     F = open("nom complet du fichier","r")

  2. lire les données par exemple lignes par lignes, puis les décoder

     lignes = F.readlines()

  3. fermer le fichier

     F.close()

Pour des données stockés par colonnes dans un fichier, il existe une fonction simple numpy pour lire directement les valeurs: loadtxt()

     X,Y = loadtxt("nom fichier",unpack=True)

permet de lire directement les valeurs des 2 tableaux numpy X et Y stockés par colonne dans le fichier « nom fichier »

2.10. Tracé de résultats#

Pour tracer des courbes, on utilise la bibliothèque matplotlib et la fonction plt.plot

import matplotlib.pyplot as plt

Pour avoir un résultat de qualité, il faut ajouter un titre lisible, des labels sur les axes et sur les courbes:

  • plt.title

  • plt.xlabel, plt.ylabel

  • plt.legend

   X = [ k for k in range(n)]
   Y = [ sum(X[:k]) for k in range(n)]
   plt.plot(X,Y)

import matplotlib.pyplot as plt

n = 10
X = [ k for k in range(n)]
Y = [ sum(X[:k]) for k in range(n)]
# tracer basique
plt.plot(X,Y)

[<matplotlib.lines.Line2D at 0x7fb71e8f75b0>]
../../_images/e35db75f58509e481c349657fc51d5ecc705fc7b436b8c66a7fdc3b845ae6925.png 
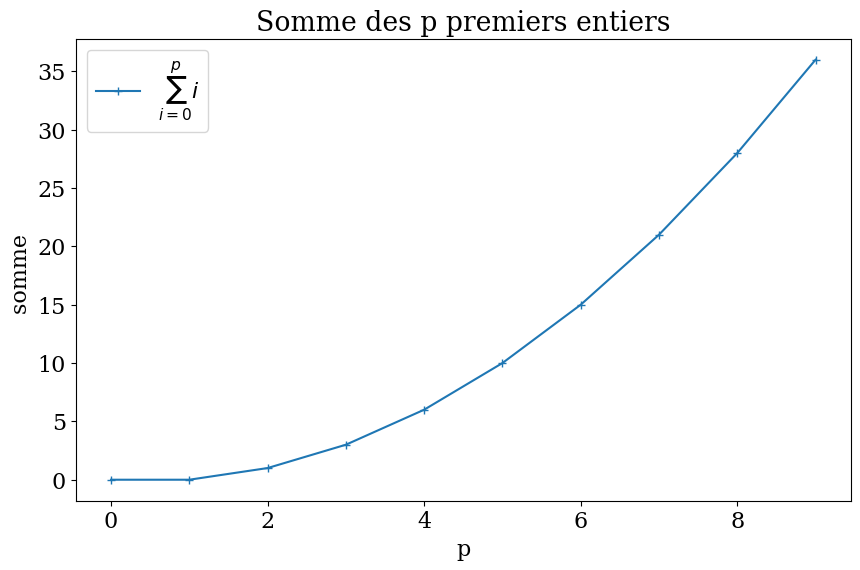
# tracer avec des titres
plt.rc('font', family='serif', size='16')
plt.figure(figsize=(10,6))
plt.plot(X,Y,'-+',label="$\sum_{i=0}^p i$")
plt.title("Somme des p premiers entiers")
plt.xlabel("p")
plt.ylabel("somme ")
plt.legend();
../../_images/dbfa2a32ec5528020c965a2ea6bd398ec2bcc4540931c54df4f94a09e75b26b8.png

2.11. Résumé#

  1. démarche scientifique

    • comprendre ce que l’on doit faire pour résoudre un problème et identifier en particulier

      • les données du problème

      • les résultats attendus

    • définir comment on va résoudre le problème (algorithmique)

    • choisir des cas de validation

  2. Algorithmique

    • notion de variables: élément essentiel pour faire des calculs et traiter les résultats

      • nom des variables (minuscule \(\neq\) majuscule)

      • type des variables (entier, caractère, réel)

    • structure de données: liste , tableau (numpy array)

    • index à partir de 0 (on compte à partir de 0)

      • X[i] élément du tableau X décalé de i par rapport au début

      • X[0] et X[-1]

    • notion de fonctions: définition d’un algorithme (indépendant)

      • nom

      • argument

      • valeur retournée

2.12. FIN de la leçon#

Contenu