6. TP mouvement du pendule double (solution)#
Marc BUFFAT, dpt mécanique, Université Lyon 1

Attention il faut exécuter la cellule vide suivante !!
%matplotlib inline
import numpy as np
import sympy as sp
from matplotlib import pyplot as plt
from IPython.display import display, Markdown, clear_output
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
from validation.validation import info_etudiant
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
printmd("**ERREUR**: numéro d'étudiant non spécifié!!!")
NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("Etudiant {} {} id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_alpha = sp.S(np.random.randint(1,5))/sp.S(np.random.randint(1,5))
_beta = sp.S(np.random.randint(1,5))/sp.S(np.random.randint(1,5))
_omega1 = sp.S(np.random.randint(2,6))
#
display("Parametres (alpha,beta,omega1)=",[_alpha,_beta,_omega1])
ERREUR: numéro d’étudiant non spécifié!!!
Etudiant Marc BUFFAT id=137764122
'Parametres (alpha,beta,omega1)='
[4/3, 3, 2]
%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from IPython.core.display import HTML
from IPython.display import display,Image
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, Particle
from sympy.physics.vector import vector
6.1. Modélisation mécanique#
On s’intéresse dans ce TP au mouvement non-linéaire du pendule double.
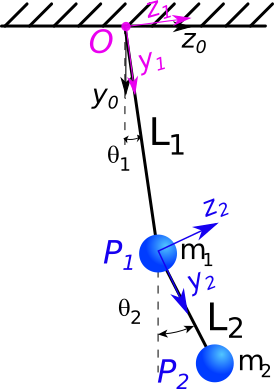
On reprend exactement les mêmes valeurs de paramêtres que pour le TP précedent du pendule double linéarisé.
Les equations du mouvement général obtenues précédement dans les variables Eq1et Eq2 sont données ci-dessous
Dans ce TP nous n’utiliserons que du calcul numérique et donc uniquement la bibliothéque numpy (pas de calcul symbolique avec sympy).
ATTENTION La partie analyse et commentaire est essentielle dans ce TP
l1, m1, l2, m2, g, t = sp.symbols('l_1 m_1 l_2 m_2 g t')
theta1, theta2 = dynamicsymbols('theta_1 theta_2')
O = Point('O')
R0 = ReferenceFrame('R_0')
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[theta1, R0.x])
P1 = Point('P_1')
P1.set_pos(O,l1*R1.y )
R2 = ReferenceFrame('R_2')
R2.orient(R0,'Axis',[theta2, R0.x])
P2 = Point('P_2')
P2.set_pos(P1,l2*R2.y )
O.set_vel(R0,0)
P1.set_vel(R1,0)
P2.set_vel(R2,0)
P1.v1pt_theory(O,R0,R1)
V2 = P2.v1pt_theory(P1,R0,R2).simplify()
P2.set_vel(R0,V2)
Pa1 = Particle('Pa_1',P1,m1)
Pa2 = Particle('Pa_2',P2,m2)
ma1 = Pa1.linear_momentum(R0).diff(t,R0).simplify()
ma2 = Pa2.linear_momentum(R0).diff(t,R0).simplify()
T1, T2 = sp.symbols('T_1 T_2')
F1 = m1*g*R0.y + T1*R1.y - T2*R2.y
F2 = m2*g*R0.y + T2*R2.y
eq1 = (ma1+ma2).dot(R1.z) - (F1+F2).dot(R1.z)
eq1 = (eq1/m2/l1).simplify().expand()
eq2 = ma2.dot(R2.z) - F2.dot(R2.z)
eq2 = (eq2/m2/l2).simplify().expand()
alpha, beta, omega1 = sp.symbols('alpha beta omega_1')
eq11 = eq1.subs([(g, omega1**2*l1),(m1,beta*m2),(l1,alpha*l2)])
eq11 = (eq11*alpha).simplify()
eq22 = eq2.subs([(g,alpha*omega1**2*l2),(l1,alpha*l2)])
vals = [(alpha,_alpha),(beta,_beta),(omega1,_omega1)]
Eq1 = eq11.subs(vals)
Eq2 = eq22.subs(vals)
print("Equations générales du mouvement du pendule double à étudier")
display(sp.Eq(Eq1,0))
display(sp.Eq(Eq2,0))
Equations générales du mouvement du pendule double à étudier
6.2. Simulation numérique#
Ecrire le système précédent sous la forme matricielle suivante:
définir la matrice M et le second membre B qui sont fonction de \([\theta_1, \theta_2, \dot{\theta_1}, \dot{\theta_2}]\)
Transformer le système d’EDO du second membre en un système du premier ordre avec un vecteur d’état \( \mathbf{Z} = [\theta_1, \theta_2, \dot{\theta_1}, \dot{\theta_2}]\) sous la forme
on définira \(\mathbf{K}\) (matrice 4x4) et \(\mathbf{Z}\) (vecteur 4) en fonction des composantes de \(\mathbf{Z}\)
Définir l’expression numériquement de \(\mathbf{K}\) (dans la variabe KK) et \(\mathbf{F}\) (dans la variable FF) dans la fonction double_pendule ci dessous en fonction du vecteur etat (qui correspond à z)
Ensuite pour déterminer \(\dot{\mathbf{Z}}\) dans la variable derivs , on résoud alors le système linaire
$\( \mathbf{K} \dot{\mathbf{Z}} = \mathbf{F}(\mathbf{Z})\)$
en utilisant la fonction np.linalg.solve() avec
derivs = np.linalg.solve(KK,FF)
Ecrire la fonction double_pendule pour calculer numeriquement ce second membre
def double_pendule(etat,temps=0): ''' calcul le second membre du système du double pendule Arguments --------- etat : vecteur d'etat [theta1,theta2,dtheta1,dtheta2] temps: instant t du calcul Retour ------- derivs: derivée du vecteur d'etat '''
6.2.1. CONSIGNES#
Vos commentaires et analyses doivent etre écrits dans les cellules de texte prévues (et uniquement dans ces cellules)
Pour vos calculs Python, écrire le code principal dans la cellule de code prévue, mais vous pouvez ajouter de nouvelles cellules de code, mais en commentant et expliquant votre démarche. Attention vous n’avez pas de cellules de validation, donc c’est à vous à valider vos calculs. Lorsque vous tracez des résultats, il faut absolument commenter vos figures: un figure sans commentaire, ni titre, ni explication est inutile!
Pour visualiser le mouvement vous pouvez utiliser la méthode d’animation proposée en fin de notebook identique à celle du notebook précédent. Pour cela il faut remplacer les tableaux Theta1 et Theta2 par les valeurs numériques que vous avez calculé.
display("Equations=",Eq1,Eq2)
'Equations='
from validation.Pendule_doubleNL import Pendule_doubleNL
pendule = Pendule_doubleNL(t,theta1,theta2,Eq1,Eq2)
'M='
'F='
def double_pendule(state,time=0):
global pendule
derivs = pendule.DerivZ(state)
return derivs
def rk2_step(state, rhs, time, dt):
'''Update a state to the next time increment using the RK2 method.
Arguments
---------
state : array of dependent variables
rhs : function that computes the RHS of the DE, taking (state, time)
time : float, time instant
dt : float, time increment
Returns
-------
next_state : array, updated after one time increment'''
mid_state = state + rhs(state,time) * dt*0.5
next_state = state + rhs(mid_state,time + 0.5*dt)*dt
return next_state
# trace sur n periode
omega = float(_omega1)
period = 2*np.pi/omega
dt = period/500
T = 10*period
N = round(T/dt)
tt = np.linspace(0, T, N)
# CI
theta0 = sp.pi/10
theta0 = sp.pi/4
theta0 = sp.pi/3
# cas NL
#theta0 = sp.pi/2
#theta0 = 4*sp.pi/5
#
#theta0 = sp.pi/20
display("CI theta0=",theta0)
'CI theta0='
# solution par la méthode RK2
num_solnl = np.zeros([N,4])
#Set intial conditions
num_solnl[0,0] = theta0.evalf()
num_solnl[0,1] = 0
num_solnl[0,2] = 0
num_solnl[0,3] = 0
print(rk2_step(num_solnl[0],double_pendule,0,dt))
[ 1.04712461e+00 4.86248001e-05 -2.32167948e-02 1.54788409e-02]
# calcul de la solution par RK2
for i in range(N-1):
num_solnl[i+1] = rk2_step(num_solnl[i], double_pendule, tt[i], dt)
#
plt.rc('font', family='serif', size='14')
Theta1_nl = num_solnl[:,0]
Theta2_nl = num_solnl[:,1]
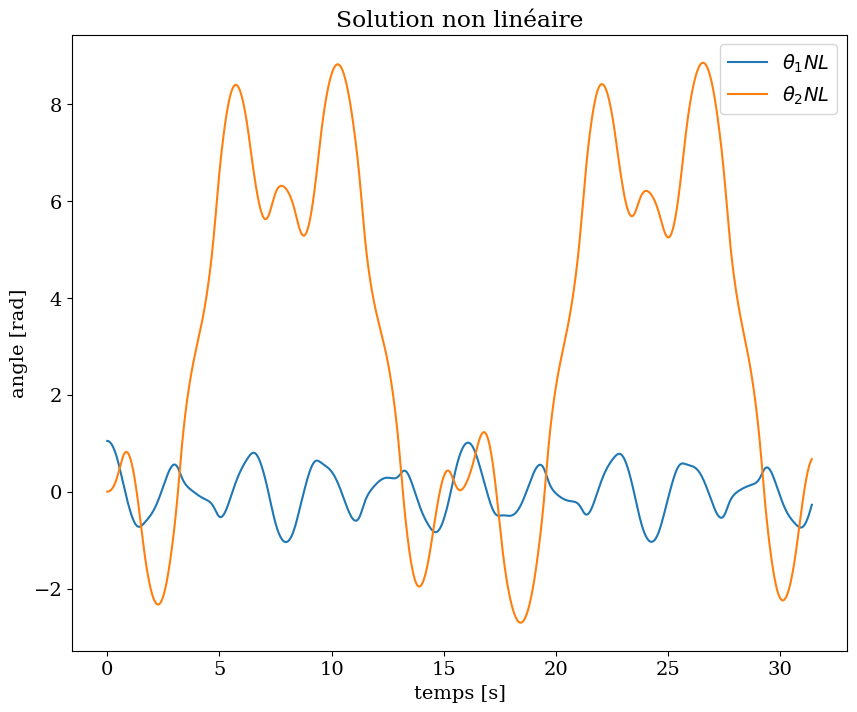
plt.figure(figsize=(10,8))
plt.plot(tt,Theta1_nl,label="$\\theta_1 NL$")
plt.plot(tt,Theta2_nl,label="$\\theta_2 NL$")
plt.legend()
plt.title("Solution non linéaire")
plt.ylabel("angle [rad]")
plt.xlabel("temps [s]");
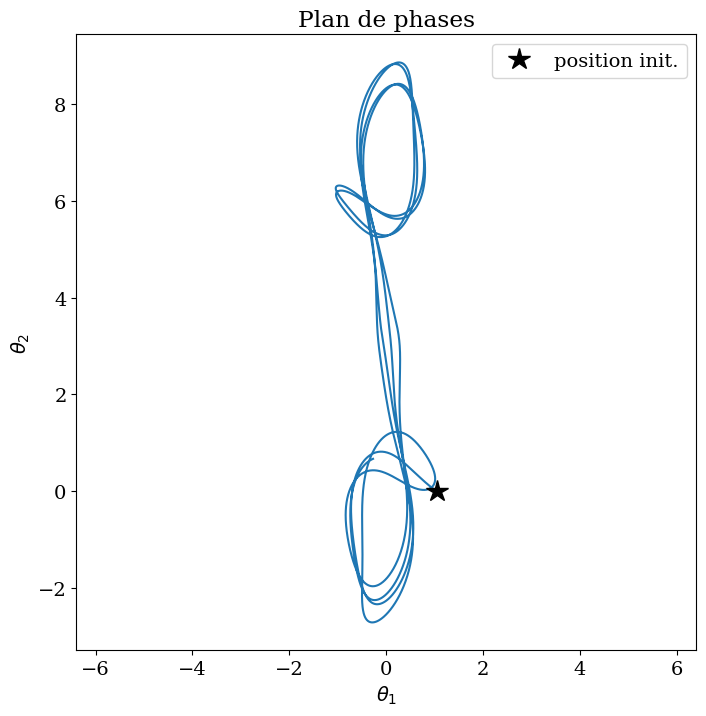
plt.figure(figsize=(8,8))
plt.plot(Theta1_nl,Theta2_nl)
plt.plot(Theta1_nl[0],Theta2_nl[0],'*',color='k',markersize=16,label='position init.')
plt.xlabel("$\\theta_1$")
plt.ylabel("$\\theta_2$")
plt.legend()
plt.axis('equal')
plt.title("Plan de phases");
# écrire vos calculs ici
### BEGIN SOLUTION
### END SOLUTION
6.2.2. Analyse sur la mise en équation et la modélisation numérique#
Ecrire votre analyse et commentaires ici en suivant le plan
6.2.2.1. Introduction#
6.2.2.2. description de la méthode d’étude#
6.2.2.3. Principe de la modélisation numérique#
6.3. Simulation numérique (validation)#
En reprenant le cas de petites oscillations, résoudre le problème avec la méthode d’itérations en temps de RungeKutta 2 et comparer avec la solution obtenu.
# ecrire vos calculs ici
### BEGIN SOLUTION
### END SOLUTION
6.3.1. Analyse sur la validation (cas linéaire)#
Ecrire votre analyse et commentaires ici en suivant le plan
6.3.1.1. justification du choix des conditions initiales#
6.3.1.2. comparaison avec la solution linéarisée#
6.3.1.3. propriétés de conservation#
6.4. Simulation numérique cas faiblement non linéaire#
En augmentant l’angle \(\theta_0\) initiale, effectuer plusieurs simulations pour observer le comportement du pendule dans le cas faiblement non linéaire.
On observera en particulier le comportement de la trajectoire dans le plan de phase \(\theta_1,\theta_2\)
# ecrire vos calculs ici
### BEGIN SOLUTION
### END SOLUTION
6.4.1. Analyse sur le cas faiblement non linéaire#
Ecrire votre analyse et commentaires ici en suivant le plan
6.4.1.1. description des similarités et différences avec le cas linéaire#
6.4.1.2. gamme des conditions initiales pour rester dans le cas faiblement non-liénaire#
6.5. Simulation numérique cas fortement non linéaire#
En augmentant encore l’angle \(\theta_0\) initiale, effectuer des simulations pour observer le comportement du pendule dans le cas fortement non linéaire et observer l’apparition de comportement chaotique
On observera en particulier le comportement de la trajectoire dans le plan de phase \(\theta_1,\theta_2\)
# ecrire vos calculs ici
### BEGIN SOLUTION
### END SOLUTION
6.5.1. Analyse sur le cas fortement non linéaire#
Ecrire votre analyse et commentaires ici
6.5.1.1. description et caractérisation du comportement chaotique#
6.5.1.2. gamme des conditions initiales pour obtenir un comportement chaotique#
6.6. Visualisation du mouvement: animation#
en utilisant la bibliothèque d’animation de matplotlib, on peut tracer la cinématique du mouvement.
Si on calcule l’évolution de \(\theta_1\) et \(\theta_2\) dans les tableaux numpy Theta1 et Theta, avec un pas en temps donné dans dt, on peut utiliser le code suivant pour visualiser le mouvement
Attention: le calcul de l’animation n’est pas instantané et il faut attendre un peu !
# exemple de calcul d'une solution données dans Theta1,Theta2
# à remplacer par votre propre solution numérique
Theta1 = Theta1_nl
Theta2 = Theta2_nl
if False:
print("initialisation")
omega1 = float(_omega1)
period = 2*np.pi/omega1
dt = period/500
T = 10*period
N = round(T/dt) + 1
tt = np.linspace(0, T, N)
theta0 = np.pi/6.
theta1 = np.pi/4.
Theta1 = theta0*np.cos(omega1*tt)
Theta2 = theta1*np.cos(omega1*tt)
from matplotlib import rc
from validation import Pendule_double
pendule_double = Pendule_double.Pendule_double(_alpha,_omega1)
# animation de solution numerique données dans Theta1,Theta2
pas = 4
pendule_double.solution(Theta1[::pas],Theta2[::pas],pas*dt)
anim = pendule_double.calculanim()
rc('animation', html='jshtml')
anim
