TP EDO: oscillations d’un système masse ressort

7. TP EDO: oscillations d’un système masse ressort#

Marc BUFFAT, dpt mécanique, Université Lyon 1

inspiré par le cours « Engineering Computations » du Pr L. Barba (Washington Univ.)

../../../../_images/spring-mass.png

Attention il faut exécuter la cellule vide suivante !!

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
from validation.valide_markdown import test_markdown, test_code
from validation.validation import info_etudiant, bib_validation, test_function
bib_validation('cours','MGC2028L')
from Oscillation import test1,test2,test3,test4,test5
from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_  = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("## Etudiant {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_omega0 = np.random.randint(1,15)
# systeme
_m  = np.round(0.1+2*np.random.rand(),2)
_k  = _m*_omega0**2
_x0 = np.round(5*(2*np.random.rand()-1),2)
_v0 = 0.
# forcage
_omega1  = _omega0/5
_A1 = np.round(_x0*_omega0**2*0.5*(0.1+np.random.rand()),1)
# mots clés
_mcl3_ = ['oscillation', 'forcage','période', 'erreur']
printmd("## parametres de l'étude:\n### Masse m={} [kg] raideur k={} [N/m]\n### Forcage: omega={} [rd/s], A={}[m/s^2]\n### CdtsInit: x0={}[m] v0={}[m/s]".format(_m,_k, _omega1, _A1, _x0, _v0))

try:
    printmd("INITIALISATION OK!")
except:
    print("Erreur vous n'avez pas executée la cellule vide précédente !")
    print("Votre Notebook n'est pas initialisé correctement !")

# bibliotheque
import numpy as np
from matplotlib import pyplot as plt
plt.rc('font', family='serif', size='14')

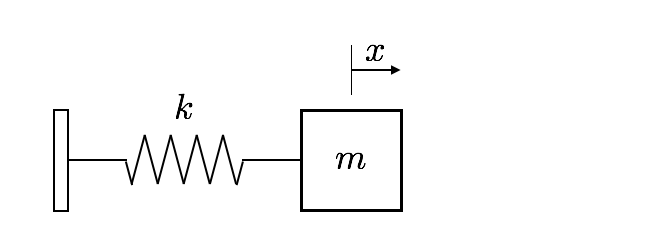
7.1. Contexte et principe de l’étude#

On se propose d’étudier un système mécanique modélisé par une masse \( m \) attachée à un ressort. Les valeurs des paramètres du problème ont été donnés au début du notebook.

7.1.1. Système masse ressort sans forcage#

Le système mécanique considéré est une masse \( m \) attachée à un ressort, dans le cas le plus simple sans frottement. La constante élastique du ressort, \( k \), détermine la force de rappel qu’il applique à la masse lorsqu’elle est déplacée d’une distance \( x \). Le système oscille alors d’avant en arrière autour de sa position d’équilibre

../../../../_images/spring-mass.png

dans la première partie du TP on déterminera le mouvement de ce système à partir d’une condition initiale donnée.

7.1.2. Système masse ressort avec forcage#

Dans une seconde partie on applique une force de forçage \(f_e(t)\) périodique sinusoidale de la forme:

\[f_e(t) = A m \cos(\omega t)\]

et on déterminera le mouvement du système dans ce cas

7.2. Compte rendu#

  1. éditer le fichier CompteRendu.md, puis générer la sortie html avec la commande ci-dessous. Cette commande se trouve en fin de notebook et doit être exécutée avant de soumettre le notebook de façon à bien générer la version html du rapport.

    # génération de la version html du CR
!genereTPhtml CompteRendu

  2. visualiser le fichier CompteRendu.html

dans ce compte rendu on demande de définir la démarche à utiliser et les différentes étapes pour réaliser cette modélisation, avec en particulier:

  • le problème à étudier et l’objectif

  • les calculs à faire

  • les fonctions python à écrire

  • l’analyse à faire

7.3. Etude du système simple masse ressort sans frottement et sans forcage#

La loi de Newton appliquée au système masse ressort sans frottement donne:

(7.1)#\[\begin{equation} -k x = m \ddot{x} \end{equation}\]

avec les conditions initiales: \(x(t=0)=x_0\) et \(\dot{x}(t=0)=0\)

Montrer que l’équation du mouvement peut s’écrire:

(7.2)#\[\begin{equation} \ddot{x} + \omega_0^2 x = 0 \end{equation}\]

On définiera le paramètre \(\omega_0\) (et son interprétation) et on justifiera dans le compte rendu que dans notre cas cette équation différentielle du second ordre possède une solution analytique qui représente un mouvement harmonique simple (dont on donnera les caractéristiques période, amplitude):

\[x(t) = x_0 \cos(\omega_0 t)\]

7.3.1. Mise sous forme vectorielle#

Pour résoudre numériquement une équation différentielle du second ordre, il faut tout d’abord la transformer en un un ensemble de deux équations du premier ordre: dans ce cas, respectivement pour la position et la vitesse:

(7.3)#\[\begin{eqnarray} \dot{x} &=& v \nonumber\\ \dot{v} &=& -\omega_0^2 x \end{eqnarray}\]

Comme vu en cours, nous écrivons l’état du système comme un vecteur \(Y(t)\),

(7.4)#\[\begin{equation} \mathbf{Y}(t) = \begin{bmatrix} x \\ v \end{bmatrix}, \end{equation}\]

et l’équation differentielle sous forme vectorielle:

(7.5)#\[\begin{equation} \dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y}(t),t) \mbox{ avec } \mathbf{F}(\mathbf{Y}(t),t) = \begin{bmatrix} v \\ -\omega_0^2 x \end{bmatrix}. \end{equation}\]

Écrire une fonction MasseRessort pour calculer le second membre \(F(Y(t))\) de ce système d’équations différentielles masse-ressort.

    MasseRessort(Y,t)

On définira la valeur de \(\omega_0\) du problème dans une variable globale omega0, pour pouvoir ensuite l’utiliser dans la fonction en le spécifiant dans la fonction

     global omega0

On vérifiera ensuite la fonction en l’appelant avec un vecteur d’état \(Y_0\) correspondant à \(x=0.1\) et \(v=0.0\) pour t=0.

On remarque que l’on passe le temps t comme second argument de la fonction même si \(Y\) ne dépend pas explicitement du temps, car on en aura besoin dans la suite pour traiter le cas avec un forcage

printmd("## parametres de l'étude:\n### Masse m={} [kg] raideur k={} [N/m]\n### Forcage: omega={} [rd/s], A={}[m/s^2]\n### CdtsInit: x0={}[m] v0={}[m/s]".format(_m,_k, _omega1, _A1, _x0, _v0))

# definition de omega0 et de la fonction MasseRessort
omega0 = 0
### BEGIN SOLUTION
### END SOLUTION

printmd("### Verification: appel de la fonction")
### BEGIN SOLUTION
### END SOLUTION

assert(test_code('TP_oscillation.ipynb','cell-verif1','MasseRessort('))
assert(np.abs(omega0/_omega0-1.0)<1.e-6)
assert(np.allclose(MasseRessort([1,1],0),[1,-omega0**2]))
assert(test_function(MasseRessort,test1,omega0))

7.3.2. Méthode d’Euler#

Pour résoudre numériquement l’EDO, on va tout d’abord utiliser la méthode d’Euler, qui consiste en une approximation du premier ordre qui permet de calculer la solution \(Y(t+dt)\) au temps \(t+dt\) en fonction de la solution connue \(Y(t)\) au temps \(t\)

\[ Y(t+dt) = Y(t) + dt \,F(Y(t),t) \]

Ecrire une fonction iterationEuler() qui calcule cette nouvelle solution en fonction de la solution courante Y, du second membre F, du pas en temps dt et du temps t

   iterationEuler(Y, F, dt, t)

On vérifiera ensuite la fonction en l’appelant avec un vecteur d’état \(Y_0\) correspondant à \(x=0.1\) et \(v=0.0\)

# fonction iterationEuler
## BEGIN SOLUTION
## END SOLUTION

printmd("### Verification: appel de la fonction")
### BEGIN SOLUTION
### END SOLUTION

assert(test_code('TP_oscillation.ipynb','cell-verif1a',['MasseRessort','iterationEuler(']))
assert(test_function(iterationEuler,test2,MasseRessort))

7.3.3. Méthode de Runge Kutta 2#

Pour améliorer la précision de la solution numérique, on utilise une méthode de RungeKutta 2 qui utilise une estimation au second ordre en calculant la dérivée au milieu de l’intervalle:

\[ Y(t+dt) = Y(t) + dt\,F(Y(t+\frac{dt}{2}), t+\frac{dt}{2} ) \]

Mais cette dérivée \(F(Y(t+dt/2))\) dépend de la valeur de l’état en \(t+dt/2\) (qui n’est pas connu, car on ne connait que \(Y(t)\)) et que l’on estime avec la méthode d’Euler précédente:

\[ Y(t+\frac{dt}{2}) = Y(t) + \frac{dt}{2} F(Y(t),t) \]

au milieu d’un intervalle de temps avec la méthode d’Euler, en y calculant les dérivées, puis en revenant en arrière et en mettant à jour l’état du système en utilisant les dérivées du point médian. C’est ce qu’on appelle une méthode de Runge Kutta 2.

La méthode numérique de Runge Kutta 2 s’écrit sous forme matricielle:

(7.6)#\[\begin{align} \mathbf{Y}(t+\frac{dt}{2}) & = \mathbf{Y}(t) + \frac{dt}{2} \mathbf{F}(\mathbf{Y}(t),t) \\ \mathbf{Y}(t+dt) & = \mathbf{Y}(t) + dt \,\, \mathbf{F}(\mathbf{Y}(t+\frac{dt}{2}),t+\frac{dt}{2}). \end{align}\]

Ecrire une fonction iterationRK2() qui calcule cette nouvelle solution en fonction de la solution courante Y, du second membre F, du pas en temps dt et du temps t:

   iterationRK2(Y, F, dt, t)

On vérifiera ensuite la fonction en l’appelant avec un vecteur d’état \(Y_0\) correspondant à \(x=0.1\) et \(v=0.0\)

attention spécifier bien la bonne valeur du temps lors de l’appel de la fonction \(F\)

# fonction iterationRK2
### BEGIN SOLUTION
### END SOLUTION

printmd("### Verification: appel de la fonction")
### BEGIN SOLUTION
### END SOLUTION

assert(test_code('TP_oscillation.ipynb','cell-verif1b',['MasseRessort','iterationRK2(']))
assert(test_function(iterationRK2,test3,MasseRessort))

7.3.4. Définition des paramètres#

Nous définissons les paramètres du système, choisissons un intervalle de temps égal à 1/100e de la période d’oscillation, et décidons de résoudre le mouvement pour une durée tfin égale à 10 périodes.

Calculer la valeur du pas en temps dt, la durée de simulation tfin, le vecteur T des temps de 0 a tfin et la dimension N de T.

Ensuite, on doit définir les conditions initiales, et le tableau des solutions en initialisant avec des valeurs nulles. On définira 2 tableaux de solutions: le premier sol_num pour le calcul avec la méthode d’Euler et le second sol_num2 pour le calcul avec RungeKutta 2

  • Définir les tableau des solutions sol_num et sol_num2 (de dimension (N,2))

  • Definir la valeur initiale x0 et v0

# parametres
dt = 0
T = None
N = 0
tfin = 0
#initialisation du tableau des solutions
x0 = 0
v0 = 0
sol_num = None
sol_num2 = None
### BEGIN SOLUTION
### END SOLUTION

assert(np.abs(omega0*tfin-20*np.pi)<1.e-6)
assert(np.abs(tfin - (N-1)*dt) < 1.e-3)
assert(T.size == N)
assert((sol_num.size == 2*N) and (sol_num2.size == 2*N))

7.3.5. Simulation#

Nous sommes maintenant prêts à résoudre le problème!

En parcourant les incréments de temps, on va calculer la solution à l’étape i+1 en appelant soit la fonction iterationEuler() soit la fonction iterationRK2() avec comme argument la solution à l’étape i, la fonctionMasseRessort (qui calcule le second membre de l’EDO) et l’incrément de temps comme entrées

Il faut appliquer la CI dans les tableaux sol_num et sol_num2 pour définir la première valeur du tableau.

Ecrire les itérations en temps dans la cellule suivante pour calculer les valeurs de sol_num et les valeurs de sol_num2

# iteration en temps
### BEGIN SOLUTION
# initial conditions
### END SOLUTION

assert((np.allclose(sol_num[0],[_x0,_v0]) == True) and (np.allclose(sol_num2[0],[_x0,_v0]) == True))
assert(test_code('TP_oscillation.ipynb','cell-verif1c',['iterationEuler(','iterationRK2(']))

7.3.6. Solution analytique#

Maintenant, calculons la position en fonction du temps en utilisant la solution analytique connue, afin de la comparer avec le résultat numérique. Puis nous traçons sur un graphique à la fois des valeurs numériques et analytiques.

  • définir dans la variable x_an la solution analytique vérifiant les CI pour tous les instant dans t

# solution analytique
x_an = None
### BEGIN SOLUTION
### END SOLUTION

assert(x_an.size == N)
assert(np.allclose(x_an[0],[_x0]) == True)
assert(np.abs((4*x_an[1]-3*x_an[0]-x_an[2])/(2*dt) - v0) < 0.3)

7.3.7. Comparaison avec la solution analytique#

dans la cellule suivante, comparer les 2 solutions numériques avec la solution analytique en traçant les courbes, et en calculant la norme de l’erreur entre la solution numérique et la solution analytique

\[ || x_num - x_an || \mbox{ et } || x_num2 - x_an || \]

Pour calculer cette norme, on pourra utiliser la fonction numpy suivante pour calculer la norme d’un vecteur X en normalisant par la dimension de X

np.linalg.norm(X)/X.size

On analysera le résultat dans le compte rendu. On pourra en particulier refaire le calcul avec un pas en temps 2 fois plus petit et commenter l’évolution de l’erreur (en donnant l’ordre de grandeur de la diminution de l’erreur).

# plot solution with Euler's method
### BEGIN SOLUTION
### END SOLUTION

assert(test_code("TP_oscillation.ipynb","cell-verif1d",["plt.plot","plt.legend","plt.title"]))
assert(np.abs(sol_num2[-1,0]-x_an[-1]) < np.abs(0.1*x_an[-1]))

7.4. Etude du cas avec forçage sinusoidal#

Supposons maintenant qu’une force externe de la forme \(F(t) = A m \cos(\omega t)\) excite le système.

La loi de Newton appliquée au système donne:

(7.7)#\[\begin{equation} -k x = m \ddot{x} + F(x) \end{equation}\]

avec les conditions initiales: \(x(t=0)=x_0\) et \(\dot{x}(t=0)=0\)

Montrer que l’équation du mouvement peut s’écrire:

(7.8)#\[\begin{equation} \ddot{x} + \omega_0^2 x = A \cos(\omega t) \end{equation}\]

En déduire la nouvelle forme du système de 2 équations différentielles à résoudre pour pouvoir utiliser la méthode de RK2.

Pour cela il faut écrire une nouvelle fonction MasseRessortForcage fonction de \(Y\) et t

  MasseRessortForcage(Y,y)

printmd("## parametres de l'étude:\n### Masse m={} [kg] raideur k={} [N/m]\n### Forcage: omega={} [rd/s], A={}[m/s^2]\n### CdtsInit: x0={}[m] v0={}[m/s]".format(_m,_k, _omega1, _A1, _x0, _v0))

# fonction MasseRessortForcage
omega = 0
A = 0
## BEGIN SOLUTION
### END SOLUTION

printmd("### Verification: appel de la fonction")
### BEGIN SOLUTION
### END SOLUTION

assert((A==_A1) and (omega==_omega1))
assert(test_code('TP_oscillation.ipynb','cell-verif3','MasseRessortForcage('))
assert(test_function(MasseRessortForcage,test4,[omega0,A,omega]))

7.4.1. Définition des paramètres#

Nous définissons les paramètres du système, et choisissons les mêmes paramètres que précédemment pour pouvoir comparer.

On définira le tableau de solutions sol_f2 pour un calcul avec la méthode RungeKutta 2

# parametres
sol_f2 = None
### BEGIN SOLUTION
### END SOLUTION

assert(sol_f2.size == 2*N)

7.4.2. Simulation#

Nous sommes maintenant prêts à résoudre le problème!

En utilisant la même approche que précédemment, écrire les itérations en temps dans la cellule suivante pour calculer les valeurs de sol_f2

# iteration en temps
### BEGIN SOLUTION
# initial conditions
### END SOLUTION

assert((np.allclose(sol_f2[0],[_x0,_v0]) == True))
assert(test_code('TP_oscillation.ipynb','cell-verif3c',['MasseRessortForcage','iterationRK2(']))
assert(test_function(sol_f2,test5,[iterationRK2,MasseRessortForcage,x0,v0,dt]))

7.4.3. Analyse de la solution#

Tracer sur une même figure le résultat de la simulation avec et sans forcage, et commenter le résultat dans le compte rendu.

# tracer de la solution
## BEGIN SOLUTION
## END SOLUTION

assert(test_code("TP_oscillation.ipynb","cell-verif3d",["plt.plot","plt.legend","plt.title"]))

7.5. Analyse du cas avec forcage#

Pour analyser la solution, on pourra déterminer la forme de la solution générale de l’équation différentielle d’ordre 2 avec second membre en cherchant une solution particulière sous la forme \(\alpha \cos(\omega t)\).

On pourra aussi regarder l’allure des courbes de la forme \(\cos(2t)+\cos(10t)\) (en les traçant).

A partir de ces éléments, expliquez le mouvement du système avec le forçage choisi.

7.6. Compte rendu#

Ecrire votre analyse et votre conclusion dans le compte rendu en insistant sur

  1. Description de la méthode d’analyse

  2. Résultat de l’analyse

  3. Conclusion

Le compte rendu est à écrire dans le fichier CompteRendu.md

  1. Génération de la version HTML du Compte Rendu (avec mise en page)

  • Exécution de la commande ci-dessous pour générer le fichier html

  1. Visualisation du Compte Rendu (version html)

  • Cliquez sur le lien suivant après exécution de la commande ci-dessous

  • Cliquez sur le bouton mise à jour du navigateur pour mettre à jour la page web

# génération de la version html du CR
!genereTPhtml CompteRendu

# test sur les commentaires (a executer)
assert(test_markdown('CompteRendu.md',None,minm=200,maxe=0.25,mcl=_mcl3_ ,maxs=0.72))

7.7. FIN du TP#

# version
from platform import python_version,uname,platform
print("Systeme       :",uname())
print("OS            :",platform())
print("version python:",python_version())
print("version numpy :",np.__version__)
Contenu