2. Cinématique et Trajectoires

Marc BUFFAT département mécanique, université Lyon 1

%matplotlib inline
import numpy as np
import sympy as sp
from sympy.plotting import plot
import matplotlib.pyplot as plt
# police des titres
plt.rc('font', family='serif', size='18')
from IPython.core.display import HTML
from IPython.display import display
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, RigidBody
from sympy.physics.vector import dot
from metakernel import register_ipython_magics
register_ipython_magics()

2.1. Dérivée d’un vecteur

soit \(\vec{U}\) un vecteur de \(R^3\), on veut calculer sa dérivée par rapport au temps

On connaît les composantes du vecteur dans un référentiel de base \(\vec{e}_1, \vec{e}_2, \vec{e}_3\) du référentiel $\( \vec{U} = u_1 \vec{e}_1 + u_2 \vec{e}_2 + u_3 \vec{e}_3\)$

2.1.1. dérivée d’un vecteur dans \(R^3\)

• on décompose le vecteur sur la base \(\vec{e}_1, \vec{e}_2, \vec{e}_3\) du référentiel

\[ \vec{U} = u_1 \vec{e}_1 + u_2 \vec{e}_2 + u_3 \vec{e}_3\]

• calcul de la dérivée

\[ \frac{d}{dt} \vec{U} = \dot{u}_1 \vec{e}_1 + \dot{u}_2 \vec{e}_2 + \dot{u}_3 \vec{e}_3 + u_1 \frac{d}{dt}\vec{e}_1 + u_2 \frac{d}{dt}\vec{e}_2 + u_3 \frac{d}{dt}\vec{e}_3 \]

2.2. Cinématique (étude du mouvement)

soit \(M(t)\) un point matériel dont les coordonnées dans un référentiel fixe \(R_0\) (mouvement plan)

\[ \vec{OM} = x_m(t) \vec{e_x} + y_m(t) \vec{e_y} \]

dont la vitesse / \(R_0\)

\[ \vec{V}(M) = \frac{d\vec{OM}}{dt} = \dot{x}_m \vec{e_x} + \dot{y}_m \vec{e_y} \]

L’accélération est donnée par

\[ \vec{G}(M) = \frac{d\vec{V}(M)}{dt} = \ddot{x}_m \vec{e_x} + \ddot{y}_m \vec{e_y} \]

# mouvement plan
t = sp.symbols('t')
xm,ym = dynamicsymbols('x_m y_m')
R0 = ReferenceFrame("R_0")
O = Point("O")
O.set_vel(R0,0)
M = Point("M")
M.set_pos(O, xm*R0.x + ym*R0.y )
display("OM=",M.pos_from(O))
display("V(M)=",M.vel(R0))
display("G(M)=",M.acc(R0))

'OM='

\[\displaystyle x_{m}{\left(t \right)}\mathbf{\hat{r_0}_x} + y_{m}{\left(t \right)}\mathbf{\hat{r_0}_y}\]

'V(M)='

\[\displaystyle \frac{d}{d t} x_{m}{\left(t \right)}\mathbf{\hat{r_0}_x} + \frac{d}{d t} y_{m}{\left(t \right)}\mathbf{\hat{r_0}_y}\]

'G(M)='

\[\displaystyle \frac{d^{2}}{d t^{2}} x_{m}{\left(t \right)}\mathbf{\hat{r_0}_x} + \frac{d^{2}}{d t^{2}} y_{m}{\left(t \right)}\mathbf{\hat{r_0}_y}\]

2.3. Trajectoire circulaire:

1. rotation de la terre autour de son axe: mouvement d’un point sur la terre

2. mouvement de la terre/ soleil: modèle simplifié d’une planéte (mouvement héliocentrique de Copernic)

2.3.1. Mise en équations

• cercle de rayon a

\[ (\frac{x}{a})^2 + (\frac{y}{a})^2 = 1 \]

• mouvement uniforme de taux de rotation \(\omega\)

  \[ x(t) = a \cos\omega t \mbox{ et } y(t) = a \sin\omega t \]

• vitesse

  \[ \dot{x}(t) = -a \omega \sin\omega t \mbox{ et } \dot{y}(t) = a \omega \cos\omega t \]

• accélération

  \[ \ddot{x}(t) = -a \omega^2\cos\omega t \mbox{ et } \ddot{y}(t) = -a\omega^2 \sin\omega t \]

a,omega = sp.symbols('a omega')
# trajectoire circulaire
ValNum={a:4, omega:2*sp.pi}
display(ValNum)
# position de M 
re = a.subs(ValNum)
xp = re*sp.cos(omega*t).subs(ValNum)
yp = re*sp.sin(omega*t).subs(ValNum)
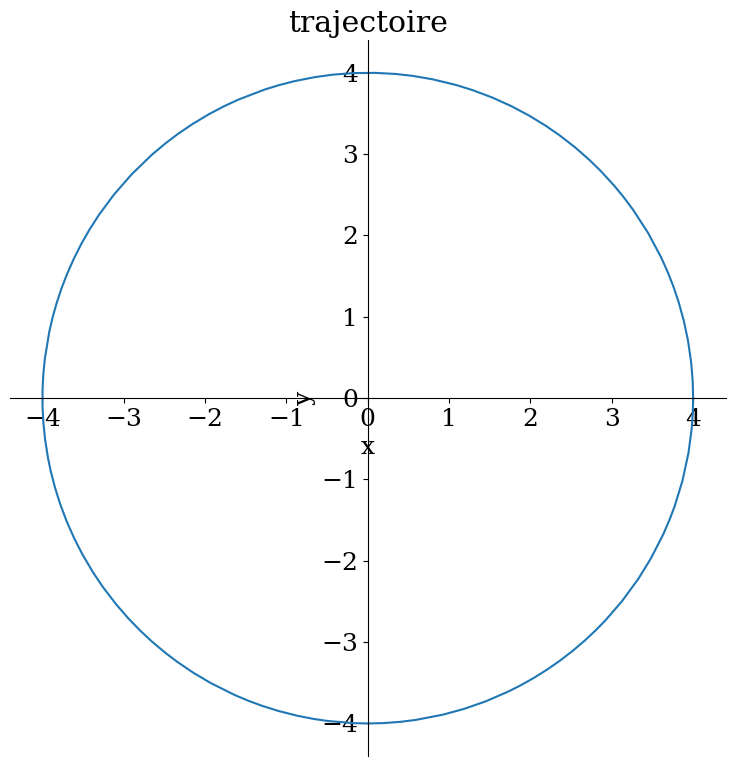
# tracer
tmax = 1
p1 = sp.plot_parametric(xp,yp,(t,0,tmax), show=False, size=(10,8), xlabel='x',ylabel='y',title="trajectoire")
p1.aspect_ratio=(1,1)
p1.show()

{a: 4, omega: 2*pi}

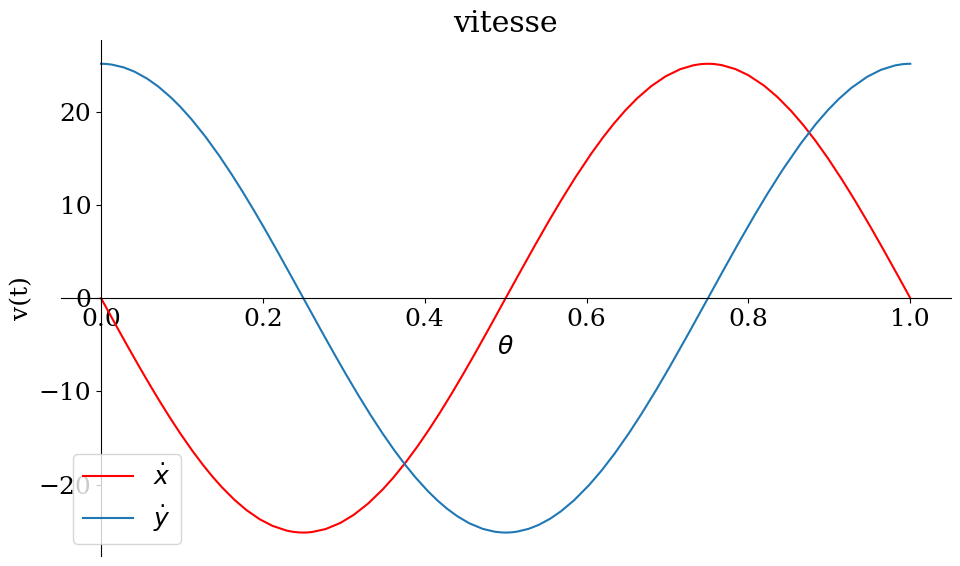
2.3.2. Vitesse

P = Point("P")
P.set_pos(O,xp*R0.x + yp*R0.y)
# calcul de la vitesse
dxp = xp.diff(t)
dyp = yp.diff(t)
display("V=",dxp,dyp)
p1 = sp.plot(dxp,dyp,(t,0,tmax),show=False,size=(10,6),xlabel='$\\theta$',ylabel='v(t)',title="vitesse",legend=True)
p1[0].line_color='r'
p1[0].label='$\dot{x}$'
p1[1].label='$\dot{y}$'
p1.show()

'V='

\[\displaystyle - 8 \pi \sin{\left(2 \pi t \right)}\]

\[\displaystyle 8 \pi \cos{\left(2 \pi t \right)}\]

sp.plot(sp.sqrt(dxp**2+dyp**2),(t,0,tmax),title="amplitude vitesse",ylabel="|u|",size=(10,6),line_color='r');

THETA = np.linspace(0,tmax,101)
Xm = sp.lambdify(t,xp)
Ym = sp.lambdify(t,yp)
Um = sp.lambdify(t,dxp)
Vm = sp.lambdify(t,dyp)
plt.figure(figsize=(12,8))
plt.plot(Xm(THETA),Ym(THETA))
plt.quiver(Xm(THETA)[::4],Ym(THETA)[::4],Um(THETA)[::4],Vm(THETA)[::4])
plt.plot([0],[0],'o',markersize=18)
plt.title("Trajectoire et vitesse")
plt.axis('equal');

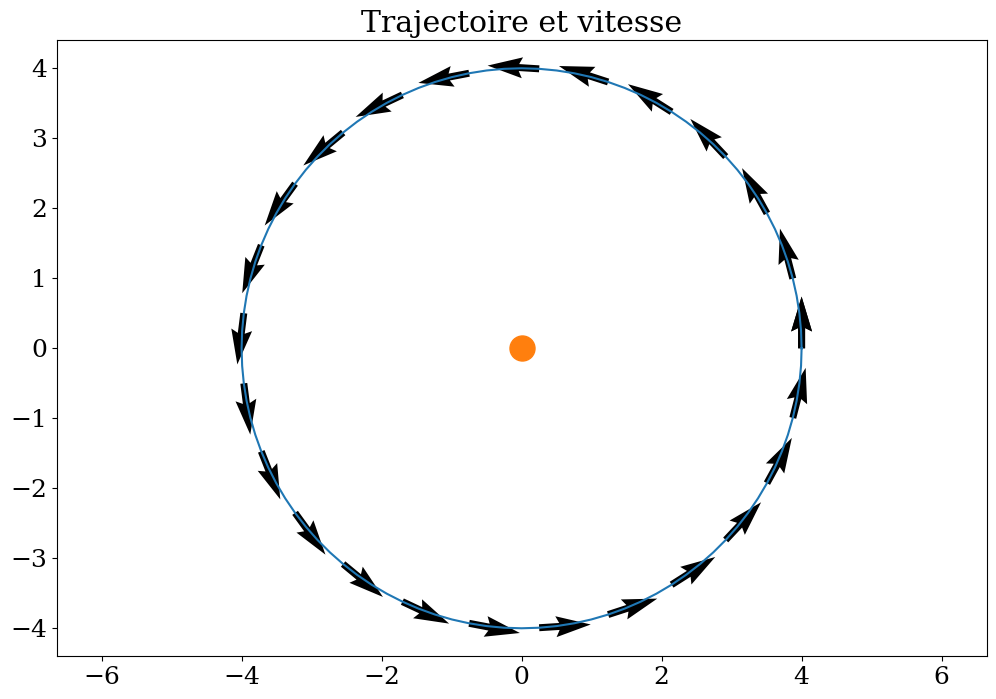
2.3.3. Réponses aux questions

1. la vitesse est-elle constante ?

2. le module de la vitesse est-il constant ?

3. si non ou est le minimum ? le maximum ?

4. quelle est la direction de la vitesse ?

2.3.4. Accélération

# calcul de l'acceleration
d2xp = dxp.diff(t)
d2yp = dyp.diff(t)
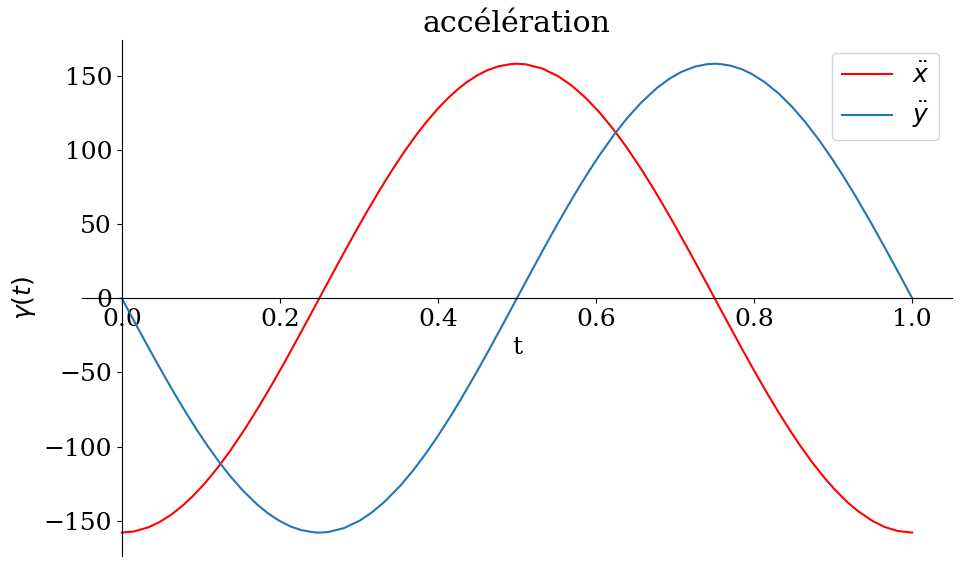
p1 = sp.plot(d2xp,d2yp,(t,0,tmax),show=False,size=(10,6),xlabel='t',ylabel='$\gamma(t)$',title="accélération",
            legend=True)
p1[0].line_color='r'
p1[0].label='$\ddot{x}$'
p1[1].label='$\ddot{y}$'
p1.show()

Xm = sp.lambdify(t,xp)
Ym = sp.lambdify(t,yp)
Gxm = sp.lambdify(t,d2xp)
Gym = sp.lambdify(t,d2yp)
plt.figure(figsize=(12,8))
plt.plot(Xm(THETA),Ym(THETA))
plt.quiver(Xm(THETA)[::4],Ym(THETA)[::4],Gxm(THETA)[::4],Gym(THETA)[::4])
plt.title("Trajectoire et accélération")
plt.plot([0],[0],'o',markersize=18)
plt.axis('equal');

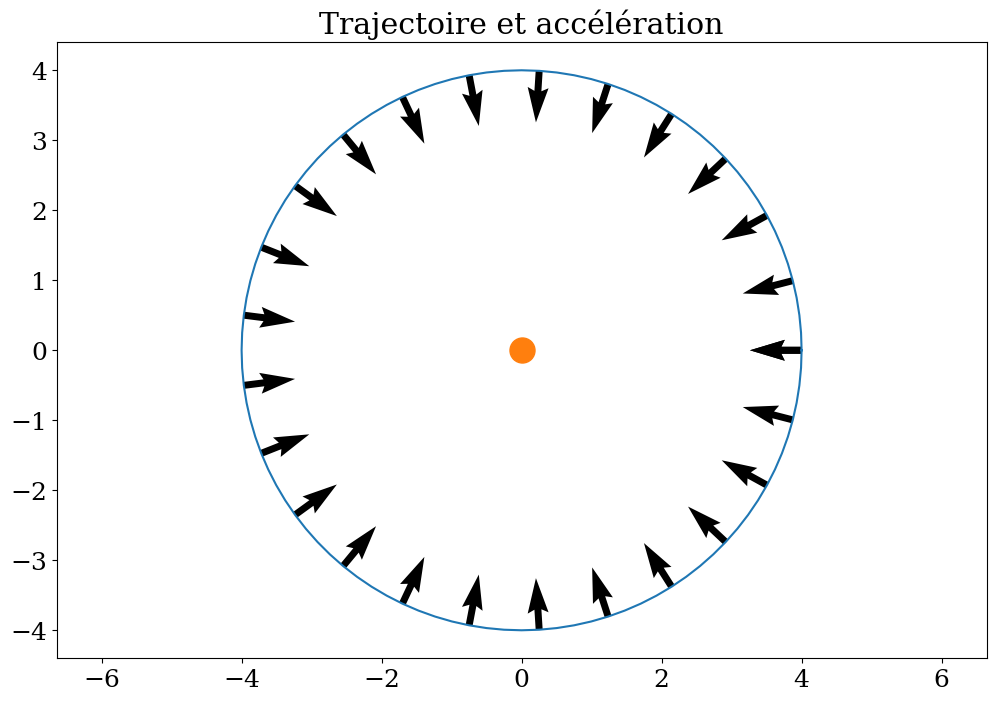
2.3.5. Réponses aux questions

1. l’accélération est-elle constante ?

2. le module de l’accélération est-il constant ?

3. si non ou est le minimum ? le maximum ?

4. quelle est la direction de l’accélération

2.4. Trajectoire elliptique

Mouvement héliocentrique des planétes de Kepler

• a,b axes de l’ellipse x,y coordonnées / centre O

\[xp = a \cos{\theta} \mbox{ et } yp = b \sin{\theta} \]

• trajectoire = ellipse de rayon \(a,b\) avec \(a>b>0\)

\[ (\frac{x}{a}]^2 + (\frac{y}{b})^2 = 1\]

• distance \(c\) du foyer au centre

\[ c = \sqrt{a^2 - b^2} \]

• équation de l’ellipse / au foyer de l’ellipse (soleil)

\[ (\frac{x+c}{a})^2 + (\frac{y}{a})^2 = 1 \]

avec \(c = \sqrt{a^2-b^2}\)

• excentricité \(e = \frac{c}{a}\)

• paramètre ellipse \(p=\frac{b^2}{a}\)

• équation polaire de l’ellipse / au foyer de l’ellipse (soleil): rayon par rapport au foyer

\[ r_e = \frac{p}{1-e \cos{\theta}} \]

Loi des aires: 2nde loi de Kepler

Les planétes décrivent des ellipses et le soleil se trouve sur un des foyers (périhélie)

Soit \(A(t)\) l’aire de la surface balayée par le rayon vecteur \(r_e\) durant le mouvement d’une planète, alors cette seconde loi stipule que des aires égales sont balayées dans des temps égaux.

La loi des aires impose la variation de l’angle en fonction du temps:

\[\frac{1}{2} r_e^2 d\theta = cste\]

ce qui implique:

\[\dot{\theta} = r_e^{-2}\]

a,b,c,e,p,theta= sp.symbols('a b c e p theta')
# trajectoire ellipse
ValNum={a:5, b:3}
ValNum['c'] = sp.sqrt(a**2-b**2).subs(ValNum)
ValNum['e'] = (c/a).subs(ValNum)
ValNum['p'] = (b**2/a).subs(ValNum)
display(ValNum)
# position de M / Foyer
re = (p/(1-e*sp.cos(theta))).subs(ValNum)
xp = re*sp.cos(theta).subs(ValNum)
yp = re*sp.sin(theta).subs(ValNum)
display("re=",re)
# tracer
tmax = 2*sp.pi
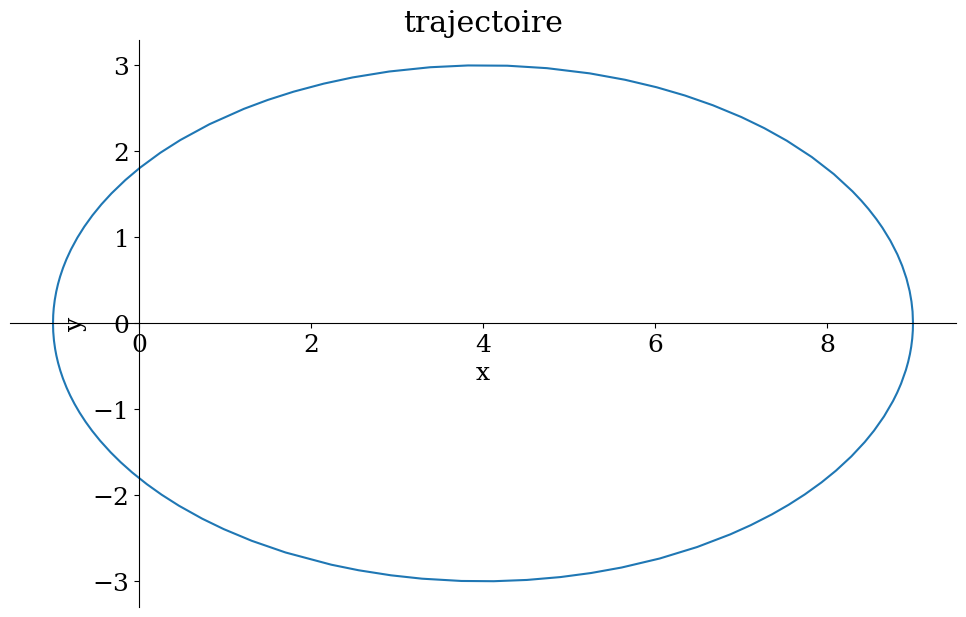
p1 = sp.plot_parametric(xp,yp,(theta,0,tmax), show=False, size=(10,8), xlabel='x',ylabel='y',title="trajectoire")
p1.aspect_ratio=(1,1)
p1.show()

{a: 5, b: 3, 'c': 4, 'e': 4/5, 'p': 9/5}

're='

\[\displaystyle \frac{9}{5 \cdot \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)}\]

# dt = r^2 dtheta
te = sp.integrate(re**2).simplify()
te = te - te.subs(theta,0)
display(te)
sp.plot(te,(theta,0,tmax),xlabel="$\\theta$",ylabel='t',title="$t=t(\\theta)$", size=(10,6))

\[\displaystyle 30 \pi + \frac{6 \cdot \left(45 \left(\operatorname{atan}{\left(3 \tan{\left(\frac{\theta}{2} \right)} \right)} + \pi \left\lfloor{\frac{\theta}{2 \pi} - \frac{1}{2}}\right\rfloor\right) \tan^{2}{\left(\frac{\theta}{2} \right)} + 12 \tan{\left(\frac{\theta}{2} \right)} + 5 \operatorname{atan}{\left(3 \tan{\left(\frac{\theta}{2} \right)} \right)} + 5 \pi \left\lfloor{\frac{\theta - \pi}{2 \pi}}\right\rfloor\right)}{9 \tan^{2}{\left(\frac{\theta}{2} \right)} + 1}\]

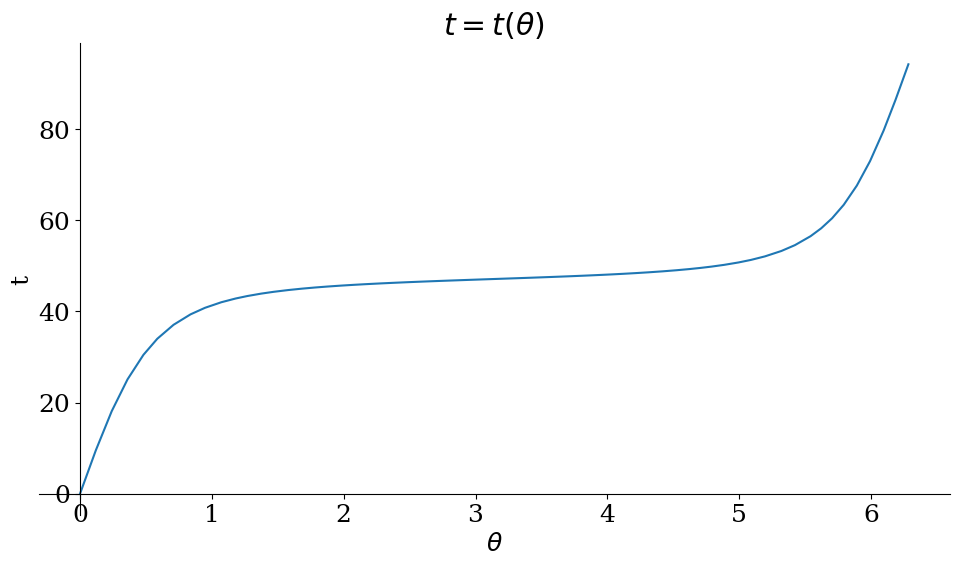
<sympy.plotting.plot.Plot at 0x7f1b79276950>

sp.plot(1/re**2,(theta,0,tmax),xlabel="$\\theta$", ylabel="$\dot{\\theta}$")

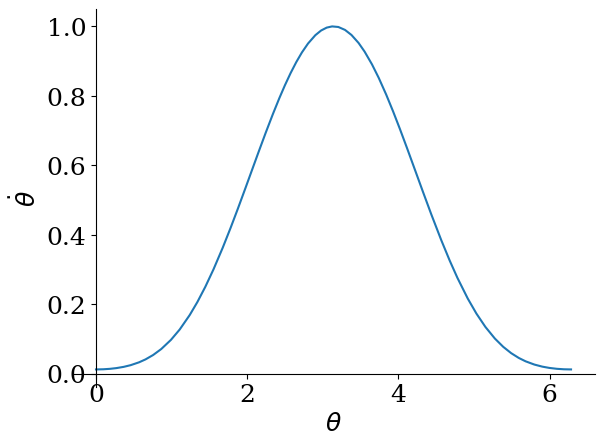
<sympy.plotting.plot.Plot at 0x7f1b792364a0>

tn = sp.lambdify([theta],te)
rn = sp.lambdify([theta],re)
THETA = np.linspace(0,2*np.pi,101)
DTHETA= rn(THETA)**(-2)
T = tn(THETA)

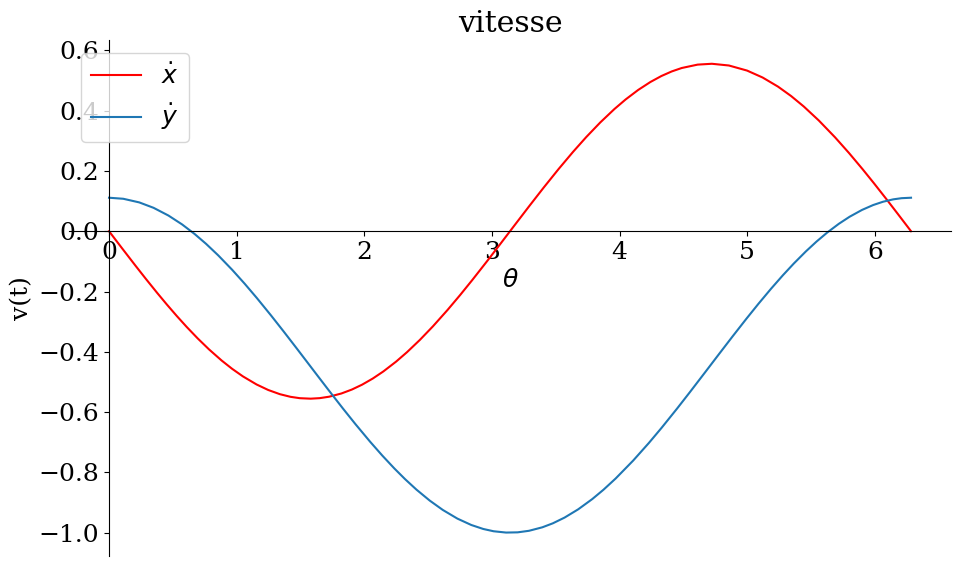
2.4.1. Vitesse

P = Point("P")
P.set_pos(O,xp*R0.x + yp*R0.y)
# calcul de la vitesse
dxp = xp.diff(theta)/re**2
dyp = yp.diff(theta)/re**2
display("V=",dxp,dyp)
p1 = sp.plot(dxp,dyp,(theta,0,tmax),show=False,size=(10,6),xlabel='$\\theta$',ylabel='v(t)',title="vitesse",legend=True)
p1[0].line_color='r'
p1[0].label='$\dot{x}$'
p1[1].label='$\dot{y}$'
p1.show()

'V='

\[\displaystyle \frac{25 \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)^{2} \left(- \frac{9 \sin{\left(\theta \right)}}{5 \cdot \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)} - \frac{36 \sin{\left(\theta \right)} \cos{\left(\theta \right)}}{25 \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)^{2}}\right)}{81}\]

\[\displaystyle \frac{25 \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)^{2} \cdot \left(\frac{9 \cos{\left(\theta \right)}}{5 \cdot \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)} - \frac{36 \sin^{2}{\left(\theta \right)}}{25 \left(1 - \frac{4 \cos{\left(\theta \right)}}{5}\right)^{2}}\right)}{81}\]

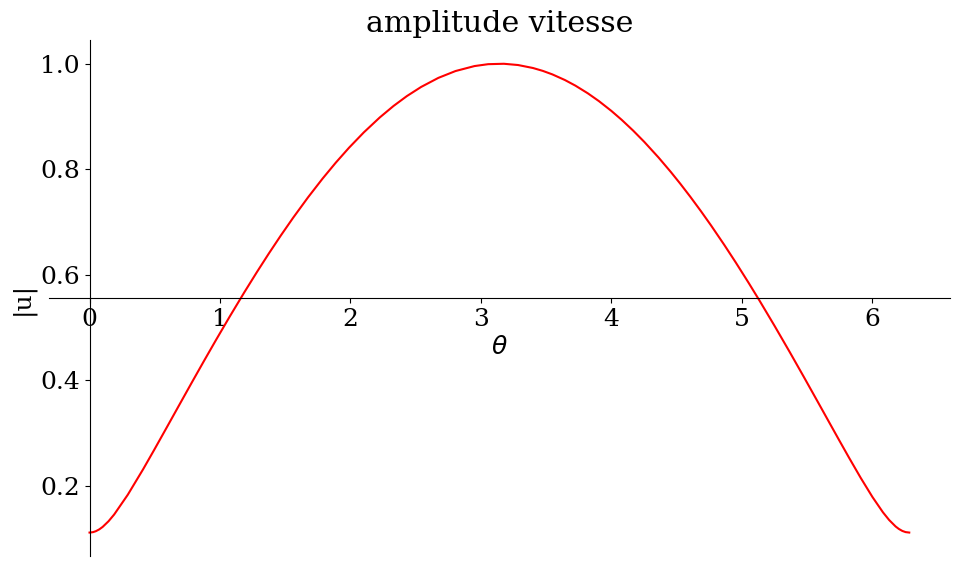
sp.plot(sp.sqrt(dxp**2+dyp**2),(theta,0,tmax),title="amplitude vitesse",ylabel="|u|",
        size=(10,6),line_color='r');

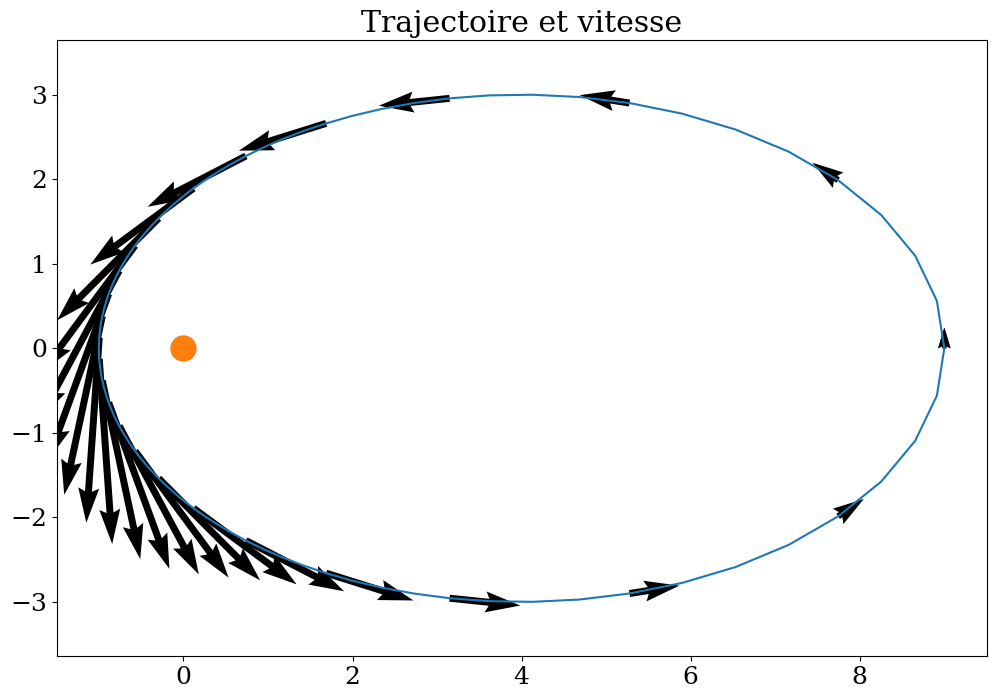
Xm = sp.lambdify(theta,xp)
Ym = sp.lambdify(theta,yp)
Um = sp.lambdify(theta,dxp)
Vm = sp.lambdify(theta,dyp)
plt.figure(figsize=(12,8))
plt.plot(Xm(THETA),Ym(THETA))
plt.quiver(Xm(THETA)[::4],Ym(THETA)[::4],Um(THETA)[::4],Vm(THETA)[::4],scale=5)
plt.plot([0],[0],'o',markersize=18)
plt.title("Trajectoire et vitesse")
plt.axis('equal');

2.4.2. Réponses aux questions ?

1. la vitesse est-elle constante ?

2. le module de la vitesse est-il constant ?

3. si non ou est le minimum ? le maximum ?

4. quelle est la direction de la vitesse ?

2.4.3. Accélération

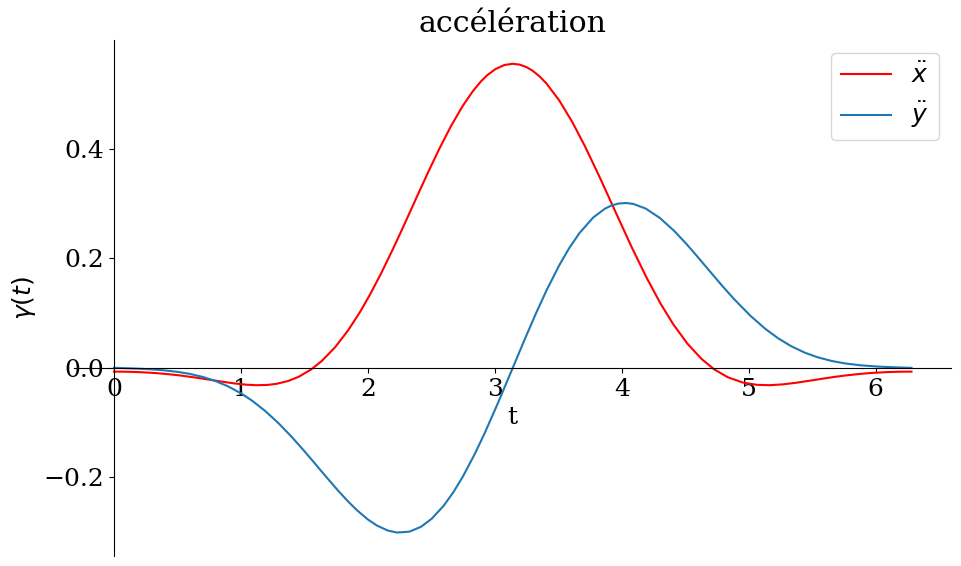
# calcul de l'acceleration
d2xp = dxp.diff(theta)/re**2
d2yp = dyp.diff(theta)/re**2
p1 = sp.plot(d2xp,d2yp,(theta,0,tmax),show=False,size=(10,6),xlabel='t',ylabel='$\gamma(t)$',title="accélération",
            legend=True)
p1[0].line_color='r'
p1[0].label='$\ddot{x}$'
p1[1].label='$\ddot{y}$'
p1.show()

Xm = sp.lambdify(theta,xp)
Ym = sp.lambdify(theta,yp)
Gxm = sp.lambdify(theta,d2xp)
Gym = sp.lambdify(theta,d2yp)
plt.figure(figsize=(12,8))
plt.plot(Xm(THETA),Ym(THETA))
plt.quiver(Xm(THETA)[::4],Ym(THETA)[::4],Gxm(THETA)[::4],Gym(THETA)[::4],scale=5)
plt.plot([0],[0],'o',markersize=18)
plt.title("Trajectoire et accélération")
plt.axis('equal');

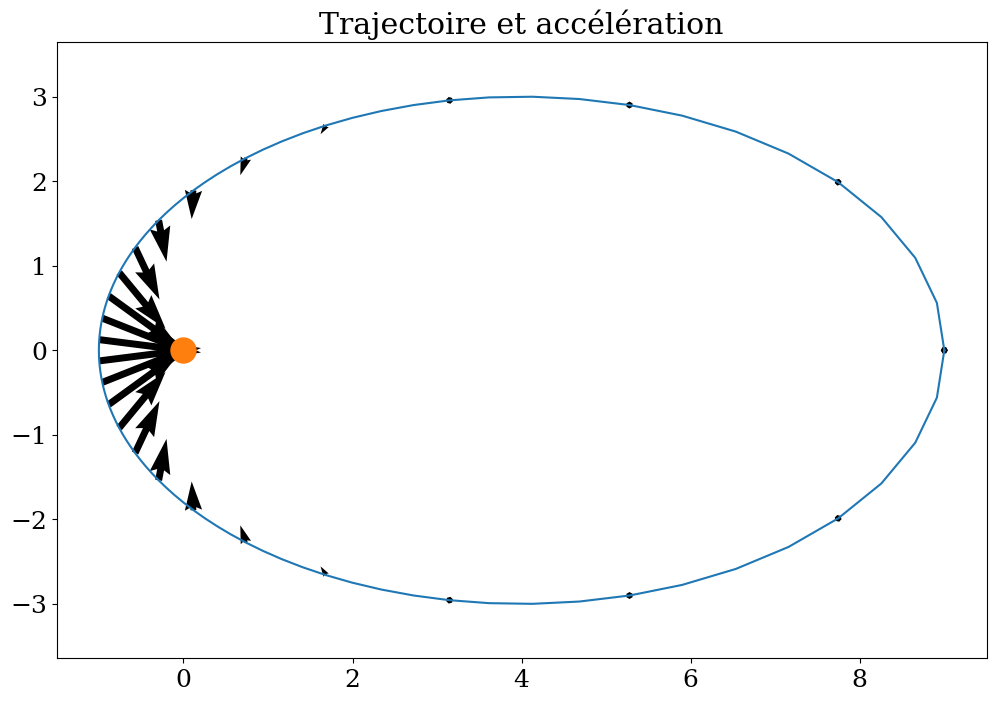
2.4.4. Questions ?

1. l’accélération est-elle constante ?

2. le module de l’accélération est-il constant ?

3. si non ou est le minimum ? le maximum ?

4. quelle est la direction de l’accélération

2.5. Mvt d’un point sur la terre: cinématique en repère mobile

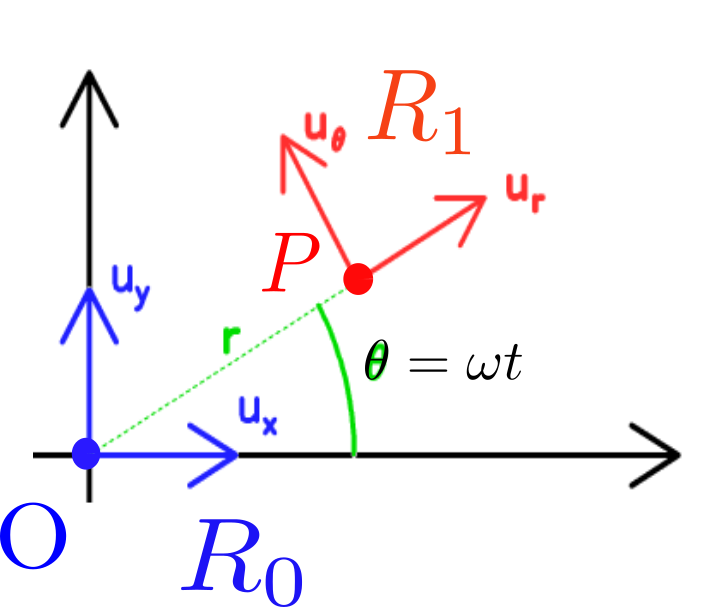
application de la composition des vitesses

1. On note \(\Omega_{R_1/R_0}\) le vecteur de rotation instantané du repère \(R_1\) par rapport à \(R_0\):

on le définit à partir de l’axe instantané de rotation \(\vec{K}\) et de l’angle de rotation \(\omega(t)\) autour de cet axe par:

\[\vec{\Omega}_{R_1/R_0} = \frac{d\omega}{dt} \vec{K}\]

on a alors les propriétés suivantes: $\( \dot{\vec{e}}_{1,x}|_{R_0} = \vec{\Omega}_{R_1/R_0} \wedge \vec{e}_{1,x} \mbox{ , } \dot{\vec{e}}_{1,y}|_{R_0} = \vec{\Omega}_{R_1/R_0} \wedge \vec{e}_{1,y}, \mbox{ .. } \)$

1. Si on connait la vitesse de P dans le repère \(R_1\) et on connaît la vitesse d’un autre point M par rapport à un autre repère \(R_0\),

\[ \vec{V}(P)_{/R_0} = \vec{V}(P)_{/R_1} + \vec{V}(M)_{/R_0} + \vec{\Omega}_{R_1/R_0} \wedge \vec{MP} \]

2. en prenant M=O (point fixe dans \(R_0\))

\[ \vec{V}(P)_{/R_0} = \vec{V}(P)_{/R_1} + \vec{\Omega}_{R_1/R_0} \wedge \vec{OP} \]

2.5.1. Mvt d’un point sur la terre

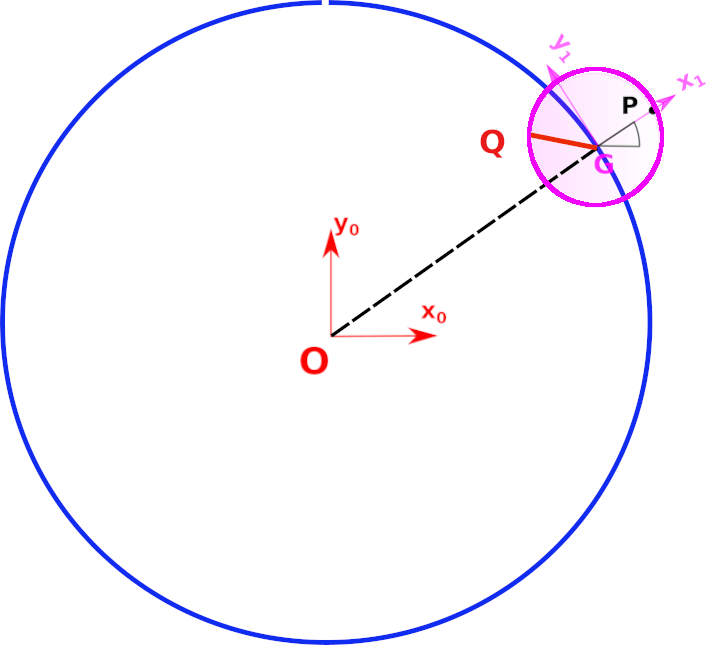
r, omega, R, Omega,  = sp.symbols('r omega R Omega')
R1 = ReferenceFrame("R_1")
R1.orient(R0,'Axis',[Omega*t,R0.z])
display("vitesse angulaire R1/R0=",R1.ang_vel_in(R0))
G = Point('G')
G.set_pos(O,R*R1.x)
G.set_vel(R1,0)
display("Vitesse V(G) / R0 =",G.vel(R0))

'vitesse angulaire R1/R0='

\[\displaystyle \Omega\mathbf{\hat{r_0}_z}\]

'Vitesse V(G) / R0 ='

\[\displaystyle \Omega R\mathbf{\hat{r_1}_y}\]

Q = Point("Q")
Q.set_pos(G,r*sp.cos(omega*t)*R1.x+r*sp.sin(omega*t)*R1.y)
display("Vitesse V(Q)/R1 =",Q.vel(R1))

'Vitesse V(Q)/R1 ='

\[\displaystyle - \omega r \sin{\left(\omega t \right)}\mathbf{\hat{r_1}_x} + \omega r \cos{\left(\omega t \right)}\mathbf{\hat{r_1}_y}\]

# composition des mouvements 
display("composition mvt V(Q)/R0=",Q.vel(R1)+G.vel(R0)+R1.ang_vel_in(R0).cross(Q.pos_from(G)))
display("V(Q)/R0=",Q.vel(R0))

'composition mvt V(Q)/R0='

\[\displaystyle (- \Omega r \sin{\left(\omega t \right)} - \omega r \sin{\left(\omega t \right)})\mathbf{\hat{r_1}_x} + (\Omega R + \Omega r \cos{\left(\omega t \right)} + \omega r \cos{\left(\omega t \right)})\mathbf{\hat{r_1}_y}\]

'V(Q)/R0='

\[\displaystyle (- \Omega r \sin{\left(\omega t \right)} - \omega r \sin{\left(\omega t \right)})\mathbf{\hat{r_1}_x} + (\Omega R + \Omega r \cos{\left(\omega t \right)} + \omega r \cos{\left(\omega t \right)})\mathbf{\hat{r_1}_y}\]

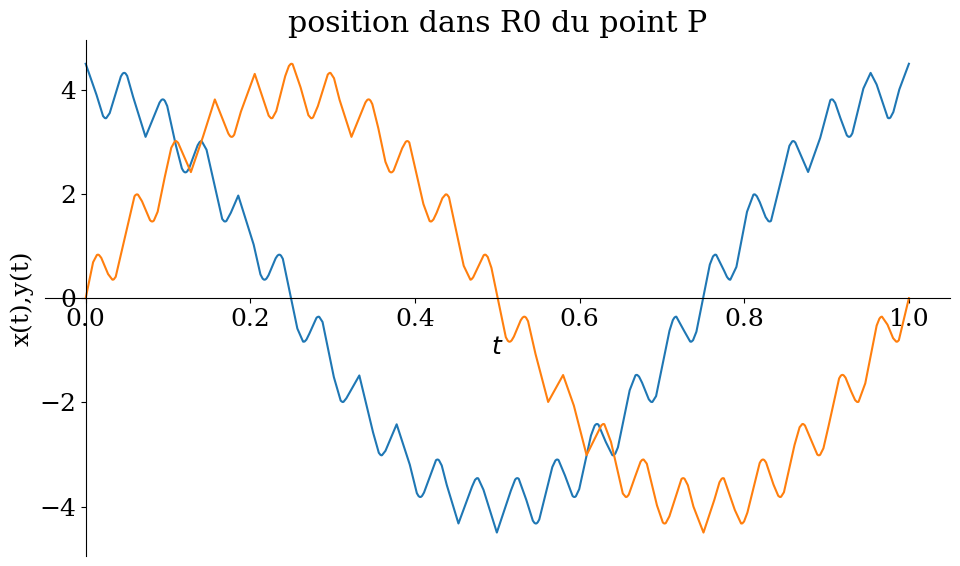
ValNum = {R:4,r:1/sp.S(2),Omega:2*sp.pi, omega:20*2*sp.pi}
tmax = 1

xq = Q.pos_from(O).dot(R0.x).simplify().subs(ValNum)
yq = Q.pos_from(O).dot(R0.y).simplify().subs(ValNum)
sp.plot(xq,yq,(t,0,tmax),size=(10,6),ylabel="x(t),y(t)",title="position dans R0 du point P");

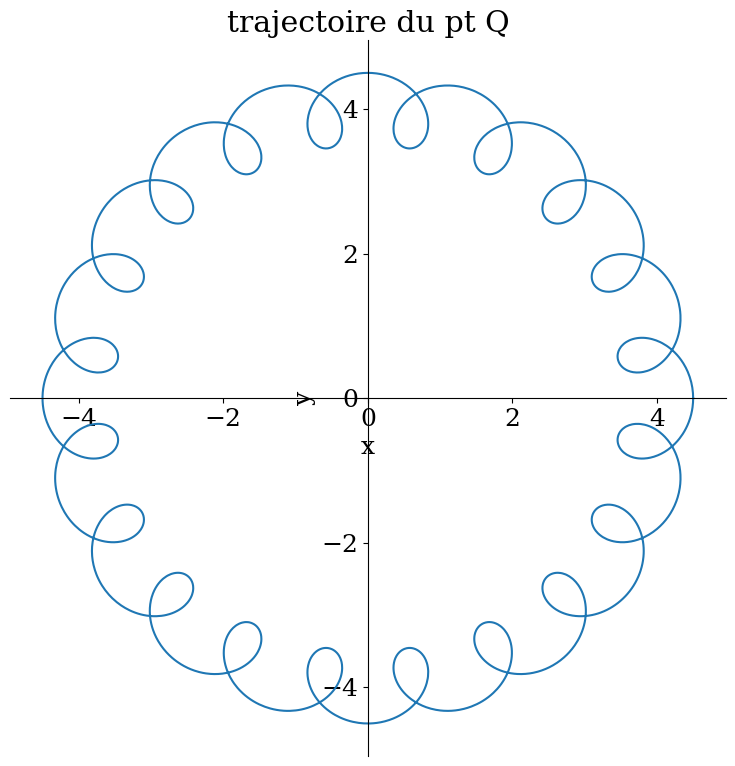
p1 = sp.plot_parametric(xq,yq,(t,0,tmax), size=(10,8), show = False, xlabel='x',ylabel='y',title="trajectoire du pt Q")
p1.aspect_ratio=(1,1)
p1.show()

2.5.2. Vitesse

# calcul de la vitesse
dxq = xq.diff(t)
dyq = yq.diff(t)
display("V=",dxq,dyq)
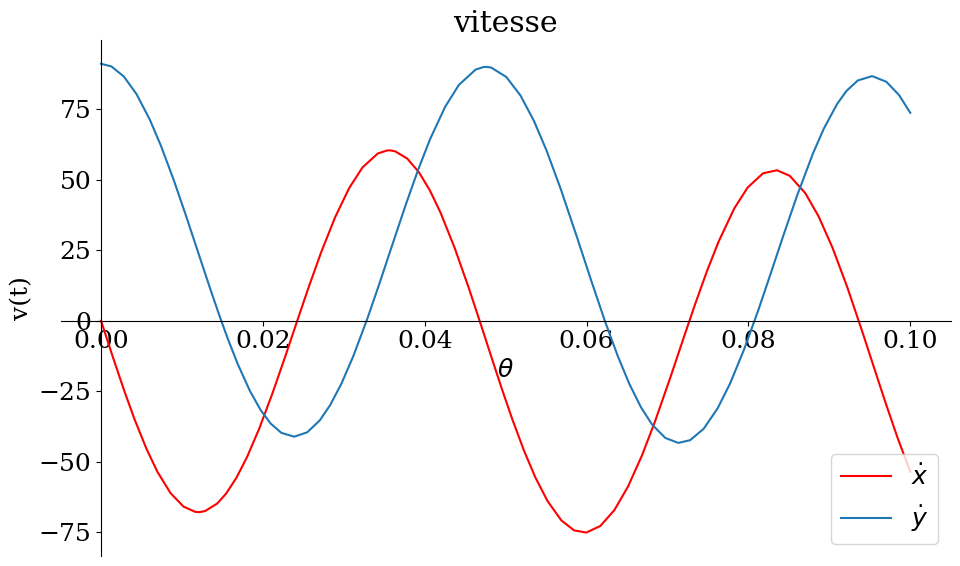
p1 = sp.plot(dxq,dyq,(t,0,tmax/10),show=False,size=(10,6),xlabel='$\\theta$',ylabel='v(t)',title="vitesse",legend=True)
p1[0].line_color='r'
p1[0].label='$\dot{x}$'
p1[1].label='$\dot{y}$'
p1.show()

'V='

\[\displaystyle - 8 \pi \sin{\left(2 \pi t \right)} - 21 \pi \sin{\left(42 \pi t \right)}\]

\[\displaystyle 8 \pi \cos{\left(2 \pi t \right)} + 21 \pi \cos{\left(42 \pi t \right)}\]

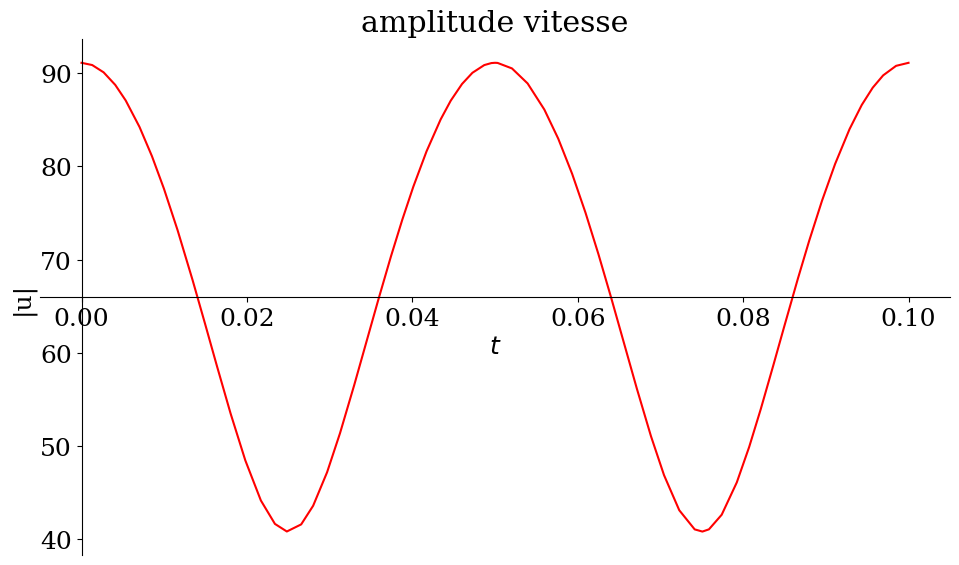
sp.plot(sp.sqrt(dxq**2+dyq**2),(t,0,tmax/10),title="amplitude vitesse",ylabel="|u|",size=(10,6),line_color='r');

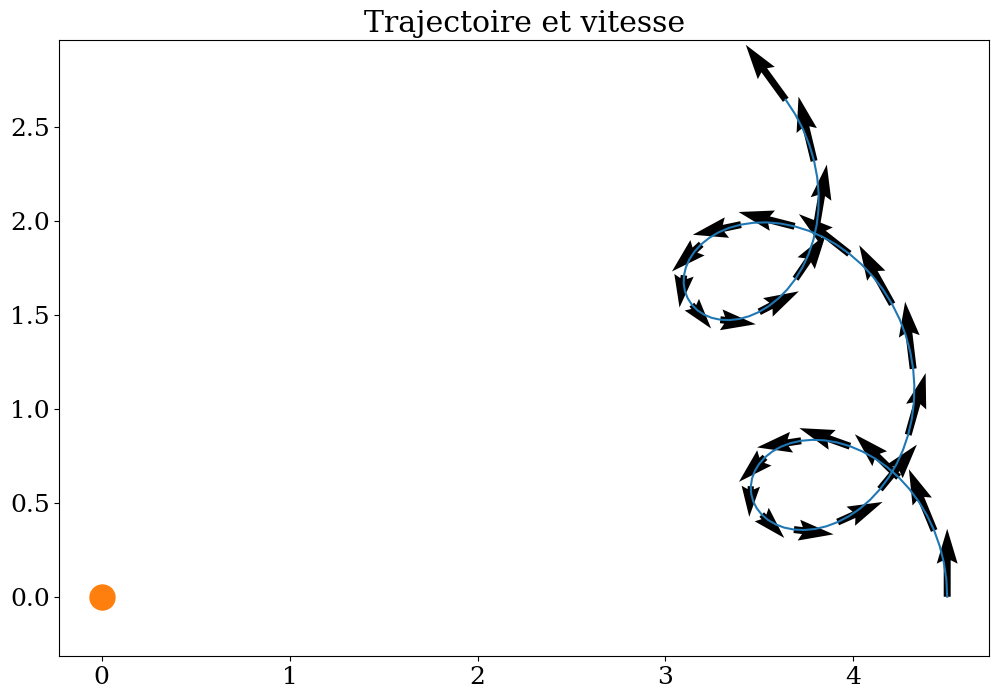
THETA = np.linspace(0,tmax/10,101)
Xm = sp.lambdify(t,xq)
Ym = sp.lambdify(t,yq)
Um = sp.lambdify(t,dxq)
Vm = sp.lambdify(t,dyq)
plt.figure(figsize=(12,8))
plt.plot(Xm(THETA),Ym(THETA))
plt.quiver(Xm(THETA)[::4],Ym(THETA)[::4],Um(THETA)[::4],Vm(THETA)[::4])
plt.plot([0],[0],'o',markersize=18)
plt.title("Trajectoire et vitesse")
plt.axis('equal');

2.5.3. Réponse aux questions ?

1. la vitesse est-elle constante ?

2. le module de la vitesse est-il constant ?

3. si non ou est le minimum ? le maximum ?

4. quelle est la direction de la vitesse ?

2.5.4. Accélération

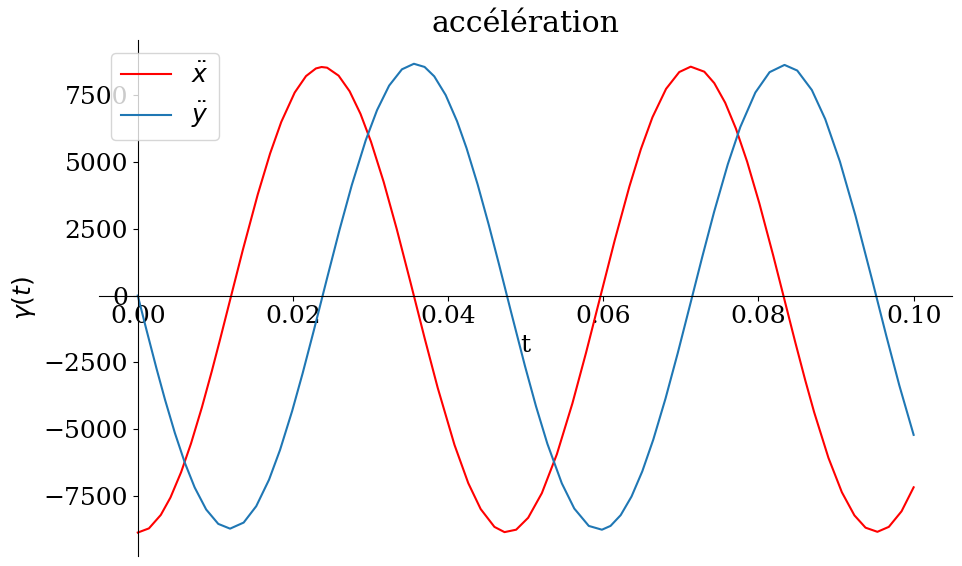
# calcul de l'acceleration
d2xq = dxq.diff(t)
d2yq = dyq.diff(t)
p1 = sp.plot(d2xq,d2yq,(t,0,tmax/10),show=False,size=(10,6),xlabel='t',ylabel='$\gamma(t)$',title="accélération",
            legend=True)
p1[0].line_color='r'
p1[0].label='$\ddot{x}$'
p1[1].label='$\ddot{y}$'
p1.show()

Xm = sp.lambdify(t,xq)
Ym = sp.lambdify(t,yq)
Gxm = sp.lambdify(t,d2xq)
Gym = sp.lambdify(t,d2yq)
plt.figure(figsize=(12,8))
plt.plot(Xm(THETA),Ym(THETA))
plt.quiver(Xm(THETA)[::4],Ym(THETA)[::4],Gxm(THETA)[::4],Gym(THETA)[::4])
plt.title("Trajectoire et accélération")
plt.plot([0],[0],'o',markersize=18)
plt.axis('equal');

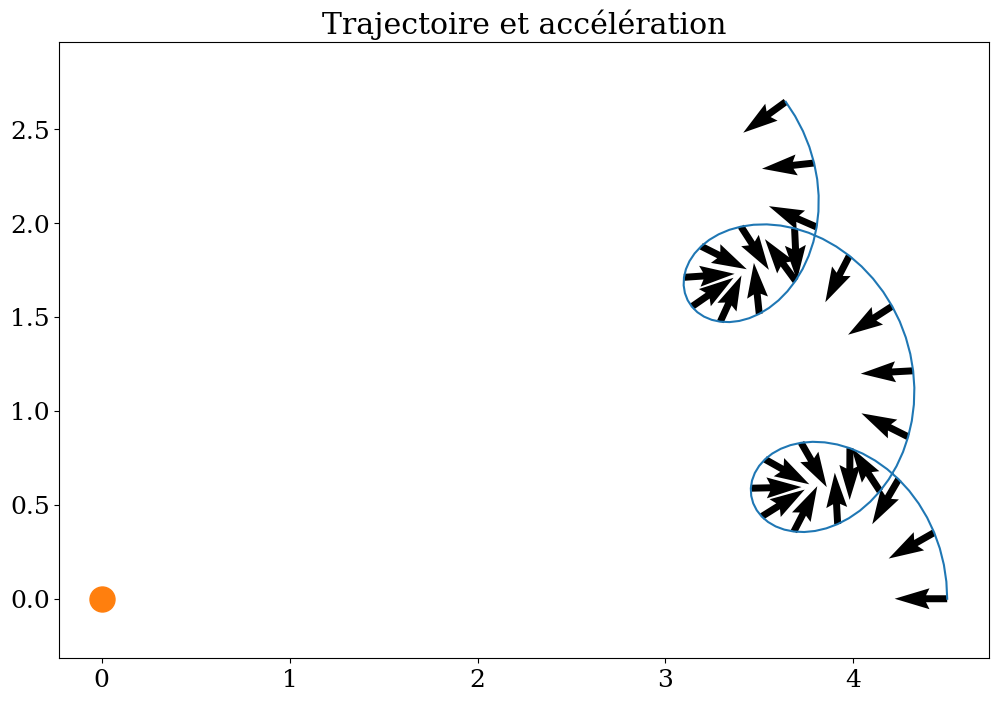
2.5.5. Réponses aux questions ?

1. l’accélération est-elle constante ?

2. le module de l’accélération est-il constant ?

3. si non ou est le minimum ? le maximum ?

4. quelle est la direction de l’accélération

2.6. Calcul numérique de trajectoires en 1D

Les données de la trajectoire sont dans un fichier qui contient le temps (en s.), et la vitesse (en m/s).

Ces données correspondent à la vitesse d’un coureur qui se déplace en ligne droite.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# police des titres
plt.rc('font', family='serif', size='18')
from validation.valide_markdown import test_markdown, test_code
from validation.validation import info_etudiant, bib_validation
from IPython.display import display, Markdown, clear_output
bib_validation('cours','MGC2028L')
from Circuit import Circuit,Circuit2,test_vitesse,test_trajectoire,test_acceleration
Circuit("trajectoire.txt",2.,2.);
T,U,V = np.loadtxt('trajectoire.txt',unpack=True)
T =  T[::10]*2
U = -U[::10]/4.

2.6.1. Trajectoire en 1D

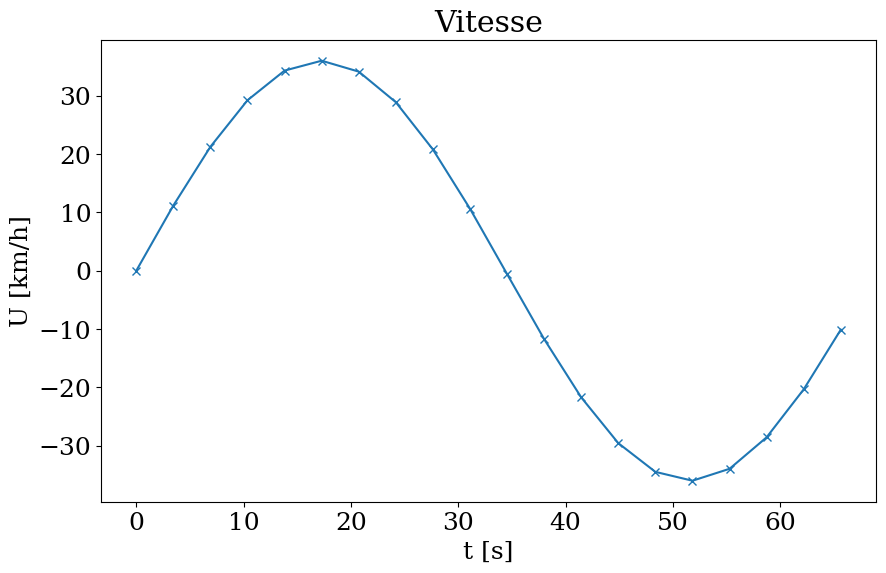
lecture de la vitesse U en fonction du temps

• tracer de la vitesse U en fct de t

plt.figure(figsize=(10,6))
plt.plot(T,U*3.6,'-x')
plt.title("Vitesse")
plt.xlabel('t [s]')
plt.ylabel('U [km/h]');

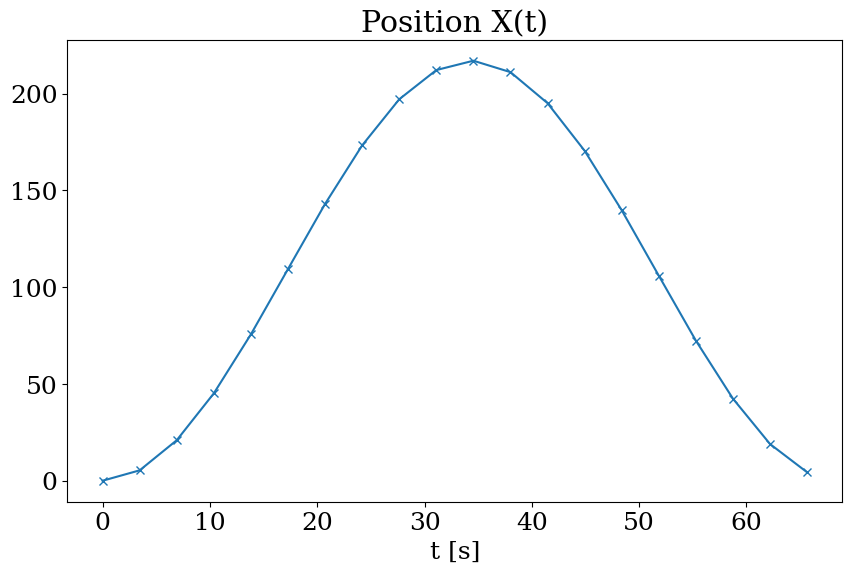
2.6.2. position en fct du temps et distance parcourue

sur l’intervalle de temps \([T_{i-1},T_i]\), la distance parcourue à partir du point \(X_i\) est égale à la vitesse fois le pas en temps \(T{i}-T_{i-1}\):

\[ X_{i} \approx X_{i-1} + \bar{U} dt = X_{i-1} + \frac{(U_{i} + U_{i-1})}{2} (T{i}-T_{i-1}) \]

On trace la courbe X = X(t).

Quelle est alors la trajectoire du coureur?

n = T.size
X = np.zeros(n)
L = 0
for i in range(1,n):
    X[i] = X[i-1] + 0.5*(U[i-1]+U[i])*(T[i]-T[i-1])
    L = L + np.abs(X[i]-X[i-1])
print("distance L en m : ",L)
plt.figure(figsize=(10,6))
plt.plot(T,X,'-x')
plt.title("")
plt.xlabel('t [s]')
plt.title("Position X(t)")

distance L en m :  151.2386474975

Text(0.5, 1.0, 'Position X(t)')

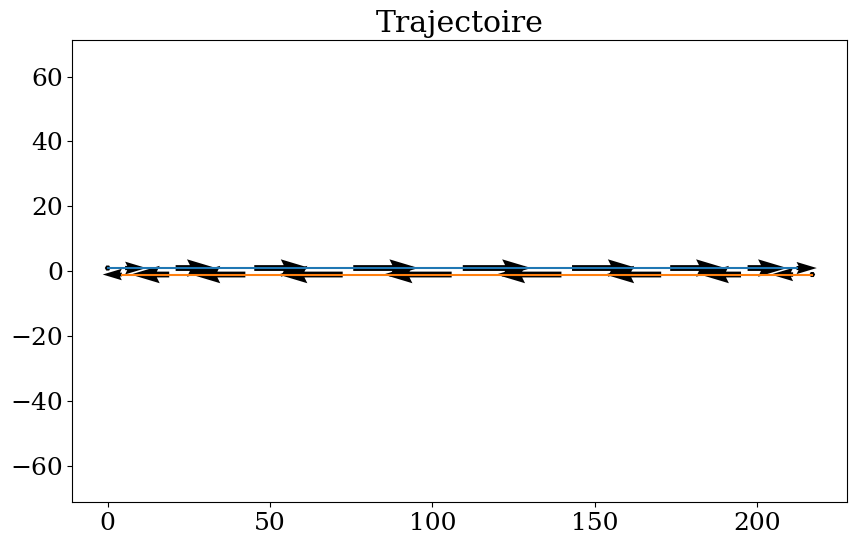
n  = X.size
n2 = n//2
UN = np.ones(n)
plt.figure(figsize=(10,6))
plt.plot(X[:n2], UN[:n2])
plt.quiver(X[:n2], UN[:n2],U[:n2],UN[:n2]*0.) 
plt.plot(X[n2:],-UN[n2:])
plt.quiver(X[n2:],-UN[n2:],U[n2:],UN[n2:]*0.) 
plt.axis('equal')
plt.title("Trajectoire");

2.6.3. Calcul accélération

1. calcul sur chaque segment de temps \([T_{i},T_{i+i}]\)

\[ Gmilieu_i = \frac{\Delta U}{\Delta t} = \frac{U_{i+1} - U_{i}}{T_{i+1} - T_{i}}\]

2. calcul de l’accélération aux points de la trajectoire

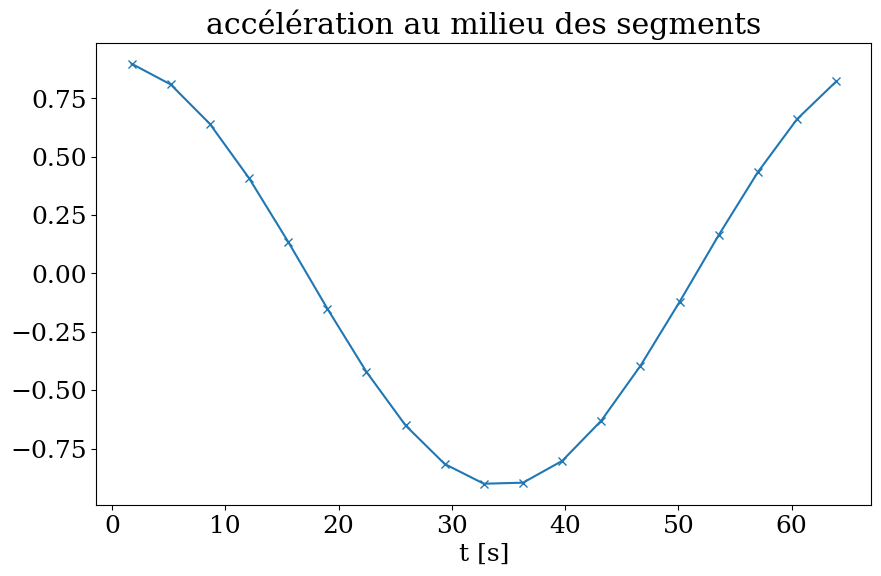
au point \(X_i\) l’accélération \(G_i\) est la moyenne de l’accélération précédente calculée sur le segment \([T_{i-1},T_i]\) et celle calculée sur le segment \([T_{i},T_{i+1}]\)

3. question: a quel moment le coureur accélère et décélère ?

n = T.size
Gmilieu = np.zeros(n-1)
for i in range(n-1):
    Gmilieu[i] = (U[i+1]-U[i])/(T[i+1]-T[i])
plt.figure(figsize=(10,6))
plt.plot(0.5*(T[:-1]+T[1:]),Gmilieu,'-x')
plt.title("accélération au milieu des segments")
plt.xlabel('t [s]')

Text(0.5, 0, 't [s]')

n  = T.size
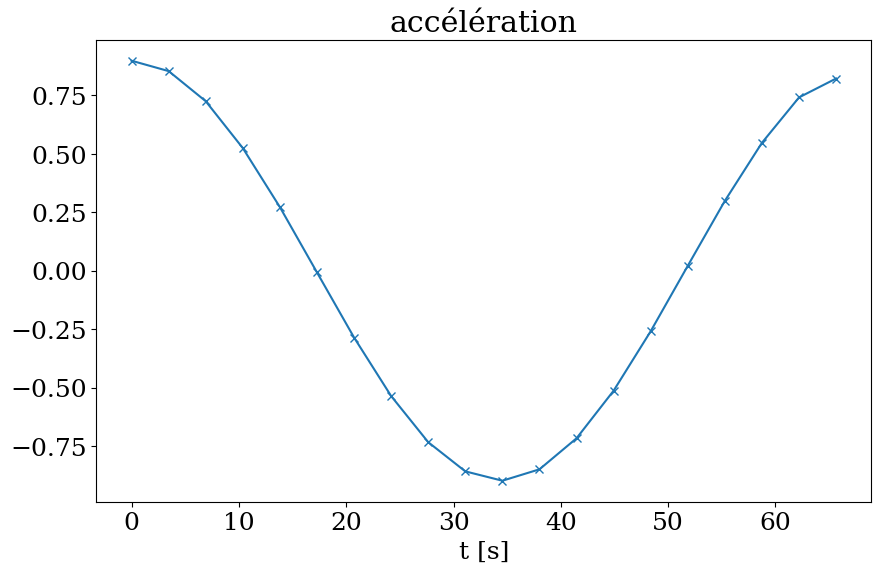
G = np.zeros(n)
G[1:-1] = 0.5 * (Gmilieu[0:-1]+Gmilieu[1:])
# cas particulier
G[0]  = Gmilieu[0]
G[-1] = Gmilieu[-1]
plt.figure(figsize=(10,6))
plt.plot(T,G,'-x')
plt.title("accélération")
plt.xlabel('t [s]')

Text(0.5, 0, 't [s]')

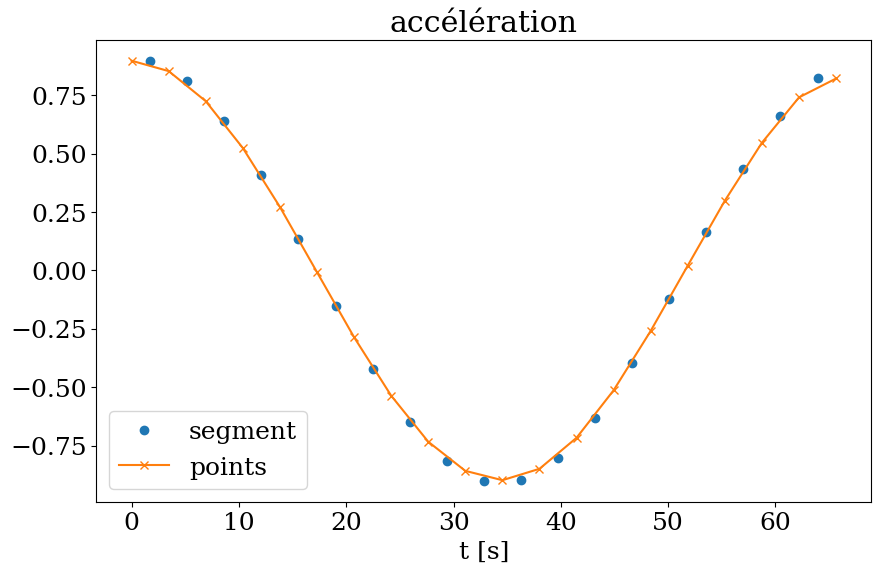
# comparaison
plt.figure(figsize=(10,6))
plt.plot(0.5*(T[:-1]+T[1:]),Gmilieu,'o',label="segment")
plt.plot(T,G,'-x',label="points")
plt.title("accélération")
plt.xlabel('t [s]')
plt.legend();

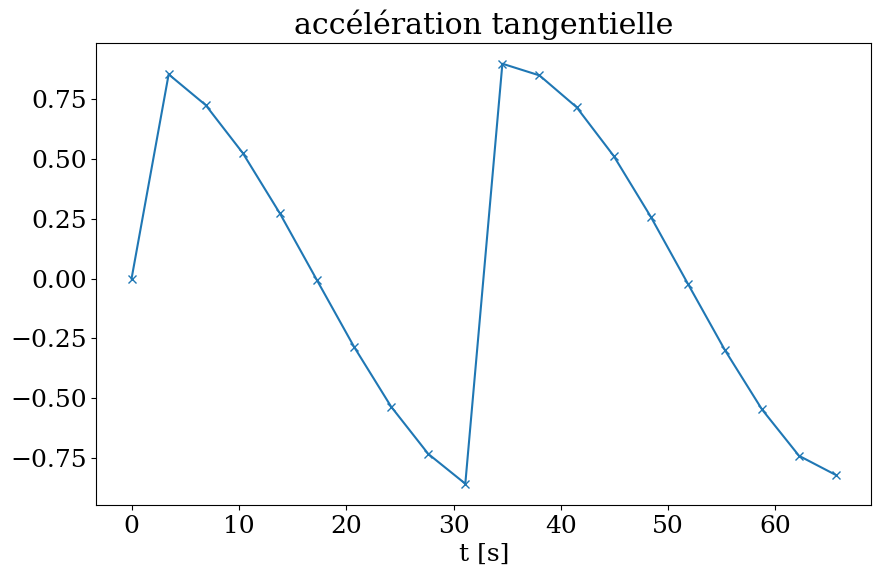
2.6.4. accélération tangentielle

tangente = vecteur unitaire //e à la vitesse

Tn = U / np.abs(U+1.0e-5)
Gn = G*Tn
plt.figure(figsize=(10,6))
plt.plot(T,Gn,'-x')
plt.title("accélération tangentielle")
plt.xlabel('t [s]')

Text(0.5, 0, 't [s]')

2.7. Calcul numérique de trajectoire en 2D

Les données de la trajectoire sont dans le fichier trajectoire.txt qui contient 3 colonnes correspondants au temps (en s.), et aux 2 composantes de la vitesse suivant x et y (en m/s).

2.7.1. lecture des données de vitesse

Dans la cellule suivante:

• lire les données à partir du fichier en utilisant la fonction loadtxt et les mettre dans les 3 tableaux T,U,V

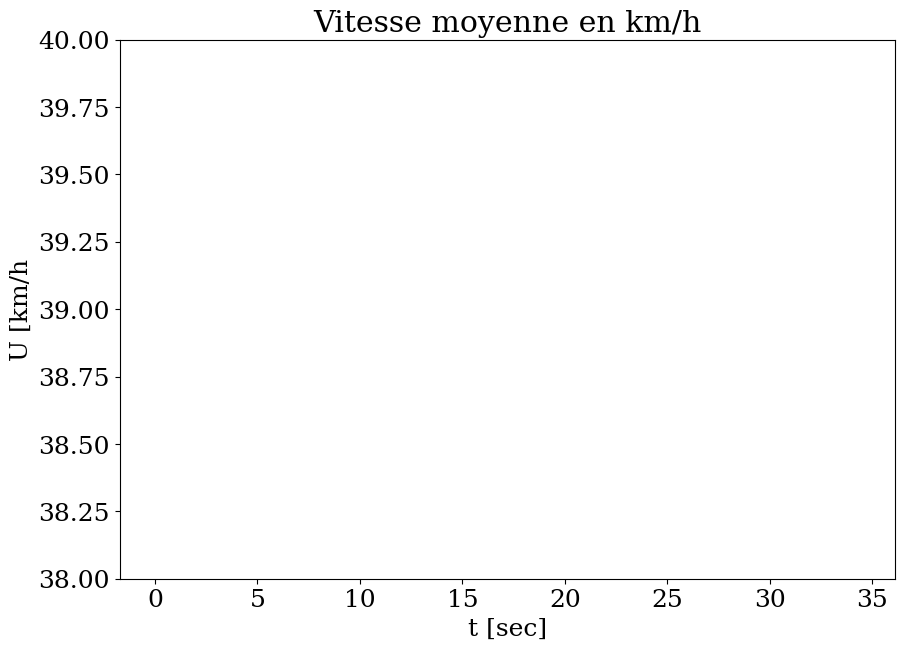
• déterminer l’amplitude de la vitesse moyenne Umean, de la vitesse min Umin et de la vitesse max Umax en km/h

• tracer l’amplitude de la vitesse en fonction du temps et sauvegarder la courbe dans un fichier, que vous devez -inclure ensuite dans votre contre rendu.

On pourra utiliser la fonction matplotlib plt.ylim([ymin,ymax]) pour définir les valeurs min et max de l’axe y (ymin et ymax sont des valeurs numériques à choisir)

T = None
U = None
V = None
Umean = None
Vmin  = None
Umax  = None
### BEGIN SOLUTION
T,U,V = np.loadtxt('trajectoire.txt',unpack=True)
Um = np.sqrt(U**2 + V**2)*3.600
Umean = Um.mean()
Umax = Um.max()
Umin = Um.min()
print("Vitesse moyenne={:.1f}km/h min={:.1f} km/h max={:.1f}km/h".format(Umean,Umin,Umax))
plt.figure(figsize=(10,7))
plt.plot(T,Um)
plt.xlabel('t [sec]')
plt.ylabel('U [km/h')
plt.ylim([38,40])
plt.title("Vitesse moyenne en km/h");
#plt.savefig("vitesse.png")
### END SOLUTION

Vitesse moyenne=43.0km/h min=43.0 km/h max=43.0km/h

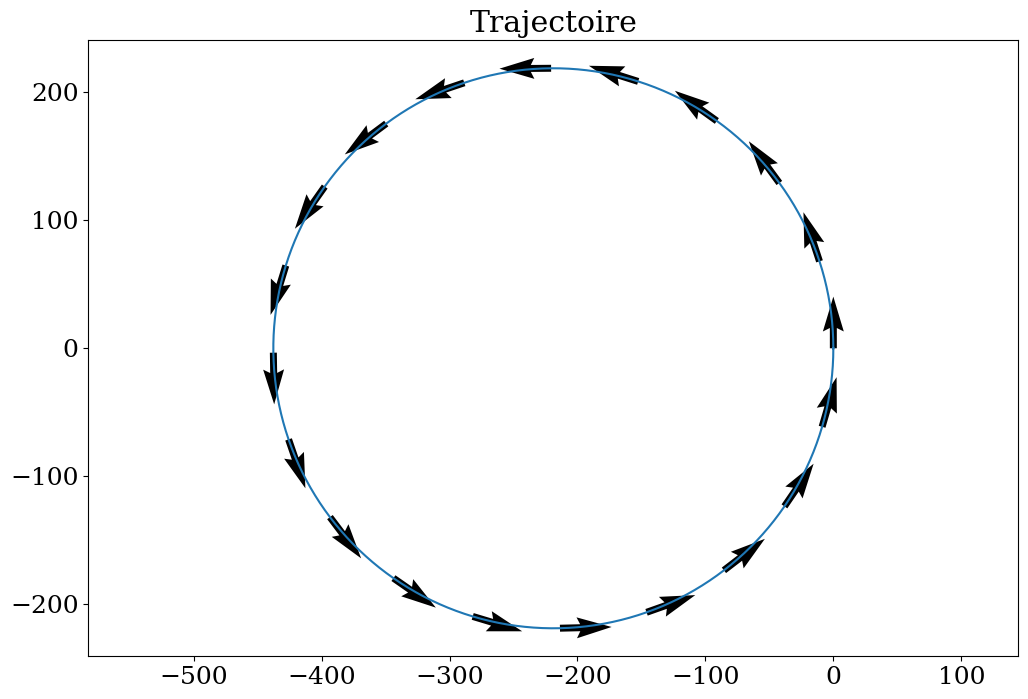
2.7.2. Calcul de la trajectoire

A partir des composantes de vitesse U et V , calculer la trajectoire en fonction du temps, i.e. la position \(X_i\) et \(Y_i\) pour chacun des temps \(T_i\). Sur chaque intervalle \([T_{i-1},T_i]\), on utilisera la vitesse moyenne pour calculer la position à l’instant \(T_i\) en fonction de la position précédente \(T_{i-1}\), i.e.

\[ X_{i} \approx X_{i-1} + \bar{U} dt = X_{i-1} + \frac{(U_{i} + U_{i-1})}{2} (T{i}-T_{i-1}) \]

Dans la cellule suivante:

1. calcul la position des points de la trajectoire dans les 2 vecteurs numpy X et Y

2. en déduire la longueur de la trajectoire dans la variable L

3. vérifier le calcul par comparaison avec la vitesse moyenne précédente

4. tracer la trajectoire (X,Y) ainsi que la vitesse sur le même graphe et sauvegarder la courbe dans un fichier, que vous devez inclure ensuite dans votre contre rendu.

On utilisera la fonction plt.quiver(X,Y,U,V) qui permet de tracer des flèches de longueur U,V aux points X,Y. Pour éviter de tracer trop de flèches, on pourra prendre un point sur 4 en remplaçant X par X[::4] et idem pour les autres arguments.

N = T.size
X = np.zeros(N)
Y = np.zeros(N)
for i in range(1,N):
    X[i] = X[i-1] + 0.5*(U[i]+U[i-1])*(T[i]-T[i-1])
    Y[i] = Y[i-1] + 0.5*(V[i]+V[i-1])*(T[i]-T[i-1])
# calcul longueur
L = 0
for i in range(1,X.size):
    L += np.sqrt((X[i]-X[i-1])**2 + (Y[i]-Y[i-1])**2)
# tracer
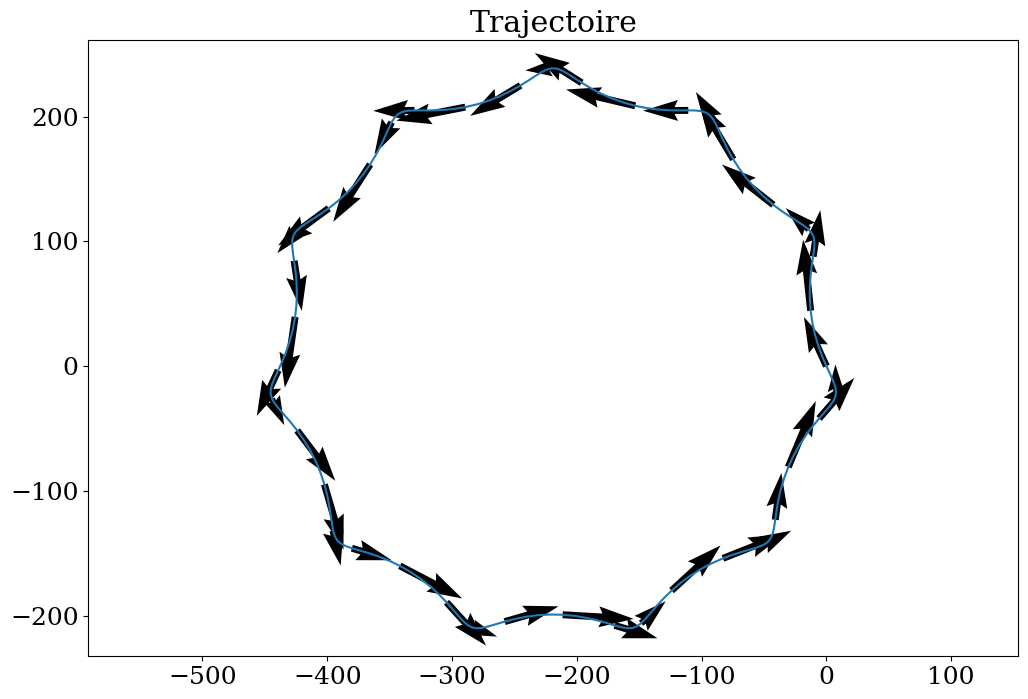
plt.figure(figsize=(12,8))
plt.plot(X,Y)
plt.quiver(X[::10],Y[::10],U[::10],V[::10])
plt.title("Trajectoire")
plt.axis('equal');
#plt.savefig("trajectoire.png")

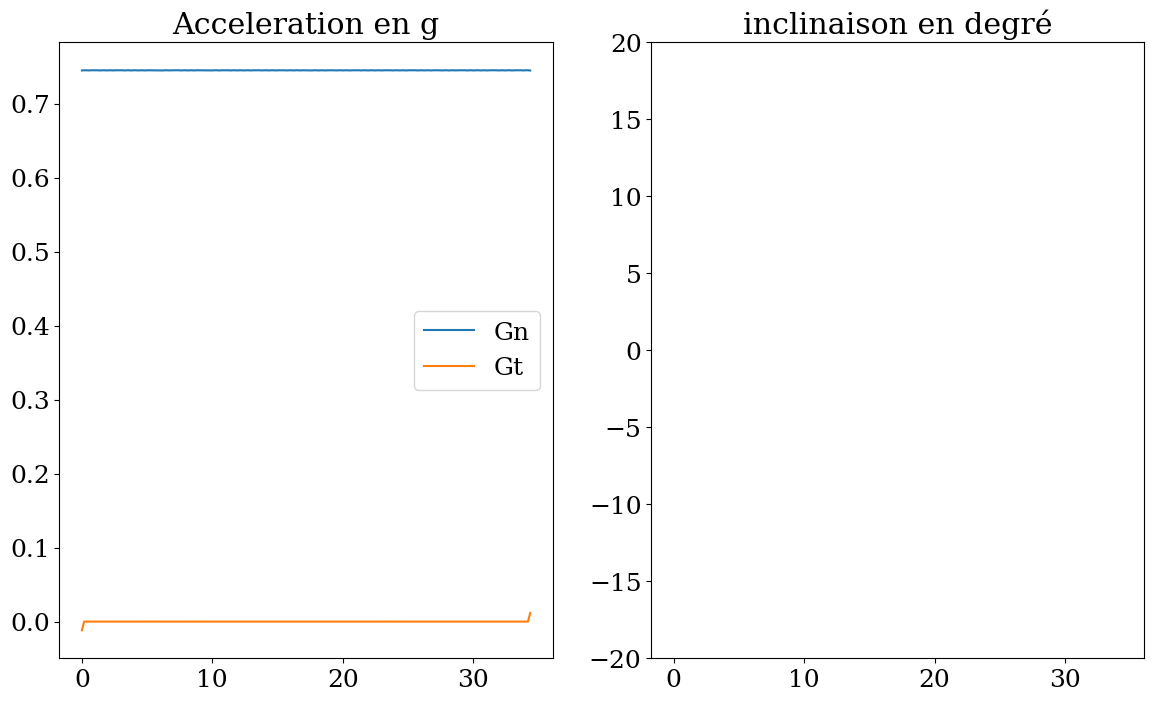
2.7.3. Calcul de l’accélération

On veut calculer l’angle \(\theta\) d’inclinaison du cycliste, qui correspond à l’équilibre des forces dans le référentiel lié au cycliste dans le plan de la figure:

\[ \vec{F_c} + \vec{P} + \vec{R} = \vec{0}\]

La force centrifuge \(\vec{F_c} = - M \vec{\gamma_n}\) est une force fictive qui est opposée à l’accélération dans la direction normale, et qui traduit cet équilibre statique dans le référentiel lié au cycliste. Dans le référentiel fixe, on retrouve le PFD dans le plan de la figure:

\[ \vec{F_c} + \vec{P} = M \vec{\gamma_n}\]

Remarque dans la direction tangentielle (i.e. la direction perpendiculaire au plan de la figure) on a un équilibre entre l’accélération tangentielle, la force de traction, et les forces de frottements.

Pour calculer \(\theta\), il faut donc calculer l’accélération tangentielle et normale, i.e. le vecteur accélération projeté dans le référentiel local directe formé par la tangente et la normale en chaque point de la trajectoire.

Dans la cellule suivante, on va :

1. Calculer les composantes suivant x et y de l’accélération au milieu de chacun des segments \([T_{i},T_{i+1}]\) de la trajectoire, en utilisant l’accroissement de vitesse suivant x et suivant y. On mettra le résultat dans les vecteurs numpy Gmilieux et Gmilieuy respectivement. L’accélération suivant x sur le ième segment \([T_{i},T_{i+1}]\) s’écrit:

\[ Gmilieux_i = \frac{\Delta U}{\Delta t} = \frac{U_{i+1} - U_{i}}{T_{i+1} - T_{i}}\]

2. Calculer les composantes suivant x et y de l’accélération en chacun des points de la trajectoire correspondant à chaque instant \(T_i\) en moyennant chaque accélération Gmilieux et Gmilieuy. On mettra le résultat dans Gx et Gy. Attention au cas particulier du premier et du dernier point de la trajectoire !

3. Calculer en chacun des points de la trajectoire les composantes suivant x et y de la tangente (vecteur unitaire) dans les vecteurs numpy Tx et Ty. En déduire les composantes de la normale (vecteur unitaire) dans Ǹx et Ǹy tel que le repétre (\(\vec{t},\vect{n},\vect{e_z}\)) soit orthonormé direct.

4. Calculer par projection la composante de l’accélération tangentielle et celle de l’accélération normale à chaque instant \(T_i\). On mettra le résultat dans les vecteurs Gt et Gn.

5. En déduire l’angle d’inclinaison \(\theta\) en degré du cycliste pour composer la force centrifuge en prenant \(g=9.81\). On mettra le résultat dans le tableau numpy THETA. On pourra utiliser la fonction numpy arctan2(a,b) qui calcule l’angle en radian dont la tangente vaut \(a/b\).

N = X.size
Gmilieux = np.zeros(N-1)
Gmilieuy = np.zeros(N-1)
for i in range(0,N-1):
    Gmilieux[i] = (U[i+1]-U[i])/(T[i+1]-T[i])
    Gmilieuy[i] = (V[i+1]-V[i])/(T[i+1]-T[i])
Gx = np.zeros(N)
Gy = np.zeros(N)
Gx[1:-1] = 0.5*(Gmilieux[:-1]+Gmilieux[1:])
Gx[0]  = Gmilieux[0]
Gx[-1] = Gmilieux[-1]
Gy[1:-1] = 0.5*(Gmilieuy[:-1]+Gmilieuy[1:])
Gy[0]  = Gmilieuy[0]
Gy[-1] = Gmilieuy[-1]
#
Un = np.sqrt(U**2 + V**2)
Tx = U/Un
Ty = V/Un 
Nx = -Ty
Ny =  Tx
#
Gt = Gx*Tx + Gy*Ty
Gn = Gx*Nx + Gy*Ny
# calcul de l'angle
g = 9.81
THETA = np.rad2deg(np.arctan2(Gn,g))
# tracer
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(T,Gn/g,label="Gn")
plt.plot(T,Gt/g,label='Gt')
plt.legend()
plt.title("Acceleration en g");
plt.subplot(1,2,2)
plt.plot(T,THETA)
plt.ylim(-20,20)
plt.title("inclinaison en degré");

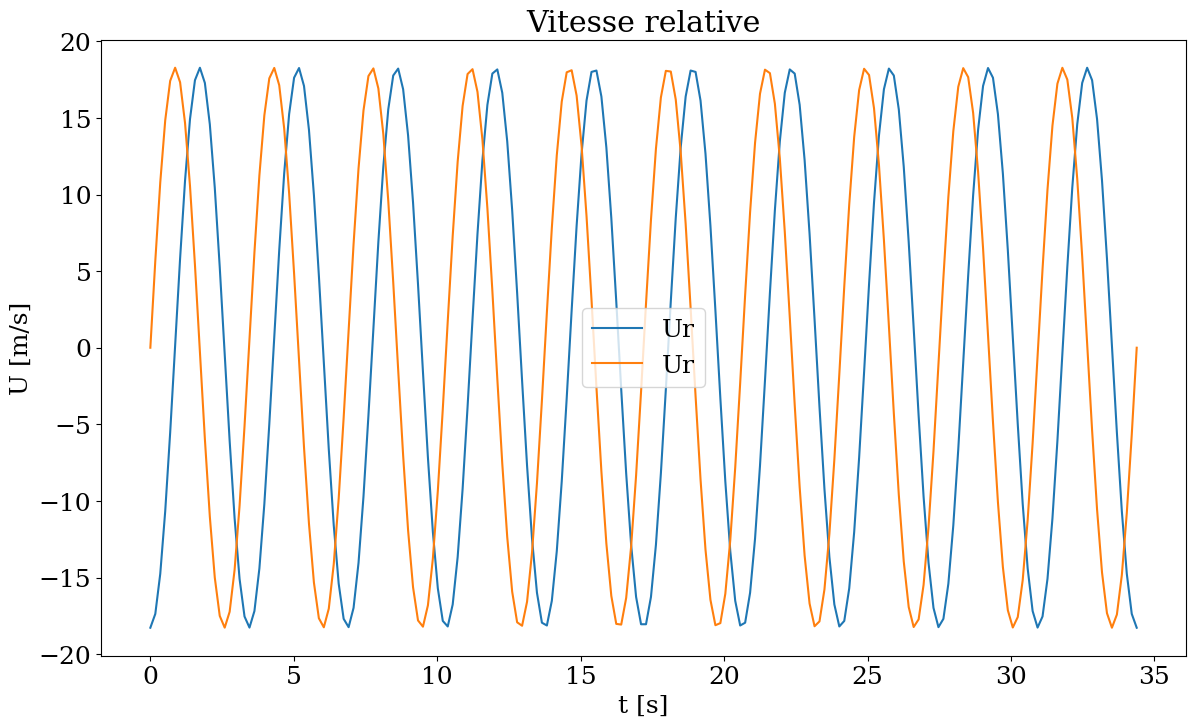
2.8. Mouvement d’un disque en rotation

On veut maintenant étudier le mouvement d’un point d’un disque en rotation uniforme et dont l’axe de rotation décrit le circuit précédent avec la même vitesse que le cycliste.

Le disque a un rayon \(R\) de 10m. La période de rotation du disque est égale à 1/p du temps de parcours de la trajectoire.

Dans la cellule suivante, calculer la vitesse relative d’un point du disque à chaque instant t dans le tableau T2, projetée dans le référentiel fixe, et on écrira le résultat dans les tableaux Ur et Vr.

Tracer l’évolution de cette vitesse en fonction du temps.

R = 10
Ur = 0
Vr = 0
p  = 10
#p  = 8
#p  = 5
#p  = 2
## BEGIN SOLUTION
omega = 2*np.pi*p/(T[-1]-T[0])
Ur = -omega*R*np.cos(omega*T)
Vr =  omega*R*np.sin(omega*T)
plt.figure(figsize=(14,8))
plt.plot(T,Ur,label="Ur")
plt.plot(T,Vr,label="Ur")
plt.legend()
plt.xlabel('t [s]')
plt.ylabel('U [m/s]')
plt.title("Vitesse relative")
## END SOLUTION

Text(0.5, 1.0, 'Vitesse relative')

2.8.1. Composition de mouvement

En utilisant la composition du mouvement, calculer la vitesse absolue de ce point du disque projetée dans le référentiel fixe. Le résultat sera écrit dans les tableaux Ud et Vd.

• calculer la vitesse moyenne Udmean

• calcul la valeur min et max dans Udmin et Udmax

Ud = 0
Vd = 0
Udmean = None
Udmin  = None
Udmax  = None
### BEGIN SOLUTION
Ud = U + Ur
Vd = V + Vr
Udm = np.sqrt(Ud**2 + Vd**2)*3.600
Udmean = Udm.mean()
Udmax = Udm.max()
Udmin = Udm.min()
plt.figure(figsize=(10,7))
plt.plot(T,Udm)
plt.xlabel('t [sec]')
plt.ylabel('U [km/h]')
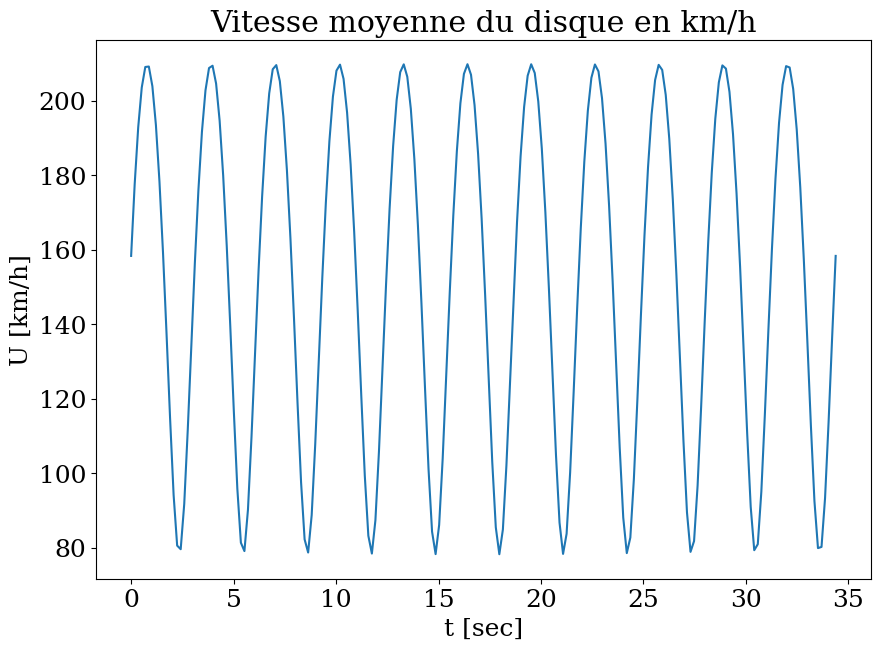
plt.title("Vitesse moyenne du disque en km/h");
#plt.savefig("vitessed.png")
### END SOLUTION

2.8.2. Calcul de la trajectoire

A partir des composantes de vitesse Ud et d2 , calculer la trajectoire en fonction du temps, i.e. la position \(Xd_i\) et \(Yd_i\) pour chacun des temps \(T2_i\). Sur chaque intervalle \([T2_{i-1},T2_i]\), on utilisera la vitesse moyenne pour calculer la position à l’instant \(T2_i\) en fonction de la position précédente \(T2_{i-1}\).

Dans la cellule suivante:

1. calcul la position des points de la trajectoire dans les 2 vecteurs numpy Xd et Yd

2. en déduire la longueur de la trajectoire dans la variable Ld

3. vérifier le calcul par comparaison avec la vitesse moyenne précédente

4. tracer la trajectoire (Xd,Yd) ainsi que la vitesse et sauvegarder la courbe dans un fichier, que vous devez inclure ensuite dans votre contre rendu.

5. Expliquer en quelques lignes dans le compte rendu comment vous avez vérifié votre calcul

Xd = None
Yd = None
Ld = None
### BEGIN SOLUTION
N = T.size
Xd = np.zeros(N)
Yd = np.zeros(N)
for i in range(1,N):
    Xd[i] = Xd[i-1] + 0.5*(Ud[i]+Ud[i-1])*(T[i]-T[i-1])
    Yd[i] = Yd[i-1] + 0.5*(Vd[i]+Vd[i-1])*(T[i]-T[i-1])
# calcul longueur
Ld = 0
for i in range(1,Xd.size):
    Ld += np.sqrt((Xd[i]-Xd[i-1])**2 + (Yd[i]-Yd[i-1])**2)
# tracer
plt.figure(figsize=(12,8))
plt.plot(Xd,Yd)
plt.quiver(Xd[::5],Yd[::5],Ud[::5],Vd[::5])
plt.title("Trajectoire")
plt.axis('equal');
# plt.savefig("vitesse2.png")
### END SOLUTION

2.9. FIN de la leçon