Mouvement d’une perle sur un cerceau

Contenu

10. Mouvement d’une perle sur un cerceau#

Marc Buffat département mécanique Lyon 1

10.1. Objectif#

On souhaite étudier le mouvement d’une bille sur un cerceau qui tourne avec une vitesse constante $\omega$ autour de $Oz$

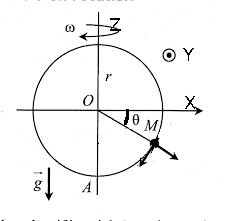
bille

Le cerceau a un rayon $R$ et on considère que la bille a une masse $M$ à la position B sur ce cerceau avec un angle $\theta$ et glisse sans frottement. A l’instant initiale la bille est lachée à une position initiale $\theta = \theta_0$ avec $\dot{\theta}=0$

L’objectif est de déterminer la position de la bille en utilisant le formalisme du cours. Dans une première partie, on reprend le formalisme du cours pour obtenir les équations du mouvement. Ensuite chaque étudiant aura des valeurs particulières à traiter pour résoudre numériquement le système.

Le travail demandé est l’analyse des résultats de la simulation avec une visualisation du mouvement de la bille.

Un compte rendu synthétique est attendu pour chaque étudiants à la fin du notebook.

%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
# bibliotheque mecanique
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum
from sympy.physics.vector import time_derivative,dot
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
# simulation
from validation.validation import info_etudiant, bib_validation
from validation.valide_markdown import test_markdown, test_code
bib_validation('cours','MGC2014L')
import k3d
from Bille import Bille
from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
    #raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_    = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Etudiant {} {}  id={}**".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_R = np.round(0.1+1*np.random.rand(),2)
_M = np.round(0.1+1*np.random.rand(),2)
_g = 9.81
_omega = np.round(np.sqrt(2*_g/_R),2)
printmd("Paramétres de l'étude: R={} M={} omega={} g={}".format(_R,_M,_omega,_g))

---------------------------------------------------------------------------
ModuleNotFoundError                       Traceback (most recent call last)
Cell In[1], line 17
     15 bib_validation('cours','MGC2014L')
     16 import k3d
---> 17 from Bille import Bille
     18 from IPython.display import display, Markdown, clear_output
     19 def printmd(string):

ModuleNotFoundError: No module named 'Bille'

10.2. Modèle Mécanique#

On définit:

les paramètres du problème, soit le rayon $R$ du cerceau, la masse M de la bille, et la vitesse de rotation $\omega$ du cerceau
le degrés de liberté de a bille: l’angle $\theta$
les repères et les points
- le repère fixe $R_0$ , associé au centre fixe $O$ du cerceau
- le repère $R_1$ lié au cerceau, en rotation de vitesse $\omega$ autour de $R_0.z$
- le repère $R_2$ lié à la bille et la position $B$ de la bille

10.2.1. paramètres du problème#

# parametres du problème: rayon masse du cerceau position masse 
R, M, g, omega = sp.symbols('R M g omega')
t = sp.symbols('t')
# degrés de liberté
theta  = dynamicsymbols('theta')

10.2.2. repère et position des points#

# reperes et points
O = Point('O')
R0 = ReferenceFrame('R_0')
# cerceau
R1 = ReferenceFrame('R_1')
R1.orient(R0,'Axis',[omega*t, R0.z])
# bille 
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[theta, R1.y])
# position bille B
B = Point('B')
B.set_pos(O,R*R2.x)

10.2.3. Calcul de la quantité de mouvement de la bille#

10.2.3.1. calcul de la vitesse de B#

En appliquant la composition des mouvements à la bille, calculer sa vitesse dans $R_0$.

On rappelle que connaissant la vitesse d’un point P dans un repère R1, on peut calculer sa vitesse dans R0 par composition des vitesses avec à un autre point A

\[\underbrace{\overrightarrow{V}^{\,R_0}_P}_\textrm{V absolue} = \underbrace{\overrightarrow{V}^{\,R_1}_P}_\textrm{V relative} + \underbrace{\overrightarrow{V}^{\,R_0}_A + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{AP}}_\textrm{V entraînement}\]

on peut alors utiliser la méthode P.v1pt_theory(A,R0,R1) ou 1 point theory (les 2 points n’appartiennent pas au même solide)

Questions:

définir la vitesse de O dans R0 et B dans R2 avec set_vel(frame,valeur)
utiliser la composition des vitesses pour calculer la vitesse de B dans $R_0$

# definition et calcul des vitesses de O et B dans R0

## BEGIN SOLUTION
O.set_vel(R0,0.)
B.set_vel(R2,0.)
B.v1pt_theory(O,R0,R2)
B.vel(R0)
## END SOLUTION

display("V(B) / R0=",B.vel(R0))
assert(B.vel(R0) != 0 and B.vel(R0).dot(R2.x) == 0)

10.2.3.2. quantité de mouvement#

On définit la bille comme une masse ponctuelle en utilisant la méthode Particle en définissant simplement sa position et sa masse. Sa quantité de mouvement est alors obtenue par la méthode linear_momentum(frame)

On définit aussi son energie potentielle : $M g z_B$

bille   = Particle('bille',B,M)
# quantite de mouvement de la bille
display("QB=",bille.linear_momentum(R0))
# energie potentiel
bille.potential_energy =  M*g*B.pos_from(O).dot(R0.z)
display("Ep=",bille.potential_energy )

10.2.4. PFD pour la bille en B#

On applique le PFD à la bille:

variation de la quantité de mouvement = somme des forces appliquées

soit $$\frac{d}{dt}(M \vec{V_B})|R_0 = \sum \vec{forces} $$

Les forces appliquées sur la bille sont:

la réaction du cerceau sur la bille $\vec{R_b}$ (sans composante suivant R2.z car sans frottement) que l’on écrit dans $R_2$:

\[ \vec{R_b} = R_bx \vec{R_2.x} + R_by \vec{R_2.y}\]

le poids $\vec{P}$ suivant $R_0.z$

On calcul la variation de la quantité de mouvement par dérivation temporelle par rapport à $R_0$ avec la fonction time_derivative(vecteur, frame)

En introduisant les 2 composantes $Rb_x $, $Rb_y$ de $\vec{R_b}$ comme paramètres, calculer les forces appliquées dans P et RB

# parametres
Rbx,Rby = sp.symbols('Rb_x Rb_y ')
# dérivée de la quantité de mouvement
QB = time_derivative(bille.linear_momentum(R0),R0)
# force 
P = 0
RB = 0
## BEGIN SOLUTION
P = -M*g*R0.z
RB = Rbx*R2.x + Rby*R2.y
## END SOLUTION

display("QB=",QB)
display("P=",P,"Rb=",RB)
assert(P.dot(R0.z) != 0)
assert(RB.dot(R2.z) == 0)

10.2.4.1. équations du mouvement#

en projetant le PFD sur les 3 axes du repère $R_2$, écrire les 3 équations du mouvement dans les 3 variables eq1 eq2 eq3. Les 3 equations sont écrite sous la forme $$ eq_1 = 0 \;,\; eq_2 = 0 \;,\; eq_3 = 0$$ et on met dans chacune des variables le membre de gauche.

On utilisera la méthode .dot(vecteur) pour calculer le produit scalaire d’une expression vectorielle avec un vecteur.

# equations du mouvement
eq1 = 0
eq2 = 0
eq3 = 0
## BEGIN SOLUTION
FB = P + RB
eq1=(QB-FB).dot(R2.x)
eq2=(QB-FB).dot(R2.y)
eq3=(QB-FB).dot(R2.z)
## END SOLUTION

display(sp.Eq(eq1,0))
display(sp.Eq(eq2,0))
display(sp.Eq(eq3,0))
assert(eq1.has(Rbx))
assert((not eq2.has(Rbx)) and (eq2.has(Rby)))
assert((not eq3.has(Rbx)) and (not eq3.has(Rby)))

10.2.5. travail de la réaction du cerceau $Rb$#

Pour calculer le travail fournit par le cerceau pour entraîner la bille, nous allons calculer la puissance de la force de réaction du cerceau $Rb$, i.e. $$ \vec{Rb} . \vec{V_B}$$

En utilisant la méthode .dot() et la vitesse du point B dans $R_0$, calculer la puissance de la réaction $Rb$ et la mettre dans la variable PR
A partir de l’une des équations précédentes, on va remplacer les composantes de $Rb$ par leurs expressips en fonction de $ \theta$ dans PR. Pour cela écrire dans la variable eq l’équation à utiliser.

PR = 0
eq = 0
## BEGIN SOLUTION 
PR = RB.dot(B.vel(R0))
eq = eq2
## END SOLUTION

display("PR=",PR)
display("eq=",eq)
assert(PR != 0)
assert(eq.has(Rby))

10.2.5.1. calcul du potentiel#

En utiisant l’expression de la puissance en fonction de $\theta$, par integration on obtiends le potentiel $Ep_R$ associé en fonction de $\theta$ dans la variable EpR telle que:

\[ \vec{Rb}.\vec{V_B} = -\frac{d\,Ep_R}{dt}\]

# puissance fonction de theta
PR = PR.subs(Rby,sp.solvers.solve(eq,Rby)[0])
display("PR=",PR)
# calcul de l'energie potentiel associee fonction de x
x = sp.symbols('x')
EpR=(-sp.integrate((PR/theta.diff(t)).subs(theta,x),x)).subs(x,theta)
display("EpR=",EpR)

10.3. Simulation numérique#

Le système d’équations précédentes est non linéaire, et sans solution analytique simple. On doit donc le résoudre numériquement.

Pour résoudre numériquement ce système, on se fixe la valeur des paramètres donnés en début de notebook. Définir la valeurs des paramêtres dans la liste valnum, puis substituer dans les equations en utilisant la méthode .subs(valnum) et mettre la valeur dans les variables EQ1 EQ2 EQ3

valnum = [(R,0), (M,0), (g,0), (omega, 0)]
EQ1 = 0
EQ2 = 0
EQ3 = 0
## BEGIN SOLUTION
valnum = [(R,_R), (M,_M), (g,_g), (omega, _omega)]
EQ1 = eq1.subs(valnum)
EQ2 = eq2.subs(valnum)
EQ3 = eq3.subs(valnum)
## END SOLUTION

display("valnum=",valnum)
display(sp.Eq(EQ1,0))
display(sp.Eq(EQ2,0))
display(sp.Eq(EQ3,0))
assert(not (EQ3.has(omega) or EQ3.has(R) or EQ3.has(g) or EQ3.has(M)))

10.3.1. question#

Dans le système précédent :

combien y a t-il d’inconnues, et lesquelles?
quelle est l’équation différentielle à résoudre pour pouvoir obtenir la trajectoire?
quelle est l’interprétation mécanique de cette équation ?
que faut -il se donner en plus pour pouvoir la résoudre

Ecrire votre réponse dans la cellule ci-dessous

10.3.2. analyse du système à résoudre#

écrire vos commentaires ici en répondant aux questions

10.3.3. résolution numérique fonction de $\theta_0$#

Pour résoudre numériquement à l’aide d’une bibliothèque de résolution numérique d’EDO, il faut définir l’expression numérique de certaines quantités

l’équation différentielle à résoudre dans la variable EQ
la position de la bille B dans le repère $R_0$ dans la variable PB
l’énergie cinétique de la bille dans la variable EC et son énergie potentielle dans EP
le potentiel de la force de liaison dans ER

pour cela on utilisera la méthode .subs() pour faire la substitution des valeurs numériques

Les expressions obtenues doivent dépendre uniquement de $\theta$ et de ses dérivées et pas explicitement du temps sauf pour la position de la bille B.

EQ = 0
PB = 0
EC = 0
EP = 0
ER = 0
## BEGIN SOLUTION
EQ = EQ3
PB = B.pos_from(O).express(R0).subs(valnum)
EC = bille.kinetic_energy(R0).subs(valnum)
EP = bille.potential_energy.subs(valnum)
ER = EpR.subs(valnum)
## END SOLUTION

# liste des coordonnées de B
CB = [PB.dot(R0.x), PB.dot(R0.y), PB.dot(R0.z)]
# liste energie cinétique et potentielle
E  = [EC,EP,ER]
display("Eq=",EQ)
display("B=" ,PB)
display("Ec=",EC)
display("Ep=",EP)
display("ER=",ER)
assert(PB.dot(R0.x).free_symbols == {t})
assert(EQ.free_symbols == {t})
assert(EC.free_symbols == {t})
assert(EP.free_symbols == {t})
assert(ER.free_symbols == {t})

On choisit la position initiale de la perle $\theta_0$ et on simule numériquement le mouvement.

On peut modifier la valeur de $\theta_0$ dans la cellule suivante et ensuite re-executer les cellules suivantes pour obtenir la trajectoire.

10.3.4. travail demandée#

pour différentes valeurs de $\theta_0$ ($0$,$\pi/4$,$5\pi/8$, $\pi/2$ , $3\pi/2$ , $\pi$, ..)

refaite la simulation en exécutant les cellules suivantes
attention la valeur numérique de $\pi$ est notée np.pi
analyser le mouvement
tracer certaines quantités en fonction du temps

REM on peut aussi modifier le temps de simulation tmax

# choix de la position initiale
theta0=np.pi
# temps de simulation
tmax = 4

# modèle numérique
BI = Bille(t,theta,EQ,CB, E, _R, _omega)
# resolution 
Y0 = [theta0,0.]
BI.solve(Y0,tmax)

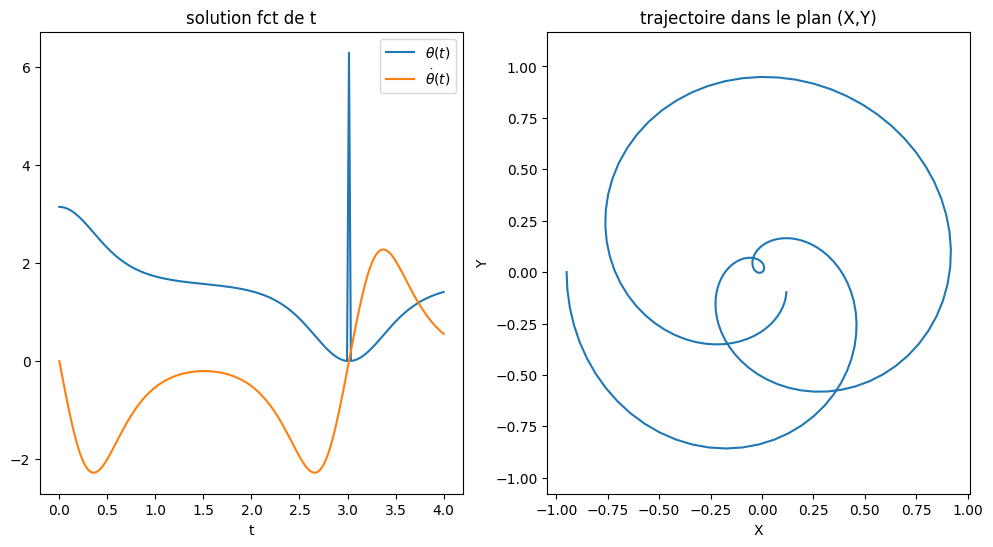
# tracer de la solution 
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(BI.t,BI.THETA,label="$\\theta(t)$")
plt.plot(BI.t,BI.THETAP,label="$\dot{\\theta}(t)$")
plt.legend()
plt.title('solution fct de t')
plt.xlabel('t')
plt.subplot(1,2,2)
plt.plot(BI.XB,BI.YB)
plt.xlabel('X')
plt.ylabel('Y')
plt.title('trajectoire dans le plan (X,Y)')
plt.axis('equal');

# visualisation 3D du mouvement
BI.trace()
BI.trajectoire()

10.3.5. analyse du mouvement#

pour analyser le mouvement on pourra tracer les quantités suivantes issues du calcul

BI.t: les valeurs discretes du temps où la solution est calculée
BI.THETA, BI.THETAP: les valeurs de $\theta$ et $\dot{\theta}$
BI.XB, BI.YB, BI.ZB : les coordonnées de la bille dans R0
BI.EC, BI.EP, BI.ER : l’energie cinétique et potentielle, potentiel force de liaison

pour tracer une quantité en fonction du temps, par exemple BI.ZB

  plt.plot(BI.t,BI.ZB)

## BEGIN SOLUTION
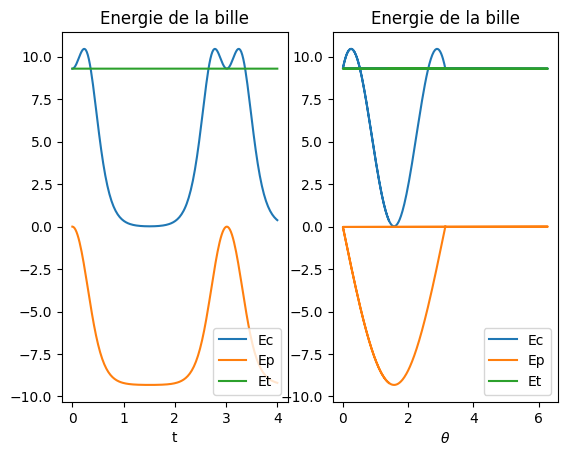
plt.subplot(1,2,1)
plt.title("Energie de la bille")
plt.plot(BI.t,BI.EC,label='Ec')
plt.plot(BI.t,BI.EP,label='Ep')
plt.plot(BI.t,BI.EC + BI.EP + BI.ER,label='Et')
plt.xlabel('t')
plt.legend();
plt.subplot(1,2,2)
plt.title("Energie de la bille")
plt.plot(BI.THETA,BI.EC,label='Ec')
plt.plot(BI.THETA,BI.EP,label='Ep')
plt.plot(BI.THETA,BI.EC + BI.EP + BI.ER,label='Et')
plt.xlabel('$\\theta$')
plt.legend();
## END SOLUTION

10.4. Bilan et compte rendu#

Ecrire un compte rendu sur l’analyse du mouvement en fonction de $\theta_0$