Problème du brachistochrone

10. Problème du brachistochrone#

Ou le chemin le plus rapide n’est pas la ligne droite !

../../_images/brachistochrone.png

Marc Buffat département mécanique Lyon 1

from metakernel import register_ipython_magics
register_ipython_magics()

10.1. Question préliminaire#

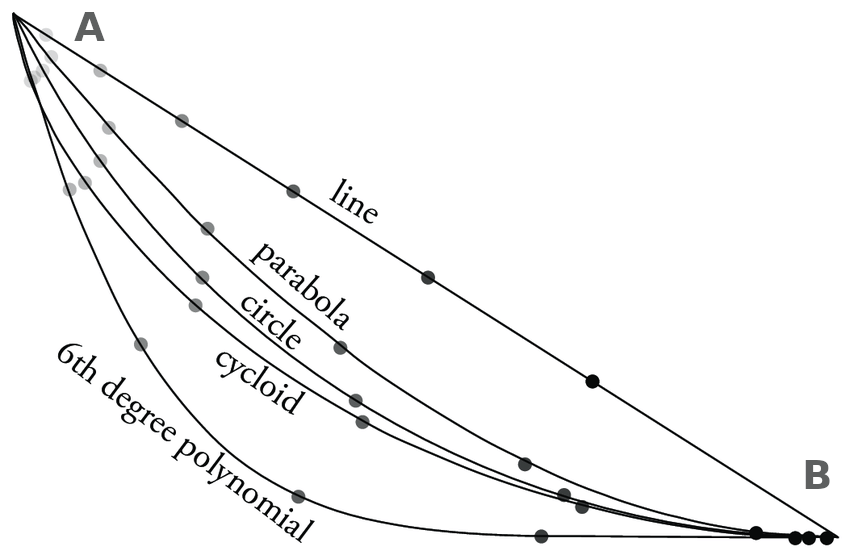
brachistochrone

#%activity /usr/local/commun/ACTIVITY/IntroPython/questionBrachistochrone

%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
# bibliotheque mecanique
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, inertia
from sympy.physics.mechanics import linear_momentum, angular_momentum,cross
from sympy.physics.vector import time_derivative,dot
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
#
from IPython.display import display, Markdown, clear_output
def printmd(string):
    display(Markdown(string))

10.2. Historique: courbe brachistochrone (wikipedia)#

Le mot brachistochrone désigne une courbe dans un plan vertical sur laquelle un point matériel pesant placé dans un champ de pesanteur uniforme, glissant sans frottement et sans vitesse initiale, présente un temps de parcours minimal parmi toutes les courbes joignant deux points fixés : on parle de problème de la courbe brachistochrone.

La résolution du problème de la courbe brachistochrone passionna les mathématiciens de la fin du XVIIe siècle. C’est Jean Bernouilli qui proposa une solution du problème.

10.3. Démarche scientifique#

Etude d’un problème en mécanique

  1. démarche expérimentale: analyse des données (data science)

  2. modélisation: calcul formel (symbolic computation)

  3. simulation: calcul numérique (numerical science)

10.4. Expérience (EPFL)#

from IPython.display import YouTubeVideo 
YouTubeVideo("Z-qaXZeJT4s", width=800, height=460)

10.4.1. Lecture des résultats expérimentaux:#

caméra rapide \(\Rightarrow\) 940 images / sec de 720x1280 pixels

méthode:

  1. on lit la position d’un point de la bille sur l’image (en pixel) sur les images

  2. on convertit la position en metre avec une échelle de référence

  3. on convertit le numéro de l’image en temps

  4. on en déduit la position en fonction du temps, et donc le temps de parcourt

10.4.2. bibliothéque mathplotlib pour les images#

  • img = plt.imread(fichier.png) lecture de l’image dans la variable img

  • plt.imshow(img) affichage de l’image et lecture de la position (en pixel) du curseur

%matplotlib widget
img = plt.imread('images/brachistochroneSolo.png')
plt.imshow(img)

<matplotlib.image.AxesImage at 0x7f38b8fc1900>

10.4.3. Analyse des données#

  • conversion des données (pixel -> metre)

  • revoir le TP sur l’analyse de données météo:

    • droite des moindres carrés

%matplotlib widget
# utilisation de opencv + efficace
import cv2
brac9 = cv2.imread('images/brachistochrone9.png')
plt.imshow(brac9)

<matplotlib.image.AxesImage at 0x7f38e837cca0>

10.5. Modèle: bille sur plan incliné#

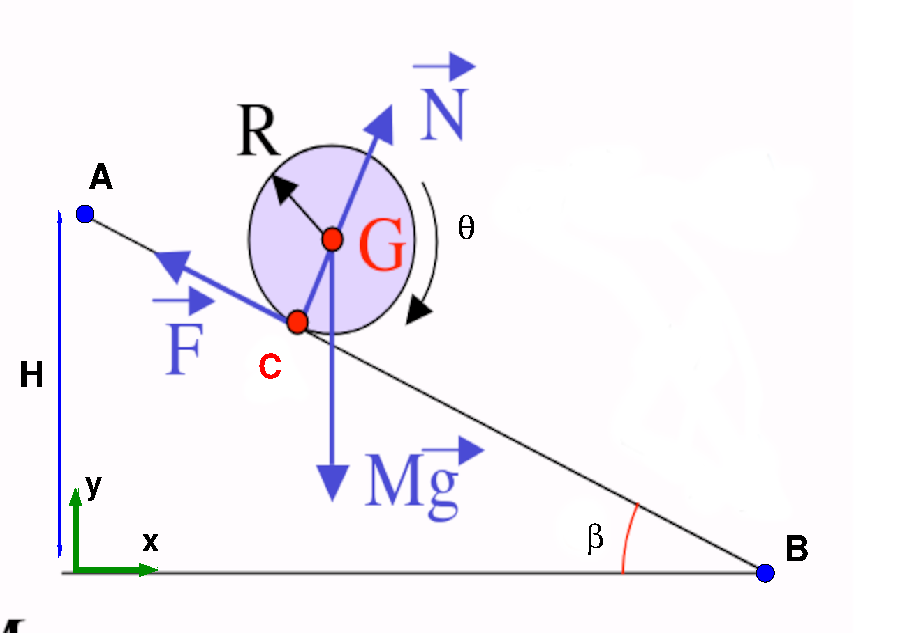
bille_plan

10.5.1. Analyse du problème#

hypothèse: mouvement 2D

  • données du problème:

    • bille pleine homogène \(M,R,H,\beta,g\)

  • bilan des forces:

    • poids \(-Mg \vec{e}_y\) (suivant la verticale)

    • force de contact: (roulement sans glissement) \(\vec{N}=R_n\vec{n}\)

  • 3 degrés de liberté: \(x(t)\),\(y(t)\) et \(\theta(t)\)

inconnues du problème: \(x(t)\),\(y(t)\),\(\theta(t)\) et \(R_n\)

10.5.2. Equations du problème#

Principes fondamentaux de la dynamique

  • variation de la quantité de mouvement = somme des forces apppliquées

  • variation du moment cinétique en G = somme des moments des forces et des couples en G

\(\leadsto\) 3 équations en 2D

  • condition de roulement sans glissement en C: 1 équation

On a bien 4 équations pour 4 inconnues

** Trajectoire imposée **

  • trajectoire de G est fixée: \(y = F(x)\) que l’on écrit sous la forme \(y = H + f(x)\)

  • 2 ddl \(x(t), \theta(t)\)

Le problème est bien posé:

  • on élimine les inconnues de liaison

  • on a 2 ddl indépendantes \(x(t)\) et \(\theta(t)\) (car \(y=F(x)\))

  • on obtiens donc 2 EDO en \(x(t)\) et \(\theta(t)\)

    • dans le cas d’une droite: solution analytique

    • dans le cas général: solution numérique

Propriétés du système

  • travail d’une force ou sa puissance (travail / unité de temps) $\( W = \vec{F}.\vec{dC} \mbox{ ou } P = \vec{F}.\vec{V}_C \)$

  • La seule force qui travaille = gravité, qui découle d’un potentiel

  • Le système est donc conservatif

  • Il transforme de l’énergie potentielle en énergie cinétique

10.6. modèle: roulement sans glissement d’une bille sur une courbe#

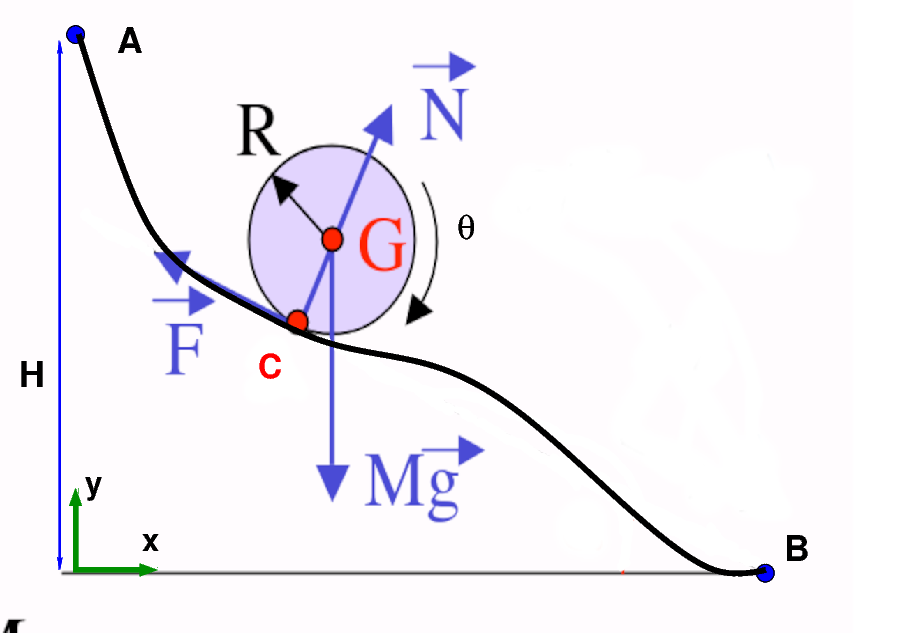
bille_plan

  • on définit un repère fixe R0 (x,y,z) et un repère R1 lié à la bille.

  • la trajectoire de la bille est la courbe \(y=H+f(x)\) reliant A à B de hauteur H

  • la fonction \(f(x)\) est telle que \(f(0)=0\) et \(f(0)=-H\)

  • la bille roule sans glissement sur la courbe

  • la bille est une sphère homogène de rayon R et de masse M

10.6.1. paramètres et ddl#

  • les paramètres du problème sont : R,M,g , H et l’équatio de la courbe \(y=H+f(x)\)

  • les degrés de liberté sont \(x(t),y(t)\) (position en x,y du centre de gravité G) et \(\theta(t)\) (angle de rotation de la bille autour de z)

  • les degrés de liberté \(x(t),y(t)\) sont liés par la forme de la trajectoire: \(y = H+f(x)\).

  • on a donc uniquement 2 degrés de liberté indépendants, et il faut donc 2 équations.

Par exemple pour une trajectoire sur un plan inclinée d’angle \(\beta\) $\( y(t) = H - \tan\beta\; x(t)\)$

La trajectoire \(f(x)=- \tan\beta\; x\) vérifie de plus les 2 conditions suivantes :

\[y=H+f(x) \mbox{ tq. } y(0)=H \mbox{ et } y(x_1)= 0\]

10.6.2. calcul de la tangente et la normale#

au point de contact C on peut calculer la tangente \(\vec{t}\) et la normale \(\vec{n}\) à la courbe en fonction de \(f(x)\) et de \(\frac{df}{dx}\) (on donnera une explication dans le compte rendu)

\[\begin{split} \vec{t} = \begin{bmatrix} \frac{1}{\sqrt{1 + \frac{df}{dx}^2}}\\ \frac{\frac{df}{dx}}{\sqrt{1 + \frac{df}{dx}^2}} \end{bmatrix} \mbox{ et }\vec{n} = \begin{bmatrix} \frac{-\frac{df}{dx}}{\sqrt{1 + \frac{df}{dx}^2}}\\ \frac{1}{\sqrt{1 + \frac{df}{dx}^2}} \end{bmatrix} \end{split}\]

10.6.3. condition de roulement sans glissement#

La condition de roulement sans glissement de la bille sur la courbe impose que la vitesse de la bille au point de contact C doit être nulle.

En appliquant la composition de mouvement pour un point P de la bille $\( \vec{V}_{P/R_0} = \vec{V}_{G/R_0} + \vec{V}_{P/R_1}\)$

\[ \vec{V}_{P/R_0} = (\frac{R \frac{d}{d t} \theta{\left(t \right)}}{\sqrt{\left(\frac{d}{d x{\left(t \right)}} f{\left(x{\left(t \right)} \right)}\right)^{2} + 1}} + \frac{d}{d t} x{\left(t \right)})\mathbf{\vec{e}_x} + (\frac{R \frac{d}{d x{\left(t \right)}} f{\left(x{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)}}{\sqrt{\left(\frac{d}{d x{\left(t \right)}} f{\left(x{\left(t \right)} \right)}\right)^{2} + 1}} + \frac{d}{d x{\left(t \right)}} f{\left(x{\left(t \right)} \right)} \frac{d}{d t} x{\left(t \right)})\mathbf{\vec{e}_y} \]

on obtiens la valeur de la vitesse de glissement en faisant \(P=C\). Cette vitesse est forcément tangente à la trajectoire. La condition de roulement sans glissement impose donc que la vitesse tangentielle pour \(P=C\) est nulle, ce qui fournit une première équation du mouvement.

Avec ces notations on obtiens la première équation du mouvement:

\[ \frac{d}{d t} x{\left(t \right)} = - \frac{R \frac{d}{d t} \theta{\left(t \right)}}{\sqrt{\left(\frac{d}{d x{\left(t \right)}} f{\left(x{\left(t \right)} \right)}\right)^{2} + 1}} \]

10.6.4. Conservation de l’énergie#

Le système étant conservatif, l’énergie totale \(E_t\), somme de l’énergie cinétique et de l’énergie potentielle \(U_p\), se conserve.

\[ Ec = \frac{M}{2} R^2 \dot{\theta}^2 + \frac{M}{2}(\dot{x}^2 + \dot{y}^2) = \frac{7 M R^{2} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2}}{10} \mbox{ , } Up = M g y\]

On montre que cette énergie totale \(E_t\) s’écrit (on le justifiera dans le compte-rendu) et est constante et égale à la valeur initiale: $\( E_t = \frac{7 M R^{2} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2}}{10} + M g (H+f{\left(x{\left(t \right)} \right)}) = Mg H \)$

On obtiens la deuxième équation du mouvement: $\( \frac{d}{d t} \theta{\left(t \right)} = - \frac{\sqrt{70} \sqrt{- g f{\left(x{\left(t \right)} \right)}}}{7 R} \)$

10.6.5. Equations du mouvement#

De l’étude précédente, on en déduit les 2 equations du mouvement.

En notant \(Y(t)\) le vecteur inconnu:

\[\begin{split} Y(t) = \begin{pmatrix} x(t) \\ \theta(t) \end{pmatrix} \end{split}\]

le système à résoudre s’écrit:

\[\begin{split}\dot{Y} = \mathbf{F}(Y) \mbox{ avec } \mathbf{F}(Y) = \begin{pmatrix} \frac{\sqrt{-\frac{10}{7} g f(x)}}{\sqrt{1+ (\frac{df}{dx})^2}}\\ \frac{- \sqrt{-\frac{10}{7} g f(x)}}{ R}\\ \end{pmatrix} \end{split}\]

où \(f(x)\leq 0\) et vérifie : \(f(0)=0\) et \(f(x_B)=-H\) car \(y=H+f(x)\)

A ces équations, on ajoute les conditions initiales:

\[x(0)=0 \mbox{ et } \theta(0) = 0 \]

10.7. Solution analytique#

dans le cas d’une droite \(f(x) = - x\tan\beta \), on a la conservation de l’énergie s’écrit

\[ \frac{7 M R^{2} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2}}{10} = M g x \tan\beta \]

et l’équation de roulement sans glissement

\[\frac{d}{d t} x{\left(t \right)} = - \frac{R \frac{d}{d t} \theta{\left(t \right)}}{\sqrt{\tan^2\beta + 1}} \]

En éliminant \(\theta\) dans la première il vient:

\[ \frac{7}{10} (1+\tan^2\beta)(\frac{d}{d t} x{\left(t \right)})^2 = g x \tan\beta \]

en différentiant et en simplifiant par \(\frac{d x}{d t}\), il vient :

\[\frac{7}{5} (1+\tan^2\beta)\frac{d^2}{d t^2} x(t) = g \tan\beta \]

dont la solution s’écrit:

\[x(t) = \frac{5}{14} g \;t^2 \frac{\tan\beta}{1+\tan^2\beta} = \frac{5}{14} g \;t^2 \sin\beta\cos\beta \]

10.8. Solution numérique#

On écrit le système précédent sous forme vectorielle en notant $\( Y = \begin{pmatrix} x \\ \theta \end{pmatrix} \)$

solution de l’EDO

\[\begin{split}\dot{Y} = \mathbf{F}(Y) \mbox{ avec } \mathbf{F}(Y) = \begin{pmatrix} \frac{\sqrt{-\frac{10}{7} g f(x)}}{\sqrt{1+ (\frac{df}{dx})^2}}\\ \frac{- \sqrt{-\frac{10}{7} g f(x)}}{ R}\\ \end{pmatrix}\end{split}\]

la trajectoire est fixée t.q.: $\(y=H+f(x) \mbox{ tq. } y(0)=0 \mbox{ et } y(x_B)=-H\)$

10.9. Référence#

  • [Sanchis (2014)] Gabriela R. Sanchis, Historical Activities for Calculus,Convergence, July 2014.

%%activity /usr/local/commun/ACTIVITY/IntroPython/questionBrachistochrone
{"activity": "poll",
 "instructors": ["buffat","marc.buffat","cours"],
 "items": [
      {"id": "0", 
       "question":  """Quel est le chemin le plus rapide pour une bille allant de A à B par effet de gravité""", 
       "type": "multiple choice",
       "options": [ """la ligne droite""", 
                    """la parabole""", 
                    """le cercle""",                    
                    """la cycloide""",
                    """le pôlynome de degré 6"""
                  ]
      },
 ]}
Contenu