TP Cinématique et trajectoires

4. TP Cinématique et trajectoires#

Marc Buffat, dpt mécanique, UCB Lyon 1

../../../../_images/piste_velo.jpg

Attention il faut exécuter toutes les cellules suivantes pour afficher son nom !!

%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from validation.valide_markdown import test_markdown, test_code
from validation.validation import info_etudiant, bib_validation
from IPython.display import display, Markdown, clear_output

# nom etudiant
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if NUMERO_ETUDIANT is None:
    NOM,PRENOM,NUMERO_ETUDIANT = info_etudiant()
printmd("## Etudiant {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
# generation des 2 circuits
bib_validation('cours','MGC2028L')
from Circuit import Circuit,Circuit2,test_vitesse,test_trajectoire,test_acceleration
np.random.seed(NUMERO_ETUDIANT)
Circuit("circuit.txt");
np.random.seed(NUMERO_ETUDIANT)
Circuit2("circuit2.txt");

try:
    printmd("INITIALISATION OK!")
except:
    print("Erreur vous n'avez pas executée la cellule vide précédente !")
    print("Votre Notebook n'est pas initialisé correctement !")

4.1. Objectif#

L’objectif du TP est d’étudier la cinématique d’un cycliste sur piste à partir de mesures de sa vitesse en fonction du temps.

Dans un fichier, on a le relevé des 2 composantes de la vitesse horizontale en fonction du temps. A partir de ces mesures, on doit:

  • détermination de la vitesse moyenne

  • reconstruire la trajectoire du cycliste

  • calculer les composantes de l’accélération, en particulier l’accélération tangentielle et l’accélération centripète

  • déterminer l’inclinaison du cycliste pour compenser la force centrifuge

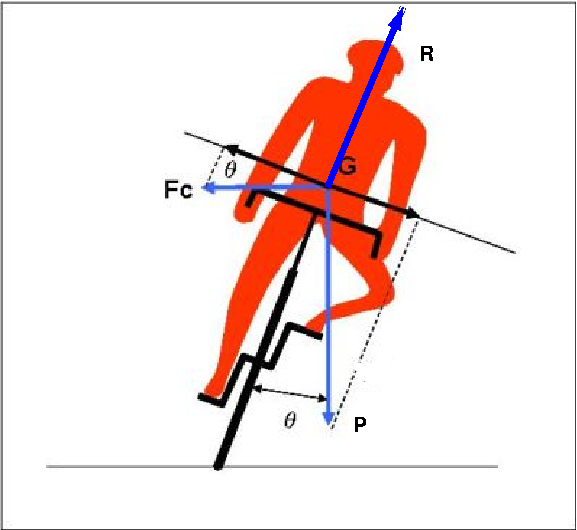
../../../../_images/cycliste1.png

On veut calculer l’angle \(\theta\) d’inclinaison du cycliste, qui correspond à l’équilibre des forces dans le référentiel lié au cycliste dans le plan de la figure:

\[ \vec{F_c} + \vec{P} + \vec{R} = \vec{0}\]

La force centrifuge \(\vec{F_c} = - M \vec{\gamma_n}\) est une force fictive qui est opposée à l’accélération dans la direction normale, et qui traduit cet équilibre statique dans le référentiel lié au cycliste. Dans le référentiel fixe, on retrouve le PFD dans le plan de la figure:

\[ \vec{F_c} + \vec{P} = M \vec{\gamma_n}\]

Remarque dans la direction tangentielle (i.e. la direction perpendiculaire au plan de la figure) on a un équilibre entre l’accélération tangentielle, la force de traction, et les forces de frottements.

Pour calculer \(\theta\), il faut donc calculer l’accélération tangentielle et normale, i.e. le vecteur accélération projeté dans le référentiel local directe formé par la tangente et la normale en chaque point de la trajectoire.

4.2. Compte rendu#

En plus du notebook vous devez écrire un compte rendu au format markdown dans le fichier CompteRendu.md puis à la fin du notebook vous avez les instructions pour générer une version en html dans CompteRendu.html.

4.3. Analyse du 1er circuit elliptique#

Les données du premier circuit sont dans le fichier circuit.txt qui contient 3 colonnes correspondants au temps (en s.), et aux 2 composantes de la vitesse suivant x et y (en m/s).

4.3.1. lecture des données de vitesse#

Dans la cellule suivante:

  1. lire les données à partir du fichier en utilisant la fonction loadtxt et les mettre dans les 3 tableaux T,U,V

  2. à partir des composantes U et V calculer la norme Um de la vitesse en km/h

  3. déterminer Umean la moyenne de Um , son minimum Umin et son maximum Umax. On pourra utiliser les fonctions (méthodes) numpy: mean(), max() et min()appliquées aux tableaux.

  4. tracer Um en fonction du temps et sauvegarder la courbe dans un fichier, que vous devez inclure ensuite dans votre contre rendu.

  5. pour un cycliste chevronné, commenter l’ordre de grandeur des vitesses calculées.

Remarque: dans la suite on travaillera avec des vitesses en unité SI (m/s)

T = None
U = None
V = None
Umean = None
Umin  = None
Umax  = None
### BEGIN SOLUTION
#plt.savefig("vitesse.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((U.size == T.size) and (V.size == T.size))
print("Vitesse moyenne={:.1f}km/h min={:.1f} km/h max={:.1f}km/h".format(Umean,Umin,Umax))
assert(test_vitesse("circuit.txt",Umean,Umin,Umax))

4.3.2. Calcul de la trajectoire#

A partir des composantes de vitesse U et V , calculer la trajectoire en fonction du temps, i.e. la position \(X_i\) et \(Y_i\) du point \(P_i\) de la trajectoire pour chacun des temps \(T_i\). Connaissant la position \(\mathbf{P}_{i-1}:(X_{i-1},Y_{i-1})\) et la vitesse \(\vec{U}_{i-1}:(U_{i-1},V_{i-1})\) à l’instant précédent \(T_{i-1}\), on peut en déduire simplement la nouvelle position \(\mathbf{P}_{i}:(X_{i},Y_{i})\)

\[ \mathbf{OP}_{i} \approx \mathbf{OP}_{i-1} + \vec{U}_{i-1} dt \leadsto X_{i} = X_{i-1} + U_{i-1} dt , Y_{i} = Y_{i-1} + V_{i-1} dt \]

L’approximation obtenue est uniquement d’ordre 1 et n’utilise pas toute l’information disponible. En effet on connaît la vitesse à l’instant \(T_{i-1}\) mais aussi \(T_i\). Une meilleur approximation de la vitesse entre \(T_{i-1}\) et \(T_i\) est de choisir la vitesse moyenne calculée comme moyenne de la vitesse à \(T_{i-1}\) et \(T_i\)

\[ \mathbf{OP}_{i} \approx \mathbf{OP}_{i-1} + \frac{1}{2}(\vec{U}_{i-1}+\vec{U}_{i-1}) dt \leadsto X_{i} = X_{i-1} + \frac{1}{2}(U_{i-1}+U_i) dt , Y_{i} = Y_{i-1} + \frac{1}{2}(V_{i-1}+V_i) dt \]

On utilisera dans la suite cette relation pour calculer la trajectoire.

Dans la cellule suivante:

  1. calculer la position des points de la trajectoire dans les 2 vecteurs numpy X et Y

  2. en déduire la longueur de la trajectoire dans la variable L

  3. tracer la trajectoire (X,Y) ainsi que la vitesse sur le même graphe et sauvegarder la courbe dans un fichier, que vous devez inclure ensuite dans votre compte rendu.

  4. comparer le calcul de L avec un calcul utilisant la vitesse moyenne précédente

On utilisera la fonction plt.quiver(X,Y,U,V) qui permet de tracer des flèches de longueur U,V aux points X,Y. Pour éviter de tracer trop de flèches, on pourra prendre par exemple un point sur 10 en remplaçant X par X[::10] et idem pour tous les autres arguments.

### X = None
Y = None
L = None
### BEGIN SOLUTION
# calcul longueur
# tracer
#plt.savefig("trajectoire.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((X.size == T.size) and (Y.size == T.size))
print("Longueur du circuit {:.2f}m".format(L))
assert(test_trajectoire("circuit.txt",X,Y,L))
assert(test_code("TP_trajectoire.ipynb","cell-verif1",["plt.plot","plt.quiver","plt.title"]))

4.3.3. Calcul de l’accélération#

On se propose de calculer l’accélération tangentielle et normale, i.e. le vecteur accélération projeté dans le référentiel local direct formé par la tangente et la normale en chaque point de la trajectoire.

Dans la cellule suivante:

  1. Calculer les composantes suivant x et y de l’accélération au milieu de chacun des segments \([T_{i},T_{i+1}]\) de la trajectoire, en utilisant l’accroissement de vitesse suivant x et suivant y. On mettra le résultat dans les vecteurs numpy Gmx et Gmy respectivement. L’accélération sur le ième segment \([T_{i},T_{i+1}]\) s’écrit:

\[ Gmx_i = \frac{\Delta U}{\Delta t} = \frac{U_{i+1} - U_{i}}{T_{i+1} - T_{i}}, Gmy_i = \frac{\Delta V}{\Delta t} = \frac{V_{i+1} - V_{i}}{T_{i+1} - T_{i}}\]

on calculera le temps au milieu du ième segment comme moyenne de \([T_{i}\) et \(T_{i+1}]\) dans le vecteur \(Tm\)

\[ Tm_i = \frac{T_{i+1}+T_{i}}{2} \]

  1. Calculer en chacun de ces points milieu les composantes suivant x et y de la tangente (vecteur unitaire) dans les vecteurs numpy Tmx et Tmy. En déduire les composantes de la normale (vecteur unitaire) dans Ǹmx et Ǹmy tel que le repétre (\(\vec{t},\vec{n},\vec{e_z}\)) soit orthonormé direct. On pourra calculer la vitesse moyenne sur chaque segment pour ce calcul.

  2. Calculer par projection la composante de l’accélération tangentielle et celle de l’accélération normale à chaque instant \(Tm_i\). On mettra le résultat dans les vecteurs Gmt et Gmn.

  3. En déduire l’angle d’inclinaison \(\theta\) en degré du cycliste pour composer la force centrifuge en prenant \(g=9.81\). On mettra le résultat dans le tableau numpy THETA. On pourra utiliser la fonction numpy arctan2(a,b) qui calcule l’angle en radian dont la tangente vaut \(a/b\).

  4. Tracer les 2 composantes d’accélérations tangentielles et normales normalisées par \(g\) en fonction du temps, ainsi que l’angle d’inclinaison du cycliste et sauvegarder la courbe dans un fichier, que vous devez inclure ensuite dans votre contre rendu.

  5. Commenter l’ordre de grandeur de l’angle d’inclinaison \(\theta\), et discuter sa variation. Commenter la variation de l’accélération tangentielle.

Gmx = None
Gmy = None
Tmx = None
Tmy = None
Nmx = None
Nmy = None
Gmt = None
Gmn = None
THETA = None
### BEGIN SOLUTION
# temps
# calcul de la moyenne de la vitesse 
#
# calcul de l'angle
# tracer
#plt.savefig("acceleration.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((Gmx.size == T.size-1) and (Gmy.size == T.size-1))
assert((Tmx.size == T.size-1) and (Tmy.size == T.size-1))
assert((Gmn.size == T.size-1) and (Gmt.size == T.size-1))
assert(THETA.size == T.size-1)
assert(test_acceleration("circuit.txt",Gmt/g,Gmn/g,THETA))
assert(test_code("TP_trajectoire.ipynb","cell-verif2",["plt.plot","plt.title"]))

4.4. Analyse du circuit2 de type Lemniscate#

Les données du second circuit sont dans le fichier circuit2.txt qui contient 3 colonnes correspondants au temps (en s.), et aux 2 composantes de la vitesse suivant x et y (en m/s).

On vous demande de refaire la même analyse que pour le premier circuit elliptique.

4.4.1. lecture des données de vitesse#

Dans la cellule suivante:

  1. lire les données à partir du fichier en utilisant la fonction loadtxt et les mettre dans les 3 tableaux T2,U2,V2

  2. déterminer l’amplitude de la vitesse moyenne U2mean, de la vitesse min U2min et de la vitesse max U2max en km/h

  3. tracer l’amplitude de la vitesse en fonction du temps et sauvegarder la courbe dans un fichier, que vous devez inclure ensuite dans votre contre rendu.

T2 = None
U2 = None
V2 = None
U2mean = None
U2min  = None
U2max  = None
### BEGIN SOLUTION
#plt.savefig("vitesse2.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((U2.size == T2.size) and (V2.size == T2.size))
print("Vitesse moyenne={:.1f}km/h min={:.1f} km/h max={:.1f}km/h".format(U2mean,U2min,U2max))
assert(test_vitesse("circuit2.txt",U2mean,U2min,U2max))
assert(test_code("TP_trajectoire.ipynb","cell-verif3",["plt.plot","plt.title"]))

4.4.2. Calcul de la trajectoire#

A partir des composantes de vitesse U2 et V2 , calculer la trajectoire en fonction du temps, i.e. la position \(X2_i\) et \(Y2_i\) pour chacun des temps \(T2_i\) en utilisant la meme analyse que pour le circuit 1.

X2 = None
Y2 = None
L2 = None
### BEGIN SOLUTION
# calcul longueur
# tracer
# plt.savefig("vitesse2.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((X2.size == T2.size) and (Y2.size == T2.size))
print("Longueur du circuit {:.2f}m".format(L2))
assert(test_trajectoire("circuit2.txt",X2,Y2,L2))
assert(test_code("TP_trajectoire.ipynb","cell-verif4",["plt.plot","plt.title","plt.quiver"]))

4.4.3. Calcul de l’accélération#

Calculer l’accélération tangentielle et normale, i.e. le vecteur accélération projeté dans le référentiel local directe formé par la tangente et la normale en chaque point de la trajectoire en utilisant la même analyse que pour le premier circuit.

G2mx = None
G2my = None
T2mx = None
T2my = None
N2mx = None
N2my = None
G2mt = None
G2mn = None
THETA2 = None
### BEGIN SOLUTION
#
# temps
# calcul de la moyenne de la vitesse 
#
# calcul de l'angle
# tracer
#plt.savefig("acceleration2.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((G2mx.size == T2.size-1) and (G2my.size == T2.size-1))
assert((T2mx.size == T2.size-1) and (T2my.size == T2.size-1))
assert((G2mn.size == T2.size-1) and (G2mt.size == T2.size-1))
assert(THETA2.size == T2.size-1)
assert(test_acceleration("circuit2.txt",G2mt/g,G2mn/g,THETA2))
assert(test_code("TP_trajectoire.ipynb","cell-verif5",["plt.plot","plt.title"]))

4.5. Mouvement d’un disque en rotation#

On veut maintenant étudier le mouvement d’un point d’un disque en rotation uniforme et dont l’axe de rotation décrit le circuit précédent avec la même vitesse que le cycliste.

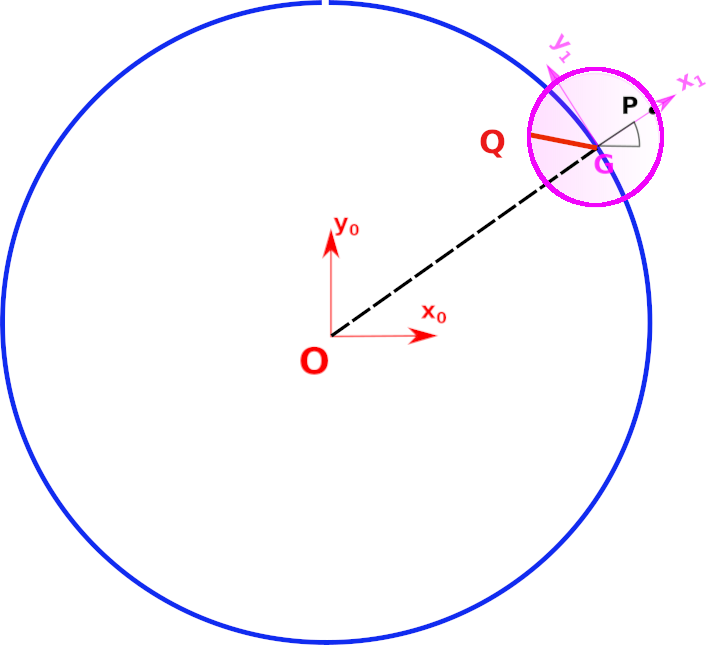
../../../../_images/mvt_planete1.png

Le disque a un rayon \(R\) de 10m. La période de rotation du disque est égale à 1/10e du temps de parcours de la trajectoire.

Dans la cellule suivante, calculer la vitesse relative d’un point du disque à chaque instant t dans le tableau T2, projetée dans le référentiel fixe, et on écrira le résultat dans les tableaux Ur et Vr.

Tracer l’évolution de cette vitesse en fonction du temps.

R = 10
Ur = 0
Vr = 0
## BEGIN SOLUTION
## END SOLUTION

# test sur les résultats (a executer)
assert((Ur.size == T2.size) and (Vr.size == T2.size))
assert(np.allclose(Ur**2+Vr**2 , (Ur[0]**2+Vr[0]**2)))

4.5.1. Composition de mouvement#

En utilisant la composition du mouvement, calculer la vitesse absolue de ce point du disque projetée dans le référentiel fixe. Le résultat sera écrit dans les tableaux Ud et Vd.

  • calculer la vitesse moyenne Udmean

  • calcul la valeur min et max dans Udmin et Udmax

Ud = 0
Vd = 0
Udmean = None
Udmin  = None
Udmax  = None
### BEGIN SOLUTION
#plt.savefig("vitessed.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((Ud.size == T2.size) and (Vd.size == T2.size))
print("Vitesse moyenne={:.1f}km/h min={:.1f} km/h max={:.1f}km/h".format(Udmean,Udmin,Udmax))
assert(test_code("TP_trajectoire.ipynb","cell-verif7",["plt.plot","plt.title"]))

4.5.2. Calcul de la trajectoire#

A partir des composantes de vitesse Ud et d2 , calculer la trajectoire en fonction du temps, i.e. la position \(Xd_i\) et \(Yd_i\) pour chacun des temps \(T2_i\). On utilisera la même analyse que précédemment

Xd = None
Yd = None
Ld = None
### BEGIN SOLUTION
# calcul longueur
# tracer
# plt.savefig("vitesse2.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((Xd.size == T2.size) and (Yd.size == T2.size))
print("Longueur du circuit {:.2f}m".format(Ld))
assert(test_code("TP_trajectoire.ipynb","cell-verif8",["plt.plot","plt.quiver","plt.title"]))

4.5.3. Calcul de l’accélération#

Calculer l’accélération tangentielle et normale, i.e. le vecteur accélération projeté dans le référentiel local directe formé par la tangente et la normale en chaque point de la trajectoire. On utilisera la même analyse que précédemment.

Gdmx = None
Gdmy = None
Tdmx = None
Tdmy = None
Ndmx = None
Ndmy = None
Gdmt = None
Gdmn = None
### BEGIN SOLUTION
#
# temps
# calcul de la moyenne de la vitesse 
# normalisation
# tracer
#plt.savefig("accelerationd.png")
### END SOLUTION

# test sur les résultats (a executer)
assert((Gdmx.size == T2.size-1) and (Gdmy.size == T2.size-1))
assert((Tdmx.size == T2.size-1) and (Tdmy.size == T2.size-1))
assert((Gdmn.size == T2.size-1) and (Gdmt.size == T2.size-1))
assert(test_code("TP_trajectoire.ipynb","cell-verif9",["plt.plot","plt.title"]))

4.6. Bilan#

Ecrire votre analyse et votre conclusion dans le compte rendu en insistant sur

  1. Description de la méthode d’analyse

  2. Résultat de l’analyse

  3. Conclusion

Le compte rendu est à écrire dans le fichier CompteRendu.md

  1. Génération de la version HTML du Compte Rendu (avec mise en page)

  • Exécution de la commande ci-dessous pour générer le fichier html

  1. Visualisation du Compte Rendu (version html)

  • Cliquez sur le lien suivant après exécution de la commande ci-dessous

  • Cliquez sur le bouton mise à jour du navigateur pour mettre à jour la page web

# génération de la version html du CR
!genereTPhtml CompteRendu

# test sur les commentaires (a executer)
assert(test_markdown('CompteRendu.md',None,minm=200,maxe=0.25))

4.7. FIN#
Contenu