Cinématique et calcul de trajectoire

3. Cinématique et calcul de trajectoire#

%matplotlib inline
import numpy as np
import sympy as sp
from sympy.plotting import plot
import matplotlib.pyplot as plt
# police des titres
plt.rc('font', family='serif', size='18')
from IPython.core.display import HTML
from IPython.display import display
from metakernel import register_ipython_magics
register_ipython_magics()
from validation.valide_markdown import test_markdown, test_code
from validation.validation import info_etudiant, bib_validation
from IPython.display import display, Markdown, clear_output

3.1. Rappel: dérivée d’un vecteur#

soit \(\vec{U}\) un vecteur de \(R^3\), on veut calculer sa dérivée par rapport au temps

On connaît les composantes du vecteur dans un référentiel \(\vec{e}_1, \vec{e}_2, \vec{e}_3\) du référentiel $\( \vec{U} = u_1 \vec{e}_1 + u_2 \vec{e}_2 + u_3 \vec{e}_3\)$

Que vaut sa dérivée : $\(\frac{d\vec{U}}{dt}\)$

3.2. Rappel: trajectoire circulaire:#

  1. rotation de la terre autour de son axe: mouvement d’un point sur la terre

  2. mouvement de la terre/ soleil: modèle simplifié d’une planéte (mouvement héliocentrique de Copernic)

3.2.1. Mise en équations#

  • cercle de rayon a

\[ (\frac{x}{a})^2 + (\frac{y}{a})^2 = 1 \]

  • mouvement uniforme de taux de rotation \(\omega\)

    \[ x(t) = a \cos\omega t \mbox{ et } y(t) = a \sin\omega t \]

3.2.2. Questions sur le mvt circulaire#

Cinématique 1

  • Cinématique mvt circulaire

3.3. Rappel: trajectoire elliptique#

Mouvement héliocentrique des planétes de Kepler

  • a,b axes de l’ellipse x,y coordonnées / centre O

\[xp = a \cos{\theta} \mbox{ et } yp = b \sin{\theta} \]

  • trajectoire = ellipse de rayon \(a,b\) avec \(a>b>0\)

Loi des aires: 2nde loi de Kepler

Les planétes décrivent des ellipses et le soleil se trouve sur un des foyers (périhélie)

Soit \(A(t)\) l’aire de la surface balayée par le rayon vecteur \(r_e\) durant le mouvement d’une planète, alors cette seconde loi stipule que des aires égales sont balayées dans des temps égaux.

La loi des aires impose la variation de l’angle en fonction du rayon par rapport au foyer \(r_e(t)\) et donc du temps

\[\frac{1}{2} r_e^2 d\theta = cste\]

ce qui implique:

\[\dot{\theta} = r_e^{-2}\]

3.3.1. Questions sur le mvt elliptique#

Cinématique 2

  • Cinématique mvt circulaire

3.4. Rappel: mvt d’un point sur la terre#

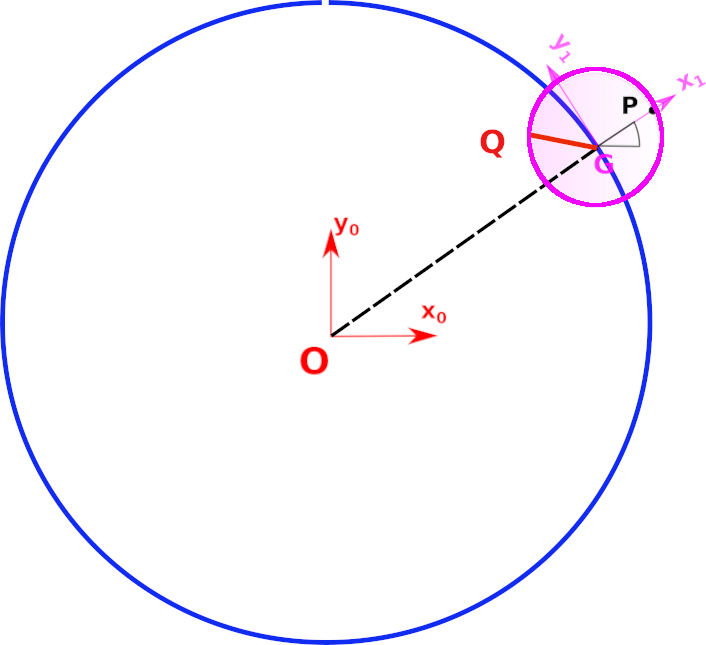
../../../../_images/mvt_planete2.png

3.4.1. Questions sur le mvt d’un point sur la terres#

Cinématique 3

  • Cinématique mvt circulaire

3.5. Trajectoire en 1D#

On veut calculer la distance de freinage et arrêt d’un véhicule à partir de mesure de la vitesse de freinage.

Sur autoroute, une voiture roule à une vitesse \(U_0=110 km/h\) et elle doit brutalement s’arrêter. Après un temps de réaction \(tr\) d’une seconde, le conducteur appuie sur le frein et la voiture passe de 110 km/h à 0 km/h en un temps \(t_f\) de 10 secondes avec la loi de vitesse suivante, donnée dans les 2 tableaux T et U.

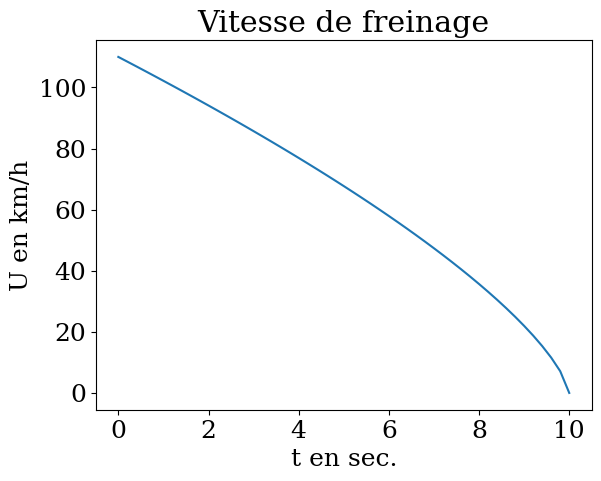
  • tracée la loi de vitesse en fonction du temps

# données du problème
U0 = 110.
tf = 10.0
tr = 1.0
T  = np.linspace(0,tf,51)
U  = U0*((1. - T/tf)**0.7)

# trace de la vitesse
## BEGIN SOLUTION
plt.plot(T,U)
plt.xlabel("t en sec.")
plt.ylabel("U en km/h")
plt.title("Vitesse de freinage")
## END SOLUTION

Text(0.5, 1.0, 'Vitesse de freinage')
../../../../_images/b8e6d7d0e55d1f4b669d672af7c010b54f0b51d011399aa54c7405971b04051f.png

3.5.1. calcul de la distance de freinage#

A partir de la vitesse U, calculer la distance parcourue en fonction du temps, i.e. la position \(X_i\) pour chacun des temps \(T_i\).

Sur chaque intervalle \([T_{i-1},T_i]\), on utilisera la vitesse moyenne pour calculer la position \(X_i\) à l’instant \(T_i\) en fonction de la position précédente \(X_{i-1}\) à \(T_{i-1}\), i.e.

\[ X_{i} \approx X_{i-1} + \bar{U} dt = X_{i-1} + \frac{(U_{i} + U_{i-1})}{2} (T{i}-T_{i-1}) \]

Attention aux unités

  • En déduire la distance de freinage dans la variable xf.

  • En déduire la distance d’arrêt dans la variable xa

  • Au bout de combien de temps, parcourt-on la moitié de cette distance , i.e. xf/2

indication Pour recherche dans le tableau X, l’indice du point le plus proche d’une valeur val, on peut utiliser la fonction np.argmin() qui renvoie l’indice du minimum d’un tableau passé en argument.

# calcul de la distance
N = 0
X = None
## BEGIN SOLUTION
N = T.size
X = np.zeros(N)
for i in range(1,N):
    Um = 0.5*(U[i]+U[i-1])/3.6
    X[i] = X[i-1] + Um*(T[i]-T[i-1])
# distance freinage
xf = X[-1]
xa = xf + tr*U0/3.6
print("distance de freinage : {:.2f} m distance d'arret : {:.2f} m".format(xf,xa))
i2 = np.argmin(np.abs(X-xf/2))
print("distance xf/2 ={:.2f} m à t={:.2f} s".format(X[i2],T[i2]))
## END SOLUTION

distance de freinage : 179.69 m distance d'arret : 210.24 m
distance xf/2 =91.05 m à t=3.40 s

3.5.2. calcul de la décélération en g#

Calculer la décélération sur chacun des segments \([T_{i},T_{i+1}]\) de la trajectoire, en utilisant l’accroissement de vitesse. On mettra le résultat dans le vecteurs numpy G.

On utilisera pour unité le G (i.e. on adimensionne le résultat avec l’accélération de la pesanteur \(g=9.81 m s^{-2}\))

\[ G_i = \frac{\Delta U}{\Delta t} = \frac{U_{i+1} - U_{i}}{T_{i+1} - T_{i}}\]

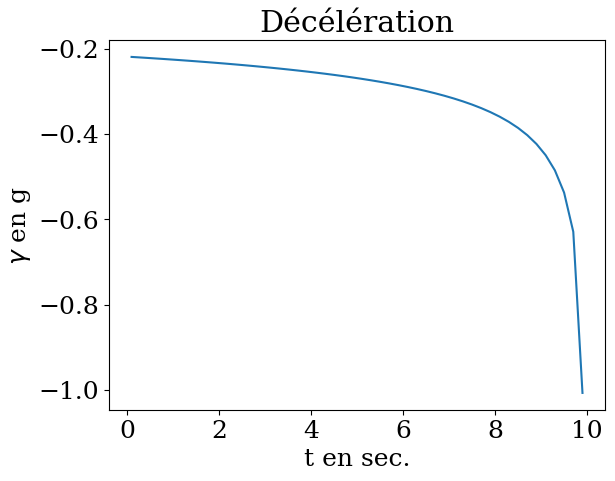
Tracer le résultat et commenter

# calcul décélération en g
g = 9.81
G = None
## BEGINS OLUTION
G = np.zeros(N-1)
Tm = np.zeros(N-1)
for i in range(0,N-1):
    dU = (U[i+1]-U[i])/3.6
    dT = T[i+1]-T[i]
    G[i] = (dU/dT)/g
    Tm[i] = (T[i+1]+T[i])/2.
#
plt.plot(Tm,G)
plt.title("Décélération")
plt.xlabel("t en sec.")
plt.ylabel("$\gamma$ en g");
## END SOLUTION
../../../../_images/b860b156eedd7621282434aba917e6fc2de6502b75a6e5b59269d2fe6bcb9e81.png

3.6. Calcul de trajectoires en 2D#

Les données de la trajectoire étudiée sont dans le fichier trajectoire.txt qui contient 3 colonnes correspondantes au temps (en s.), et aux 2 composantes de la vitesse suivant x et y (en m/s).

bib_validation('cours','MGC2028L')
from Circuit import Circuit,Circuit2,test_vitesse,test_trajectoire,test_acceleration
Circuit("trajectoire.txt",2.,2.);

3.6.1. lecture des données de vitesse#

Dans la cellule suivante:

  • lire les données à partir du fichier en utilisant la fonction loadtxt et les mettre dans les 3 tableaux T,U,V

  • convertir les vitesses en km/h et calculer le module de la vitesse dans Um.

  • déterminer pour cette amplitude, la valeur moyenne Umean, la valeur min Umin et la valeur max Umax en km/h

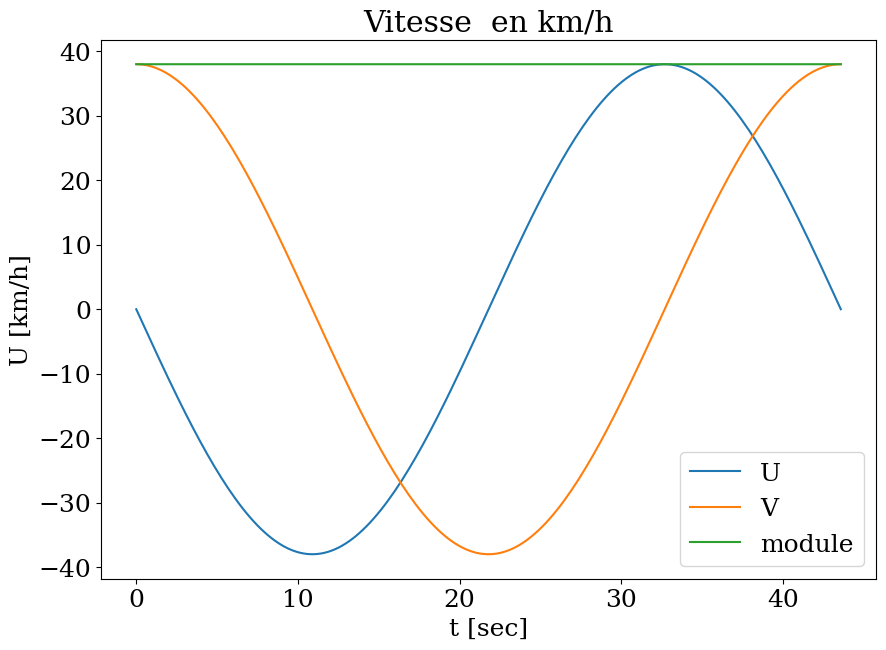
  • tracer les composantes de vitesse et l’amplitude de la vitesse en fonction du temps

T = None
U = None
V = None
Um = None
Umean = None
Vmin  = None
Umax  = None
### BEGIN SOLUTION
T,U,V = np.loadtxt('trajectoire.txt',unpack=True)
U = U*3.600
V = V*3.600
Um = np.sqrt(U**2 + V**2)
Umean = Um.mean()
Umax = Um.max()
Umin = Um.min()
print("Vitesse moyenne={:.1f}km/h min={:.1f} km/h max={:.1f}km/h".format(Umean,Umin,Umax))
# tracer 
plt.figure(figsize=(10,7))
plt.plot(T,U,label="U")
plt.plot(T,V,label="V")
plt.plot(T,Um,label="module")
plt.legend()
plt.xlabel('t [sec]')
plt.ylabel('U [km/h]')
plt.title("Vitesse  en km/h");
#plt.savefig("vitesse.png")
### END SOLUTION

Vitesse moyenne=45.0km/h min=45.0 km/h max=45.0km/h
../../../../_images/cf13c51440cc38e5f1c2bf4563b573a408ad44a42043a5d9b8e4d4abd1eb399b.png 
# test sur les résultats (a executer)
assert((U.size == T.size) and (V.size == T.size))
print("Vitesse moyenne={:.1f}km/h min={:.1f} km/h max={:.1f}km/h".format(Umean,Umin,Umax))
assert(test_vitesse("trajectoire.txt",Umean,Umin,Umax))

Vitesse moyenne=45.0km/h min=45.0 km/h max=45.0km/h

3.6.2. Calcul de la trajectoire#

A partir des composantes de vitesse U et V , calculer la trajectoire en fonction du temps, i.e. la position \(X_i\) et \(Y_i\) pour chacun des temps \(T_i\). Sur chaque intervalle \([T_{i-1},T_i]\), on utilisera la vitesse moyenne pour calculer la position \(X_i\) à l’instant \(T_i\) en fonction de la position précédente \(X_{i-1}\) à \(T_{i-1}\), i.e.

\[ X_{i} \approx X_{i-1} + \bar{U} dt = X_{i-1} + \frac{(U_{i} + U_{i-1})}{2} (T{i}-T_{i-1}) \]

Attention aux unités

Dans la cellule suivante:

  1. calcul la position des points de la trajectoire dans les 2 vecteurs numpy X et Y

  2. en déduire la longueur de la trajectoire dans la variable L

  3. vérifier le calcul par comparaison avec la vitesse moyenne précédente

  4. tracer la trajectoire (X,Y) ainsi que la vitesse sur le même graphe.

  5. Expliquer en quelques lignes comment vous avez vérifié votre calcul

On utilisera la fonction plt.quiver(X,Y,U,V) qui permet de tracer des flèches de longueur U,V aux points X,Y. Pour éviter de tracer trop de flèches, on pourra prendre un point sur 8 en remplaçant X par X[::8] et idem pour les autres arguments.

X = None
Y = None
L = None
### BEGIN SOLUTION
N = T.size
X = np.zeros(N)
Y = np.zeros(N)
# attention T en seconde, U en km/h, position en km
for i in range(1,N):
    X[i] = X[i-1] + 0.5*(U[i]+U[i-1])*(T[i]-T[i-1])/3600
    Y[i] = Y[i-1] + 0.5*(V[i]+V[i-1])*(T[i]-T[i-1])/3600
# calcul longueur
L = 0
for i in range(1,X.size):
    L += np.sqrt((X[i]-X[i-1])**2 + (Y[i]-Y[i-1])**2)
print("Longueur de la trajectoire L={:.2f} km".format(L))
# tracer
plt.figure(figsize=(12,8))
plt.plot(X,Y)
plt.quiver(X[::8],Y[::8],U[::8],V[::8])
plt.title("Trajectoire")
plt.xlabel("X en km")
plt.ylabel("Y en km")
plt.axis('equal');
#plt.savefig("trajectoire.png")
### END SOLUTION

Longueur de la trajectoire L=0.31 km
../../../../_images/6285ee900ab7ab9946d747632de4df96e3c54ae116074f49f2cff9af50a3774b.png

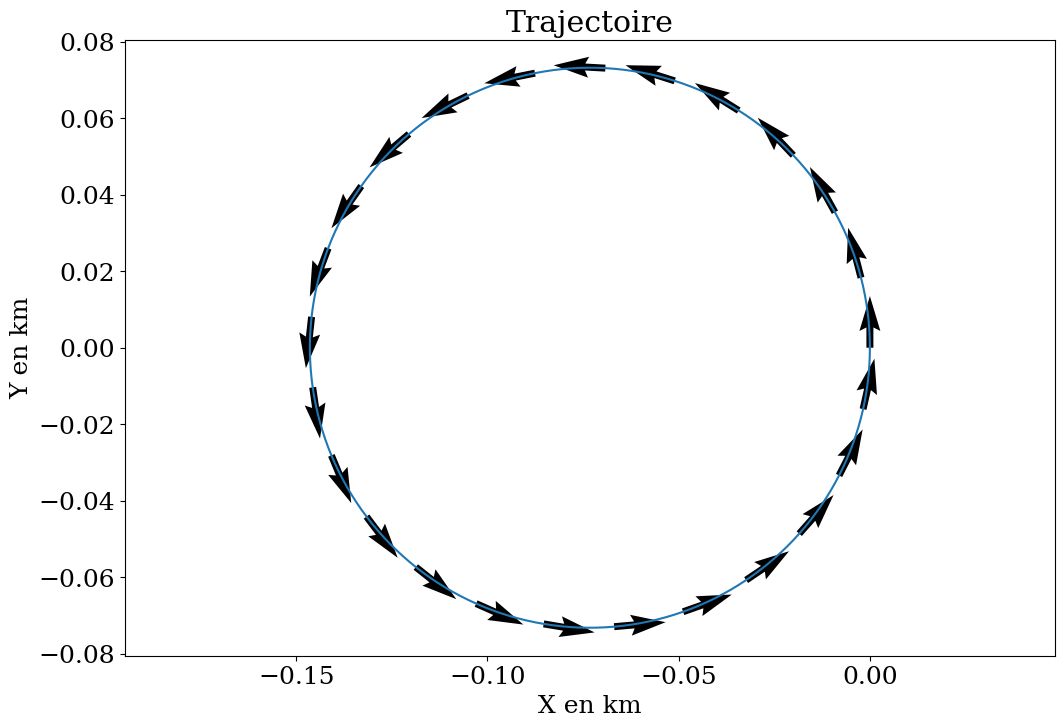
3.6.3. Commentaire sur la courbe#

3.6.4. Calcul de l’accélération#

Calculer l’accélération tangentielle et normale, i.e. le vecteur accélération projeté dans le référentiel local directe formé par la tangente et la normale en chaque point de la trajectoire.

Dans la cellule suivante:

  1. Calculer les composantes suivant x et y de l’accélération sur chacun des segments \([T_{i},T_{i+1}]\) de la trajectoire, en utilisant l’accroissement de vitesse suivant x et suivant y. On mettra le résultat dans les vecteurs numpy Gx et Gy respectivement. On utilisera pour unité le G (i.e. on adimensionne le résultat avec l’accélération de la pesanteur \(g=9.81 m s^{-2}\))

\[ Gx_i = \frac{\Delta U}{\Delta t} = \frac{U_{i+1} - U_{i}}{T_{i+1} - T_{i}}\]

  1. Calculer la composante de l’accélération tangentielle en projetant le résultat suivant la tangente et mettre le résultat dans le vecteur Gt .

  2. Faire de même pour l’accélération normale et mettre le résultat dans le vecteur Gn

  3. Tracer les 2 composantes d’accélérations tangentielles et normales en fonction du temps.

Gx = None
Gy = None
Tx = None
Ty = None
Gt = None
Gn = None
THETA = None
### BEGIN SOLUTION
# normalisation U en km/h et T en sec
g = 9.81
N = X.size
Gx = np.zeros(N-1)
Gy = np.zeros(N-1)
Gn = np.zeros(N-1)
Gt = np.zeros(N-1)
for i in range(0,N-1):
    Gx[i] = ((U[i+1]-U[i])/(T[i+1]-T[i]))/(3.6*g)
    Gy[i] = ((V[i+1]-V[i])/(T[i+1]-T[i]))/(3.6*g)
    # tangente et normale (sens trigo)
    tx = (U[i+1]+U[i])/2
    ty = (V[i+1]+V[i])/2
    tn = np.sqrt(tx**2+ty**2)
    tx = tx / tn
    ty = ty / tn
    Gt[i] =  tx*Gx[i] + ty*Gy[i]
    Gn[i] = -ty*Gx[i] + tx*Gy[i]
#
# calcul du temps au milieu de l'intervalle
Tm = (T[0:N-1]+T[1:N])/2.
# tracer
plt.figure(figsize=(14,8))
plt.plot(Tm,Gn,label="Gn")
plt.plot(Tm,Gt,label='Gt')
plt.xlabel("t [sec]")
plt.ylabel("$\gamma/g$")
plt.legend()
plt.title("Acceleration");
#plt.savefig("acceleration.png")
### END SOLUTION
../../../../_images/becd24acb403b49b4c3c55d8175ab1e0213ce38ec92d8c8082a2857252ab5756.png

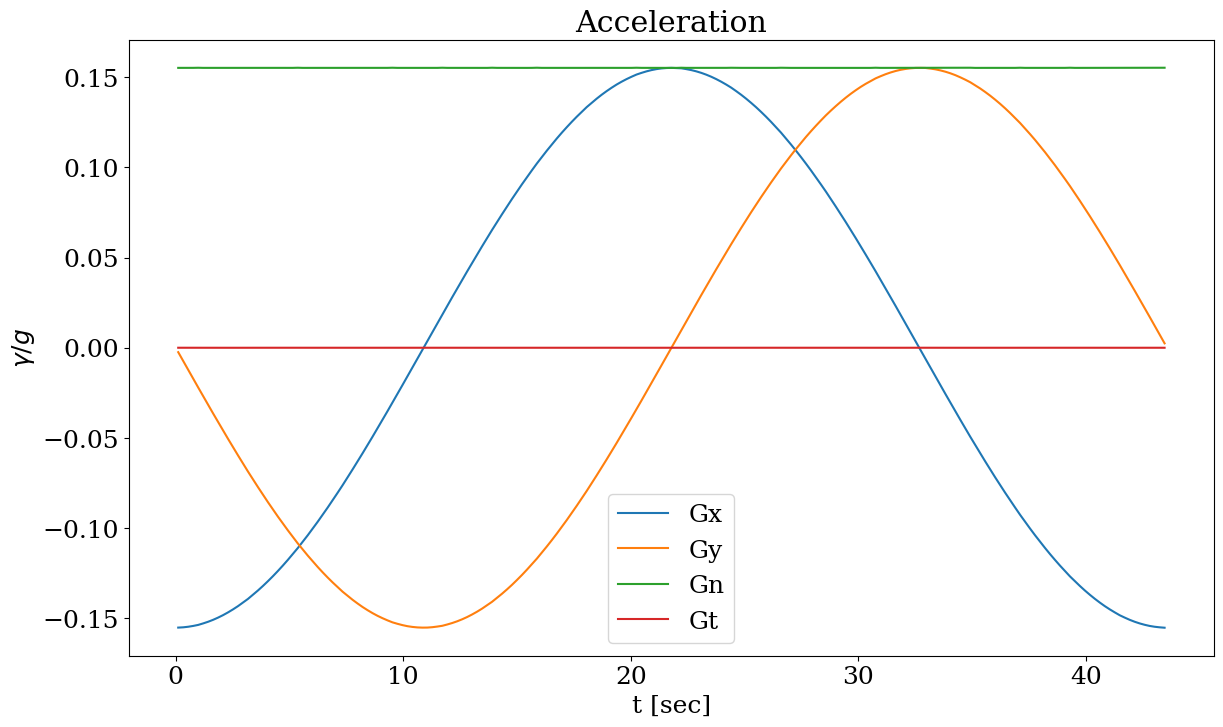
3.6.5. Commentaire sur la courbe#

# test sur les résultats (a executer)
assert((Gx.size == T.size-1) and (Gy.size == T.size-1))
assert((Gn.size == T.size-1) and (Gt.size == T.size-1))
assert(test_acceleration("trajectoire.txt",Gt,Gn,None))

3.7. FIN de la leçon#

Contenu