Tableaux numpy et courbes matplotlib

Contenu

3.2. Tableaux numpy et courbes matplotlib#

Marc BUFFAT, dpt mécanique, Université Lyon 1 et [1]

[1] basé sur le cours « Engineering Computations » du Pr L. Barba (Washington Univ.)

images/numpy_array.png

3.2.1. Introduction#

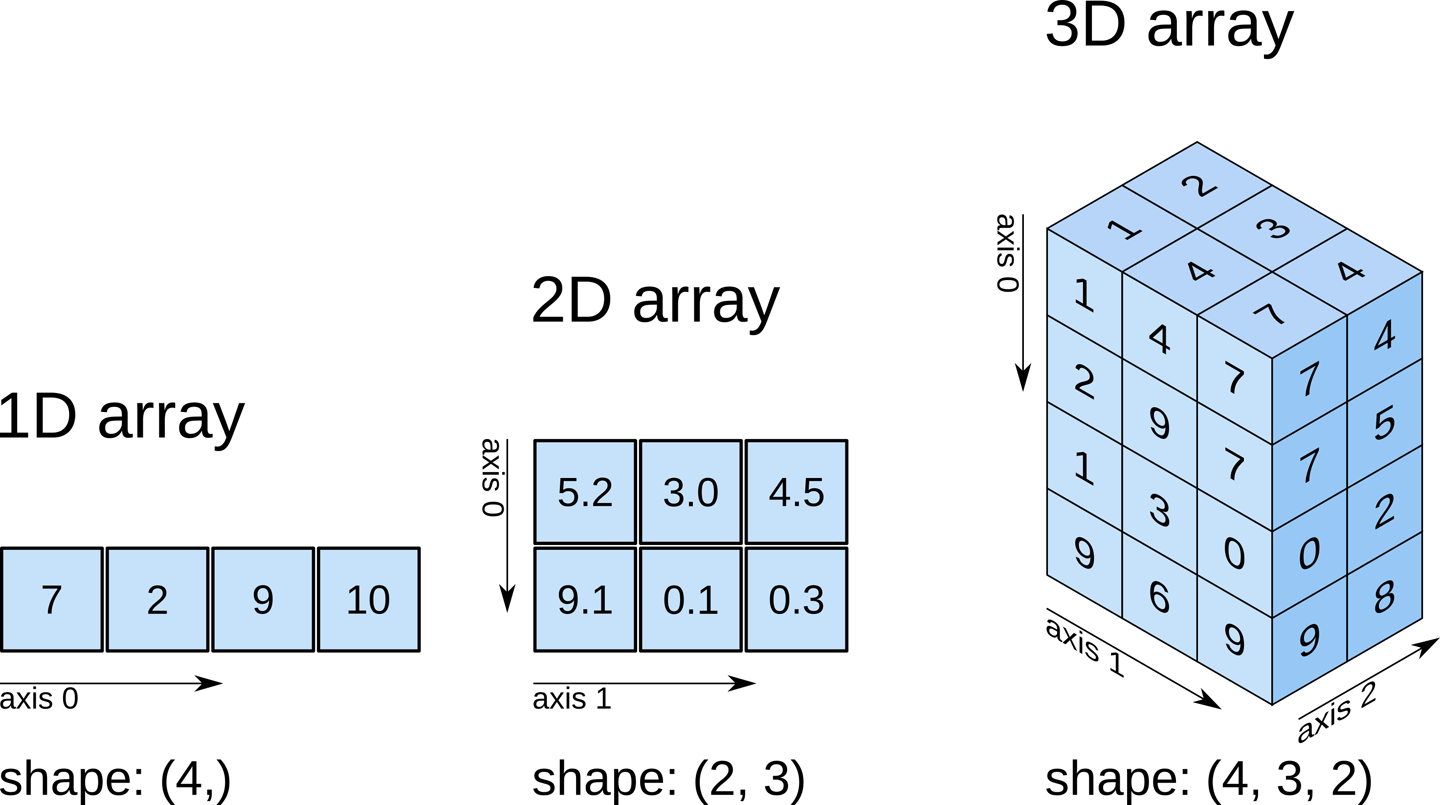
Pour beaucoup d’applications en mécanique, on est amené à manipuler des tableaux qui sont des séquences de données du même type. Ils ressemblent beaucoup aux listes, à l’exception de la contrainte sur le type des éléments. Cela apporte un énorme avantage en termes d’efficacité aux tableaux par rapport aux listes. Ainsi, les méthodes sur les tableaux s’exécutent beaucoup plus rapidement que celles sur les listes.

Grâce aux bibliothèques, le langage Python permet de traiter efficacement des applications numériques en sciences et technologie. Pour le calcul scientifique, la bibliothèque la plus importante est NumPy (Numerical Python), qui fournit les structures de données de tableaux (array) à n dimensions ( ndarray), avec toutes les fonctions, opérations et algorithmes pour les calculs d”algèbre linéaire. Nous utiliserons aussi la bibliothèque Matplotlib pour tracer les données en deux dimensions.

3.2.2. Algorithme de réussite#

pour résoudre un problème avec l’aide d’un ordinateur

Phase d’analyse: réflexion algorithmique avec un papier et un crayon

comprendre ce que l’on doit faire
déterminer comment on va le faire
vérifier sur un cas simple

Phase d’implémentation: programmation

traduire l’algorithme dans un langage de programmation
utilisation de bibliothèque
tenir compte de la syntaxe (erreur de syntaxe simple)
valider l’implémentation à chaque étape

Phase de validation:

sur un cas simple dont on connaît la solution

Phase d’application

traitement du cas

Analyse (critique) du résultat

compte rendu

3.2.2.1. Règles de programmation: Zen du Python#

# zen du python
import this

The Zen of Python, by Tim Peters

Beautiful is better than ugly.
Explicit is better than implicit.
Simple is better than complex.
Complex is better than complicated.
Flat is better than nested.
Sparse is better than dense.
Readability counts.
Special cases aren't special enough to break the rules.
Although practicality beats purity.
Errors should never pass silently.
Unless explicitly silenced.
In the face of ambiguity, refuse the temptation to guess.
There should be one-- and preferably only one --obvious way to do it.
Although that way may not be obvious at first unless you're Dutch.
Now is better than never.
Although never is often better than *right* now.
If the implementation is hard to explain, it's a bad idea.
If the implementation is easy to explain, it may be a good idea.
Namespaces are one honking great idea -- let's do more of those!

3.2.3. Importation de bibliothèques#

En Python, les bibliothèques ne sont pas chargées automatiquement, mais doivent etre importés explicitement en utilisant la commande import. Par exemple, pour importer NumPy, avec toutes ses fonctions d’algèbre linéaire, on utilise

# soit
import numpy
# ou
import numpy as np

La deuxième forme, que nous utiliserons, permet de donner un nom abrégé (ici sp) à la bibliothèque, que l’on utilise à la place du nom de la bibliothèque (i.e. numpy).

Une fois la bibliothéque chargée, on peut utiliser les fonctions de la bibliothèque en ajoutant devant le nom de la bibliothéque ou son nom abrégé. Par exemple, certaines fonctions couramment utilisées avec numpy sont:

Suivez les liens pour voir la documentation de ces fonctions NumPy très utiles, ou utiliser le menu Aide->Numpy Reference!

import numpy as np

3.2.4. Création de tableaux#

Pour créer un tableau NumPy à partir d’une liste existante de valeurs ( homogènes), on utilise numpy.array():

   numpy.array([3, 5, 8, 17])

NumPy propose de nombreuses façons de créer des tableaux.

Par exemple numpy.ones() et numpy.zeros() créent des tableaux remplis de uns et de zéros, respectivement. On passe en argument le nombre souhaité d’éléments du tableau.

Créer dans la cellule suivante un tableau de 1 de dimension 5 et un tableau de 0 de dimension 3.

# écrire votre code ici
### BEGIN SOLUTION
T = np.array([3.,5.,8.,17.])
T = np.ones(4)
T = np.zeros(4)
T = 4.*np.ones(4)
T = np.zeros(4) + 4
print("T=",T)
type(T[0])
### END SOLUTION

T= [4. 4. 4. 4.]

numpy.float64

Une autre fonction numpy.arange() crée un tableau de valeurs régulièrement espacées de pasdans un intervalle définit [debut,fin] mais où finest exclu.

Syntaxe:

numpy.arange(debut, fin, pas)

où debut vaut par défaut zéro,fin est exclus du tableau et pas a une valeur par défaut de 1.

Utiliser les commandes suivantes et analyser le résultat:

np.arange(4)
np.arange(2, 6)
np.arange(2, 6, 2)
np.arange(2, 6, 0.5)

# écrire votre code ici
### BEGIN SOLUTION
X = np.arange(1,5,2)
print(X)
### END SOLUTION

[1 3]

la fonction numpy.linspace() est similaire à numpy.arange(), mais utilise un nombre d’échantillons N au lieu du pas. Il renvoie un tableau de N valeurs avec des nombres régulièrement espacés sur l’intervalle spécifié [debut,fin] où finest inclu.

Syntaxe:

numpy.linspace(debut,fin,N)

Utiliser les commandes suivantes et analyser les résultats:

  np.linspace(2.0, 3.0)
  len(np.linspace(2.0, 3.0))
  np.linspace(2.0, 3.0, 6)
  np.linspace(-1, 1, 9)

# écrire votre code ici
### BEGIN SOLUTION
Y = np.linspace(2.,3.,11)
print(Y)
Y.size
### END SOLUTION

[2.  2.1 2.2 2.3 2.4 2.5 2.6 2.7 2.8 2.9 3. ]

3.2.5. Opérations sur les tableaux#

En affectant un tableau à une variable, on peut ensuite faire simplement des opérations sur le tableau, qui correspondent à des opérations éffectuées sur chaque élément du tableau (i.e. terme à terme).

Utiliser les commandes suivantes et analyser les résultats

   X = np.linspace(-1, 1, 9)
   Y = X * X
   Z = np.sqrt(Y)
   W = X + Z

# écrire votre code ici
### BEGIN SOLUTION
X = np.linspace(-1,1,21)
Y = X*X
Z = np.sqrt(Y)
print("X=",X,"Y=",Y,"Z=",Z)
### END SOLUTION

X= [-1.  -0.9 -0.8 -0.7 -0.6 -0.5 -0.4 -0.3 -0.2 -0.1  0.   0.1  0.2  0.3
4  0.5  0.6  0.7  0.8  0.9  1. ] Y= [1.   0.81 0.64 0.49 0.36 0.25 0.16 0.09 0.04 0.01 0.   0.01 0.04 0.09
16 0.25 0.36 0.49 0.64 0.81 1.  ] Z= [1.  0.9 0.8 0.7 0.6 0.5 0.4 0.3 0.2 0.1 0.  0.1 0.2 0.3 0.4 0.5 0.6 0.7
8 0.9 1. ]

Nous pouvons également diviser des tableaux, mais il faut faire attention à ne pas diviser par zéro. Cette opération se traduira par un nan qui signifie Not a Number. Python effectuera toujours la division, mais nous informera du problème.

Tester le résultat de l’opération

   X / Y

# écrire votre code ici
### BEGIN SOLUTION
X / Y
### END SOLUTION

/tmp/ipykernel_1496606/10227156.py:3: RuntimeWarning: invalid value encountered in divide
  X / Y

array([ -1.        ,  -1.11111111,  -1.25      ,  -1.42857143,
        -1.66666667,  -2.        ,  -2.5       ,  -3.33333333,
        -5.        , -10.        ,          nan,  10.        ,
         5.        ,   3.33333333,   2.5       ,   2.        ,
         1.66666667,   1.42857143,   1.25      ,   1.11111111,
         1.        ])

3.2.6. Tableaux multidimensionnels#

3.2.6.1. tableaux 2D#

NumPy peut créer des tableaux de N dimensions. Par exemple, un tableau 2D ressemble à une matrice et est créé à partir d’une liste imbriquée comme suit:

  A = np.array([[1, 2], [3, 4]])

Les opérations sur matrices sont des opérations terme à terme sur chaque élément.

A partir des 2 matrices A, B suivantes, affichez le résultat de

A + B
A - 2B
A * B

questions

Que se passet-t-il si les matrices ne sont pas de la même dimension ?
Peut on utiliser une notation implicite pour le soperations p.e. 2B ?

A = np.array([[1, 2], [3, 4]])
B = np.array([[1, -1], [0, 1]])
# votre code ici
### BEGIN SOLUTION
print("A=",A[0,1],"B=",B[1])
# calcul
Y = A + B
Z = A * B
print("Y=",Y)
print("Z=",Z)
### END SOLUTION

A= 2 B= [0 1]
Y= [[2 1]
 [3 5]]
Z= [[ 1 -2]
 [ 0  4]]

Attention la dernière opération A*B ne correspond pas à la multiplication matricielle (réfléchissez pourquoi ?)

La multiplication matricielle est obtenue avec l’opérateur @ ou la fonction numpy.dot()

    A @ B
    np.dot(A,B)

Dans la cellule suivante calculer le produit matriciel des 2 matrice A et B.

Si X est le vecteur donné ci dessous, calculer le produit matrice vecteur $A X$

Que fournit l’expression

A*X

X = np.array([1,2])
# votre code ici
### BEGIN SOLUTION
Y = A*X
print("Y=",Y)
Y = A@X
print("Y=",Y)
### END SOLUTION

Y= [[1 4]
 [3 8]]
Y= [ 5 11]

3.2.6.2. algèbre linéaire#

En mécanique, on doit manipuler assez souvent des systèmes d’équations linéaires. Numpy possède une sous-bibliothèque d’algèbre linéaire linalg fournissant les fonctions suivantes pour un système linéaire $$ A X = D $$

np.linalg.det(A) calcule le déterminant de A
np.linalg.inv(A) calcule $A^{-1}$ l’inverse de A
np.linalg.solve(A,D) calcule la solution X du système linéaire $A X = D$
np.linalg.eigvals(A)calcul les valeurs propres de A
np.linalg.eig(A)calcul les valeurs et les vecteurs propres de A

remarque importante

pour résoudre un système linéaire numériquement on n’utilise jamais la méthode mathématique $ X = A^{-1} D$ en calculant $A^{-1}$ l’inverse de A. En effet même si on sait calculer l’inverse de A numériquement avec np.linalg.inv(A), cette méthode est sujette à des erreurs importantes d’arrondie et est inefficace. On utilise à la place la méthode d’élimination de Gauss (que vous verrez dans le cours de méthodes numériques) qui correspond à la fonction np.linalg.solve(A,D).
pensez à consultez la documentation numpy et numpy.linalg (menu Aide->numpy)

exercise En utilisant le vecteur D suivant et la matrice A précédente, calculer la solution Y de $$ A Y = D $$ et mettre le résultat dans la variable Y

Comment peut-on vérifier le résultat ?

D = np.array([5,11/3.])
# votre code ici
### BEGIN SOLUTION
X = np.linalg.solve(A,D)
print("X=",X)
# verification
R = A@X - D
print("R=",R)
### END SOLUTION

X= [-6.33333333  5.66666667]
R= [0.00000000e+00 1.33226763e-15]

3.2.6.3. sélection des éléments d’un tableau#

Pour accéder aux éléments d’une matrice on utilise la notation classique [ligne,colonne].

Pour sélectionner une ligne entière on utilise : à la place de ligne, et idem pour une colonne.

Pour sélectionner une partie du tableau on utilise la notation debut:fin pour afficher les valeurs de debut à fin (attention fin est exclu)

Exercices

afficher la valeur de la première ligne, première colonne de A,
afficher la valeur de la première ligne, deuxième colonne de A,
afficher la première ligne de A,
afficher la seconde colonne de A.

# votre code ici
### BEGIN SOLUTION
A[1],A[1,:],A[:,1]
### END SOLUTION

(array([3, 4]), array([3, 4]), array([2, 4]))

3.2.6.4. boucle sur les éléments d’un tableau#

la bibliothèque numpy possède de nombreuses fonctions pour manipuler des tableaux. par contre dans certain cas on doit effectuer des calculs particuliers qui nécessitent de faire des boucles itératives sur les éléments d’un tableau.

Python offre divers formes de boucles itératives à utiliser suivant les besoins. Nous verrons ici uniquement des boucles sur des tableaux 1D ou vecteurs:

3.2.6.4.1. boucle sur les valeurs#

soit un tableau Tab, on s’intéresse à la valeur val des éléments successifs du tableau? C’est la boucle classique en Python:

   for val in Tab:
      print(val)

exercise on veut déterminer le nombre de valeurs d’un tableau qui sont supérieures à une valeur donnée. Par exemple dans le tableau X suivant, on veut connaître le nombre de valeurs supérieure à 0.5

X = np.random.rand(5)
print(X)
# votre code ici
### BEGIN SOLUTION
compteur = 0
for x in X:
    if x > 0.5 :
        compteur = compteur + 1
print("nbre de valeurs > 0.5 =",compteur)
### END SOLUTION

[0.59530827 0.36303468 0.85888096 0.99015292 0.60981989]
nbre de valeurs > 0.5 = 4

3.2.6.4.2. boucle sur les indices et les valeurs#

Si l’on souhaite modifier les valeurs du tableau, la boucle précédente ne le permet. Il faut avoir accés aussi à l’indice i de la valeur val dans le tableau Tab.

En python la boucle s’écrit alors:

   for i,val in enumerate(Tab):
      print(val,"se trouve a l'indice ",i)

exercise en reprenant l’exemple précédent, on souhaite écrêter le tableau X en remplaçant les valeurs supérieures à 0.5 par 0.5.

# votre code ici
### BEGIN SOLUTION
for i,x in enumerate(X):
    if x > 0.5 :
        X[i] = 0.5
print("X=",X)
### END SOLUTION

X= [0.5        0.36303468 0.5        0.5        0.5       ]

3.2.6.4.3. boucle sur les indices uniquement#

enfin on peut vouloir faire une boucle uniquement sur les indices, dans le cas ou manipule plusieurs tableaux.

En python la boucle s’écrit alors:

   for i in range(len(Tab)):
      print("pour l'indice ",i," la valeur vaut ",Tab[i])

On a besoin de la taille du tableau Tab que l’on peut obtenir par la fonction générique len() ou la méthode .size() pour un tableau ndarray

exercise en reprenant l’exemple précédent, on souhaite écrêter le tableau X en remplaçant les valeurs supérieures à 0.5 par la valeur d’un autre tableau Y de même dimension que X

Y = 0.5*np.random.rand(5)
X = np.random.rand(5)
print("X=",X,"Y=",Y)
# votre code ici
### BEGIN SOLUTION
for i in range(X.size):
    if X[i] > 0.5 :
        X[i] = Y[i]
print("X=",X)
### END SOLUTION

X= [0.93543988 0.88209313 0.94447446 0.72083375 0.84406548] Y= [0.36043875 0.44173871 0.47214951 0.30890776 0.16316407]
X= [0.36043875 0.44173871 0.47214951 0.30890776 0.16316407]

3.2.7. Exercice de programmation#

méthode

description précise du problème posé, de la solution et du test de vérification
écriture de la fonction en python
test de vérification
test de validation (pour la notation)

from validation.validation import check_function,liste_functions
from validation.valide_markdown import test_markdown, test_code, test_algorithme

print("Exercise test: écrire une fonction func t.q.")
nom = "exo51"
!test_exo -e $nom

Exercise test: écrire une fonction func t.q.

Given integers n and k, return a numpy array of length n containing 0 1 2 ... k-1 0 1 2 ... k-1 ...
    

Description de la fonction

la fonction func a 2 arguments : 2 entier n et k et renvoie un tableau X de dimension n contenant
   0,1,2..k-1, 0,1,2 ...
   
par exemple func(5,3) renvoie un tableau X de dimension 5 tq. X=[0,1,2,0,1]

Algorithme func(n,k):
   X = tableau de n zero
   pour i de 0 à n (exclu)
      la valeur est i modulo k 
      X[i] = i % k
   fin pour
   retour X

# test description
assert(test_algorithme('Numpy-Matplotlib.ipynb','cell-algo',minm=20))

#rentrer votre code pour func
### BEGIN SOLUTION
def func(n,k):
    X = np.zeros(n)
    for i in range(n):
        X[i] = i % k
    return X
### END SOLUTION

print("Verification: appel de la fonction")
### BEGIN SOLUTION
print("test:",func(5,3))
### END SOLUTION

Verification: appel de la fonction
test: [0. 1. 2. 0. 1.]

assert(test_code('Numpy-Matplotlib.ipynb','cell-verif','func'))
assert(check_function(func,nom))

validation:  exo51 
Given integers n and k, return a numpy array of length n containing 0 1 2 ... k-1 0 1 2 ... k-1 ...
    

3.2.8. Tracé avec matplotlib#

Pour tracer des courbes, nous utiliserons la bibliothèque matplotlib et son module pyplot. Sous Jupyter on utilise les instructions suivantes:

  %matplotlib inline
  import matplotlib.pyplot as plt

pour utiliser cette librairie avec le nom raccourci plt. La première instruction permet d’afficher les courbes dans le notebook (inline) plutôt que dans une fenêtre à part.

exemple

pour $x\in[0,2]$, on veut tracer les courbes $y_1=x^2$, $y_2=x^3$ et $y_3=\sqrt{x}$. Pour cela on crée un tableau X de valeurs entre 0 et 2, et on calcule ensuite les valeurs des courbes, puis on trace les 3 courbes avec des commandes du type

  plt.plot(X,Y1)

%matplotlib inline
import matplotlib.pyplot as plt
# utilisation de taille de caracatère plus grande
plt.rc('font', family='serif', size='16')

X  = np.linspace(0,2,41)
Y1 = X*X
Y2 = X**3
Y3 = np.sqrt(X)

3.2.8.1. tracé basique#

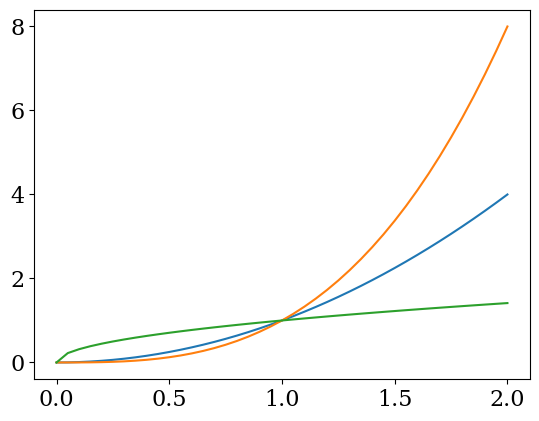
faire un tracé basique des 3 courbes dans la cellule suivante.

Attention ce genre de tracé n’est à utiliser que pour des tests et pas pour présenter des résultats, car les courbes n’ont pas de titre, les axes pas de label. Il faut regarder le code pour éventuellement comprendre.

N’utilisez jamais ce tracé basique pour présenter vos résultats !!!

# tracer basique
### BEGIN SOLUTION
plt.plot(X,Y1)
plt.plot(X,Y2)
plt.plot(X,Y3)
### END SOLUTION

[<matplotlib.lines.Line2D at 0x7f4aadeed8d0>]

../../../../_images/aece09b76b0e91128dc9d82318c62a8f8b329897cb8f8b5fbc619309f744f4e3.png

3.2.8.2. tracé de résultats#

Pour avoir un résultat de qualité, il faut ajouter un titre lisible, des labels sur les axes et sur les courbes:

plt.title
plt.xlabel, plt.ylabel
plt.legend
plt.subplot
plt.figure

# tracer avec des titres et des labels
# tracer d'une figure plus grande
plt.figure(figsize=(10,6))
# plot x^2
plt.plot(X, Y1, color='r', linestyle='-', label='$x^2$')
# plot x^3
plt.plot(X, Y2, color='g', linestyle='--', label='$x^3$')
# plot sqrt(x)
plt.plot(X, Y3, color='b', linestyle=':',  label='$\sqrt{x}$')
# ajoute un titre et des labels 
plt.title('Courbes étudiées')
plt.xlabel('x')
plt.ylabel('y=f(x)')
# ajoute la legende au meilleur endroit
plt.legend(loc='best');

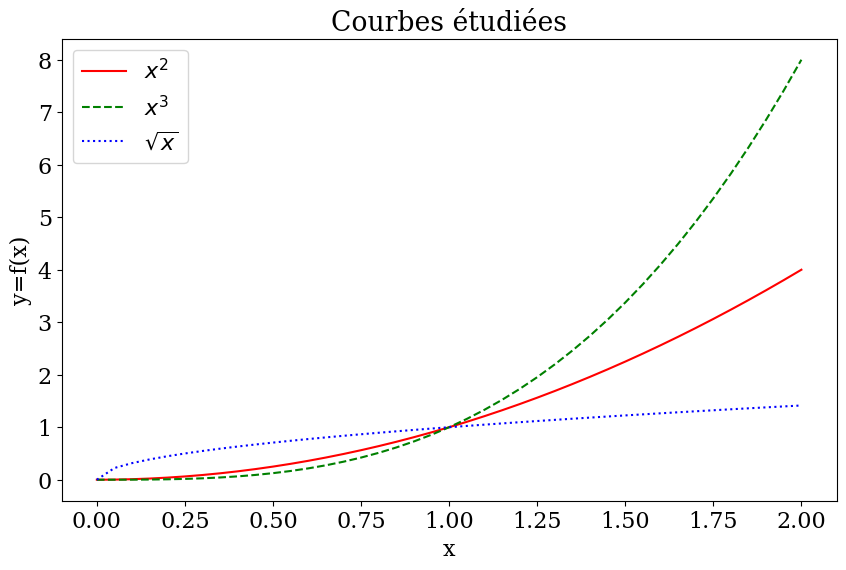
../../../../_images/e11461819940d8797f2aad6f1668d79ca9d7664729bb211dab50a930f9faa1cc.png

On a utiliser une notation $\LaTeX$ pour afficher des expressions mathématiques: $x^2$ pour afficher $x^2$ ou $\sqrt{x}$ pour afficher $\sqrt{x}$.

Consulter le site de matplotlib https://matplotlib.org pour avoir un aperçu des immenses possibilités de tracé de matplotlib.

from IPython.display import IFrame
IFrame('https://matplotlib.org/cheatsheets/_images/handout-beginner.png',width=800,height=500)

IFrame('https://matplotlib.org/cheatsheets/_images/handout-intermediate.png',width=800,height=500)

3.2.9. Exemple 1: étude de fonction#

On veut étudier une fonction $f(x)$ sur un intervalle $[a,b]$, par ex:

\[ f(x) = x \cos 2x \cos 3x \mbox{ sur } [0,7] \]

pour déterminer son maximum

3.2.9.1. Algorithme#

on écrit une fonction f(x) pour calculer la valeur de $x \cos 2x \cos 3x$ en fonction de x
avec cette fonction on calcule la valeur en 50 points équi-répartis sur l’intervalle $[0,7]$
on stocke le résultat dans 2 tableaux numpy: X pour les valeurs de x, et ̀Y pour les valeurs de la fonction
on trace la courbe
on calcule une valeur approchée de la dérivée en chacun des points $x_i=X[i]$ du tableau X en utilisant une approximation par différences centrées, i.e.

\[ f'(x_i) \approx \frac{f(x_{i+1}) - f(x_{i-1})}{x_{i+1}-x_{i-1}} \]

attention pour le premier et le dernier point, la formule doit être adaptée !

\[f'(x_0) \approx \frac{f(x_{1}) - f(x_{0})}{x_{1}-x_{0}} \mbox{ et } f'(x_n) \approx \frac{f(x_{n}) - f(x_{n-1})}{x_{n}-x_{n-1}} \]

on écrit le résultat dans un tableau numpy noté DY
on trace la courbe de la dérivée
on détermine la position du maximum de la courbe sur l’intervalle d’étude de façon précise en utilisant la dérivée.

En notant que le maximum de cette courbe est le dernier maximum local à la position $x_{max}$, i.e. qui vérifie:

\[ f'(x_{max}) = 0 \mbox{ avec } f'(x_{max}-\epsilon) > 0 \mbox{ et } f'(x_{max}+\epsilon) <0 \]

Pour cela on détermine les 2 derniers points consécutifs (k,k+1) de DYtels que : DY[k]>0 et DY[k+1]<0

La valeur de $x_{max}$ est alors l’intersection du segment (X[k],DY[k]) à (X[k+1],DY[k+1]) avec l’axe des x

On mettra la valeur de $x_{max}$ dans la variable xmax et la valeur de $f(x_{max})$ dans fmax

3.2.9.2. Programmation Python#

# code Python calcule et trace fonction 
### BEGIN SOLUTION
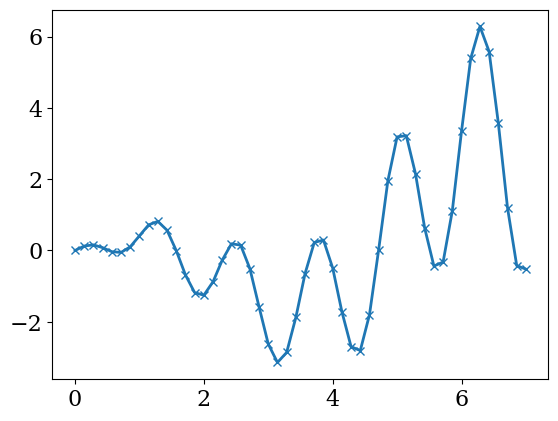
f = lambda x:x*np.cos(2*x)*np.cos(3*x)
X = np.linspace(0,7,50)
Y = f(X)
plt.plot(X,Y,'x-',lw=2)
### END SOLUTION

[<matplotlib.lines.Line2D at 0x7f4aad90c2b0>]

../../../../_images/feb07ab6589334eedee54b567992a2e611973ebd59972ea594f3bac30172bdaf.png

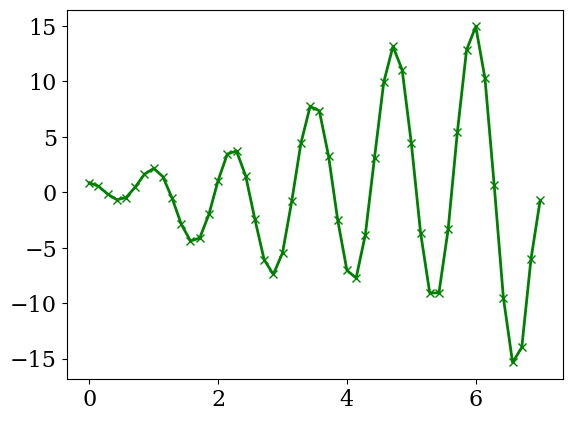
# code Python calcul et trace dérivée
### BEGIN SOLUTION
DY = np.zeros(X.size)
for i in range(1,X.size-1):
    DY[i] = (Y[i+1]-Y[i-1])/(X[i+1]-X[i-1])
DY[0] = (Y[1]-Y[0])/(X[1]-X[0])
DY[-1]= (Y[-1]-Y[-2])/(X[-1]-X[-2])
plt.plot(X,DY,'-xg',lw=2)
### END SOLUTION

[<matplotlib.lines.Line2D at 0x7f4aad947ee0>]

../../../../_images/38179fae36dde20e176dedfc3db3883cd1463377ed6c8e1e1a84cf05a00c3771.png

# calcul du maximum
### BEGIN SOLUTION
k = X.size-1
# selectionne intervalle ou f' est < 0
while DY[k] > 0: k=k-1
# recherche changement de signe
while DY[k] < 0: k=k-1
xmax = X[k] - DY[k]*(X[k+1]-X[k])/(DY[k+1]-DY[k])
fmax = f(xmax)
print(" maximun en x={} f(x)={} (max={} en {})".format(xmax,fmax,np.max(Y),X[np.argmax(Y)]))
### END SOLUTION

 maximun en x=6.295301350047519 f(x)=6.289296204140849 (max=6.28545297771401 en 6.285714285714286)

3.2.10. Exemple 2: calcul de racine#

Soit la courbe cubique $y=P(x)$ avec

\[ P(x) = 4x^3 - 2x \]

Pour une valeur de $R$ donnée, on cherche à déterminer la valeur de $x$ telle que $P(x)=R$, c.a.d la racine de l’équation $P(x)=R$, i.e. $$ \mbox{Trouvez }x\in\mathcal{R} \mbox{ t.q. } P(x)=R $$

Attention: ce problème peut admettre une ou plusieurs solutions.

3.2.10.1. Analyse du problème#

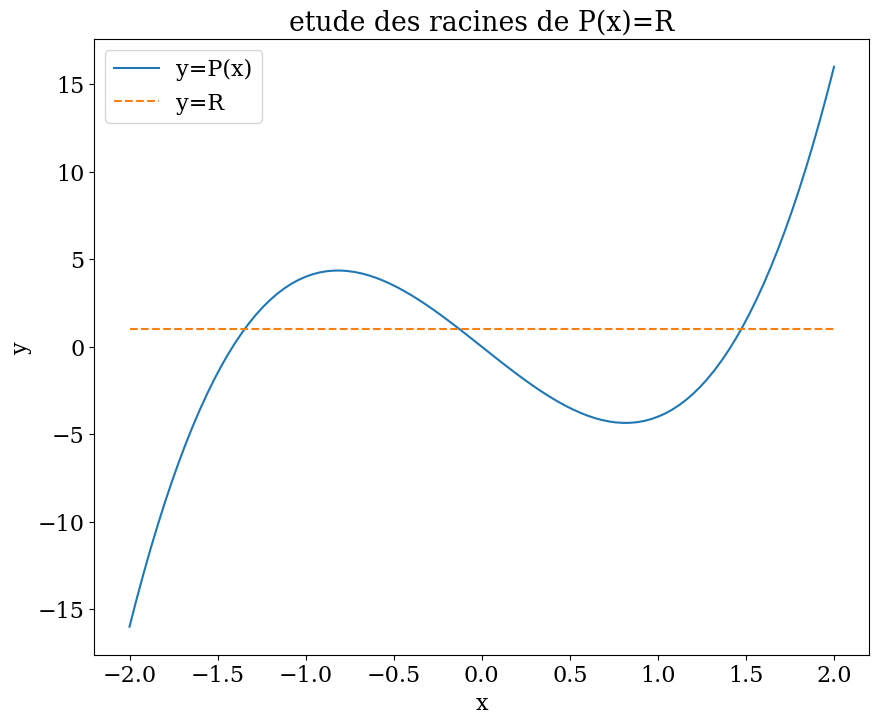
Géométriquement, le problème revient à déterminer l’intersection de la courbe $y=P(x)$ avec la droite horizontale $y=R$.

On trace donc la courbe $y=P(x)$ et la droite $y=R$ pour $R=1.0$

On calcule ensuite la valeur de la racine avec la fonction fsolve de la bibliothèque numpy.optimize.

Attention on doit choisir une point de départ proche de la racine que l’on souhaite calculer !

# tracer
### BEGIN SOLUTION
R = 1.0
P = lambda x: 4*x*(x**2-2)
X = np.linspace(-2,2,101)
plt.figure(figsize=(10,8))
plt.plot(X,P(X),label='y=P(x)')
plt.plot([X[0],X[-1]],[R,R],'--',label='y=R')
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title("etude des racines de P(x)=R");
### END SOLUTION

../../../../_images/ba4e2d7036e027cb1026aba20786351b046b7812f47ab6b10d25b20b943f6d3d.png

3.2.10.2. calcul de la solution suivant R#

on utilise fsolve pour résoudre l’équation et on vérifie en partant de 0

Que se passe-t-il si on part de -1, -0.9, ou -0.8?

from scipy.optimize import fsolve
### BEGIN SOLUTION
F = lambda x : P(x)-R
x0 = fsolve(F,0.)[0]
#x0 = fsolve(F,-0.8)[0]
print("solution :",x0)
print("erreur   :",P(x0)-R)
### END SOLUTION

solution : -0.1260001925862561
erreur   : -1.1102230246251565e-16

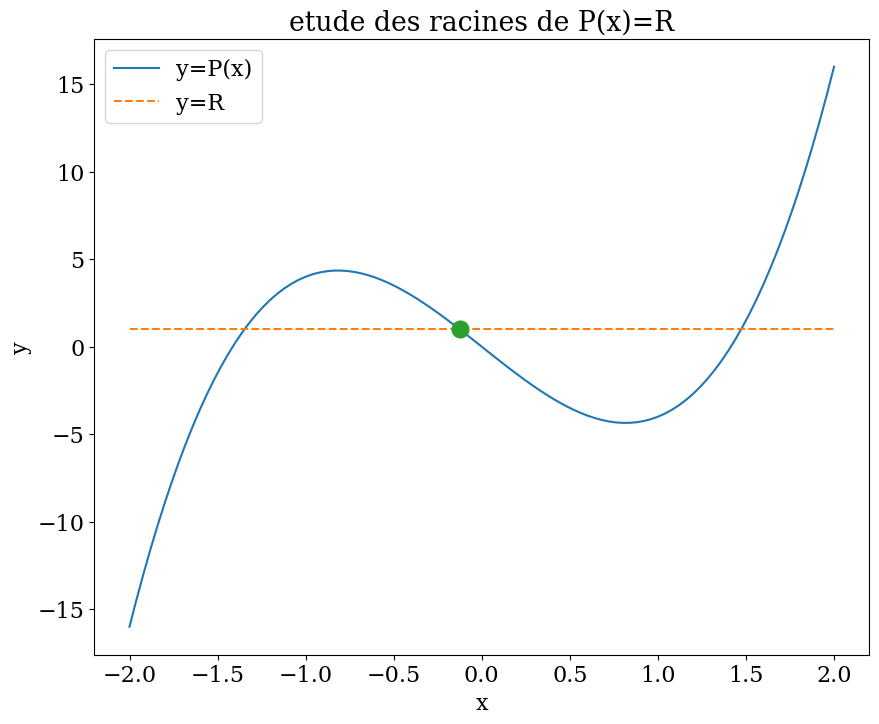
# verification graphique
### BEGIN SOLUTION
plt.figure(figsize=(10,8))
plt.plot(X,P(X),label='y=P(x)')
plt.plot([X[0],X[-1]],[R,R],'--',label='y=R')
plt.plot([x0],[P(x0)],'o',markersize=12)
plt.legend()
plt.xlabel('x')
plt.ylabel('y')
plt.title("etude des racines de P(x)=R");
### END SOLUTION

../../../../_images/cc45003d08bfb8587ac43806accb67aabbceb862920ebf5e0eeca6b577c027ba.png

3.2.11. Bibliographie#

Python. The official Python web site.
Python tutorials. Le tutoriel officiel Python.
Think Python. “”How to Think Like a Computer Scientist”” by Allen B. Downey (free book).
Scientific Python Le site officiel de SciPy, qui regroupe les bibliothèques scientifiques les plus utilisées en Python: numpy, scipy, matplotlib, sympy et pandas