2.9. Exercices Python#
Petits exercices Python sur le tracé avec matplotlib
Marc Buffat, Dpt Mécanique Lyon 1
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from validation.valide_markdown import test_markdown, test_code
from validation.validation import info_etudiant, bib_validation
from IPython.display import display, Markdown, clear_output
bib_validation("cours","MGC2028L")
from SolutionExo import solution2
---------------------------------------------------------------------------
ModuleNotFoundError Traceback (most recent call last)
Cell In[1], line 10
8 from IPython.display import display, Markdown, clear_output
9 bib_validation("cours","MGC2028L")
---> 10 from SolutionExo import solution2
ModuleNotFoundError: No module named 'SolutionExo'
# nom etudiant
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if NUMERO_ETUDIANT is None:
NOM,PRENOM,NUMERO_ETUDIANT = info_etudiant()
notebook_name="Exercises3.ipynb"
printmd("## Etudiant {} {} id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
np.random.seed(NUMERO_ETUDIANT)
_X = np.array([-np.round(np.random.rand(),2),np.random.randint(5),np.random.randint(10)])
2.9.1. Tracé d’une courbe: exo 1#
Pour tracer une courbe \(y=f(x)\) avec matplotlib, il faut définir les valeurs de x à utiliser dans un tableau numpy X, puis calculer les valeurs de f(x) correspondantes et les mettre dans un tableau Y.
On utilise ensuite les fonction matplotlib : plot() xlabel() ylabel() title()
legend() pour tracer les courbes avec un titre, des labels pour les axes et des légendes.
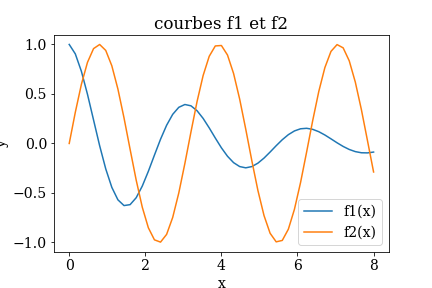
Tracer de cette façon les 2 courbes \(f_1(x)=e^{\alpha x}\cos{\omega x}\) et \(f_2(x)=\sin{\omega x}\) sur l’intervalle \([0,L]\) en prenant N=51 points équi-répartis.
Les valeurs à utiliser sont affichées ci-dessous.
Vous devez obtenir une courbe de ce type:
printmd(f"**valeurs à utiliser $\\alpha$={_X[0]} $\omega$={_X[1]} L={_X[2]}**")
import numpy as np
import matplotlib.pyplot as plt
X = None
Y1,Y2 = None,None
### BEGIN SOLUTION
### END SOLUTION
2.9.2. Tracé d’une trajectoire : exo 2#
Pour tracer la trajectoire d’un objet en 2D, on donne ses coordonnées X et Y à différents instants T. Pour étudier la trajectoire sur un intervalle de temps \([0,T_f]\), on choisit N=101 points équi-répartis pour créer un vecteur T. On calcule ensuite la position en x et y à chacun de ces instants T.
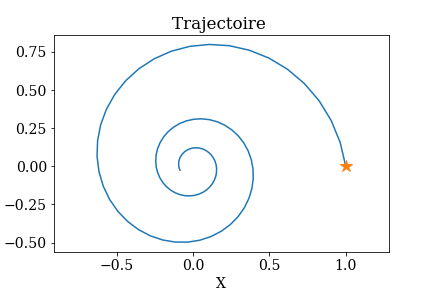
Tracer la trajectoire correspondant à \(x(t)=e^{\alpha t}\cos{\omega t}\) et \(y(t)=e^{\alpha t}\sin{\omega t}\)
avec un titre, des lables sur les axes et en utilisant la fonction plt.axis('equal') pour avoir des axes avec le même rapport d’aspect. On indiquera la position initiale
en utilisant la fonction plot pour tracer un symbole
en un point (x0,y0): plt.plot([x0],[y0],"*",markersize=12)
Vous devez obtenir une courbe de ce type:
printmd(f"**valeurs à utiliser $\\alpha$={_X[0]} $\omega$={_X[1]} $T_f$={_X[2]}**")
T = None
X,Y = None,None
### BEGIN SOLUTION
### END SOLUTION
2.9.3. Tracé d’une trajectoire avec la vitesse : exo 3#
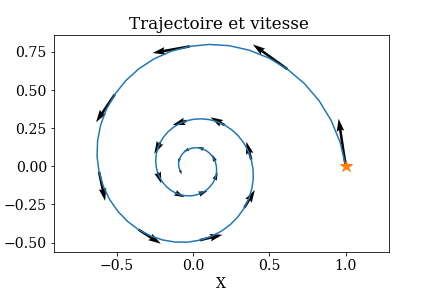
Reprendre l’exercice précédent avec les mêmes données, auquel on rajoute le tracé des vecteurs vitesses.
Pour ajouter le tracé de la vitesse, on utilise la fonction `plt.quiver(X,Y,U,V) où U et V sont les composantes de la vitesse. Pour alléger le tracé, on ne prendra qu’un point sur 5.
Pour déterminer U et V, on calculera la dérivée \(\dot{x}(t)\) et \(\dot{x}(t)\)
Vous devez obtenir une courbe de ce type:
T = None
X,Y = None,None
U,V = None,None
### BEGIN SOLUTION
### END SOLUTION