8. EDO: système masse ressort avec amortissement

Marc BUFFAT, dpt mécanique, Université Lyon 1

inspiré par le cours « Engineering Computations » du Pr L. Barba (Washington Univ.)

# bibliothéque
%matplotlib inline
import numpy as np
from matplotlib import pyplot as plt
plt.rc('font', family='serif', size='14')
# parametres
from validation.validation import info_etudiant, bib_validation, test_function
from validation.valide_markdown import test_markdown, test_code
from IPython.display import display, Markdown, clear_output
bib_validation('cours','MGC2028L')
from Oscillation import test1,test2,test3,test4,test5,test6
notebook_name = "TP_vibration.ipynb"
def printmd(string):
    display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
if type(NUMERO_ETUDIANT) is not int :
    NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_  = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Etudiant** {} {}  id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
# parametres
_mcl_ = ['énergie','cinétique','potentielle','période','erreur','amortie','oscillation', 'forcage']
_omega0 = np.random.randint(1,10)
# systeme
_m  = np.round(0.1+2*np.random.rand(),2)
_k  = _m*_omega0**2
_b  = np.round(0.1+0.5*np.random.rand(),2)
# CI
_x0 = np.round(0.5*(2*np.random.rand()-1),2)
_v0 = 0.
# forcage
_omega  = _omega0/2.
_A = np.round(_x0*_omega0**2*0.25*(0.1+np.random.rand()),2)
if (np.abs(_A)<0.5): _A = 0.5
#
printmd("**parametres:** masse m={}, raid.k={}, amort.b={} Forcage: omega={},A={} CdtsInit: x0={},v0={}".format(_m,_k,_b,_omega,_A,_x0, _v0))

Etudiant Marc BUFFAT id=137764122

parametres: masse m=1.66, raid.k=26.56, amort.b=0.47 Forcage: omega=2.0,A=-1.08 CdtsInit: x0=-0.28,v0=0.0

8.1. Le système masse-ressort

Le système oscillant mécanique le plus simple est une masse \( m \) attachée à un ressort, sans frottement. Nous avons discuté de ce système dans la leçon précédente. En général, cependant, ces systèmes sont soumis à des frottements représentés par un amortisseur mécanique et à une force motrice d’excitation. De plus, la force de rappel du ressort pourrait être une fonction non linéaire de la position.

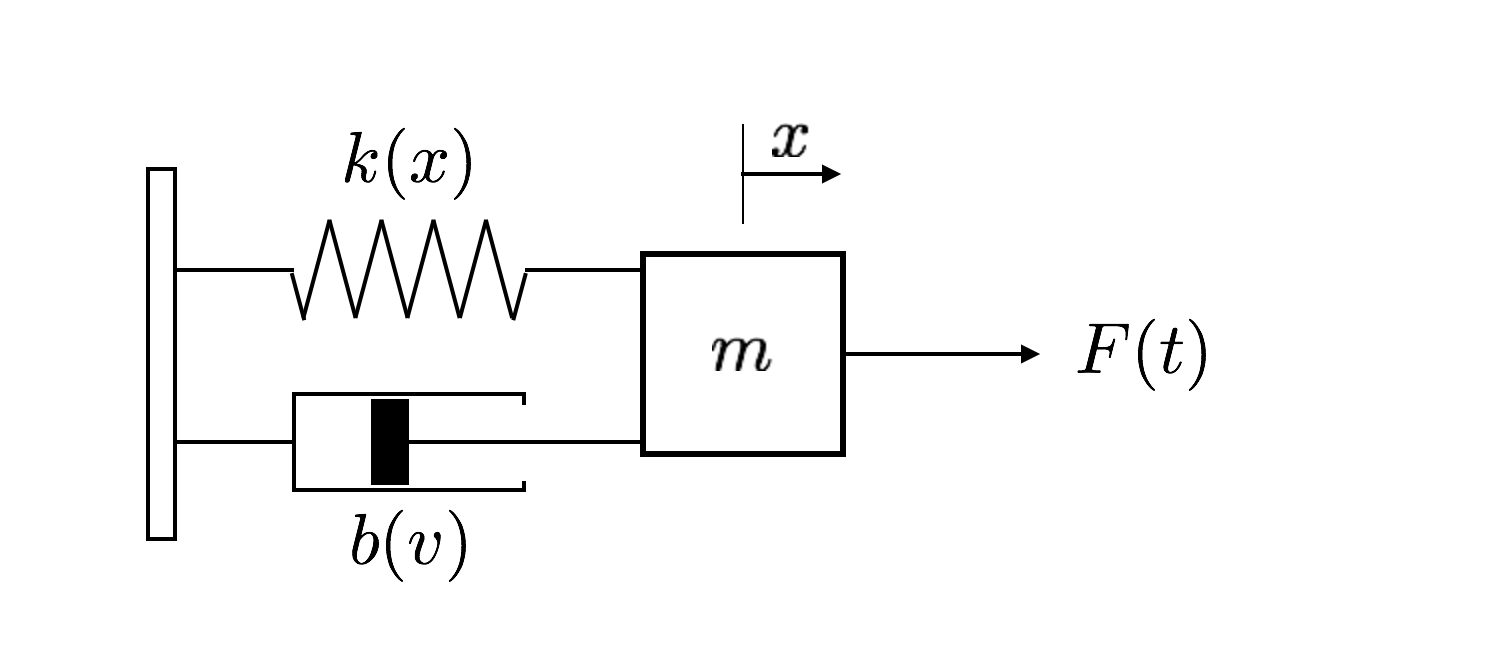
8.1.1. système masse ressort avec amortissement et forçage

La loi de Newton appliquée au système masse-ressort général (entraîné, amorti) s’écrit:

(8.1)\[\begin{equation} \mbox{Trouvez x(t) tq. : } m \ddot{x} = m\,f(t) -mb\,\dot{x} - k\,x \end{equation}\]

où

• \(x(t)\) représente l’allongement du ressort

• \(f(t)\) représente une force extérieure de forçage par unité de masse,

• \(b\dot{x}\) une force d’amortissement par unité de masse,

• \(k\,x(t)\) une force de rappel .

En divisant par \(m\) et en notant \(\omega^2 = \frac{k}{m}\), ce système est équivalent à

• Trouver x(t) t.q. :

(8.2)\[\begin{equation} \ddot{x} = f(t) -b\,\dot{x} - \omega_0^2\,x \end{equation}\]

que l’on peut l’écrire comme un système de deux équations différentielles (2) d’ordre 1,

• Trouver x(t),v(t) t.q.:

(8.3)\[\begin{eqnarray} \dot{x} &=& v, \\ \dot{v} &=& f(t) - \omega_0^2 x - bv \end{eqnarray}\]

En notant \(Y(t)\) le vecteur d’état

(8.4)\[\begin{equation} \mathbf{Y} = \begin{bmatrix} x \\ v \end{bmatrix} \end{equation}\]

la forme vectorielle du système précédent s’écrit alors:

(8.5)\[\begin{equation} \dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y},t) \mbox{ avec } \mathbf{F}(\mathbf{Y},t) = \begin{bmatrix} v \\ f(t) - \omega_0^2\,x - b\,v \end{bmatrix}. \end{equation}\]

Dans ce système général, la variable temps apparaître explicitement dans le second membre de droite, via la fonction de forçage \(f(t)\), donc le second membre \(F\) dépend explicitement de \(Y(t)\) et de \(t\).

8.2. Méthode numérique

Pour calculer la solution numérique du système d’EDO

\[\dot{\mathbf{Y}} = \mathbf{F}(\mathbf{Y}(t),t)\]

on utilise la méthode de Runge Kutta, mais sous forme matricielle puisque la solution est un vecteur (de dimension 2) et non plus un scalaire.

Pour cela on se fixe le temps de simulation \(t_{max}\) et le nombre de temps \(N\), ce qui permet de définir un vecteur T contenant les \(N\) temps où on calcule numériquement la solution, et qui est donnée par :

\[ T_i = i\Delta t \mbox{ pour } i=0,N-1 \]

On calcule ensuite la solution numérique sous forme d’une matrice Y de dimension \((N,2)\) qui pour chaque ligne i contient la valeur numérique de \(\mathbf{Y}(T_i)\) au temps \(T_i\)

• Pour i=0,

la condition initiale fournit la première valeur de \(\mathbf{Y}\)

\[Y[0,:] = \mathbf{Y}_0\]

• Pour i de 1 à N-1

on calcule itérativement la valeur de ce vecteur solution \(Y[i,:]\approx \mathbf{Y}(t=T[i])\) avec la méthode numérique de Runge Kutta 2, qui s’écrit sous forme matricielle (en notant \(t_m = \frac{t_i + t_{i-1}}{2}\))

(8.6)\[\begin{align} \mathbf{Y}_m & = \mathbf{Y}[i-1,:] + \frac{\Delta t}{2} \mathbf{F}(\mathbf{Y}[i-1,:],t_{i-1}) \\ \mathbf{Y}[i,:] & = \mathbf{Y}[i-1,:] + \Delta t \,\, \mathbf{F}(\mathbf{Y}_m,t_m). \end{align}\]

8.2.1. Implémentation

Pour appliquer cette méthode, on écrit une fonction F(y,t), qui calcule le second membre de l’EDO avec les valeurs du modèle. Attention yest un vecteur numpy de dimension 2 (contenant la valeur de x et v à l’instant t) et la fonction F(y,t)renvoie un vecteur numpy de dimension 2 contenant les seconds membres du système d’EDO (2).

Il faut ensuite écrire une fonction RK2(F,T,Y0) qui prend pour arguments les paramètres du problème :

1. la fonction second membre F de l’EDO,

2. le vecteur T numpy des pas en temps où on veut calculer la solution

3. la condition initiale Y0 (vecteur dimension 2).

Cette fonction calcule la valeur numérique Ysol de la solution (qui est une matrice). Dans cette fonction :

1. on crée la matrice solution Ysol

2. on initialise la première ligne de Ysol avec Y0

3. en utilisant une boucle itérative, on calcule chaque ligne de Ysol en utilisant la méthode précédente.

4. à la fin, la fonction renvoie cette matrice Ysol, qui contient la solution numérique aux instants T.

8.3. Etude analytique cas sans forcage \(f(t)=0\)

En notant \(b=2\lambda_0\), on obtiens la forme générique de l’équation

Equation du mouvement

\[ \ddot{x} + 2\lambda_0 \dot{x} + \omega_0^2 x = 0 \]

import sympy as sp
from sympy import Derivative, Eq, dsolve
t = sp.symbols('t')
y = sp.symbols('y',cls=sp.Function)
lambda0, omega0 = sp.symbols("lambda_0 omega_0")
eq0 = Derivative(y(t),t,t) + 2*lambda0*Derivative(y(t),t) + omega0**2*y(t)
display("EDO ",eq0)

'EDO '

\[\displaystyle 2 \lambda_{0} \frac{d}{d t} y{\left(t \right)} + \omega_{0}^{2} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)}\]

8.3.1. différents mouvements possibles suivant \(\lambda_0\) (pour \(\omega_0=1\))

équation caractéristique du 2nd degré

\[ x^2 + 2\lambda_0 x + \omega_0^2 = 0\]

• fonction du signe de \(\Delta = \lambda_0^2 - \omega_0^2\)

  • racines imaginaire pures

  • racines complexes

  • racines doubles

  • racines réelles

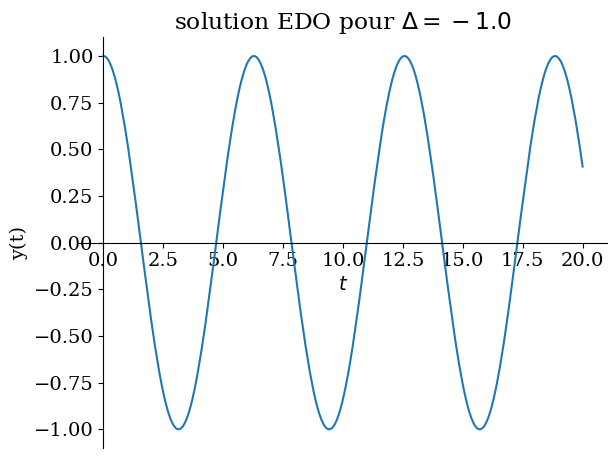
# cas sans amortissement: 
Valnum={lambda0:0,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
sp.plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'

\[\displaystyle y{\left(t \right)} = \cos{\left(t \right)}\]

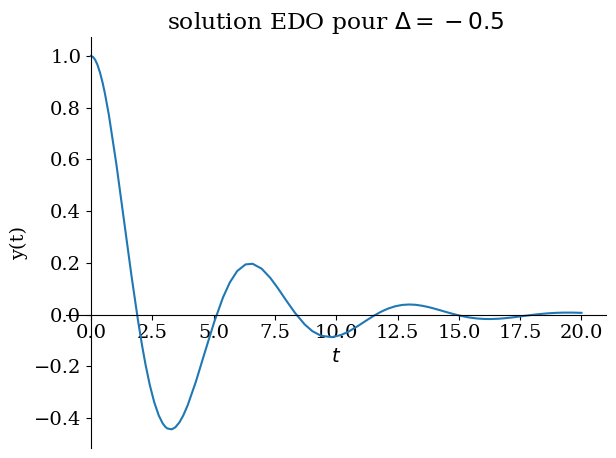
# pseudo periodique amortie
Valnum={lambda0:1/sp.S(4),omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
sp.plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'

\[\displaystyle y{\left(t \right)} = \left(\frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{15} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}}\]

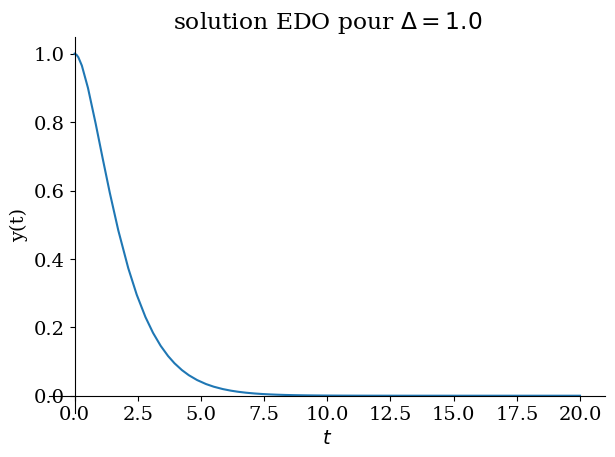
# critique
Valnum={lambda0:1,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
sp.plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'

\[\displaystyle y{\left(t \right)} = \left(t + 1\right) e^{- t}\]

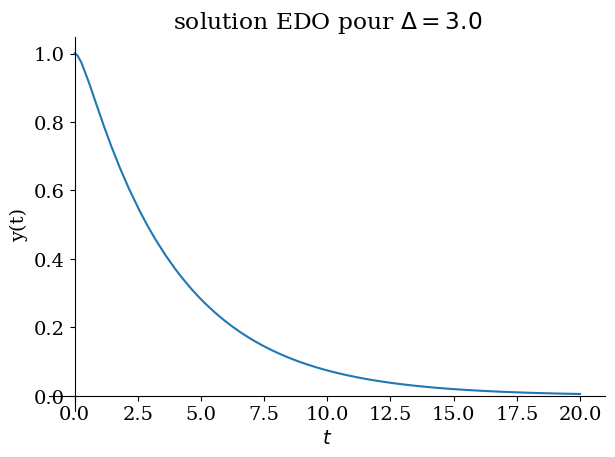
# amortie
Valnum={lambda0:2,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
sp.plot(sol.rhs,(t,0,20),title="solution EDO pour $\Delta ={}$".format(Delta),ylabel="y(t)");

'solution :'

\[\displaystyle y{\left(t \right)} = \left(\frac{1}{2} + \frac{\sqrt{3}}{3}\right) e^{t \left(-2 + \sqrt{3}\right)} + \left(\frac{1}{2} - \frac{\sqrt{3}}{3}\right) e^{- t \left(\sqrt{3} + 2\right)}\]

8.4. Etude analytique: cas avec forçage \(f(t)\) mais sans amortissement

\[ \ddot{y} + \omega_0^2 y = f(t)\]

• solution = solution équation homogène + solution particulière

• si forçage harmonique \(f(t)= A \cos(\omega_1 t)\)

• la solution dépend de la valeur de \(\omega_1\) par rapport à \(\omega_0\)

  • si \(\omega_1 \neq \omega_0\) solution particulière \( y(t) = \alpha \cos{\omega_1 t}\)

  • si \(\omega_1 = \omega_0\) résonnance: solution particulière \( y(t) = t \sin{\omega_0 t}\)

omega1, A = sp.symbols("omega_1 A")
eq1 = Eq(Derivative(y(t),t,t) + omega0**2*y(t),A*sp.cos(omega1*t))
display("EDO ",eq1)

'EDO '

\[\displaystyle \omega_{0}^{2} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = A \cos{\left(\omega_{1} t \right)}\]

8.4.1. différents mouvements possibles fonctions de \(\omega_1\)

On fixe \(\omega_0=1\)

• étude fct de \(\omega_1\)

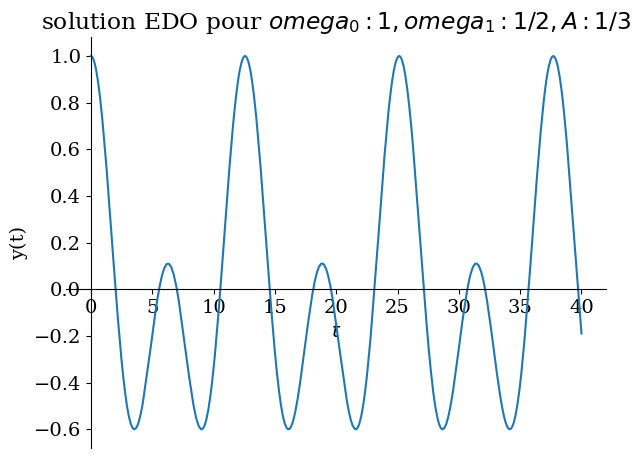
# avec forcage < omega
Valnum={omega0:1,omega1:1/sp.S(2),A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
sp.plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{4 \cos{\left(\frac{t}{2} \right)}}{9} + \frac{5 \cos{\left(t \right)}}{9}\]

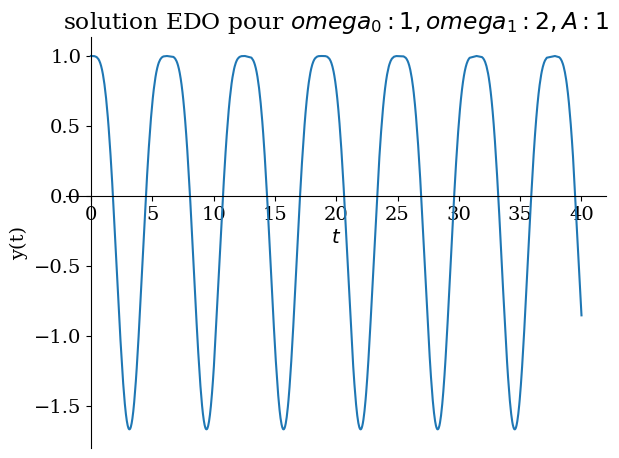
# avec forcage > omega
Valnum={omega0:1,omega1:sp.S(2),A:1}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
sp.plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{4 \cos{\left(t \right)}}{3} - \frac{\cos{\left(2 t \right)}}{3}\]

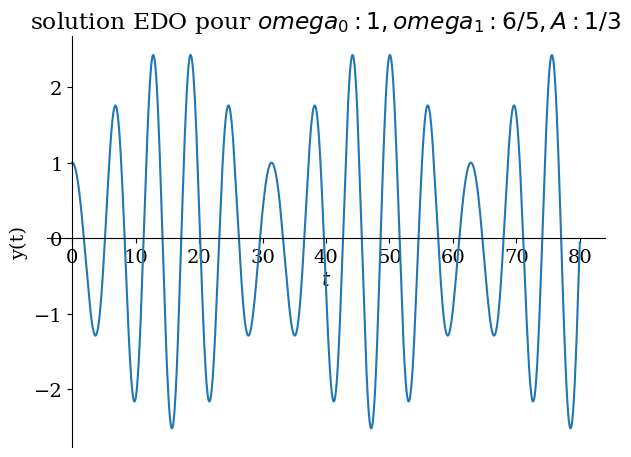
# avec forcage proche de omeg0
Valnum={omega0:1,omega1:6/sp.S(5),A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
sp.plot(sol.rhs,(t,0,80),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{58 \cos{\left(t \right)}}{33} - \frac{25 \cos{\left(\frac{6 t}{5} \right)}}{33}\]

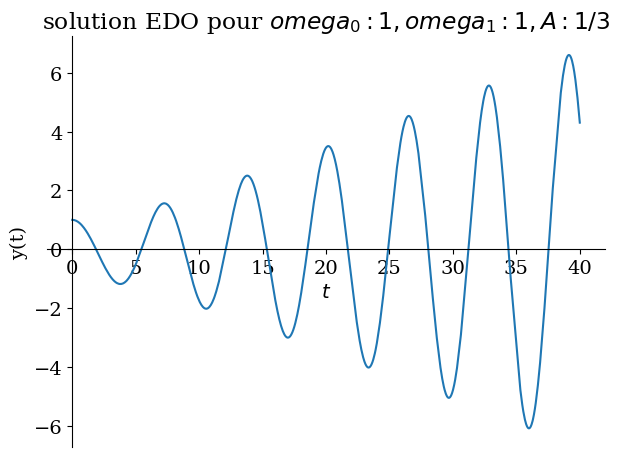
# resonnance omega1=omega0
Valnum={omega0:1,omega1:1,A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
sp.plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{t \sin{\left(t \right)}}{6} + \cos{\left(t \right)}\]

8.4.2. cas avec forçage \(f(t)\) et amortissement

\[ \ddot{y} + 2\lambda_0 \dot{y} + \omega_0^2 y = f(t)\]

• solution = solution équation homogène + solution particulière

omega1, A = sp.symbols("omega_1 A")
eq = Eq(Derivative(y(t),t,t) + 2*lambda0*Derivative(y(t),t) + omega0**2*y(t),A*sp.cos(omega1*t))
display("EDO ",eq)

'EDO '

\[\displaystyle 2 \lambda_{0} \frac{d}{d t} y{\left(t \right)} + \omega_{0}^{2} y{\left(t \right)} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = A \cos{\left(\omega_{1} t \right)}\]

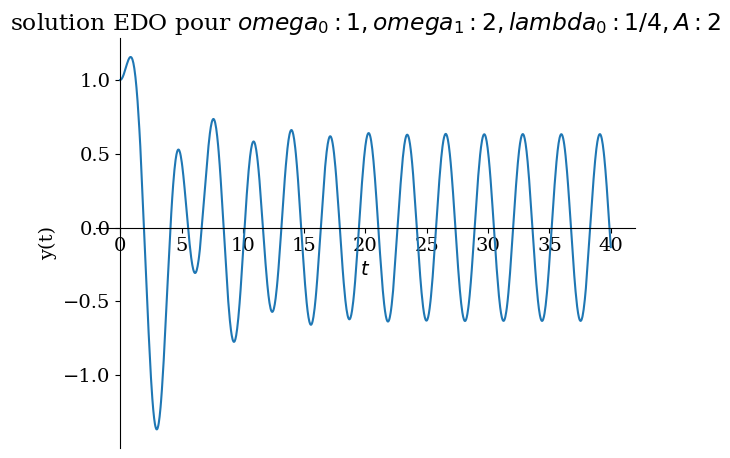
# hors résonance
Valnum={omega0:1,omega1:4/sp.S(2),lambda0:1/sp.S(4),A:2}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
sp.plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = 2 \cos{\left(2 t \right)}\]

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{\sin{\left(2 t \right)}}{5} - \frac{3 \cos{\left(2 t \right)}}{5} + \frac{8 e^{- \frac{t}{4}} \cos{\left(\frac{\sqrt{15} t}{4} \right)}}{5}\]

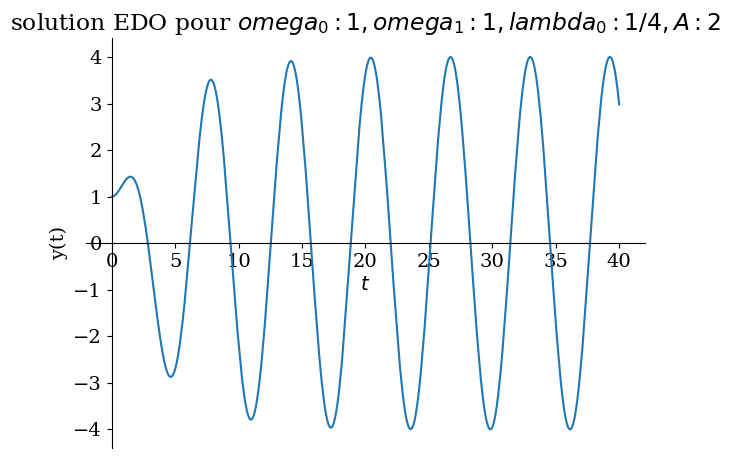
# resonnance
Valnum={omega0:1,omega1:2/sp.S(2),lambda0:1/sp.S(4),A:2}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
sp.plot(sol.rhs,(t,0,40),title="solution EDO pour ${}$".format(Valnum),ylabel="y(t)");

\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = 2 \cos{\left(t \right)}\]

'solution: '

\[\displaystyle y{\left(t \right)} = \left(- \sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}} + 4 \sin{\left(t \right)}\]

8.5. Analyse du mouvement dans l’espace des phases

Le système masse-ressort peut se comporter de différentes manières. Si le ressort est linéaire et qu’il n’y a pas d’amortissement ou de forçage , le mouvement est périodique. Si nous ajoutons de l’amortissement, le mouvement oscillatoire décroît avec le temps. Avec le forçage, le mouvement peut être un peu plus compliqué et parfois présenter une résonance.

Chacun de ces types de mouvement est représenté par des solutions correspondantes au système différentiel, dictées par les paramètres du modèle et les conditions initiales.

Comment avoir une idée de tous les types de solutions à un système différentiel? Une méthode puissante pour ce faire est d’utiliser le plan de phase.

Un système de deux équations différentielles du premier ordre:

\[\begin{split} \mathbf{Y} = \mathbf{F}(Y,t) \mbox{ soit } \begin{eqnarray} \dot{y_1}(t) &=& f_1(y_1, y_2) \\ \dot{y_2}(t) &=& f_2(y_1, y_2) \end{eqnarray} \end{split}\]

avec un vecteur d’état

(8.7)\[\begin{equation} \mathbf{Y(t)} = \begin{bmatrix} y_1(t) \\ y_2(t) \end{bmatrix}, \end{equation}\]

est appelé un système autonome planaire: planaire, car le vecteur d’état a deux composantes; et autonome (auto-génératrice), car la variable de temps n’apparaît pas explicitement sur le côté droit (qui ne s’appliquerait pas au système masse-ressort entraîné).

Pour les conditions initiales données \(\mathbf{Y}(0)=Y_0\), le système a une solution unique. Cette solution peut être représentée par une courbe plane sur le plan 𝑥𝑦 le plan de phase et est appelée une trajectoire du système. C’est une courbe paramétrique fonction de t.

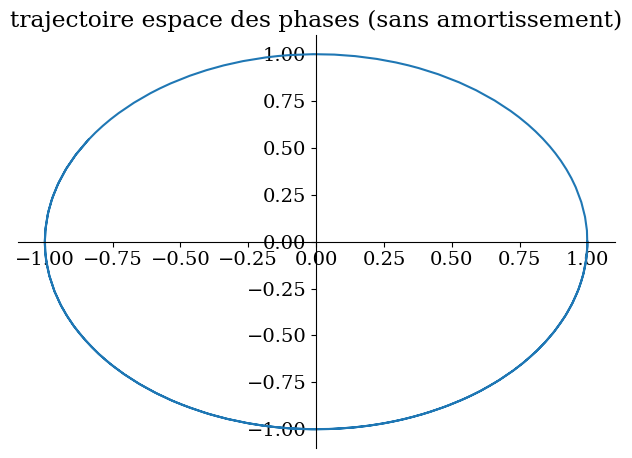
8.5.1. cas sans forcage

# cas sans amortissement: 
Valnum={lambda0:0,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution:",sol)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,10),title="trajectoire espace des phases (sans amortissement)");

'solution:'

\[\displaystyle y{\left(t \right)} = \cos{\left(t \right)}\]

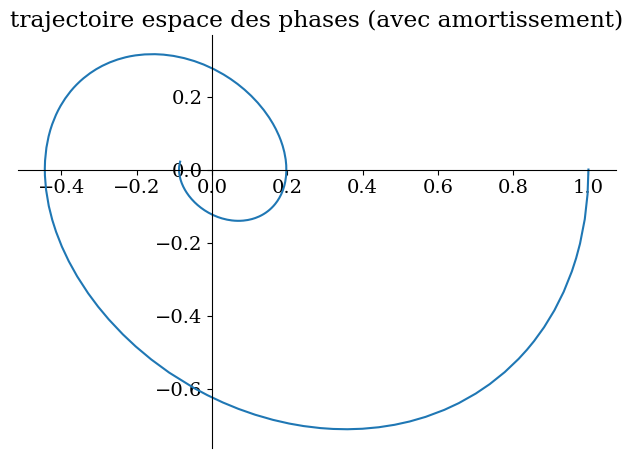
Valnum={lambda0:1/sp.S(4),omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,10),title="trajectoire espace des phases (avec amortissement)");

'solution :'

\[\displaystyle y{\left(t \right)} = \left(\frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{15} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}}\]

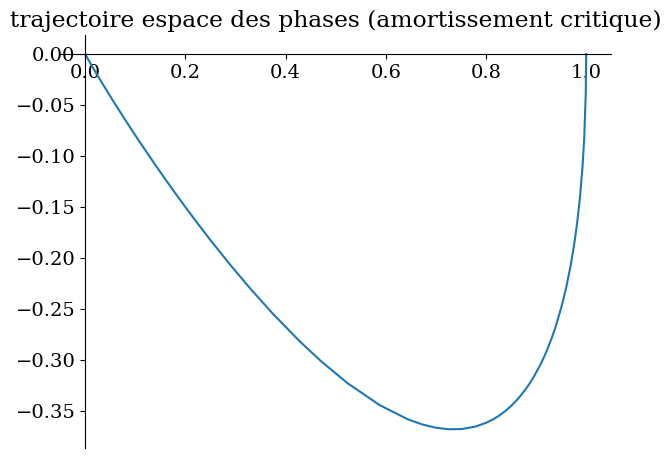
# critique
Valnum={lambda0:1,omega0:1}
Delta = float((lambda0*2-omega0**2).subs(Valnum))
CI={y(0):1,Derivative(y(t),t).subs(t,0):0}
sol = dsolve(eq0.subs(Valnum),ics=CI)
display("solution :",sol)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,10),title="trajectoire espace des phases (amortissement critique)");

'solution :'

\[\displaystyle y{\left(t \right)} = \left(t + 1\right) e^{- t}\]

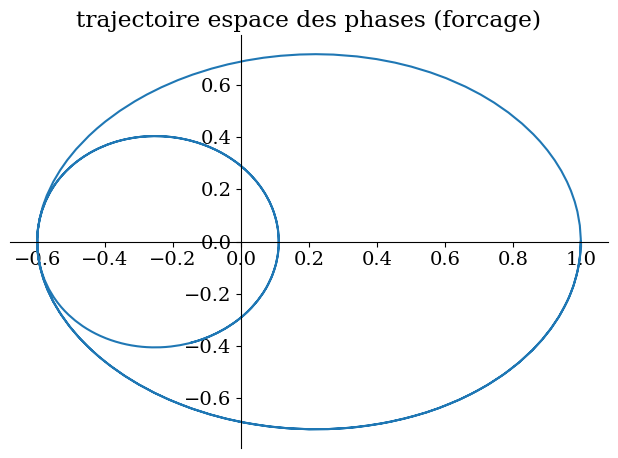
8.5.2. cas avec forcage (sans amortissement)

# avec forcage < omega
Valnum={omega0:1,omega1:1/sp.S(2),A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,20),title="trajectoire espace des phases (forcage)")

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{4 \cos{\left(\frac{t}{2} \right)}}{9} + \frac{5 \cos{\left(t \right)}}{9}\]

<sympy.plotting.plot.Plot at 0x7f787f7e69e0>

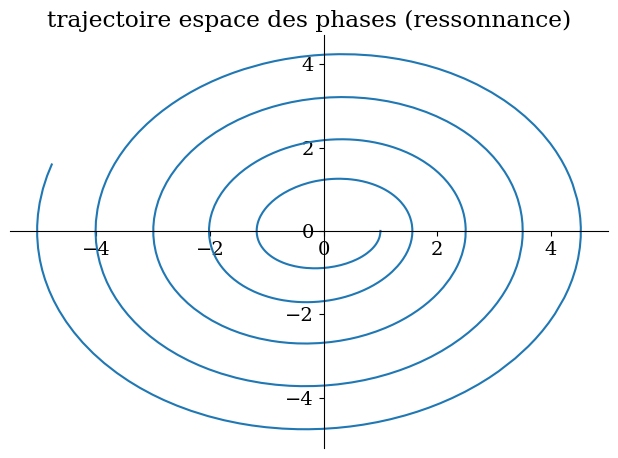
# resonnance omega1=omega0
Valnum={omega0:1,omega1:1,A:1/sp.S(3)}
#
sol = dsolve(eq1.subs(Valnum),ics=CI)
display("solution: ",sol)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,30),title="trajectoire espace des phases (ressonnance)");

'solution: '

\[\displaystyle y{\left(t \right)} = \frac{t \sin{\left(t \right)}}{6} + \cos{\left(t \right)}\]

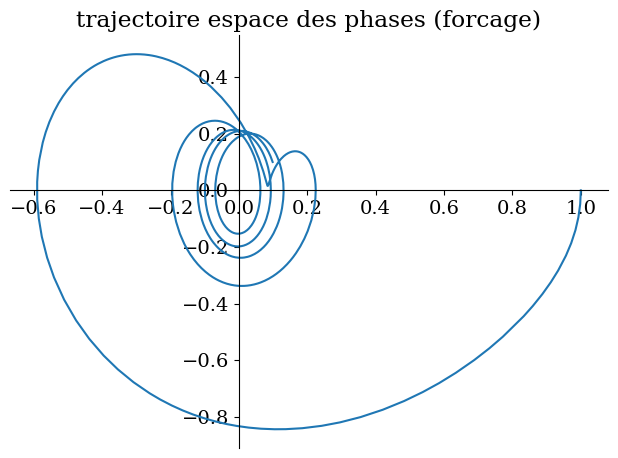
8.5.3. cas général

# 
Valnum={omega0:1,omega1:4/sp.S(2),lambda0:1/sp.S(4),A:1/sp.S(3)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,20),title="trajectoire espace des phases (forcage)");

\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \frac{\cos{\left(2 t \right)}}{3}\]

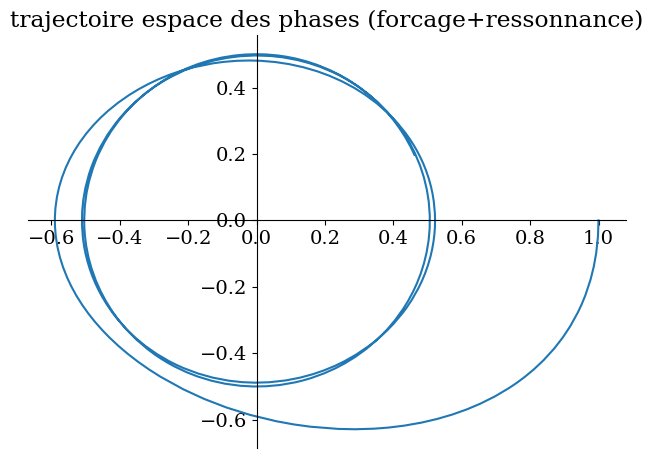
# resonnance
Valnum={omega0:1,omega1:2/sp.S(2),lambda0:1/sp.S(4),A:1/sp.S(4)}
display(eq.subs(Valnum))
#
sol = dsolve(eq.subs(Valnum),ics=CI)
display("solution: ",sol)
y1 = sol.rhs
y2 = y1.diff(t)
sp.plot_parametric((y1,y2),(t,0,20),title="trajectoire espace des phases (forcage+ressonnance)");

\[\displaystyle y{\left(t \right)} + \frac{\frac{d}{d t} y{\left(t \right)}}{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)} = \frac{\cos{\left(t \right)}}{4}\]

'solution: '

\[\displaystyle y{\left(t \right)} = \left(- \frac{\sqrt{15} \sin{\left(\frac{\sqrt{15} t}{4} \right)}}{15} + \cos{\left(\frac{\sqrt{15} t}{4} \right)}\right) e^{- \frac{t}{4}} + \frac{\sin{\left(t \right)}}{2}\]