Modélisation du pendule de Foucault avec sympy et numpy¶

Marc BUFFAT, dpt mécanique, Université Lyon 1

Table des matières

1 Objectifs
- 1.1 calcul symbolique sous Python
- 1.2 Expérience de 1851 au Pantheon
2 Modélisation du pendule de Foucault
3 Mouvement du pendule dans R1
- 3.1 Equations du mouvement dans R1
- 3.2 3 équations
4 Propriétés du système d'équation
5 Prise en compte de la rotation de la terre
6 Résolution numérique
7 ANNEXE 1: solution Analytique
8 ANNEXE 2: étude numérique du mvt 3D du pendule

Objectifs¶

Utilisation d'un outil de calcul formel et de calcul numérique pour étudier la cinématique et la dynamique du pendule, permettant de résoudre complètement le problème.

mise en équation en utilisant du calcul formel pour faciliter les calculs analytiques (changement de repère, projection, composition des mouvements,..)
résolution numérique des équations pour obtenir la solution

ATTENTION ces outils ne sont pas une boite noir pour résoudre automatiquement les problèmes. Il faut comprendre la démarche pour pouvoir les utiliser à bon escient.
introduction au calcul formel
application à la modélisation du pendule sphérique
modélisation et simulation du pendule de Foucault
analyse des résultats

calcul symbolique sous Python¶

sympy symbolic python
vector bibliothèque sympy pour manipuler des vecteurs et des repères en 3D (projection, dérivation ..)
classical mechanics bibliothèque sympy pour l'étude de la cinématique et dynamique des solides
```
import sympy as sp
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.vector import dot
```
Attention en général quand on utilise une fonction d'une bibliothéque python, on préfixe en général la fonction par le nom (simplifié) de la bibliothéque
```
np.cos(..)
sp.symbols(..)
```
Remarque il faut faire attention à ne pas mélanger calcul symbolique et calcul numérique, en particulier pour les fonctions mathématiques:
- sp.sin représente la fonction mathématique (symbolique) sinus. On calcul exactement sa dérivée ou son intégrale, mais on ne peut pas calculer sin(1)!
- np.sin représente la fonction numérique, qui calcule les valeurs numériques approchées de la fonction sinus, p.e. sin(1)

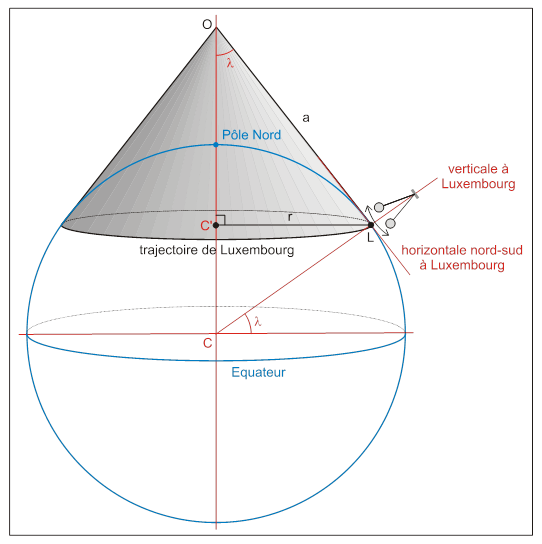
Expérience de 1851 au Pantheon¶

Un pendule de Foucault, du nom du physicien français Jean Bernard Léon Foucault, est une expérience conçue en 1851 pour démontrer la rotation de la Terre par rapport à un référentiel galiléen ainsi que l'existence de la force de Coriolis dans un référentiel non galiléen défini naturellement, à l'endroit où il se trouve, par un observateur terrestre.

Le pendule installé sous la voute du panthéon pesse 25 kg et long de 67m et l'expérience montre une précession de son plan d'oscillation d'environ 32h, due à la rotation de la terre. Voir les références ci-dessous pour des explications sans équation:

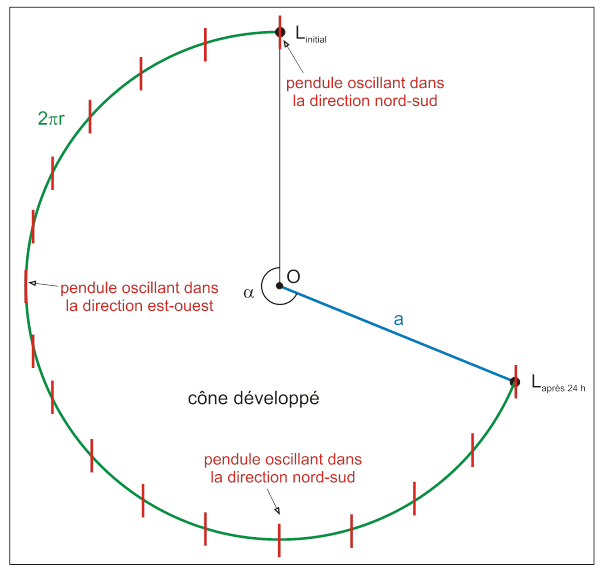Pendule de Foucault: comment montre-t-il que la Terre tourne ?

Les mouvements du pendule de Foucault sont portés par un cône ayant comme cercle de base la trajectoire du lieu où il se trouve, et comme demi-angle au-sommet la latitude de ce lieu. Le pendule oscille dans un plan vertical (à cause de l’attraction terrestre) et dans un référentiel fixe galiléen rien n'oblige le pendule à changer sa direction d’oscillation sur cette surface. Par conséquent, en vertu de l'inertie de la masse du pendule, la direction d'oscillation sur cette figure ne change pas au cours du temps. L’observateur (point L) voit, en revanche, le pendule pivoter au cours du temps par rapport à lui dans le sens horaire.

Modélisation du pendule de Foucault¶

Pour simuler le mouvement du pendule, on modélise

le référentiel du laboratoire $R_1$ par rapport à un référentiel Galiléen $R_0$,
puis le pendule dans le repère du laboratoire $R_1$.

On importe les bibliothèques utilisées dans la suite

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from IPython.core.display import HTML
from IPython.display import display,Image

# bibliothéque de calcul symbolique
import sympy as sp
from sympy.physics.vector import init_vprinting
init_vprinting(use_latex='mathjax', pretty_print=False)
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame, Particle

repère du laboratoire¶

Paramêtres:

R rayon terre
$\Psi_l$: angle de lattitude (49 degré Paris, 46 degré Lyon)
$\Omega$: rotation de la terre

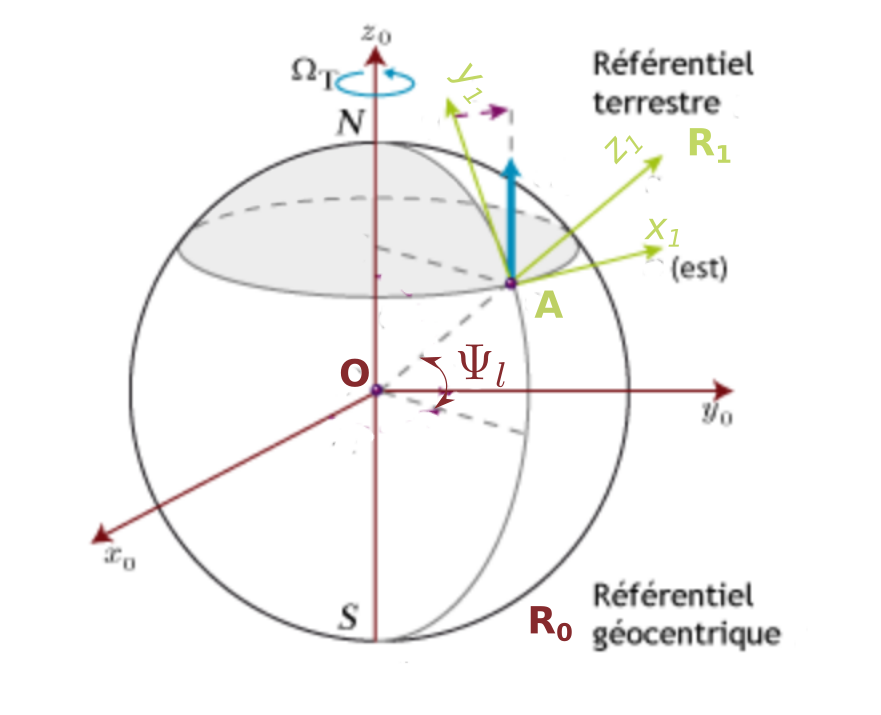
Référentiels et points

$R_0$ référentiel Galiléen (rotation autour de $R_0z$
$R_1$ référentiel du laboratoire ($R_1z$ vertical, $R_1x$ orienté WE, $R_1y$ orienté SN
$O$ centre terre
$A$ point du laboratoire (Pentheon à Paris)

# parametres du problème
l, m, R, g, t = sp.symbols('l m R g t')
# rotation de la terre et lattitude
Omega, Psil = sp.symbols('Omega Psi_l')
# degrés de liberté du pendule
theta, phi = dynamicsymbols('theta phi')

# referentiel fixe
O = Point('O')
R0 = ReferenceFrame("R_0")
# repere lié a la terre
Rt = ReferenceFrame("R_t")
Rt.orient(R0,'Axis',[Omega*t + sp.pi/2, R0.z])
# repere laboratoire R1 et point A
R1 = ReferenceFrame("R_1")
R1.orient(Rt,'Axis',[sp.pi/2-Psil, Rt.x])
A = Point('A')
A.set_pos(O,R*R1.z)

application¶

Calcul de la position et de la vitesse de A dans R0 en utilisant la composition des vitesses:

méthode v1pt_theory()

display("A=",A.pos_from(O).express(R0))
O.set_vel(R0,0)
A.set_vel(R1,0)
A.v1pt_theory(O,R0,R1)
display("VA=",A.vel(R0).express(R0))

'A='

'VA='

position du pendule dans le laboratoire¶

paramètres

l longueur pendule, m masse

ddl

$\theta(t)$ (angle oscillation) et $\phi(t)$ (précession)

forces

tension $T$ dans le cable (suivant $R_3z$)
gravité $g$ suivant $R_1z$

référentiels

$R_1$ référentiel du laboratoire ($R_1z$ vertical)
$R_2$ rotation de $\phi$ autour de $R_1z$
$R_3$ rotation de $\theta$ autour de $R_2y$ lié au pendule
B point fixation du pendule
P position du pendule

# pendule: vertical R1.z , plan oscillation (R1.x,R1.y)
B = Point('B')
B.set_pos(A,l*R1.z)
R2 = ReferenceFrame("R_2")
R2.orient(R1,'Axis',[phi, R1.z])
R3 = ReferenceFrame("R_3")
R3.orient(R2,'Axis',[-theta, R2.y])
P = Point('P')
P.set_pos(B,-l*R3.z)

application¶

Calcul de la position et de la vitesse de P dans R1 en utilisant la composition des vitesses:

méthode v1pt_theory()

display("P=",P.pos_from(A).express(R1))
# Vitesse
B.set_vel(R1,0)
B.v1pt_theory(O,R0,R1)
P.set_vel(R3,0)
P.v1pt_theory(B,R1,R3)
display("VP=",P.vel(R1))

'P='

'VP='

Mouvement du pendule dans R1¶

On néglige dans un premier temps la rotation de la terre, et on étudie le mouvement du pendule dans le référentiel du laboratoire R1

pendule sphérique 3D
hypothèse: R1 repère Galiléen donc pas d'effet de la rotation de la terre

On définit le pendule comme une masse ponctuelle (Particle) de masse m en P dans la variable Pe.

Dans R1, le PFD stipule que la variation de la quantité de mouvement est égale à la somme des forces appliquées:

$$ \frac{d }{dt}m\vec{V_P} = \sum \vec{forces}$$

On commence par calculer la quantité de mouvement (linear_momentum), que l'on dérive dans R1, et on met le résultat dans la variable AP.

On définit ensuite la somme des forces appliquées dans a variable FT:

la tension $\vec{T}$ de module Te suivant R3.z: $$\vec{T}= T_e \;\vec{z_3}$$
le poids $- m g \;\vec{z_1}$

Pe = Particle('Pendule',P,m)
QP = Pe.linear_momentum(R1)
display("Quantité de mvt de P: QP/R1=",QP)
AP = QP.diff(t,R1).simplify()
display("Variation de quantité de mvt de P:  AP/R1=",AP)

'Quantité de mvt de P: QP/R1='

'Variation de quantité de mvt de P:  AP/R1='

# bilan des forces: Tension force de tension de module Te et Poids=m*g poids
Te = sp.symbols('T_e')
Poids   = - m*g*R1.z
Tension = Te*R3.z
FT = Poids + Tension
display("Bilan des forces",FT.express(R3))

'Bilan des forces'

Equations du mouvement dans R1¶

en écrivant le PFD dans R1, on obtiens les 3 équations du mouvement en projetant le PFD dans R3 plutôt que R1 (réfléchissez pourquoi ?)

On va simplifier le système d'équation en introduisant la pulsation propre $\omega_0$ du pendule simple: $$ \omega_0 = \sqrt{\frac{g}{l}} $$ et on va diviser les équations par $ml$

# pulsation propre
omega0 = sp.symbols('omega_0')
# equations du mouvement
EQS=((AP - FT).express(R3).subs(g,omega0**2*l)/(l*m)).simplify()
display("Equations du mvt:",EQS,"= 0")

'Equations du mvt:'

'= 0'

3 équations¶

le système précédent permet obtenir les équations différentielles du mouvement, fonction uniquement des 2 ddl: $\theta, \phi$, avec

une équation sur $\ddot{\theta}$ dans eq1,
une équation sur $\ddot{\phi}$ dans eq2

la dernière équation dans eq3 permet de calculer la tension connaissant $\theta, \phi$

Ecrire les 3 equations dans les variables eq1,eq2 et eq3

eq1 = EQS.dot(R3.x)
display(sp.Eq(eq1,0))
eq2 = EQS.dot(R3.y)
display(sp.Eq(eq2,0))
eq3 = EQS.dot(R3.z)
display(sp.Eq(eq3,0))

Propriétés du système d'équation¶

Pour interpréter les mouvements en mécanique, on cherche des quantités qui se conservent et qui conduisent à des intégrales premières du mouvement. Ces intégrales résultent de l'interprétation des principes fondamentaux de la dynamique:

théorème du moment cinétique: dans un référentiel galiléen, la variation du moment cinétique par rapport à un point fixe O est égale à la somme des moments des forces en O
- conservation du moment cinétique: si le moment des forces est nulle dans une direction fixe, alors il y conservation de la composante du moment cinétique dans cette direction.
théorème de l'énergie: dans un référentiel galiléen, la puissance des forces d'accélération est égale à la variation de l'energie cinétique.
- conservation de l'energie: si les forces qui travaillent sont conservatives, i.e. découlent d'un potentiel (p.e. la gravité), alors il y a conservation de l'énergie totale du système

Appliquons ces principes à notre système en remarquant que les seules forces sont la gravité et la tension:

la gravité est une force conservative découlant d'un potenteil $U_p = m g z_1$ et orienté suivant $R1_z$
la tension ne travaille pas, et passe par le point fixe B

On en déduit 2 intégrales premières

conservation de la composante suivant la verticale $ R_1.z$ du moment cinétique en B
conservation de l'énergie totale $E = E_c + U_p = cste$

calcul des intégrales premières¶

En notant $\omega_1$ la valeur constante de la composante $R_1.z$ du moment cinétique en B divisée par $m l^2$, et $E_0$ la valeur constante de l'énergie cinétique divisée aussi par $m l^2$, calculez les 2 intégrales premières en fonction uniquement de $\theta$ et $\phi$ et des ces deux constantes dans les variables eq10 (pour l'énergie) et eq21 (pour le moment cinetique)

# constantes (/ par ml**2)
omega1, E0 = sp.symbols('omega_1 E_0')
# calcul mt cinetique et energie
mc_z = Pe.angular_momentum(B,R1).dot(R1.z)
display("mt cinetique suivant z1: mc_z ",sp.Eq(mc_z,omega1*m*l**2))
Ec = Pe.kinetic_energy(R1)
Up = m*g*P.pos_from(B).dot(R1.z)
Et = Ec + Up
display("énergie totale: Et",sp.Eq(Et,E0*m*l**2))

'mt cinetique suivant z1: mc_z '

'énergie totale: Et'

# calcul des 2 intégrales premieres avec introduction de omega0
eq21 = mc_z/(m*l**2)
eq10 = ((Ec+Up)/(m*l**2)).subs(g,omega0**2*l).simplify()
display("conservation mt cinetique:",sp.Eq(eq21,omega1))
display("conservation énergie:",sp.Eq(eq10,E0))

'conservation mt cinetique:'

'conservation énergie:'

simplification du système d'équation¶

Nous allons remplacer l'équation sur $\ddot{\phi}$ par la conservation du moment cinétique suivant $R_1.z$, qui nous donne directement $\dot{\phi}$ en fonction de $\theta$, que nous pouvons donc remplacer dans l'équation sur $\ddot{\theta}$ pour obtenir une équation uniquement en $\theta$. On écrira les equations sous la forme

$\ddot{\theta} = $ eq11
$\dot{\phi} = $ eq22
$ E_0 = $ eq00

L'équation de conservation de l'énergie que l'on simplifie aussi nous servira à valider notre solution numérique.

# calcul des second membres
eq22 = omega1/sp.sin(theta)**2
display("Conservation Mt cinetique: ",sp.Eq(phi.diff(t),eq22))
# substitution de dphi/dt dans les 2 autres equations
cdt_phi = [(phi.diff(t),eq22)]
# equation sur theta
eq11 = (theta.diff(t,2)-eq1.subs(cdt_phi)).simplify()
display("Equation sur theta:",sp.Eq(theta.diff(t,2),eq11))
# equation conservation energie
eq00 = eq10.subs(cdt_phi).simplify()
display("Conservation energie:",sp.Eq(eq00,E0))

'Conservation Mt cinetique: '

'Equation sur theta:'

'Conservation energie:'

analyse du système d'EDO dans 2 cas limites¶

vérification du système d'équations

cas sans précession $\dot{phi}=0$¶

Si on ne donne pas de mouvement initial de précession, i.e. $\dot{\phi} = 0$, alors on a $\omega_1=0$, ce qui donne pour l'équation sur $\ddot{\theta}$:

$$ \ddot{\theta} = -\omega_0^2 \sin{\theta}$$

qui correspond à l'équation du pendule simple, qui pour de petits angles $\theta$ $$ \ddot{\theta} = -\omega_0^2 \theta$$ a une solution harmonique $$ \theta = \theta_0 \cos{\omega_0 t} $$

cas avec une forte précession initiale¶

On suppose maintenant que $\dot{\phi}$ est grand devant $\dot{\theta}\approx 0$ que l'on néglige. On a alors $\theta(t)=cste=\theta_0$. Dans ce cas la vitesse de precéssion est constante et vaut: $$\dot{\phi} = \frac{\omega_1}{\sin^2{\theta_0}}= cste$$ le pendule décrit alors des cercles d'axes $R_1.y$ et de rayon $l\sin\theta_0$

Simulation numérique¶

on trouvera en annexe à la fin du notebook la simulation numérique du pendule sphérique et la visualisation 3D de sa trajectoire.

Prise en compte de la rotation de la terre¶

On considère maintenant la rotation de la terre

le référentiel du laboratoire $R_1$ n'est plus galiléen et est en rotation avec la terre
le point P est mobile dans $R_1$, donc sa vitesse / $R_0$ s'écrit:

$$\underbrace{\overrightarrow{V}^{\,R_0}_P}_\textrm{V absolue} = \underbrace{\overrightarrow{V}^{\,R_1}_P}_\textrm{V relative} + \underbrace{\overrightarrow{V}^{\,R_0}_B + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{BP}}_\textrm{V entraînement}$$

de même l'accélération de P / $R_0$ s'écrit

\begin{eqnarray} \underbrace{\overrightarrow{\gamma}^{\,R_0}_P}_\textrm{absolue} & = & \underbrace{\overrightarrow{\gamma}^{\,R_1}_P}_\textrm{relative} + \underbrace{\overrightarrow{\gamma}^{\,R_0}_B + \dot{\overrightarrow{\Omega}}_{R_1/R_0} \wedge \overrightarrow{BP} + \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{BP}}_\textrm{entraînement}\\ & + & \underbrace{2 \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{V}^{\,R_1}_P}_\textrm{coriolis}\\ \end{eqnarray}

Dans notre cas la vitesse de rotation de la terre est constante $\dot{\Omega} = 0$ et on ne conserve que les termes d'ordre 1 en $\Omega$ \begin{eqnarray} \underbrace{\overrightarrow{\gamma}^{\,R_0}_P}_\textrm{absolue} & = & \underbrace{\overrightarrow{\gamma}^{\,R_1}_P}_\textrm{relative} + \underbrace{2 \overrightarrow{\Omega}_{R_1/R_0} \wedge \overrightarrow{V}^{\,R_1}_P}_\textrm{coriolis} \end{eqnarray}

Ordre de grandeur¶

calcul de la vitesse et accélération de B / à R0
calcul de la vitesse et accélartion de P / à R1
composition des vitesses et accélération
terme prépondérant: Coriolis

# vitesse de rotation de R1/R0
display("W R1/R0=",R1.ang_vel_in(R0).express(R1))
# vitesse et accélaeration de B dans R0
display("VB = ",B.vel(R0).express(R1))
# acceleration de B
display("AB = ",B.acc(R0).express(R1))

'W R1/R0='

'VB = '

'AB = '

# vitesse et accélération de P / R1
VP = P.vel(R1)
display("VP/R1=",VP)
AP = P.acc(R1)
display("AP/R1=",AP)
# vitesse et accélération de P / R0 par application de la composition 
display("VP/R0=",P.v1pt_theory(B,R0,R1).express(R3).simplify())
# calcul acceleration de P dans R0
display("AP/R0=",P.a1pt_theory(B,R0,R1).express(R3).simplify())

'VP/R1='

'AP/R1='

'VP/R0='

'AP/R0='

# calcul de l'accélération de Coriolis dans AC
AC = 2*R1.ang_vel_in(R0).cross(VP).express(R3).simplify()
display("AC=",AC)
# calcul de l'acceleration de P/R0 en prenant en compte que le terme lineaire en Omega
AP0 = AP + AC
display("AP/R0=",AP0)

'AC='

'AP/R0='

# vérification le terme negligé est proportionnel à Omega**2
display("terme négligé pour AP/R0:")
(AP0 - P.a1pt_theory(B,R0,R1).express(R3).simplify()).simplify()

'terme négligé pour AP/R0:'

PFD avec la force de Coriolis¶

On se place dans le référentiel du laboratoire R1, et dans ce cas l'accélération de Coriolis $\gamma_c$ apparaît une force de Coriolis $-m \vec{\gamma_c}$ supplémentaire agissant sur le pendule:

$$ \frac{d }{dt} m\vec{V_P} = \sum \vec{forces}$$

avec $$\sum \vec{forces} = -mg \vec{z1} + Te \vec{z3} - m \vec{\gamma_c} $$

calculer le bilan des forces dans FT
en déduire les équations du mouvement dans EQS (sous la forme EQS=0)

# bilan des forces
Poids   = - m*g*R1.z
Tension = Te*R3.z
# coriolis (attention signe)
Fc      = -m*AC
FT = Poids + Tension + Fc
display("bilan des forces dans R1: FT=",FT.express(R3))
EQS = m*AP - FT
display("équations dans R1: EQS=",EQS)

'bilan des forces dans R1: FT='

'équations dans R1: EQS='

Equations du mouvements¶

On obtiens les 2 équations du mouvement par projection suivant R3.x et R3.y (perpendiculaire à la tension), en divisant par $ml$ et en introduisant $\omega0=\sqrt{\frac{g}{l}}$

Mettre le résultat dans les variables eq1c et eq2c

# equations du mouvement projete dans R3
eq1c = (EQS.dot(R3.x).subs(g,omega0**2*l)/(l*m)).expand()
display("equation suivant R3.x:",sp.Eq(eq1c,0))
eq2c = (EQS.dot(R3.y)/(l*m)).expand()
eq2c = (eq2c).expand()
display("equation suivant R3.y:",sp.Eq(eq2c,0))

'equation suivant R3.x:'

'equation suivant R3.y:'

Analyse¶

Retrouve t'on les propriétés de conservation du pendule sphérique ?

si on calcule le moment de la force de Coriolis en B, elle a une composante suivant R1.z:
- on a donc plus de conservation du moment cinetique suivant R1.z. C'est le signe de l'influence de la rotation de la terre sur le mouvement du pendule.
- on ne peut donc plus simplifier l'équation sur $\phi$ comme dans le cas du pendule sphérique
par contre la force de Coriolis ne travaille pas (pourquoi ?). Sa puissance est nulle
- on a donc conservation de l'énergie totale comme dans le cas du pendule sphérique, ce qui nous permettra de vérifier la précision de notre modèle numérique

C'est ce que nous allons vérifier

# moment en B des forces : projection suivant R1.z
display("Moment en B des forces:",P.pos_from(B).cross(FT).express(R1))
# puissance  des forces de coriolis
display("Puissance de la force de Coriolis:",AC.dot(VP).simplify())

'Moment en B des forces:'

'Puissance de la force de Coriolis:'

Résolution numérique¶

Les 2 EDO du mouvement dans eq1c et eq2c s'écrivent sous la forme:

$\ddot{\theta} = f_{1c}(\theta,\phi)$
$\ddot{\phi} \sin\theta = f_{2,c}(\theta,\phi)$

# 1ere equation
display("equation sur theta eq1c=",sp.Eq(eq1c,0))
# second membre
f1c = theta.diff(t,2) - eq1c
display("sous forme EDO:",sp.Eq(theta.diff(t,2),f1c))
# 2nde equation
display("equation sur phi: eq2c=",sp.Eq(eq2c,0))
f2c = phi.diff(t,2)*sp.sin(theta) - eq2c
display("sous forme EDO:",sp.Eq(phi.diff(t,2)*sp.sin(theta),f2c))

'equation sur theta eq1c='

'sous forme EDO:'

'equation sur phi: eq2c='

'sous forme EDO:'

simplification¶

On s'interesse à la solution pour des petits angles $\theta$.

Or l'équation 2 sur $\ddot{\phi}$ dégénére à cause du terme en $\sin\theta$ qui tends vers zéro.

On va donc simplifier la seconde équation en négligeant les termes en $\sin\theta$ et en divisant par $2\dot{\theta}\cos\theta$.

Attention on ne néglige pas les termes en $\sin\theta$ dans la première équation car tous les termes sont d'ordre $\sin\theta$ , ce qui n'est pas le cas dans la seconde.

# simplification seconde equation
eq3c = (eq2c.subs(sp.sin(theta),0)/(2*sp.cos(theta)*theta.diff(t))).expand()
display("Equation sur phi simplifiée:",eq3c)
f3c = phi.diff(t)-eq3c
display("sous forme EDO: ",sp.Eq(phi.diff(t),f3c))

'Equation sur phi simplifiée:'

'sous forme EDO: '

système d'équations simplifiées¶

La nouvelle équation impose donc : $$\dot{\phi} = - \Omega \sin\Psi_l$$ c.a.d. une vitesse de précession $\phi$ constante dans le sens horaire dans l'hémisphère Nord et anti-horaire dans l'hémisphère Sud.

Le système d'équation à résoudre s'écrit, en remplaçant $\dot{\phi]}$ dans la première équation:

\begin{eqnarray} \ddot{\theta} &=& f_{1c}(\theta,\dot{\theta},\phi)\\ \dot{\phi} &=& - \Omega \sin\Psi_l \end{eqnarray}

On définit les valeurs numériques pour ensuite convertir le second membre f1c en fonction python F1c et calculer la valeur numérique de F3c

# parametres du Pendule Foucault Pantheon
# ========================================
L0 = 67.
OMEGA0 = np.sqrt(9.81/L0)
# lattitude en degre
Lat = 48.5
# periode rotation terre 23h56
OMEGA  = 2*np.pi/(23*3600+56*60)
print("Omega0={:.2e} Omega={:.2e} ".format(OMEGA0,OMEGA))

Omega0=3.83e-01 Omega=7.29e-05

# valeurs numériques des parametres
valnums = [(omega0,OMEGA0),(Omega,OMEGA), (Psil,np.deg2rad(Lat))]
display("valeurs des parametres: ",valnums)
# equations
display("Equation sur theta: eq1c=",sp.Eq(theta.diff(t,2),f1c))
display("Equation sur phi  : eq3c=",sp.Eq(phi.diff(t),f3c))
# convertion des seconds memebres  en fonction python F1c et F2c
F1c = sp.lambdify([theta,theta.diff(t),phi],f1c.subs(phi.diff(t),f3c).subs(valnums))
F3c = float(f3c.subs(valnums))

'valeurs des parametres: '

'Equation sur theta: eq1c='

'Equation sur phi  : eq3c='

Mise sous forme d'équation du 1er ordre¶

Le système d'équation à résoudre est un système du second ordre \begin{eqnarray} \ddot{\theta} &=& f_{1c}(\theta,\phi,\dot{\theta},\dot{\phi}) \\ \dot{\phi} &= &- \Omega \sin\Psi_l \end{eqnarray}

que l'on va transformer en un système du premier ordre en prenant comme variable d'etat $$ Y = [\theta, \dot{\theta}, \phi ]$$

Le système à résoudre s'écrit alors :

\begin{equation} \dot{Y} = F(Y,t) \mbox{ avec } F(Y,t) = \begin{bmatrix} Y_3 \\ f_{1,c}(Y_1,Y_2,Y_3)\\ Y_4 \\ \end{bmatrix} \end{equation}

On définit une fonction second membre penduleFoucault().

def penduleFoucault(etat, temps=0):
    '''
    calcul le second membre du pendule de Foucault
    
    Arguments
    ---------   
    etat :  vecteur d'etat [theta, dtheta, phi]
    temps:  instant t du calcul
    
    Retour 
    -------
    derivs:  derivée du vecteur d'etat 
    '''
    global F1c, F3c

    derivs = np.array([etat[1],F1c(etat[0],etat[1],etat[2]), F3c])
    return derivs

def iterationRK2(etat, smb, temps, dt):
    '''Iteration de RungeKutta 2 pour calculer l'évolution de l'etat sur un pas en temps. 
    
    Arguments
    ---------
    etat : vecteur d'etat
    smb  : fonction qui calcule le second membre de l'EDO fonction de l'etat et du temps
    temps: instant du début du calcul
    dt   : pas en temps 
    
    Retour
    -------
    etat_suiv: movelle valeur du vecteur d'etat après une iteration en temps       
    '''
    etat_milieu = etat + smb(etat,temps) * dt*0.5
    etat_suiv   = etat + smb(etat_milieu,temps) *dt
    return etat_suiv

résolution numérique¶

démarche

définition des paramétres

Le pendule de Foucault fait $L_0=67m$ de longueur et on le lache à 1m de sa position d'équilibre

calcule de la CI

on lache le pendule avec un angle $\theta_0$ petit dans la direction $R_1.x$ (lattitude WE) sans vitesse initiale $\dot{\theta}(0)=0$

$$ \theta_0 \approx \frac{1}{L_0}$$

la solution prédit une précession constante de $\Omega \sin{\Psi_l}$ autour de $R1_z$ dans le sens horaire

choix du pas en temps et temps de simulation

on choisit une durée d'étude de 4h et 400 pas en temps par période du pendule

on effectue des iterations de Runge Kutta pour calculer la solution numérique
on annalyse le résultat et on vérifie les propriétés de conservation

# valeurs des parametres
CI = [1./L0, 0., np.pi/2]
print("CI=",CI)
# temps d'étude 
dt = (2*np.pi/OMEGA0)/400
TT = 4*3600
N  = round(TT/dt)
TT = N*dt
tt = np.linspace(0, TT, N)
print("parametres: N={} dt={:.2e} T={:.2e}".format(N,dt,TT))

CI= [0.014925373134328358, 0.0, 1.5707963267948966]
parametres: N=350784 dt=4.11e-02 T=1.44e+04

# integration numérique: attention le calcul peut etre long !!!
sol_num = np.zeros([N,3])
sol_num[0] = CI
# iteration en temps
for i in range(N-1):
    sol_num[i+1] = iterationRK2(sol_num[i], penduleFoucault, tt[i], dt)
# solution theta et phi
Theta = sol_num[:,0]
dTheta= sol_num[:,1]
Phi   = sol_num[:,2]
# position du pendule X,Y,Z
X =  L0*np.sin(Theta)*np.cos(Phi)
Y =  L0*np.sin(Theta)*np.sin(Phi)
Z =  L0-L0*np.cos(Theta)

Visualisation de la solution¶

on visualise les angles $\theta(t)$ et $\phi(t)$ en utilisant des unités plus parlantes que les unités SI:

angle en degré
temps en minute

et on fait un zoom pour $\theta(t)$ dont l'évolution est beaucoups plus rapide que celle de $\phi(t)$

plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.title("Angle d'oscillation $\\theta(t)$ et de précession $\phi(t)$")
plt.plot(tt/60,np.rad2deg(Theta))
plt.ylabel("$\\theta(t)$ en degré")
plt.xlim(0,10)
plt.subplot(2,1,2)
plt.ylabel("$\phi(t)$ en degré")
plt.plot(tt/60,np.rad2deg(Phi))
plt.xlabel("temps [mn]");

plt.figure(figsize=(8,8))
plt.plot(X,Y)
plt.title("Trajectoire du pendule dans le plan X,Y du panthéon")
plt.xlabel('x')
plt.xlabel('y')
plt.plot(X[0],Y[0],'*',markersize=14,color='k')
draw_circle = plt.Circle((0., 0.), L0*np.sin(CI[0]),fill=False)
plt.gcf().gca().add_artist(draw_circle)
plt.axis('equal');

Visualisation 3D¶

visualisation 3D pendant un temps court et en accéléré

# selection de la partie de la solution à visualiser
pas = 10
fin = 3000
XX = X[:fin:pas]
YY = Y[:fin:pas]
ZZ = Z[:fin:pas]
TT = tt[:fin:pas]

from validation.Pendule3D import PenduleFoucault
# tracer de la position initiale
PF = PenduleFoucault(XX,YY,ZZ,TT,L0)
PF.trace(L0/20)

# zoom et tracer de la trajectoire
PF.plot.camera = [L0/10,L0/15,L0/15] + [0,0,0] + [0,0,1]
PF.traj3D()

Validation du calcul¶

comparaison avec le calcul théorique de Foucault obtenu par linéarisation des équations dans le plan
vérification de la conservation de l'énergie totale

# precession theorique (analyse de Foucault)
OMEGA1 = OMEGA*np.sin(np.deg2rad(Lat))
# verification periode en heures
Phip = (Phi[-1]-Phi[100])/(tt[-1]-tt[100])
print("Periode precession {:.4f} h (theorique {:.4f} h)".format(-2*np.pi/Phip/3600, 2*np.pi/OMEGA1/3600))

Periode precession 31.9557 h (theorique 31.9556 h)

display("Energie:",sp.Eq(eq10,E0))
eq10a = eq10.subs([(omega0,OMEGA0),(phi.diff(t),-OMEGA1)])
Et = sp.lambdify([theta,theta.diff(t)], eq10a)
ET = Et(Theta,dTheta)
plt.figure(figsize=(10,4))
plt.plot(tt,(ET-ET[0])/ET[0])
plt.xlabel('temps [s]')
plt.ylabel('erreur en %')
plt.title("Erreur relative sur l'énergie");

'Energie:'

Conclusion¶

On observe bien une rotation du plan d'oscillation dans le sens de rotation des aiguilles d'une montre

C'est le contraire dans l'hémisphère nord.

La précision de la méthode de RUnge Kutta 2 sur des temps très longs oblige à prendre des pas en temps très petits

Si on mesure la période de précésion, on peut alors en déduire soit la lattitude $\Psi_l$ soit la vitesse de rotation de la terre $\Omega$

Le pendule que Foucault a installé au Panthéon en 1851 mesurait 67 mètres et portait une masse de 28 kilogrammes. Une fois lancé, ce pendule oscille pendant 6h. La période (aller-retour) étant de 16,5 s, le pendule dévie de 11° par heure. Il faut donc de l'ordre de 32 heures pour une rotation complète du plan d'socillation. Depuis 1995, ce pendule est à nouveau au Panthéon.

ANNEXE 1: solution Analytique¶

en linéarisant le système d'équation précédent, on peut obtenir une solution analytique, semblable à la solution obtenue par Foucault.

En supposant que le mouvement du pendule reste dans le plan (R1.x,R1.z) et on néglige la variation suivant la verticale R1.y, il choisit alors comme ddl la position $x_p(t), y_p(t)$ du pendule dans le plan horizontale en supposant $z_p(t)=cste=0$

On va linéariser les équations du pendule de Foucault en supposant $\theta$ petit, i.e. $$\sin\theta \approx \theta \mbox{ et } \cos\theta \approx 1 $$ et en conservant uniquement les termes d'ordre 1 en $\theta$

# equations du pendule de Foucault
display("Equation sur theta: eq1c=",sp.Eq(theta.diff(t,2),f1c))
display("Equation sur phi  : eq3c=",sp.Eq(phi.diff(t),f3c))

'Equation sur theta: eq1c='

'Equation sur phi  : eq3c='

# equations linéarisées
f1cl = f1c.subs([(sp.sin(theta),theta),(sp.cos(theta),1),
                 (theta**2,0),(phi.diff(t),f3c)])
display("Equation sur theta linearisée:",sp.Eq(theta.diff(t,2),f1cl))
display("Equation sur phi             :",sp.Eq(phi.diff(t),f3c))

'Equation sur theta linearisée:'

'Equation sur phi             :'

solution analytique¶

ces équations différentielles linéaires admettent une solution analytique simple

$$ \theta(t) = \theta_0 \cos{\left( (\omega_0 + \Omega\sin{\Psi_l}) t\right)} $$$$ \phi(t) = \frac{\pi}{2} -\Omega\sin(\Psi_l) t $$

theta0 = sp.symbols('theta_0')
thetal = theta0*sp.cos((omega0+Omega*sp.sin(Psil))*t)
phil   = sp.pi/2 - Omega*sp.sin(Psil)*t
display("Solution analytique:",sp.Eq(theta,thetal),sp.Eq(phi,phil))

'Solution analytique:'

# évaluation numérique
Theta0 = CI[0]
Thetal = sp.lambdify([t],thetal.subs(valnums).subs(theta0,Theta0))
Phil   = sp.lambdify([t],phil.subs(valnums))
# calcul solution
ThetaL = Thetal(tt)
PhiL   = Phil(tt)

solution exacte¶

pour évaluer l'erreur de modélisation liée à la linéarisation, nous allons résoudre numériquement les équations du mouvement du pendule de Foucault avec une methode numérique très précise en utilisant la fonction odeint de la bibliothèque scipy.integrate

# calcul de la solution numérique avec la methode odeint plus précise que RK2
from scipy.integrate import odeint
sol = odeint(penduleFoucault, CI, tt)
ThetaE = sol[:,0]
PhiE   = sol[:,2]

plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.title("Ecart avec la solution exacte")
plt.plot(tt/60,(ThetaL-ThetaE),label="$\\theta_l - \\theta_e$")
plt.plot(tt/60,(Theta -ThetaE),label="$\\theta   - \\theta_e$")
plt.ylabel("$\\theta(t)-\\theta_l(t)$")
plt.xlim(100,120)
plt.legend()
plt.subplot(2,1,2)
plt.ylabel("$\phi(t)-\phi_l(t)$ ")
plt.plot(tt/60,PhiL-PhiE, label="$\phi_l - \phi_e$")
plt.plot(tt/60,Phi -PhiE, label="$\phi   - \phi_e$")
plt.legend()
plt.xlabel("temps [mn]");

analyse¶

on constate que la solution $\theta_l$ linéarisée en $\theta$ qui prédit une oscillation périodique avec une pulsation $$\omega = \omega_0 + \Omega\sin{\Psi_l}$$ s'écarte de plus en plus de la solution exacte des équations, ce qui tend a montrer l'importance des termes non-linéaires, même pour des faibles oscillations. La solution numérique RK2 présente une erreur d'intégration, mais qui reste plus faible que cette erreur de modélisation liée à la linéarisation.

Cependant le mouvement de précession n'est pas affecté par ces erreurs sur $\theta$, car la vitesse de précession est constante et égale à :

$$ \dot{\phi} = -\Omega\sin\Psi_l$$

ANNEXE 2: étude numérique du mvt 3D du pendule¶

sans prise en compte de l'accélération de Coriolis, nous allons simuler les équations générales du pendule 3d et visualiser les trajectoires en 3D

Intégration numérique¶

On considère donc le système d'équations \begin{eqnarray} \ddot{\theta} &=& \frac{\omega_1^{2} \cos{\left(\theta{\left(t \right)} \right)}}{\sin^{3}{\left(\theta{\left(t \right)} \right)}} - \omega_{0}^{2} \sin{\left(\theta{\left(t \right)} \right)} \\ \dot{\phi} &=& \frac{\omega_1}{\sin(\theta)^2} \end{eqnarray}

soit en $Y = \left[\theta, \dot{\theta}, \psi \right]$ \begin{eqnarray} \dot{Y_1} &=& Y_2 \\ \dot{Y_2} &=& \frac{\omega_1^{2} \cos{Y_1}}{\sin^{3}{Y_1}} - \omega_{0}^{2} \sin{Y_2} \\ \dot{Y_3} &=& \frac{\omega_1}{\sin(Y_1)^2} \end{eqnarray}

La valeur de $\omega_1$ est déterminée par les conditions initiales CI: $$\theta(0) = \theta_0,\; \dot{\theta}(0) = 0,\; \psi(0) = 0, \; \dot{\psi}(0) = d\psi_0 $$ ce qui fixe la valeur de $\omega_1$ $$ \omega_1 = d\psi_0 \sin{\theta_0}^2 $$

Algorithme

calcul de la valeur des parametres et des CI pour un pendule de longueur L=1 avec g=9.81
- variables CI, Omega0, Omega1 , L et valsnum
calcul du second membre dans une fonction pendule3D
utilisation de la fonction iterationRK2
boucle d'itération en temps pour calculer la solution

# 1. calcul des CI et des valeurs des parametres valnums
# CI
CI = [np.pi/5, 0, 0, 2*np.pi/5]
display("CI=",CI)
# parametres numeriques
L = 1.0
Omega0 = np.sqrt(9.81/L)
Omega1  = CI[3] * np.sin(CI[0])**2
valnums = [(l,L),(omega0,Omega0),(omega1,Omega1)]
display("parametres:",valnums)

calcul de la fonction second membre¶

transformation du second membre de l'équation en $\ddot{\theta}$ a partir de l'expression analytique en utilisant la fonction sympy lambdify

 Ftheta = sp.lambdify([theta,omega0,omega1],expression)

Ecriture de la fonction pendule3D qui calcul le second membre en fonction du vecteur d'etat dans la variable etat et du temps temps

Ftheta = sp.lambdify([theta,omega0,omega1],eq11,'numpy')

def pendule3D(etat, temps=0):
    '''
    calcul le second membre du pendule sphérique 3D
    
    Arguments
    ---------   
    etat :  vecteur d'etat [theta, dtheta, phi]
    temps:  instant t du calcul
    
    Retour 
    -------
    derivs:  derivée du vecteur d'etat 
    '''
    global Ftheta,Omega1,Omega0
    
    derivs = np.array([etat[1], Ftheta(etat[0],Omega0,Omega1), Omega1/np.sin(etat[0])**2])
    return derivs

iteration de calcul¶

On fait une calcul sur 5 périodes du pendule simple avec 500 points de calcul par période.

# integration
period = 2*np.pi/Omega0
dt = period/500
TT = 5*period
N  = round(TT/dt)
tt = np.linspace(0, TT, N)
# solution par la méthode RK2
num_sol = np.zeros([N,3])
#Set intial conditions
num_sol[0,:] = CI[:3]
# calcul de la solution 
for i in range(N-1):
    num_sol[i+1] = iterationRK2(num_sol[i], pendule3D, tt[i], dt)

tracé de la solution¶

On trace l'évolution de $\theta$ et $\phi$ au cours du temps

attention pour les angles on doit raméner les valeurs entre 0 et $2\pi$ avec la fonction modulo (pourquoi ?)

On vérifie le calcul en traçant l'énergie totale en fonction du temps en utilisant lambdify

# fonction de calcul de l'energie 
Et = sp.lambdify([theta,theta.diff(t),omega0,omega1],eq00)
# calcul de la solution à tracer
Theta = num_sol[:,0]
dTheta= num_sol[:,1]
Phi   = np.mod(num_sol[:,2], 2*np.pi)
ET = Et(Theta,dTheta,Omega0,Omega1)

# tracer
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(tt,Theta,label="$\\theta(t)$")
plt.plot(tt,Phi,label="$\\phi(t)$")
plt.xlabel('t [s]')
plt.ylabel("Angles [rd]")
plt.legend()
plt.title("Angles et erreur sur l'énergie totale.\n")
plt.subplot(2,1,2)
plt.plot(tt,(ET-ET[0])/ET[0])
plt.xlabel('t [s]')
plt.ylabel("erreur relative");

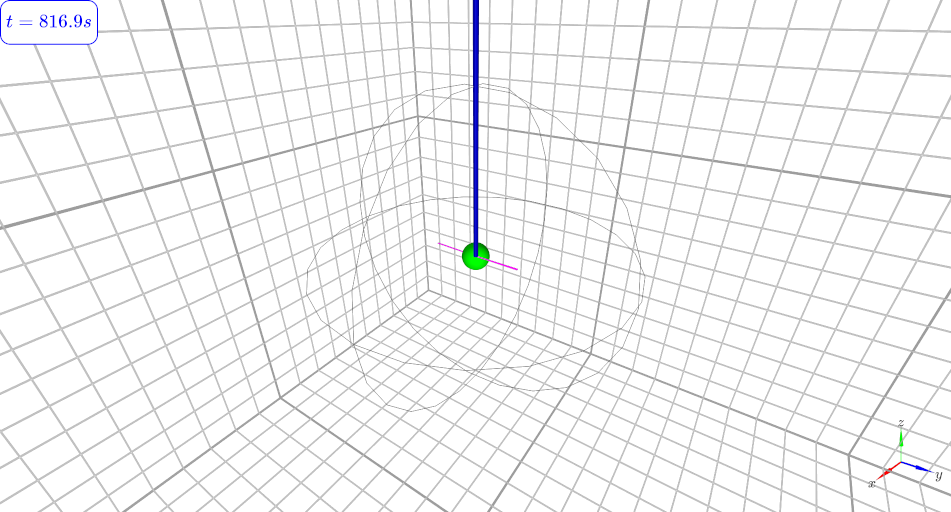
Visualisation 3D des trajectoires (petites oscillations)¶

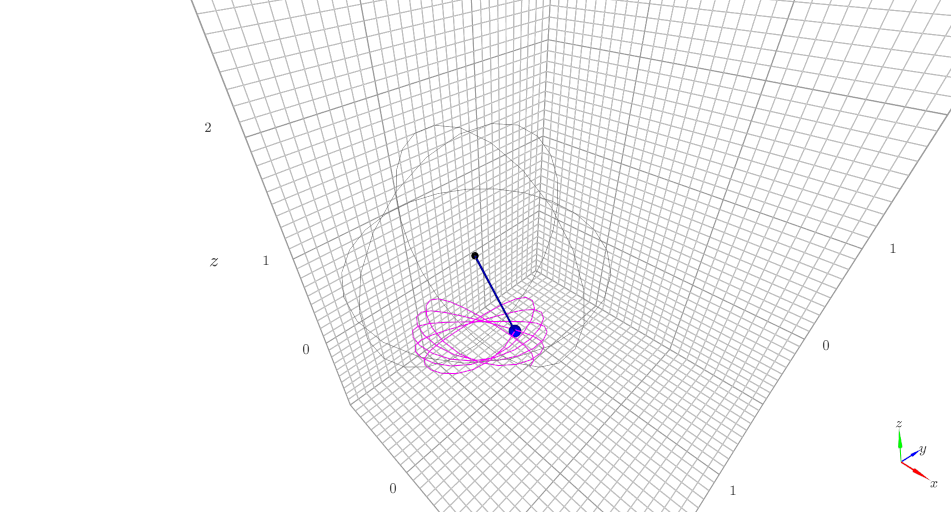
from validation import Pendule3D
pendule3d = Pendule3D.Pendule3D(Ftheta,Omega0,L)
pendule3d.solution(CI,tt[::25])
pendule3d.trace3D()

Visualisation 3D dans le cas avec de grandes amplitudes¶

vous pouvez expérimenter en choisisant des CI différentes, p.e.

oscillation pendule simple (precession nulle)
précession rapide (cercle)

pendule3d.solution([np.pi/2,0.,0.,1.5*np.pi/2],tt[::10])
pendule3d.trace3D()

FIN¶

# version
from platform import python_version,uname,platform
print("Systeme       :",uname())
print("OS            :",platform())
print("version python:",python_version())
print("version sympy :",sp.__version__)
print("version numpy :",np.__version__)