4.4. TP Numpy & Matplotlib#
Marc BUFFAT, dpt mécanique, Université Lyon 1
# bibliotheque
import os,sys
import numpy as np
import matplotlib.pyplot as plt
#
from IPython.display import Markdown, display
plt.rc('font', family='serif', size='16')
# bibliotheque
from validation.validation import check_function,liste_functions,info_function,info_etudiant, bib_validation
from validation.valide_markdown import test_markdown, test_code
bib_validation('cours','MGC2028L')
def printmd(string):
display(Markdown(string))
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
# test si numero étudiant spécifier
if type(NUMERO_ETUDIANT) is not int :
NOM, PRENOM, NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
_x0_ = 2*(1-2*np.random.rand())
_x1_ = 2*(1-2*np.random.rand())
if _x0_>_x1_ : _x0_,_x1_ = _x1_,_x0_
_c_ = 1. + np.random.rand()
F = lambda x : _c_*(x-_x0_)*(x-_x1_)
printmd("**Etudiant** {} {} id={}".format(NOM,PRENOM,NUMERO_ETUDIANT))
Etudiant Marc BUFFAT id=137764122
4.4.1. Objectif : étude d’une fonction#
On se propose d’étudier une fonction F(x) dont la valeur numérique pour chaque valeur de x nous est fournie par une fonction \(F(x)\). On sait que sur l’intervalle [-2,2], la fonction admet 2 racines et possède un minimum entre ces 2 racines.
L’objectif est de déterminer les valeurs (approchées) de ces 2 racines \(r_1\) et \(r_2\) et de la position du minimum \(x_m\) en utilisant différentes approches numériques:
avec la méthode la plus simple: on calcule la valeur de F dans un tableau Y en se donnant un tableau de points X, et on en déduit les valeurs à partir de X et Y
avec un algorithme numérique de dichotomie pour les racines et son extension pour la position du minimum
avec une interpolation par un polynôme d’ordre 2
4.4.2. Etude numérique de la fonction#
En utilisant la fonction numpy linspace, déterminer un tableau X contenant 51 valeurs
équi-répartis entre \([-2,2]\). En utilisant la fonction python \(F(x)\) fournie, en déduire un tableau Y
contenant les valeurs de F associées.
En utilisant une boucle, afficher toutes les valeurs de ces 2 tableaux sous la forme de 2 colonnes x et y
avec un affichage qui tronque la partie décimale à 6 chiffres en utilisant format.
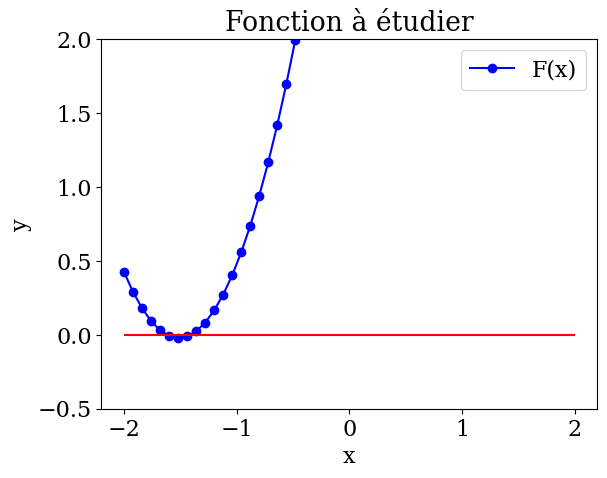
En utilisant les fonctions de matplotlib, tracer la fonction en bleu en mettant des markers (“b-o”). Rajouter des axes, un titre et la droite y=0 en rouge.
En utilisant xlim et ylim, zoomer sur la zone où se trouvent à la fois les racines et le minimum.
import numpy as np
import matplotlib.pyplot as plt
# calcul des valeurs
## BEGIN SOLUTION
X = np.linspace(-2,2,51)
Y = F(X)
for i in range(X.size):
print("{:.6f} {:.6f}".format(X[i],Y[i]))
# Alternative introduite avec Python 3.6 et la PEP 498
# print(f"X = {X[ind]:.6f} ,Y = {Y[ind]:.6f}")
## END SOLUTION
# tracer
## BEGIN SOLUTION
plt.plot(X,Y,'b-o',label="F(x)")
plt.hlines(0.,X[0],X[-1],color='r')
plt.xlabel('x')
plt.ylabel('y')
plt.title("Fonction à étudier")
# zoom (a adapter)
#plt.xlim(-0.5,1.)
plt.ylim(-0.5,2)
plt.legend()
## END SOLUTION
-2.000000 0.425808
-1.920000 0.290982
-1.840000 0.180312
-1.760000 0.093799
-1.680000 0.031442
-1.600000 -0.006758
-1.520000 -0.020803
-1.440000 -0.010691
-1.360000 0.023577
-1.280000 0.082001
-1.200000 0.164582
-1.120000 0.271318
-1.040000 0.402211
-0.960000 0.557260
-0.880000 0.736466
-0.800000 0.939828
-0.720000 1.167345
-0.640000 1.419020
-0.560000 1.694850
-0.480000 1.994837
-0.400000 2.318979
-0.320000 2.667279
-0.240000 3.039734
-0.160000 3.436345
-0.080000 3.857113
0.000000 4.302037
0.080000 4.771117
0.160000 5.264354
0.240000 5.781747
0.320000 6.323296
0.400000 6.889001
0.480000 7.478862
0.560000 8.092880
0.640000 8.731054
0.720000 9.393384
0.800000 10.079871
0.880000 10.790513
0.960000 11.525312
1.040000 12.284267
1.120000 13.067379
1.200000 13.874646
1.280000 14.706070
1.360000 15.561650
1.440000 16.441386
1.520000 17.345279
1.600000 18.273328
1.680000 19.225533
1.760000 20.201894
1.840000 21.202411
1.920000 22.227085
2.000000 23.275915
<matplotlib.legend.Legend at 0x7fc2bb3271c0>
# ne pas modifier
## BEGIN HIDDEN TESTS
assert(test_code("TP_numpy.ipynb","cell-verif01",
["plt.plot","plt.title","plt.xlabel","plt.ylabel"]))
## END HIDDEN TESTS
4.4.3. Approximation des racines à partir des tableaux X,Y#
Principe: Une première approximation des racines est obtenue en cherchant dans le tableau Y les 2 valeurs les plus proches de 0., puis en déduisant les valeurs de X correspondantes. On procède de façon identique avec le minimum.
Mise en oeuvre pratique: Pour les racines, on cherche dans le tableau Y, les 2 points proches de 0. : i.e. tq \(|Y_i| < \epsilon\), où \(\epsilon\) est une petite valeur.
Indications : Pour sélectionner des éléments, on peut utiliser la propriété de sélection des éléments d’un tableau numpy en passant une condition à la place de la sélection des indices. Cette condition doit être un tableau de valeurs logiques de même dimension que le tableau et on sélectionne ainsi que les éléments du tableau correspond à la valeur True de la condition. Ainsi pour des tableaux X et Y de même dimension , l’expression X[X>0] sélectionne uniquement les éléments de X positifs, et Y[X>0] sélectionne les éléments Y[i] de Y
correspondants aux éléments positifs de X, i.e. tels que X[i]>0.
Pour la position du minimum, on utilisera la fonction numpy argmin qui renvoie l’indice du minimum d’un tableau. A partir de l’indice, on déduit la position.
Déterminer à partir de l’affichage des tableaux X et Y , la valeur de \(\epsilon\) (i.e. t.q. la condition soit vérifiée par 2 valeurs uniquement) et la mettre dans une variable eps.
Écrire les instructions python permettant d’obtenir une première approximation les deux racines et de la position du minimum que l’on mettra respectivement dans les variables python
a1r1,a1r2eta1xm.Afficher les valeurs trouvées ce qui vous permet de vérifier votre algorithme par rapport au tracé de la fonction.
# première approximation
## BEGIN SOLUTION
xr = X[np.abs(Y)<3.e-2]
a1r1 = xr[0]
a1r2 = xr[1]
print("Racines: ",a1r1,a1r2)
ind_a1xm = np.argmin(Y)
a1xm = X[ind_a1xm]
print("Position du minimum: ",a1xm)
## END SOLUTION
Racines: -1.6 -1.52
Position du minimum: -1.52
# ne pas modifier
## BEGIN HIDDEN TESTS
assert(np.allclose([_x0_,_x1_],[a1r1,a1r2],atol=0.2))
assert(np.allclose((_x0_+_x1_)/2, a1xm, atol=0.2))
## END HIDDEN TESTS
4.4.4. Approximation numérique par dichotomie#
Pour obtenir une meilleure approximation numérique des racines on va utiliser un algorithme de dichotomie.
Principe algorithme dichotomie
Si on sait que sur un intervalle \([a,b]\), la fonction \(f(x)\) admet une racine unique \(x_r\) , une première approximation \(x_1\) est donnée par le milieu \(x_1 = (a+b)/2\).
On peut ensuite obtenir une nouvelle approximation en réduisant par deux la taille de l’intervalle en comparant le signe de \(f(x_1)\) avec le signe de \(f(a)\) et celui de \(f(b)\)
si \(f(x_1)\) a le même signe que \(f(a)\), remplacer \(a\) par \(x_1\)
sinon remplacer \(b\) par \(x_1\)
On répète ensuite tant que la longueur de l’intervalle \((b-a)<\epsilon\) où \(\epsilon\) est la précision souhaitée pour l’approximation :
Algorithme dichotomie
tant que (b-a)>eps
xm = (a+b)/2
si f(xm)*f(a) > 0 alors
a = xm
sinon
b = xm
fin boucle tant que
racine = (a+b)/2
Écrire la fonction python
dichotomieayant pour arguments la fonction f, les valeurs a,b etepsqui implémente cet algorithme et qui renvoieracinel’approximation de la racine de f(x) se trouvant dans l’intervalle \([a,b]\) avec une précisioneps.
On va utiliser la fonction dichotomie pour calculer une nouvelle approximation a2r1 et a2r2 des deux racines de F(x). On sait que la première racine se trouve entre -2.0 et la position du minimum a1xm et la seconde entre a1xm et 2.0. On choisit une précision de \(10^{-5}\)
Écrire les instructions python correspondantes et comparez avec les approximations précédentes.
# fonction dichotomie
## BEGIN SOLUTION
def dichotomie(f,a,b,eps):
while (b-a) > eps :
xm = (a+b)/2.
if f(xm)*f(a) > 0 :
a = xm
else :
b = xm
racine = (a+b)/2.
return racine
## END SOLUTION
# application
## BEGIN SOLUTION
xa = -2.
xb = a1xm
a2r1 = dichotomie(F,xa,xb,1.e-5)
xa = a1xm
xb = +2.
a2r2 = dichotomie(F,xa,xb,1.e-5)
print("approximation 2 des racines {:.6f} {:.6f}".format(a2r1,a2r2))
print("approximation 1 des racines {:.6f} {:.6f}".format(a1r1,a1r2))
## END SOLUTION
approximation 2 des racines -1.618683 -1.408298
approximation 1 des racines -1.600000 -1.520000
# ne pas modifier
## BEGIN HIDDEN TESTS
xa = -2.0; xb = (_x0_+_x1_)/2.
assert(np.allclose(dichotomie(F,xa,xb,1.e-5),_x0_,atol=1.e-2))
xa = xb; xb = 2.
assert(np.allclose(dichotomie(F,xa,xb,1.e-5),_x1_,atol=1.e-2))
## END HIDDEN TESTS
4.4.4.1. Algorithme de dichotomie pour le minimum#
On reprend l’idée de l’algorithme précédent pour l’appliquer à la recherche du minimum. On suppose que la fonction \(f(x)\) admet un minimum unique sur \([a,b]\) et que avant ce minimum la fonction est strictement décroissante, et après de minimum la fonction est strictement croissante.
Dans ce cas, une première approximation de la position de ce minimum est \(x_1 = (a+b)/2\) et on a
Pour déterminer un intervalle plus petit contenant ce minimum, il faut que la valeur au milieu de cet intervalle soit inférieur à la valeur aux extrémités. On va donc calculer la valeur en 2 points supplémentaires \(x_2\) et \(x_3\), milieu respectivement de \([a,x_1]\) et \([x_1,b]\). En comparant les valeurs en ces points, on en déduit un intervalle 2 fois plus petit.
Algorithme minimum
tant que (b-a) > eps
x1 = (a+b)/2
x2 = (a+x1)/2
x3 = (x1+b)/2
if f(x2)<f(a) et f(x2)<f(x1) alors
b = x1
sinon si f(x3)<f(x1) et f(x3)<f(b) alors
a = x1
sinon
a = x2
b = x3
fin boucle tant que
xmin = (a+b)/2
Écrire la fonction python
minimumayant pour arguments la fonction f, les valeurs a,b etepsqui implémente cet algorithme et qui renvoie l’approximation du minimum de f(x) se trouvant dans l’intervalle \([a,b]\) avec une précisioneps.
On va utiliser cette fonction pour calculer une nouvelle approximation
a2xm du minimum de F(x).
On sait que ce minimum se trouve entre les 2 racines et on choisit une précision de \(10^{-5}\)
Écrire le code python correspond et comparez avec les approximations précédentes.
# fonction minimum
## BEGIN SOLUTION
def minimum(f,a,b,eps):
while (b-a) > eps :
x1 = (a+b)/2.
x2 = (a+x1)/2.
x3 = (x1+b)/2.
if f(x2)<f(a) and f(x2)<f(x1):
b = x1
elif f(x3)<f(x1) and f(x3)<f(b):
a = x1
else :
a = x2
b = x3
return (a+b)/2.
## END SOLUTION
# application
# BEGIN SOLUTION
xa = a2r1
xb = a2r2
a2xm = minimum(F,xa,xb,1.e-5)
print("Approximation 2 du Minimum {:.6f}".format(a2xm))
print("Approximation 1 du Minimum {:.6f}".format(a1xm))
## END SOLUTION
Approximation 2 du Minimum -1.513487
Approximation 1 du Minimum -1.520000
# ne pas modifier
## BEGIN HIDDEN TESTS
xa = _x0_; xb = _x1_
assert(np.allclose(minimum(F,xa,xb,1.e-5),(_x0_+_x1_)/2.,atol=1.e-2))
## END HIDDEN TESTS
4.4.5. Approximation analytique par interpolation#
On sait que la fonction F(x) est un polynôme du second degré. On va donc numériquement calculer les coefficients du polynôme , puis utiliser les résultats analytiques sur les racines d’un polynôme et le minimum (point où la dérivée s’annule).
Si \(F(x) = a x^2 + b x + c\) , alors si on calcule la valeur de \(F(x)\) en 3 points distincts \(x_1,x_2,x_3\), on obtient un système linéaire de 3 équations à 3 inconnues \((a,b,c)\) qu’il suffit de résoudre numériquement pour obtenir les coefficients
On choisit comme points \(x_1=0, x_2=1 , x_3=2\)
Mettre dans une matrice numpy A les coefficients de la matrice du système linéaire et dans un vecteur numpy B les valeurs du 2nd membre.
Utiliser la fonction numpy : np.linalg.solve(A,B) pour résoudre le système linéaire \(A X = B\)
et en déduire la valeur des coefficients (a,b,c) que l’on mettra dans un vecteur numpy C.
## BEGIN SOLUTION
A = np.matrix([[0,0,1.],[1.,1.,1.],[4.,2.,1.]])
B = np.array([F(0.),F(1.),F(2.)])
C = np.linalg.solve(A,B)
print("coeffients du polynome:",C)
## END SOLUTION
coeffients du polynome: [1.88720601 5.71252686 4.30203722]
# ne pas modifier
## BEGIN HIDDEN TESTS
assert(np.allclose(A@C,B,atol=1e-8))
## END HIDDEN TESTS
Écrire une fonction poly2 qui prend pour argument le tableau
A des coefficients (a,b,c) d’un polynôme du second et la valeur de x
et qui renvoie la valeur du polynôme.
Utiliser cette fonction pour calculer le vecteur numpy Err contenant l’erreur (en valeur absolue) entre la fonction F(x) et ce polynôme pour les valeurs de x contenu dans X.
En déduire la valeur maximale de l’erreur pour valider le calcul.
On va maintenant utiliser cette interpolation (tableau des coefficients du polynôme de degré 2) pour calculer les valeurs des racines et du minimum à partir de formules analytiques.
Pour cela, écrire une fonction python racines qui, à partir du vecteur A des
coefficients du polynôme de degré 2, calcule le discriminant et renvoie les 2 racines réelles (si elles existent)
ou None sinon.
En utilisant cette fonction, calculez la valeur des 2 racines dans les variables r1,r2 et ensuite la position du minimum dans xm. Afficher les valeurs et comparer avec les approximations précédentes
# fonction poly2 et vérification
## BEGIN SOLUTION
def poly2(A,x):
return A[0]*x**2 + A[1]*x + A[2]
#
Err = np.abs(F(X) - poly2(C,X))
print("Erreur max: ", max(Err))
## END SOLUTION
# fonction racines
## BEGIN SOLUTION
def racines(A):
delta = A[1]**2 - 4*A[0]*A[2]
if delta < 0.0 :
return None
x1 = (-A[1]-np.sqrt(delta))/(2*A[0])
x2 = (-A[1]+np.sqrt(delta))/(2*A[0])
return x1,x2
## END SOLUTION
# application pour calcul des racines
## BEGIN SOLUTION
r1,r2 = racines(C)
print("racines : ",r1,r2)
print("approximation 2 racines: ",a2r1,a2r2)
print("approximation 1 racines: ",a1r1,a1r2)
xm = -C[1]/(2*C[0])
print("minimum en : ",xm)
print("approximation 2 minimum en : ",a2xm)
print("approximation 1 minimum en : ",a1xm)
## END SOLUTION
Erreur max: 1.1435297153639112e-14
racines : -1.6186805585951856 -1.4082952075809239
approximation 2 racines: -1.6186828613281252 -1.4082980346679688
approximation 1 racines: -1.6 -1.52
minimum en : -1.5134878830880547
approximation 2 minimum en : -1.5134872377803552
approximation 1 minimum en : -1.52
# ne pas modifier
## BEGIN HIDDEN TESTS
_r1_,_r2_ = racines(C)
if (_r1_ > _r2_): _r1_,_r2_ = _r2_,_r1_
assert(np.allclose([_r1_,_r2_],[_x0_,_x1_],atol=1.e-5))
assert(np.allclose([r1,r2,xm],[_x0_,_x1_,(_x0_+_x1_)/2.],atol=1.e-5))
## END HIDDEN TESTS
4.4.6. Conclusion#
Ecrire en markdown dans la cellule suivante une petite conclusion en classant les approches suivant leurs précisions et leurs généralités.
On a utilisé dans ce TP différentes approches pour calculer les racines et le minimum d’une fonction à partir de valeurs numériques de la fonction.
L’approche la plus simple consiste à calculer dans un tableau la valeur numérique de la fonction en des points équi-répartis sur l’intervalle d’étude. Puis, on détermine dans ce tableau les points les plus proches des racines et du minimum. C’est une méthode simple, générale, mais peu précise. Dans notre cas, la précision est de l’ordre de \(10^{-2}\).
La seconde approche utilise deux algorithmes de dichotomie, qui permettent d’affiner la solution. Les solutions obtenues sont plus précises. Dans notre cas, la précision est de l’ordre de $10^{-6}. Ce sont des méthodes itératives générales, mais qui peuvent être coûteuses en nombre d’itérations.
La dernière approche analytique consiste à utiliser une interpolation polynomiale. C’est la méthode la plus précise, mais elle suppose que la fonction est un polynôme dont on connaît le degré. Ce n’est donc pas une méthode générale.
