Équations différentielles ordinaires

Contenu

1. Équations différentielles ordinaires#

1.1. Définition d’une ODE#

Soit le système de n équations différentielles d’ordre 1

\[\begin{split}\begin{aligned} & & \frac{dY}{dt}=F(Y,t)\label{eq1}\\ & & Y(0)=Y_{0}\nonumber \end{aligned}\end{split}\]

$Y(t)$ $Y_{0}$ et $F(Y,t)$ sont des vecteurs de dimension n

Important

une EDO d’ordre N

\[y^{(n)}=f(y,y',y'',..,y^{(n-1)})\]

se transforme en un système de N EDO d’ordre 1 avec le changement de variables

\[Y1=y,\,Y2=y',\,Y_{3}=y'',..Y_{n}=y^{(n-1)}\]

le système à résoudre s’écrit alors:

(1.3)#\[\begin{eqnarray} Y_{1}'&=& Y_{2}\\ Y_{2}'&=& Y_{3}\\ \ldots &=& \ldots\\ Y_{n}'&=& f(Y_{1},Y_{2},..t) \end{eqnarray}\]

Nous rappelons ci-dessous les méthodes classiques d’approximation numérique pour la résolution d’EDO d’ordre 1.

1.2. Méthode d’Euler#

Approximation de Y(x) sur [a,b]

On subdivise l’intervalle [a,b], avec un pas d’intégration h :

\[h=\frac{b-a}{N}\]

on note $Y_{n}$ la solution approchée de $Y(x_{n})$
La suite $Y_{n}$ est obtenue par la relation de récurrence

Algorithme d’Euler

\[Y_{0}=Y(x_{0})\mbox{ donné}\]

pour n>0 :

\[Y_{n+1}=Y_{n}+hf(x_{n},Y_{n})\mbox{ pour }n>0\]

Analyse du schéma d’Euler

Interprétation graphique: ce schéma correspond à l’approximation de la courbe par sa tangente calculée en $x_n$
c’est un D.L. de $Y(x_{n+1})$ au voisinage de $Y(x_{n})$
c’est une approximation de $Y'(x_{i})$ par différences décentrées amont
c’est une méthode de base explicite à un pas d’ordre 1, donc très peu précise

1.3. Méthodes de Runge Kutta#

Classe de méthodes explicites d’ordre élevé à un pas, que l’on utilise à la place de la méthode d’Euler.

1.3.1. Méthode Runge Kutta d’ordre 2#

Utilisation d’une approximation de la tangente en $x_{n+1/2}$

Algorithme RK2

\[\begin{split}\begin{aligned} K_{1} & = & f(x_{n},Y_{n})\\ K_{2} & = & f(x_{n}+\frac{h}{2},Y_{n}+\frac{h}{2}K_{1})\\ Y_{n+1} & = & Y_{n}+hK_{2}\end{aligned}\end{split}\]

1.3.2. Méthode Runge Kutta d’ordre 4#

Utilisation d’une combinaison linéaire d’approximations de la tangente sur $[x_n,x_{n+1}]$

Algorithme RK4

\[\begin{split}\begin{aligned} K_{1} & = & f(x_{n},Y_{n})\\ K_{2} & = & f(x_{n}+\frac{h}{2},Y_{n}+\frac{h}{2}K_{1})\\ K_{3} & = & f(x_{n}+\frac{h}{2},Y_{n}+\frac{h}{2}K_{2})\\ K_{4} & = & f(x_{n}+\frac{h}{2},Y_{n}+hK_{3})\\ Y_{n+1} & = & Y_{n}+\frac{h}{6}(K_{1}+2K_{2}+2K_{3}+K_{4})\end{aligned}\end{split}\]

1.4. Méthode de Prédiction-Correction#

Ce sont des méthodes explicites couplées sur plusieurs pas en temps.

1.4.1. Méthodes d’Adams, Adams-Moulton#

On prédit une valeur $Y_{n+1}^{p}$ de $Y(t^{n+1})$ par extrapolation, puis on corrige cette valeur pour obtenir $Y_{n+1}=Y_{n+1}^{c}$:

Algorithme Adams Moulton

\[\begin{split}\begin{aligned} & & Y_{n+1}^{p}=Y_{n}+\frac{h}{12}(23F(Y_{n},t^{n})-16F(Y_{n-1},t^{n-1})+5F(Y_{n-2},t^{n-2})\\ & & Y_{n+1}^{c}=Y_{n}+\frac{h}{12}(5F(Y_{n+1}^{p},t^{n+1})+8F(Y_{n},t^{n})-F(Y_{n-1},t^{n-1}))\end{aligned}\end{split}\]

Ces méthodes à pas liés sont plus rapides que les méthodes à pas séparées (R.K.), mais on a un problème d’initialisation !

1.5. Problèmes raides#

Pour résoudre des problèmes raides, les méthodes explicites précédentes peuvent ne pas converger.

D’où l’utilisation de méthodes implicites avec un calcul du Jacobien de $F(Y,t)$

calcul implicite de $Y_{n+1}$

\[Y_{n+1}=Y_{n}+h*F(Y_{n+1},t^{n+1})\]

avec un calcul par Newton linéarisé de $F(Y_{n+1},t^{n+1})$

\[F(Y_{n+1},t^{n+1})=F(Y_{n},t^{n})+\frac{\partial F}{\partial Y}(Y_{n},t^{n})(Y_{n+1}-Y_{n})\]

d’où le calcul de $Y_{n+1}$ par résolution du système linéaire d’ordre n:

\[(Id-h*\frac{\partial F}{\partial Y}(Y_{n},t^{n}))(Y_{n+1}-Y_{n})=h*F(Y_{n},t^{n})\]

$Id$ est la matrice identité d’ordre n, et
$\frac{\partial F}{\partial Y}$ est la Jacobienne (matrice d’ordre n) de F

Calcule de la jacobienne $\frac{\partial F}{\partial Y}$

Calcul exacte de la Jacobienne

\[(\frac{\partial F}{\partial Y})_{i,j}=\frac{\partial F_{i}}{\partial Y_{j}}\]
Approximation numérique de la Jacobienne

\[(\frac{\partial F}{\partial Y})_{i,j}\approx\frac{F_{i}(Y_{1},..Y_{j}+dY_{j},..Y_{n})-F_{i}(Y_{1},..Y_{j},..Y_{n})}{dY_{j}}\]

Implémentation dans l”algorithme BDF (Backward Differentation Formula)

bibliothèque LSODA, SUNDIALS

1.6. Examples#

1.6.1. Utilisation de la méthode d’Euler#

soit l’EDO

\[\frac{dy}{dt}=y^{2}-t\mbox{ avec }y(0)=1\]

Le programme Python suivant permet le calcul de la solution approchée avec la méthode d’Euler

import numpy as np
def F(Y,t):
	return Y*Y-t

N   = 21
Tmax= 1
dt  = Tmax/(N-1)
T = np.linspace(0,Tmax,N)
Y = np.zeros(N)
Y[0]=1

for i in range(1,N):
       Y[i]=Y[i-1]+dt*F(Y[i-1],T[i-1])

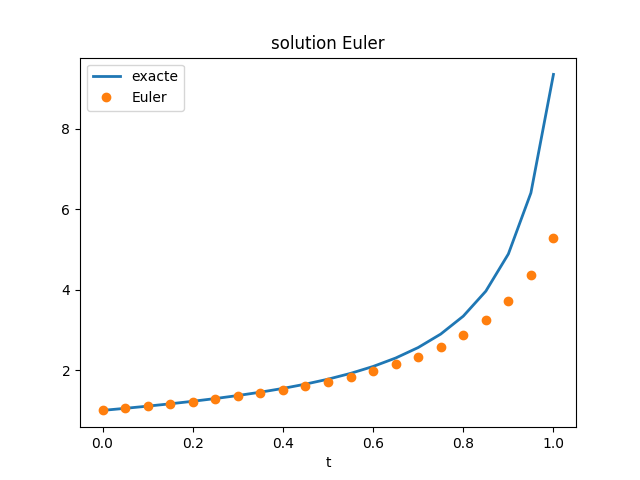
Sur la figure suivante, on compare cette solution numérique avec la solution exacte, et on constate que l’erreur augmente au cours du temps, ce qui est caractéristique de la méthode d’Euler.

solution numérique

1.6.2. Résolution du problème de Voltera#

Problème dynamique proies/prédateurs

À Trieste, pendant la première guerre mondiale, la pêche avait bien sûr diminué à cause des événements. La pêche consistait à lancer des filets et à récupérer tous les poissons. Le bureau des pêches avait constaté qu’alors la proportion de poissons du style requins, peu intéressants pour la consommation, avait considérablement augmenté par rapport aux poissons intéressants du style sardines. Ils demandèrent l’aide de Volterra qui modélisa le système requins-sardines

Modèle de Volterra

Voltera a proposé le modèle approché suivant, appelé aussi système de Lotka-Volterra (proie-prédateur). C’est un système de deux équations différentielles suivantes où $x(t)$ représente le nombre de sardines et $y(t)$ représente le nombre de requins.

\[\begin{split}\begin{aligned} & & \frac{dx}{dt}=ax(t)-bx(t)y(t)\mbox{ avec }a,b>0\\ & & \frac{dy}{dt}=cx(t)y(t)-dy(t)\mbox{ avec }c,d>0\\ \end{aligned}\end{split}\]

avec la condition initiale:

\[ x(0)=x_{0}\mbox{ et }y(0)=y_{0} \]

Ce modèle approché, appelé aussi système de Lotka-Volterra, signifie qu’en

l’absence de requins les sardines prolifèrent $x'(t)=a x(t)$, qu’en l’absence de sardines les requins disparaissent $y'(t)=-d y(t)$. Le terme en $x(t)y(t)$, qui représente la rencontre des requins et des sardines, augmente le nombre de requins et diminue le nombre de sardines (car ces dernières sont mangées par les requins).

L’objectif est de déterminer le point d’équilibre du système dynamique dans l’espace des phases. On peut facilement vérifier à partir des équations que ce point d’équilibre des populations correspond à :

\[ x = \frac{d}{c} \mbox{ et } y = \frac{a}{b} \]

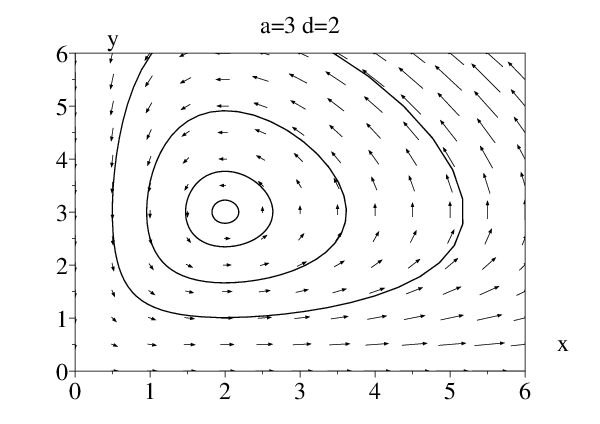
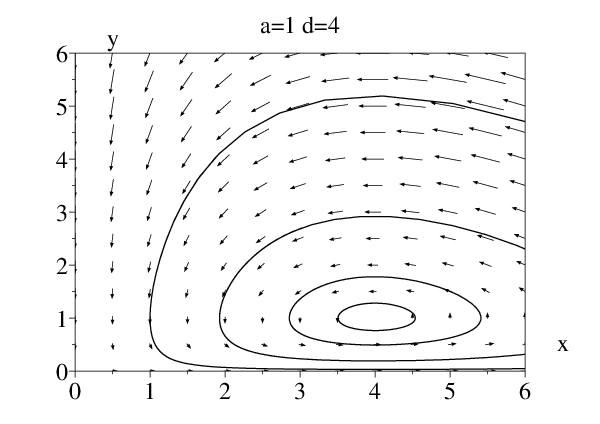
C’est ce que l’on vérifie pour les 2 séries de paramètres suivants, dont les simulations avec RK4 sont tracés sur les figures ci-dessous dans l’espace des phases:

a=3, b=1, c=1 et d=2

solution dans l'espace des phases

a=1, b=1, c=1 et d=4

solution dans l'espace des phases

1.6.3. Problème raide de réaction chimique#

On considère le problème de la réaction chimique de Robertson

\[\begin{split}\begin{aligned} & & y_{1}'=-0.04y_{1}+10^{4}y_{2}*y_{3}\\ & & y_{2}'=-y_{1}'-y_{3}'\\ & & y_{3}'=3.10^{7}y_{2}^{2}\end{aligned}\end{split}\]

Pour ce problème, les méthodes classiques de RK4, ADAMS ne convergent pas !!!

On doit utiliser une méthode implicite avec un calcul du Jacobien $J=\frac{\partial F}{\partial Y}$

1.6.4. Contrôle des CI: Faulkner Scan#

Problème de Faulkner Scan

L’équation de la couche limite laminaire en présence d’un gradient de pression externe (fonction de $\beta$) est régie par l’EDO suivante:

\[\frac{\partial^{3}f}{\partial\eta^{3}}+f(\eta)\frac{\partial^{2}f}{\partial\eta^{2}}+\beta(1-(\frac{\partial f}{\partial\eta})^{2})=0\]

avec les conditions aux limites:

\[f(0)=0,\frac{\partial f}{\partial\eta}(0)=0,f(\infty)=1\]

Le profil de vitesse est donné par

\[\frac{u}{u_{e}}=\frac{\partial f}{\partial\eta}\mbox{ avec }\eta=\frac{y}{\sqrt{2}}\frac{u_{e}}{\sqrt{(}\nu x)}\]

pour $\beta=0$ on retrouve l’équation de Blasius (couche limite sur plaque plane)

Problème de la C.I.

Pour résoudre l’EDO, on doit introduire une condition initiale supplémentaire:

\[\frac{\partial^{2}f}{\partial\eta^{2}}(0)=\alpha\]

où $\alpha$ doit être tel que la condition à l’infini soit vérifiée: $f(10)=1$ (on choisit $\infty=10$)

On se ramène donc à résoudre:

\[\frac{\partial^{3}f}{\partial\eta^{3}} + f(\eta)\frac{\partial^{2}f}{\partial\eta^{2}} + \beta (1-(\frac{\partial f}{\partial\eta})^{2})=0 \]

avec les conditions initiales

\[f(0)=0,\frac{\partial f}{\partial\eta}(0)=0,\frac{\partial^{2}f}{\partial\eta^{2}}(0)=\alpha\]

Pour résoudre ce problème on peut utiliser

une méthode de Tir,
une méthode des Adjoints,
une méthode de Continuation.

1.6.4.1. méthode de continuation SCILAB#

cas équation de Blasius $\beta=0$

1.6.4.2. méthode de Tir#

On part d’une solution $f_{\alpha_{0}}$ calculée pour $\alpha=\alpha_{0}$ et on corrige la solution en calculant la correction $df(\eta)$ connaissant $f_{\alpha_{0}}$ par résolution du problème de gradient (i.e. calcul de la variation $df$ de la solution pour une variation $d\alpha=1$ de la C.L. $\frac{\partial^{2}f}{\partial\eta^{2}}(0)=\alpha$)

\[\frac{\partial^{3}df}{\partial\eta^{3}}+f_{\alpha_{0}}(\eta)\frac{\partial^{2}df}{\partial\eta^{2}}+df(\eta)\frac{\partial^{2}f_{\alpha_{0}}}{\partial\eta^{2}}-2\beta\frac{\partial df}{\partial\eta}\frac{\partial f_{\alpha_{0}}}{\partial\eta}=0\label{eqkscan1}\]

avec les conditions aux limites

\[df(0)=0,\frac{\partial df}{\partial\eta}(0)=0,\frac{\partial^{2}df}{\partial\eta^{2}}(0)=1\]

Etape de correction

En utilisant la méthode de Newton, on obtiens la correction recherchée sur $\alpha$

\[\alpha_{1}=\alpha_{0}-\frac{f_{\alpha_{0}}(10)-1}{df(10)}\]

Tant que $\left\Vert f_{k}(10)-1\right\Vert \ge\varepsilon$
calcul $df_{k}(\eta)$ connaissant $f_{k}(\eta)$ par résolution de ([eqkscan1]{reference-type= »ref » reference= »eqkscan1 »})
calcul de la nouvelle valeur $\alpha_{k}$ $$\alpha_{k+1}=\alpha_{k}-\frac{f_{k}(10)-1}{df_{k}(10)}$$
calcul de $f_{k+1}(\eta)$par résolution de ([eqkskan]{reference-type= »ref » reference= »eqkskan »})

Méthode de tir SCILAB

cas équation de Blasius $\beta=0$

[Execution blasiustir.sce]{lang= »en-« }

cas Faulkner Scan $\beta=-0.1..0.1$

[Execution Scilab faulknerskan]{lang= »en-« }

1.7. Résolution d’équations sous contraintes: DAE#

DAE: Équations Différentielles Algébriques

sous forme implicites

\[g(t,Y,Y')=0\mbox{ avec }Y(0)=Y_{0}\]
sous la forme d’un problème sous contraintes:

\[\begin{split}\begin{aligned} & & \dot{y}=f(y,u)\\ & & 0=g(y,u)\end{aligned}\end{split}\]

Problème sous contrainte

Problèmes de mécanique sous contrainte: équations de Lagrange pour n variables $q_{k}$

\[\begin{split}\begin{aligned} & & \frac{d}{dt}(\frac{\partial L}{\partial\dot{q_{k}}})-\frac{\partial L}{\partial q_{k}}=0,\mbox{ pour }k=0,..,n\\ & & 0=g(q)\end{aligned}\end{split}\]

ou $g(q)$ est un vecteur de m contraintes

Problème de minimisation du Lagrangien $L(\dot{q}_{k},q_{k})$ sous la contrainte $g(q)=0$.
Elimination des contraintes $\leadsto$$n-m$ inconnues indépendantes
[pas toujours possible !]{style= »color: red »}

1.7.1. Un exemple classique: le problème du laitier#

Un laitier doit se rendre d’un point $M$ (la laiterie) à un point $C$ (la ferme) pour chercher le lait. Il doit cependant s’arrêter près de la rivière (courbe $g(x,y)=0$). Quel est le trajet le plus court pour aller de $M$ à $C$ en passant par un point de la courbe $g(x,y)=0$?

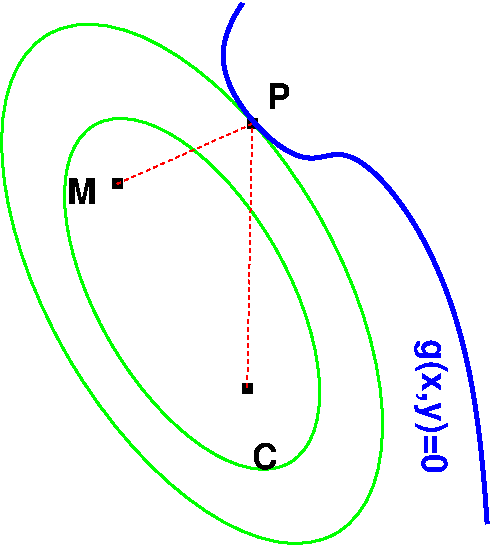
Ce qui est équivalent à déterminer le point $P$ de la courbe $g(x,y)=0$ tel que la distance $\left\Vert \overrightarrow{MP}\right\Vert +\left\Vert \overrightarrow{PC}\right\Vert$ soit la plus petite possible. Soit, mathématiquement:

Trouvez le point $P$ tel que $f(P)=\left\Vert \overrightarrow{MP}\right\Vert +\left\Vert \overrightarrow{PC}\right\Vert$ soit minimum sous la contrainte $g(P)=0$

Ce problème admet une solution graphique: on trace les ellipses de foyers $M$ et $C$. Chaque ellipse correspond à une courbe $f(P)=cste$ (la distance d’un point d’une ellipse aux foyers est constance puisqu’on trace une ellipse avec une corde et 2 piquets). Le point $P$ recherché correspond à l’intersection de la plus petite ellipse tangente à la courbe $g(x,y)=0$.

Mathématiquement, on écrit qu’en $P$ la tangente à l’ellipse $f(P)=cste$ est parallèle à la tangente à la courbe $g(P)=0$. Ces deux vecteurs sont parallèles si:

\[\overrightarrow{grad}\,f(P)\,=\lambda\,\overrightarrow{grad}\,g(P)\]

où $\lambda$ est le multiplicateur de Lagrange associé à la contrainte

On résout le système de 3 inconnues $(x,y,\lambda)$:

(1.4)#\[\begin{eqnarray} \overrightarrow{grad}\,f(P) &=& \lambda\,\overrightarrow{grad}\,g(P)\\ g(P) &=& 0 \end{eqnarray}\]

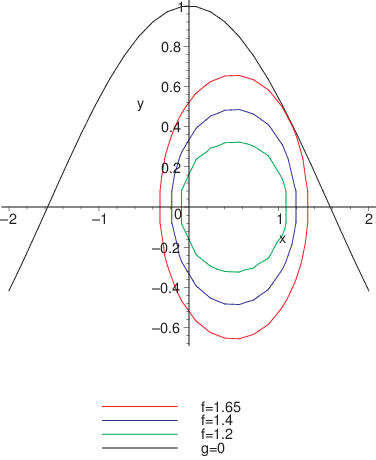
Par exemple, pour $M=(0,0)$, $C=(1,0)$ et $g(P)=y-cos(x)$, la solution s’écrit:

\[x=1.119,\,y=0.436,\,\lambda=1.654\]

et correspond à l’ellipse $f(x,y)=1.654$

1.7.2. Condition de minimisation sous contrainte#

De façon générale, la condition de minimisation d’une fonction $f$ sous contrainte $g=0$ impose que le gradient de la fonction à minimiser $f(X)$ soit parallèle au gradient de la contrainte $g(X)=0$:

\[\begin{split}\begin{aligned} \overrightarrow{\nabla_{X}}f & = & \lambda\overrightarrow{\nabla_{X}}g\nonumber \\ g(X) & = & 0\end{aligned}\end{split}\]

: La méthode des multiplicateurs de Lagrange

La relation [c2eq2]{reference-type= »ref » reference= »c2eq2 »} et l’équation de la contrainte peut aussi s’interpréter comme la condition de minimisation de la fonctionnelle $F(X,\lambda)$ de $X$ et $\lambda$ suivante:

\[F(X,\lambda)=f(X)-\lambda g(X)\]

dont le gradient vaut:

\[\begin{split}\begin{aligned} \overrightarrow{\nabla_{X}}F & = & \overrightarrow{\nabla_{X}}f-\lambda\overrightarrow{\nabla_{X}}g \\ \overrightarrow{\nabla_{\lambda}}F & = & -g(X)\end{aligned}\end{split}\]

La condition de minimisation de $F(X,\lambda)$ équivaut donc aux équations

1.7.3. Multiplicateurs de Lagrange#

Aux m contraintes, on associe m multiplicateurs $\lambda_{i}$
On définit un nouveau lagrangien

\[L(q,\dot{q},\lambda)=T(q,\dot{q})-U(q,\dot{q})-\sum_{i=1}^{m}{\lambda_{i}g_{i}(q)}\]

Les équations de Lagrange avec $n+m$ inconnues $\{q,\lambda\}$\

(1.5)#\[\begin{eqnarray} \frac{d}{dt}\frac{\partial L}{\partial\dot{q}_{k}}-\frac{\partial L}{\partial q_{k}} &=& \sum_{i=1}^{m}{\lambda_{i}\frac{\partial g_{i}}{\partial q_{k}}(q)}\\ 0 &= & g_{i}(q)\end{eqnarray}\]

1.7.4. Forme du système différentielle algébrique#

On écrit donc le système différentielle algébrique sous la forme:

(1.6)#\[\begin{eqnarray} \dot{y}&=&f(y,u)\\ 0&=&g(y,u)\end{eqnarray}\]

$y$ est le vecteur d’état (degrés de liberté) de dimension $n$ du système décrit par le système de $n$ équations différentielles et $u$ le vecteur des $m$ multiplicateurs de Lagrange associé aux $m$ contraintes

Ce système d’écrit sous la forme matricielle

\[M(t,Y)\,\frac{dY}{dt}=F(Y,t)\]

$Y=\{y,u\}$ est le vecteur des $n+m$ inconnues, et $M(t,Y)$ est une matrice de masse singulière

1.7.5. Index d’une DAE#

Index d’une DAE: nombre de différenciations permettant d’obtenir une EDO

DAE d’Index 1:
si g dépend explicitement de u, on différencie $g$ pour obtenir une EDO : $\frac{dg}{dt}=\frac{\partial g}{\partial u}\frac{du}{dt}+\frac{\partial g}{\partial y}\frac{dy}{dt}=0$

\[\begin{split}\begin{aligned} & & \dot{y}=f(y,u)\\ & & \dot{u}=-(\frac{\partial g}{\partial u})^{-1}(\frac{\partial g}{\partial y})f(y,u)\end{aligned}\end{split}\]

DAE d’Index 2:
si g ne dépend pas de u, il faut différentier 2 fois pour obtenir une EDO, i.e. $\dot{g}(y)=0$ et $\ddot{g}(y)=0$

\[\begin{split}\begin{aligned} & & 0=(\frac{\partial g}{\partial y})f(y,u)\\ & & \dot{u}=-(g_{y}(y)f_{u}(y,u))^{-1}(g_{yy}(y)f(y,u)*f(y,u)+g_{y}(u)f_{y}(y,u))\end{aligned}\end{split}\]

Attention on utiise des notations vectorielles

1.7.6. DAE avec Python#

Matlab peut résoudre les DAE d’ordre 1 de la forme

\[M(t,Y)\,\frac{dY}{dt}=F(t,Y)\]

où $M(t,Y)$ est une matrice éventuellement singulière.

Les solveurs explicites (non stiff) ne sont pas utilisables (Runge Kutta ode23, ode45, Adams Bashford ode113)
Les solveurs implicites (stiff) utilisables sont les fonctions matlab: BDF
ode15s et RK implicite ode23s
La matrice $M$ est définie avec la fonction odeset
options=odeset(“Mass”,M);
La condition initiale doit etre compatible ! (i.e. vérifier la contrainte!)

1.7.7. Solveurs numériques#

BDF= Backward Differentiation Formula
NDF= variante Numerical Differentiation Formula (utilisé dans Matlab)

Principe:

on calcule le pôlynome d’interpolation $P_{k}(t)$ de degré $k$ passant par les points $Y_{n+1},Y_{n},..Y_{n-k+1}$ et on discrétise l’équation de façon implicite avec le schéma DBF d’ordre k:

\[M(t^{n+1})P_{k}'(t)=F(Y^{n+1},t^{n+1})\]

Pour un schéma d’ordre $k=1$, $P_{1}(t)=(Y^{n+1}-Y^{n})*(t-t^{n})/dt\,+\,Y^{n}$, d’où

\[\frac{1}{dt}M(t^{n+1})(Y^{n+1}-Y^{n})=F(Y^{n+1})\]

résolution par itérations de Newton (avec $Y_{0}^{n+1}\sim Y^{n+1}$)

\[\left(\frac{1}{dt}M(t^{n+1})-\frac{\partial F}{\partial Y}(Y_{0}^{n+1})\right)\left(Y^{n+1}-Y^{n}\right)=F(Y^{n})\]

Même si $M$ est singulière, on peut encore résoudre

1.7.8. Exemple 1: pendule simple en cartésien#

Mouvement du pendule = équation de Lagrange en variables $[x,y]$

Lagrangien $$L=\frac{1}{2}m(\dot{x}^{2}+y^{2})+mgy$$
Contrainte $$x^{2}+y^{2}=l^{2}$$
Lagrangien augmenté

\[L=\frac{1}{2}m(\dot{x}^{2}+y^{2})+mgy+\lambda(x^{2}+y^{2}-l^{2})\]

Equations de Lagrange

Problème initiale: DAE d’ordre 2

\[m\ddot{x}=-2\lambda x\]

\[m\ddot{y}+mgy=-2\lambda y\]

\[0=x^{2}+y^{2}-l^{2}\]

Transformation en DAE d’ordre 1, mais d’index 2

\[\begin{split}\left[\begin{array}{ccccc} m\\ & m\\ & & 1\\ & & & 1\\ & & & & 0 \end{array}\right]\dot{\left[\begin{array}{c} u\\ v\\ x\\ y\\ \lambda \end{array}\right]}=\left[\begin{array}{c} -2\lambda x\\ -2\lambda y-mg\\ u\\ v\\ x^{2}+y^{2}-l^{2} \end{array}\right]\end{split}\]

Transformation en DAE d’index 1

Transformation en DAE d’index 1
Dérivation de la contrainte 2 fois:
$x^{2}+y^{2}-l^{2}=0$ $\leadsto$$xu+yv=0$$\leadsto$$u^{2}+v^{2}+x\dot{u}+y\dot{v}=0$

et on utilise l’équation pour remplacer $\dot{u}$ et $\dot{v}$ $\leadsto u^{2}+v^{2}-2\lambda(x^{2}+y^{2})-gy=0$ avec $x^{2}+y^{2}=1$

\[\begin{split}\left[\begin{array}{ccccc} m & & & & 0\\ & m & & & 0\\ & & 1 & & 0\\ & & & 1 & 0\\ 0 & 0 & 0 & 0 & 0 \end{array}\right]\dot{\left[\begin{array}{c} u\\ v\\ x\\ y\\ \lambda \end{array}\right]}=\left[\begin{array}{c} -2\lambda x\\ -2\lambda y-mg\\ u\\ v\\ u^{2}+v^{2}-2\lambda-gy \end{array}\right]\end{split}\]

Programme

Résolution avec une matrice $M$ singulière et ode15s

Pénalisation

Problème: la contrainte $g(x,y)=0$ n’est plus très bien satisfaite numériquement
Solution: pénalisation de la dernière relation

On résout le système:

\[\ddot{g}(x,y)+2\alpha\beta\dot{g}(x,y)+\beta^{2}g(x,y)=0\]

par analogie avec un système masse ressort avec frottement:

\[\ddot{x}+2\alpha\beta\dot{x}+\beta^{2}x=0\]

le sytème revient à l’équilibre le plus rapidement pour $\alpha>0$
$\beta=\frac{2\pi}{T}$ donne l’échelle de temps pour ce retour (en mécanique $\beta\approx10$ pour avoir $T\approx1$)
valeurs courantes (Baumgard) $\alpha\approx 1$ et $\beta\approx 10\alpha$
Attention: la condition initiale sur $\lambda$ doit être compatible

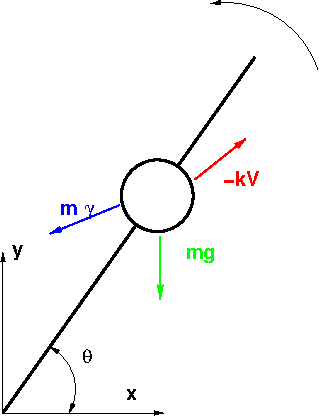
1.7.9. Exemple 2: perle sur une aiguille en rotation#

Calcul de la trajectoire d’une perle sur une aiguille en rotation uniforme.