TP Algorithmes en Python

Contenu

8.2. TP Algorithmes en Python#

cours Méthodes numériques avancées master M2 Mécanique

%matplotlib inline
# bibliotheque
import os,sys
import numpy as np
import matplotlib.pyplot as plt
import random
from validation.validation import info_etudiant, check_function, liste_functions, info_function
from IPython.display import Markdown, display
def printmd(string):
    display(Markdown(string))
#
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None 
# test si numero étudiant spécifier
if type(NUMERO_ETUDIANT) is not int :
    printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
    NOM,PRENOM,NUMERO_ETUDIANT = info_etudiant()
# parametres spécifiques
_uid_    = NUMERO_ETUDIANT 
_precis_ = 1.0e-5
_a_ = sum([int(c) for c in str(_uid_)])
printmd("**Etudiant {} {}  id={}**".format(NOM,PRENOM,NUMERO_ETUDIANT))

8.2.1. Algorithme 1: enveloppe convexe#

wikipedia

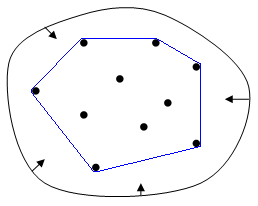
L’enveloppe convexe d’un objet ou d’un regroupement d’objets géométriques est l’ensemble convexe le plus petit parmi ceux qui le contiennent.

Dans un plan, l’enveloppe convexe peut être comparée à la région limitée par un élastique qui englobe tous les points qu’on relâche jusqu’à ce qu’il se contracte au maximum. L’idée serait la même dans l’espace avec un ballon qui se dégonflerait jusqu’à être en contact avec tous les points qui sont à la surface de l’enveloppe convexe.

8.2.1.1. Analyse du problème#

représentation des données
algorithme / mise en oeuvre

8.2.1.2. structure de données#

P variable Point: données avec un label num (chaîne de caractère) et des coordonnée (x,y)

P.label, P.x, P.y

8.2.1.2.1. implémentation python (classe / structure)#

class Point():

   def __init__(self,num,x,y):
      self.label = str(num)
      self.x = x
      self.y = y
      return

8.2.1.3. Algorithme#

principe:

on se ramène à un problème plus simple dont on connaît la solution
à quelle condition 3 points ABC font partie d’une enveloppe convexe
trie des points suivants x
parcours de la liste triée, et élimination successive des points qui ne vérifie pas le test précédent pour obtenir la première partie supérieure de la frontière convexe.
Refaire le parcours dans l’ordre inverse pour obtenir la seconde partie inférieure.

fonctions utiles

classe Point (avec label et coordonnées)
liste de Points
génération d’une liste de n points aléatoires dans un rectangle: liste_points
tracé des points avec leur label (avec le cas du tracer de la frontière) plot_points
trie de la liste des points suivant x trie_points
test 3 points ABC sont convexes: test_convexe
fonction frontiere_convexe

8.2.1.4. Implémentation Python#

# structure de données
class Point():
## BEGIN SOLUTION
## END SOLUTION

# verification
P1 = Point(1,0.2,0.5)
print("P1=",P1.label,P1.x,P1.y)

import random
def liste_points(n):
    """generation d'une liste de n points aléatoire dans une boite [b,3-b]x[b,2-b]"""
    b = 0.05 
    L = []
    for i in range(n):
        L.append(Point(i+1,random.uniform(b,3-b), random.uniform(b,2-b))) 
    return L

def plot_points(points,style='ro'): 
    """tracer de la liste des points avec les labels avec un style par defaut."""
    for pts in points:
            plt.text(pts.x, pts.y, '  '+pts.label)
    plt.plot([p.x for p in points], [p.y for p in points],style, linewidth=2.5)
    plt.axis('scaled'); plt.axis('off')
    return

# validation: exemple d'utilisation
Pts = liste_points(10)
plt.figure(figsize=(10,8))
plot_points(Pts)

# fonction pour trie une liste
def trie_points(Pts):
    """trie la liste des pts"""
## BEGIN SOLUTION
## END SOLUTION

# verification
PtsTries = trie_points(Pts)
for pt in PtsTries:
    print(pt.label,pt.x)

8.2.1.5. fonction test frontière convexe#

Écrire une fonction qui détermine si 3 points A,B,C forment une frontière convexe ABC

def test_convexe(A,B,C):
    """test si les 3 pts sont convexes"""
## BEGIN SOLUTION
## END SOLUTION

# verification
## BEGIN SOLUTION
## END SOLUTION

8.2.1.6. Algorithme frontiere convexe#

expliciter l’algorithme et sa validation
puis écrire une fonction frontiere_convexe qui renvoie la frontière convexe d’une liste de points

8.2.1.6.1. Algorithme (2 pts)#

=== BEGIN ANSWER ===

=== END ANSWER ===

# implementation
def frontiere_convexe(Pts):
    """renvoie la frontiere convexe de la liste de points Pts"""
## BEGIN SOLUTION
## END SOLUTION

# validation
Pts = liste_points(10)
Frontiere = frontiere_convexe(Pts)
plt.figure(figsize=(10,8))
plot_points(Pts)
plot_points(Frontiere,'-bx')

8.2.2. Algorithme 2 (optionnel) : problème du voyageur de commerce#

wikipedia: En informatique, le problème du voyageur de commerce est un problème d’optimisation qui, étant donné une liste de villes, et des distances entre toutes les paires de villes2, détermine un plus court chemin qui visite chaque ville une et une seule fois et qui termine dans la ville de départ.

Malgré la simplicité de son énoncé, il s’agit d’un problème d’optimisation pour lequel on ne connait pas d’algorithme permettant de trouver une solution exacte rapidement dans tous les cas.

C’est un problème algorithmique célèbre, qui a généré beaucoup de recherches et qui est souvent utilisé comme introduction à l’algorithmique ou à la théorie de la complexité. Il présente de nombreuses applications que ce soit en planification et en logistique, ou bien dans des domaines plus éloignés comme la génétique (en remplaçant les villes par des gènes et la distance par la similarité).

Comprenons-nous assez bien l’énoncé du problème pour programmer une solution

Étant donné un ensemble de villes:

Un ensemble Python pourrait représenter un ensemble de villes. Une ville individuelle peut être simplement un index entier ou des coordonnées (x, y).
… et la distance entre chaque paire de villes:

Nous pourrions utiliser une fonction, une distance (A, B) ou une table, la distance [A, B].
… quelle est la tournée la plus courte possible:

Un tour est un ordre séquentiel dans lequel visiter les villes; une fonction shortest_tour (tours) devrait trouver celle qui minimise tour_length (tour), qui est la somme des distances entre les villes adjacentes dans le tour.
… qui visite chaque ville une fois et retourne à la ville de départ:

Assurez-vous qu’une visite ne revienne pas dans une ville (sauf si vous revenez au départ).

## generation des villes
def Cities(n, width=999, height=666, seed=_uid_):
    "Make a set of n cities, sampled uniformly from a (width x height) rectangle."
    return [[random.randint(1, width), random.randint(1, height)]
                     for c in range(n)]

## generation d'un test pour 9 villes
C = Cities(9)
plt.figure(figsize=(10,8))
for k in range(len(C)):
    print("ville {} : position {}".format(k,C[k]))
    plt.plot([C[k][0]],[C[k][1]],'-o')
    plt.text(C[k][0], C[k][1], '  '+str(k))

8.2.2.1. Algorithme force brute#

Ecrire un algorithme calculant tous les trajets possibles et déterminant ensuite le minimum

# implemntation de l'algorithme (2 pts)
## BEGIN SOLUTION
## END SOLUTION

8.2.2.2. Optimisation#

Parmis les n! tours possibles, beaucoup sont équivalentd:

pour n=3 , (1,2,3) (2,3,1) (3,1,2) sont equivalents

8.2.2.3. Strategies#

Choisir une ou plusieurs stratégies parmis les stratégies suivantes pour optimiser votre algorithme

Brute Force Strategy:

The strategy used for exhaustive_tsp; as Ken Thompson says, « when in doubt, use brute force. »
Approximation Strategy:

If it is too hard to find a precise, optimal solution, consider finding an approximate, suboptimal solution.
Greeedy Strategy:

To complete a multiple step problem, first do the step that has the best gain. Repeat.
Iterative Improvement Strategy:

Use an existing algorithm to create a solution, then have another algorithm improve the solution.
Ensemble Strategy:

Apply a set of algorithms to the problem, and pick the best solution.
Divide and Conquer Strategy:

Split the problem in half, solve each half, and combine the two partial solutions.
Stand on the Shoulders of Giants Strategy:

Find out what other people have done, and copy (or modify).