5.2. TP OUTPUT DAE : pendule sur une courbe#
Marc BUFFAT dpt mécanique, Université Lyon 1
vous devez écrire les fonctions dont le nom est fixé, mais dont vous devez spécifier les arguments en fonction de la question posée.
Chaque fonction validée rapporte des points
Attention: executer toutes les cellules depuis le début en utilisant le bouton run
ERREUR: numéro d’étudiant non spécifié!!!
Login étudiant Marc BUFFAT uid=137764122
Parametres: m=2.7 M=6.55 l=2.81 a0=0.5
5.2.1. Pendule sur une courbe#

5.2.1.1. modélisation#
Les coordonnées du système sont \(Q=[x(t),y(t),\theta(t)]\), (coordonnées de m et angle de rotation du pendule). Le lagrangien du système est \(L(Q,\dot{Q},t)\) , et les équations de Lagrange sous contrainte s’écrivent
où le vecteur \(\vec{H}\) représente la contribution du travail \(\vec{H}.\delta\vec{Q}\) de la force de frottement \(\vec{F}\), \(\lambda\) le multiplicateur de Lagrange (i.e. la force de liaison) associé à la contrainte \(f(x,y)=0\), et \(\vec{G}\) la contribution due travail de cette force de liaison \(\lambda\vec{G}.\delta\vec{Q}\). $\( G_i = \frac{\partial f}{\partial Q_i}\)$
La courbe \(f(x,y)=0\) est le chameau \(y=x^{2}+a_0\cos(\omega x)\)
A l’instant initial le pendule se trouve la courbe en \(x_0, y_0=f(x_0)\) et on le lâche sans vitesse initiale avec un angle \(\theta=0\). On cherche à déterminer la position d’équilibre du système en fonction de \(x_{0}\).
5.2.1.2. Définition des repères et des points#
un référenciel R0 et un point O de référence:
système de deux points:
Q(xp,yp) de masse M glissant sur la courbe auquel est accroché l’autre point P
P distant de l de Q
“VP=”
\(\displaystyle \frac{d}{d t} x{\left(t \right)}\mathbf{\hat{r_0}_x} + \frac{d}{d t} y{\left(t \right)}\mathbf{\hat{r_0}_y}\)
'VQ='
\(\displaystyle (l \cos{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)} + \frac{d}{d t} x{\left(t \right)})\mathbf{\hat{r_0}_x} + (l \sin{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)} + \frac{d}{d t} y{\left(t \right)})\mathbf{\hat{r_0}_y}\)
\(\displaystyle g m y{\left(t \right)}\)
\(\displaystyle \frac{m \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}}{2} + \frac{m \left(\frac{d}{d t} y{\left(t \right)}\right)^{2}}{2}\)
\(\displaystyle M g \left(- l \cos{\left(\theta{\left(t \right)} \right)} + y{\left(t \right)}\right)\)
\(\displaystyle \frac{M \left(l \sin{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)} + \frac{d}{d t} y{\left(t \right)}\right)^{2}}{2} + \frac{M \left(l \cos{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)} + \frac{d}{d t} x{\left(t \right)}\right)^{2}}{2}\)
5.2.1.3. Calcul du lagrangien#
'L='
\(\displaystyle - M g \left(- l \cos{\left(\theta{\left(t \right)} \right)} + y{\left(t \right)}\right) + \frac{M \left(l \sin{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)} + \frac{d}{d t} y{\left(t \right)}\right)^{2}}{2} + \frac{M \left(l \cos{\left(\theta{\left(t \right)} \right)} \frac{d}{d t} \theta{\left(t \right)} + \frac{d}{d t} x{\left(t \right)}\right)^{2}}{2} - g m y{\left(t \right)} + \frac{m \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}}{2} + \frac{m \left(\frac{d}{d t} y{\left(t \right)}\right)^{2}}{2}\)
'contrainte='
\(\displaystyle - a_{0} \cos{\left(\omega x{\left(t \right)} \right)} - x^{2}{\left(t \right)} + y{\left(t \right)}\)
'Force de frottement='
[(P, - K*Derivative(x(t), t)*R_0.x - K*Derivative(y(t), t)*R_0.y)]
5.2.2. Bilan des équation#
Énergie cinétique
Énergie potentielle
Lagrangien
Force de frottement généralisée
contrainte $\( f(x,y) = y-(x^{2}+a_0\cos\omega x)\)$
gradient de la contrainte $\( G = \left[\begin{array}{c} \frac{\partial f}{\partial x}\\ \frac{\partial f}{\partial y}\\ 0 \end{array}\right]\)$
Ecrire les équations du mouvement, et les transformer en un système d’ordre 1 de la forme:
avec
on dérivera la contrainte autant de fois que nécessaire pour pouvoir résoudre.
\(\displaystyle \left[\begin{matrix}K \frac{d}{d t} x{\left(t \right)} + \frac{M \left(- 2 l \sin{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} + 2 l \cos{\left(\theta{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \theta{\left(t \right)} + 2 \frac{d^{2}}{d t^{2}} x{\left(t \right)}\right)}{2} + m \frac{d^{2}}{d t^{2}} x{\left(t \right)} - \left(- a_{0} \omega \sin{\left(\omega x{\left(t \right)} \right)} + 2 x{\left(t \right)}\right) \operatorname{lam}_{1}{\left(t \right)}\\K \frac{d}{d t} y{\left(t \right)} + M g + \frac{M \left(2 l \sin{\left(\theta{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \theta{\left(t \right)} + 2 l \cos{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} + 2 \frac{d^{2}}{d t^{2}} y{\left(t \right)}\right)}{2} + g m + m \frac{d^{2}}{d t^{2}} y{\left(t \right)} + \operatorname{lam}_{1}{\left(t \right)}\\M g l \sin{\left(\theta{\left(t \right)} \right)} + M l \left(- l \sin{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} + l \cos{\left(\theta{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \theta{\left(t \right)} + \frac{d^{2}}{d t^{2}} x{\left(t \right)}\right) \cos{\left(\theta{\left(t \right)} \right)} + M l \left(l \sin{\left(\theta{\left(t \right)} \right)} \frac{d^{2}}{d t^{2}} \theta{\left(t \right)} + l \cos{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} + \frac{d^{2}}{d t^{2}} y{\left(t \right)}\right) \sin{\left(\theta{\left(t \right)} \right)}\end{matrix}\right]\)
5.2.2.1. Mise sous forme matricielle#
\(\displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & M + m & 0 & M l \cos{\left(\theta{\left(t \right)} \right)} & - a_{0} \omega \sin{\left(\omega x{\left(t \right)} \right)} + 2 x{\left(t \right)}\\0 & 0 & 0 & 0 & M + m & M l \sin{\left(\theta{\left(t \right)} \right)} & -1\\0 & 0 & 0 & M l \cos{\left(\theta{\left(t \right)} \right)} & M l \sin{\left(\theta{\left(t \right)} \right)} & M l^{2} \sin^{2}{\left(\theta{\left(t \right)} \right)} + M l^{2} \cos^{2}{\left(\theta{\left(t \right)} \right)} & 0\\0 & 0 & 0 & a_{0} \omega \sin{\left(\omega x{\left(t \right)} \right)} - 2 x{\left(t \right)} & 1 & 0 & 0\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}\frac{d}{d t} x{\left(t \right)}\\\frac{d}{d t} y{\left(t \right)}\\\frac{d}{d t} \theta{\left(t \right)}\\- K \frac{d}{d t} x{\left(t \right)} + M l \sin{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2}\\- K \frac{d}{d t} y{\left(t \right)} - M g - M l \cos{\left(\theta{\left(t \right)} \right)} \left(\frac{d}{d t} \theta{\left(t \right)}\right)^{2} - g m\\- M g l \sin{\left(\theta{\left(t \right)} \right)}\\- a_{0} \omega^{2} \cos{\left(\omega x{\left(t \right)} \right)} \left(\frac{d}{d t} x{\left(t \right)}\right)^{2} + 2 \left(\frac{d}{d t} x{\left(t \right)}\right)^{2}\end{matrix}\right]\)
5.2.2.2. linéarisation#
pour des cooordonnées \(q\) et des vitesses généralisées \(u\), dont \(q_i\) et \(u_i\) sont indépendantes et \(r\) un forcage externe
\begin{split}M \begin{bmatrix} \delta \dot{q} \ \delta \dot{u} \ \delta \lambda \end{bmatrix} = A \begin{bmatrix} \delta q_i \ \delta u_i \end{bmatrix} + B \begin{bmatrix} \delta r \end{bmatrix}\end{split}
0 a0
\(\displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & 0 & 1 & 0 & 0\\0 & 0 & 0 & M + m & 0 & M l & 0\\0 & 0 & 0 & 0 & M + m & 0 & 1\\0 & 0 & 0 & M l & 0 & M l^{2} & 0\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}0 & 0 & 1 & 0\\0 & 0 & 0 & 0\\0 & 0 & 0 & 1\\0 & 0 & 0 & 0\\\left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right) & 0 & - K & 0\\0 & 0 & 0 & 0\\0 & - M g l & 0 & 0\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}0\\\frac{d}{d t} y{\left(t \right)}\\0\\\frac{d^{2}}{d t^{2}} y{\left(t \right)}\\K \frac{d}{d t} x{\left(t \right)} + M l \frac{d^{2}}{d t^{2}} \theta{\left(t \right)} + \left(M + m\right) \frac{d^{2}}{d t^{2}} x{\left(t \right)} - \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right) x{\left(t \right)}\\\lambda_{1} + \left(M + m\right) \frac{d^{2}}{d t^{2}} y{\left(t \right)}\\M g l \theta{\left(t \right)} + M l^{2} \frac{d^{2}}{d t^{2}} \theta{\left(t \right)} + M l \frac{d^{2}}{d t^{2}} x{\left(t \right)}\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}0 & 0 & 1 & 0\\0 & 0 & 0 & 1\\\frac{\frac{M^{2} l^{2} \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right)}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} + \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right)}{M + m} & \frac{M^{2} g l^{2}}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} & \frac{- \frac{K M^{2} l^{2}}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} - K}{M + m} & 0\\- \frac{M l \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right)}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} & - \frac{M g l}{- \frac{M^{2} l^{2}}{M + m} + M l^{2}} & \frac{K M l}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} & 0\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}0\\0\\- \frac{M^{2} g l^{2} \theta{\left(t \right)}}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} + \frac{d^{2}}{d t^{2}} x{\left(t \right)} - \frac{\left(- \frac{K M^{2} l^{2}}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} - K\right) \frac{d}{d t} x{\left(t \right)}}{M + m} - \frac{\left(\frac{M^{2} l^{2} \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right)}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} + \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right)\right) x{\left(t \right)}}{M + m}\\- \frac{K M l \frac{d}{d t} x{\left(t \right)}}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} + \frac{M g l \theta{\left(t \right)}}{- \frac{M^{2} l^{2}}{M + m} + M l^{2}} + \frac{M l \left(- M g - g m\right) \left(- a_{0} \omega^{2} + 2\right) x{\left(t \right)}}{\left(M + m\right) \left(- \frac{M^{2} l^{2}}{M + m} + M l^{2}\right)} + \frac{d^{2}}{d t^{2}} \theta{\left(t \right)}\end{matrix}\right]\)
array([[ 0. , 0. , 1. , 0. ],
[ 0. , 0. , 0. , 1. ],
[118.02314815, 24.25925926, -0.74074074, 0. ],
[-42.00112034, -12.19190721, 0.2636088 , 0. ]])
(array([-1.08479916e+01+0.j , 1.01090216e+01+0.j ,
-8.85400092e-04+1.95704657j, -8.85400092e-04-1.95704657j]),
array([[ 8.67633393e-02+0.j , 9.30902155e-02+0.j ,
-1.01408097e-03+0.08883113j, -1.01408097e-03-0.08883113j],
[-2.99703036e-02+0.j , -3.20133654e-02+0.j ,
-2.01894326e-04-0.44625769j, -2.01894326e-04+0.44625769j],
[-9.41207973e-01+0.j , 9.41051003e-01+0.j ,
-1.73845769e-01-0.00206325j, -1.73845769e-01+0.00206325j],
[ 3.25117601e-01+0.j , -3.23623804e-01+0.j ,
8.73347255e-01+0.j , 8.73347255e-01-0.j ]]))
5.2.2.3. changement de variables Y#
\(\displaystyle \left[\begin{matrix}1 & 0 & 0 & 0 & 0 & 0 & 0\\0 & 1 & 0 & 0 & 0 & 0 & 0\\0 & 0 & 1 & 0 & 0 & 0 & 0\\0 & 0 & 0 & M + m & 0 & M l \cos{\left(Y_{2, 0} \right)} & 0\\0 & 0 & 0 & 0 & M + m & M l \sin{\left(Y_{2, 0} \right)} & 0\\0 & 0 & 0 & M l \cos{\left(Y_{2, 0} \right)} & M l \sin{\left(Y_{2, 0} \right)} & M l^{2} \sin^{2}{\left(Y_{2, 0} \right)} + M l^{2} \cos^{2}{\left(Y_{2, 0} \right)} & 0\\0 & 0 & 0 & a_{0} \omega \sin{\left(\omega Y_{0, 0} \right)} - 2 Y_{0, 0} & 1 & 0 & 0\end{matrix}\right]\)
\(\displaystyle \left[\begin{matrix}Y_{3, 0}\\Y_{4, 0}\\Y_{5, 0}\\- K Y_{3, 0} + M l \sin{\left(Y_{2, 0} \right)} Y_{5, 0}^{2} - \left(- a_{0} \omega \sin{\left(\omega Y_{0, 0} \right)} + 2 Y_{0, 0}\right) Y_{6, 0}\\- K Y_{4, 0} - M g - M l \cos{\left(Y_{2, 0} \right)} Y_{5, 0}^{2} - g m + Y_{6, 0}\\- M g l \sin{\left(Y_{2, 0} \right)}\\- a_{0} \omega^{2} \cos{\left(\omega Y_{0, 0} \right)} Y_{3, 0}^{2} - \beta \left(- a_{0} \cos{\left(\omega Y_{0, 0} \right)} - Y_{0, 0}^{2} + Y_{1, 0}\right) + 2 Y_{3, 0}^{2}\end{matrix}\right]\)
5.2.3. Programmation#
5.2.3.1. parametres#
les valeurs de m,l,M et a0 sont fixés au début.
on choisira la valeur des parametres de penalisation \(\beta_1\) \(\beta_2\)
on prendra \(K=2.0\) , \(\omega=3.3\), \(g=10.0\)
le seul paramêtre variable est donc la position initiale \(x_0\)
Définir la valeurs de ces parametres et ecrire une fonction résidu qui calcul le résidu du système:
5.2.3.2. Vérification#
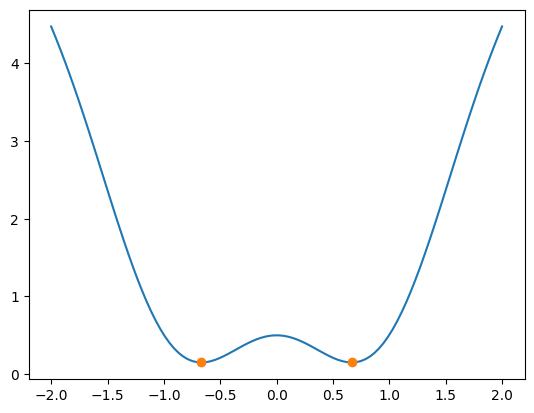
vérifier que pour les 2 positions d’équilibres le résidu est bien nul. On tracera aussi la courbe f(x) et la position des 2 points d’équilibre stables.
racine 0.666798402972126 err=5.773159728050814e-15
pour xe=0.666798402972126 res=[0.00000000e+00 0.00000000e+00 0.00000000e+00 5.34017275e-13
0.00000000e+00 0.00000000e+00 0.00000000e+00]
pour xe=-0.666798402972126 res=[ 0.00000000e+00 0.00000000e+00 0.00000000e+00 -5.34017275e-13
0.00000000e+00 0.00000000e+00 0.00000000e+00]
[<matplotlib.lines.Line2D at 0x7f00c0fe7880>]
5.2.4. Résolution#
ecrire une fonction solution qui calcule la solution en fonction d’une position initiale x0
5.2.4.1. Vérification#
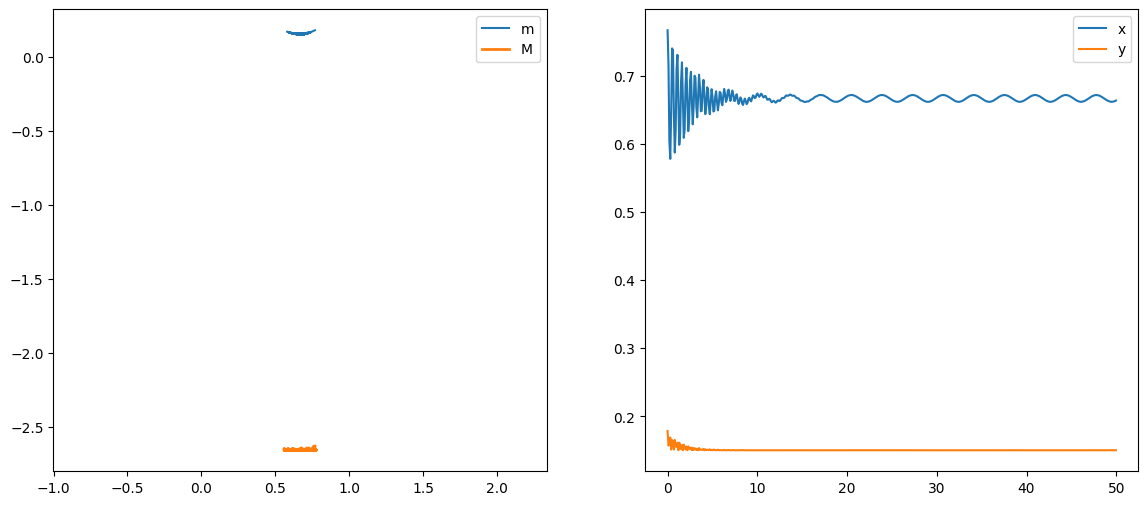
en choissisant une valeur de x0 proche de la position d’équilibre, vérifier que le mouvement du pendule est celui attendu.
CI Y0= [0.7667984 0.17848772 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 8156
<matplotlib.legend.Legend at 0x7f00bf6bffd0>
5.2.5. Analyse pour x0 grand#
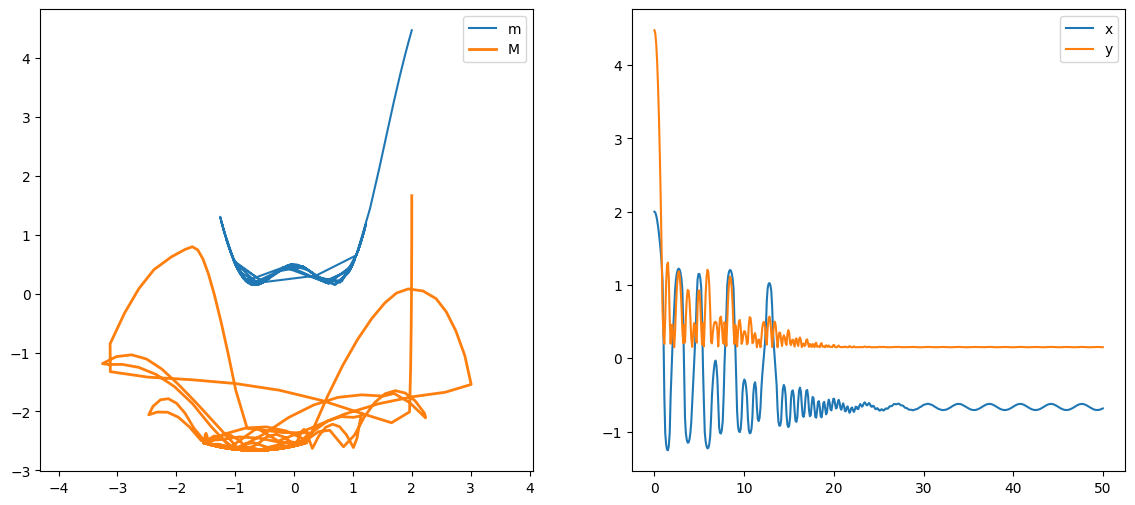
pour une valeur de x0 assez grande vérifier que le pendule peut passer d’une position déquilibre à l’autre.
CI Y0= [2. 4.4751163 0. 0. 0. 0. 0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 48738
<matplotlib.legend.Legend at 0x7f00bf17c130>
5.2.6. Etude en fonction de x0#
en faisant varier x0 de 0 2.0, déterminer la position finale en fonction de x0
CI Y0= [0.01 0.49982777 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 19210
CI Y0= [0.1095 0.47970045 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 18640
CI Y0= [0.209 0.42939947 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 18255
CI Y0= [0.3085 0.35768553 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 16019
CI Y0= [0.408 0.27772293 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 14544
CI Y0= [0.5075 0.20567298 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 10538
CI Y0= [0.607 0.15896717 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 5742
CI Y0= [0.7065 0.1544447 0. 0. 0. 0. 0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 4511
CI Y0= [0.806 0.20655316 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 11086
CI Y0= [0.9055 0.32580487 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 16031
CI Y0= [1.005 0.51765367 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 18990
CI Y0= [1.1045 0.78191212 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 20432
CI Y0= [1.204 1.11277161 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 25320
CI Y0= [1.3035 1.49942293 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 32708
CI Y0= [1.403 1.92721127 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 26079
CI Y0= [1.5025 2.37920202 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 31995
CI Y0= [1.602 2.83799026 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 35436
CI Y0= [1.7015 3.2875604 0. 0. 0. 0. 0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 37012
CI Y0= [1.801 3.71499745 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 39771
CI Y0= [1.9005 4.11186698 0. 0. 0. 0.
0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 44507
CI Y0= [2. 4.4751163 0. 0. 0. 0. 0. ]
dY0= [ 0. 0. 0. 0. -10. 0. 0.]
res= [ 0. 0. 0. 0. 0. 0. -10.]
Successful function return.
Nbre d'appel a rhs: 48738
Tracer la position finale en fonction de x0
Text(0.5, 1.0, 'position finale')
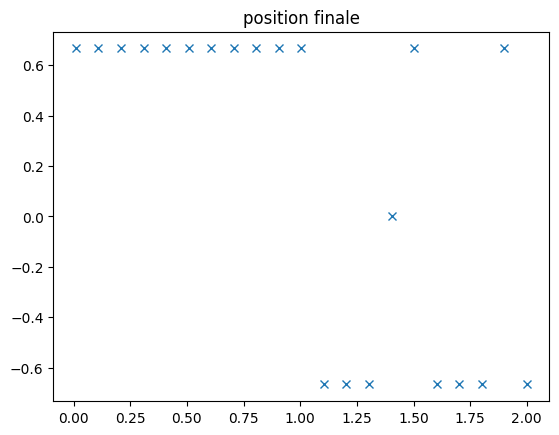
5.2.7. Conclusion#
écrire vos commentaires et conclusion
