4. Modélisation de la charge d’une grue#
Marc BUFFAT dp Mécanique, Université Lyon 1

%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
plt.rc('font', family='serif', size='14')
from IPython.display import display, Markdown, clear_output
def printmd(string):
display(Markdown(string))
from metakernel import register_ipython_magics
register_ipython_magics()
from sympy.physics.vector import init_vprinting
init_vprinting()
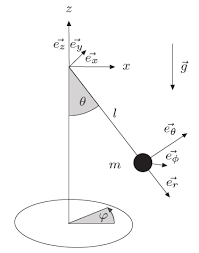
4.1. Modélisation de la charge: pendule sphérique (3D)#
pendule de masse m de longueur l
Réferentiel RO en O (z axe vertical)
2 ddl :
angle \(\phi_z\) (\(\phi\)) rotation autour de Oz
angle \(\phi_y\) (\(\pi/2 - \theta\)) rotation autour de Oy
parametres
m, g, l
\(\omega = \sqrt{\frac{g}{l}}\)
from sympy.physics.mechanics import dynamicsymbols, Point, ReferenceFrame
from sympy.physics.mechanics import Particle, RigidBody, Lagrangian, LagrangesMethod
# definition ddl et parametres
phiy, phiz = dynamicsymbols('phi_y phi_z')
phiyp, phizp = dynamicsymbols('phi_y phi_z',level=1)
t = sp.Symbol('t')
m , l , omega = sp.symbols('m l omega')
g = omega**2*l
4.2. Repéres, Point et position#
# repêre
O = Point('O')
RO = ReferenceFrame('R_O')
R1 = ReferenceFrame('R_1')
R1.orient(RO,'Axis',[phiz,RO.z])
R2 = ReferenceFrame('R_2')
R2.orient(R1,'Axis',[phiy,R1.y])
M = Point('M')
M.set_pos(O,-l*R2.z)
display("OM=",M.pos_from(O).express(RO))
'OM='
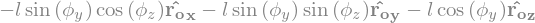
4.3. Cinématique#
calcul directe: $\( \vec{V_M} = \frac{d \vec{OM}}{dt}\)$
composition des mouvement
# calcul directe
from sympy.physics.vector import express,time_derivative
display("OM=",express(M.pos_from(O),RO))
display("VM=",express(time_derivative(M.pos_from(O),RO),R2).simplify())
'OM='
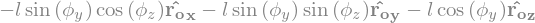
'VM='

# utilisation de la composition des mouvement
O.set_vel(RO,0.)
M.set_vel(R2,0.)
### BEGIN SOLUTION
M.v2pt_theory(O,RO,R2)
### END SOLUTION
# definition de la masse ponctuelle
Masse = Particle('Masse',M,m)
display("Qte mouvement:",Masse.linear_momentum(RO))
'Qte mouvement:'
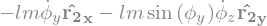
4.4. Formulation de Lagrange#
# calcul lagrangien adminensionne par m l**2
display("Ec=",Masse.kinetic_energy(RO).simplify())
La = 0
### BEGIN SOLUTION
Masse.potential_energy = m*g*M.pos_from(O).dot(RO.z)
display("U=",Masse.potential_energy)
# calcul lagrangien (adimensionalisé)
La = Lagrangian(RO,Masse)/(l**2*m)
La = La.simplify()
### END SOLUTION
display("La=",La)
'Ec='
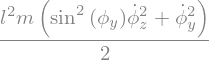
'U='
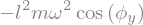
'La='
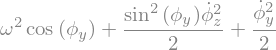
4.5. Equations de Lagrange#
propriétés de conservation
mt cinétique
énergie (système conservatif)
LM = LagrangesMethod(La,[phiy,phiz],frame=RO)
Eq = LM.form_lagranges_equations()
display("Equation de Lagranges:",Eq)
'Equation de Lagranges:'
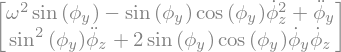
# montrez que la dernière equation implique que le moment angulaire pz suivant z est constant
pz = sp.symbols('p_z')
### BEGIN SOLUTION
Eqpz = sp.sin(phiy)**2*phizp
display("Cons. pz:",sp.Eq(Eqpz,pz))
display("vérification dérivée:",Eqpz.diff(t))
print("Eq[1]:")
display(Eq[1])
### END SOLUTION
'Cons. pz:'
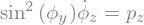
'vérification dérivée:'

Eq[1]:

# montrez que l'on a conservation energie totale
Et = 0
### BEGIN SOLUTION
Et = ((Masse.kinetic_energy(RO) + Masse.potential_energy)/(l**2*m)).simplify()
display("Et=",Et)
display("dérivée:",Et.diff(t).simplify())
print("Eq[0]*phiyp + Eq[1]*phizp")
(Eq[0]*phiyp+Eq[1]*phizp).simplify()
### END SOLUTION
'Et='
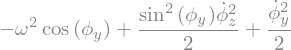
'dérivée:'
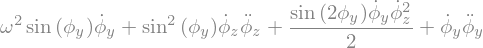
Eq[0]*phiyp + Eq[1]*phizp
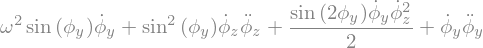
4.6. Mise sous forme EDP ordre 1#
\[ \dot{Y} = F(Y,t)\]
Le formalisme de Lagrange fournit le système
\[ A \dot{Y} = B(Y,t)\]
d’où $\( F(Y,t) = A^{-1} B(Y,t) \)$
A=LM.mass_matrix_full
B=LM.forcing_full
display("A=",A,"B=",B)
# calcul de F
FY = 0
### BEGIN SOLUTION
FY = A.inv()*B
### END SOLUTION
display("F(Y,t):",FY)
'A='

'B='
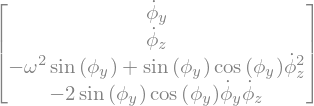
'F(Y,t):'
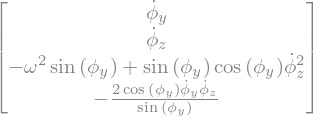
4.7. Paramêtres pour la résolution numérique#
# conversion fonction BY
smFY = sp.lambdify([phiy,phiz,phiyp,phizp,omega],FY,'numpy')
# fonction F(Y)
def F(Y,t):
'''2nd membre de l EDO dY/dt = F(Y,t) avec Y=[phiy,phiz,phiyp,phizp]'''
global Omega
### BEGIN SOLUTION
FF =smFY(Y[0],Y[1],Y[2],Y[3],Omega)
return FF[:,0]
### END SOLUTION
# parametres
LL = 2.0
Omega = np.sqrt(10.0/LL)
valnum = [(l,LL),(omega,Omega)]
print("T={:.3f} omega={:.3f}".format(2*np.pi/Omega,Omega))
T=2.810 omega=2.236
4.8. Mouvement de précession (rotation autour de Oz)#
\(\phi_y= cste\) implique \(\dot{\phi_z} = k_z = cste\)
\[ \phi_z (t) = k_z t \]
# mouvement avec phiy=cste => phiz = kz*t
display(sp.Eq(Eq[1].subs({phiy.diff(t) : 0}),0))
# d'où la solution phi_y
from sympy.solvers import solve
kz = sp.Symbol('k_z')
Eq0 = Eq[0].subs({phiy.diff(t,t) : 0, phiz.diff(t) : kz})/ sp.sin(phiy)
Eq0 = Eq0.simplify()
display("Equation sur phiy",Eq0)
display(sp.Eq(phiy,solve(Eq0,phiy)[0]))
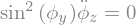
'Equation sur phiy'
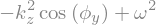

4.8.1. solution numérique#
# solution exacte
Kz = 1.2*Omega
Phiy0 = -np.arccos(Omega**2/Kz**2)
print("Phiy={:.2f} dPhyz={:.2f}".format(Phiy0,Kz))
Phiy=-0.80 dPhyz=2.68
# simulation
from scipy.integrate import odeint
# mouvement precession
T = 8.0
N = 200
tt = np.linspace(0,T,N)
### BEGIN SOLUTION
Y0 = np.array([Phiy0,0.0,0.0,Kz])
sol = odeint(F,Y0,tt,atol=1.e-12,rtol=1.e-12)
PHIY = sol[:,0]
PHIZ = np.mod(sol[:,1],2*np.pi)
DPHIY= sol[:,2]
DPHIZ= sol[:,3]
### END SOLUTION
# trace de la solution
plt.figure(figsize=(12,8))
plt.subplot(2,1,1)
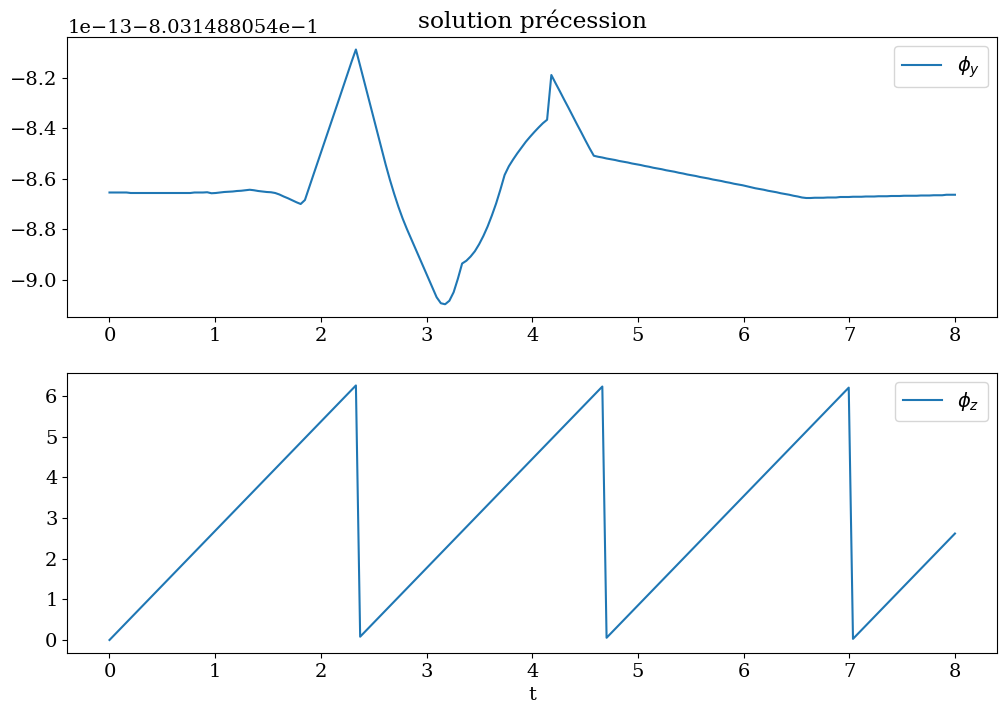
plt.title("solution précession");
plt.plot(tt,PHIY,label="$\phi_y$")
plt.legend()
plt.subplot(2,1,2)
plt.plot(tt,PHIZ,label="$\phi_z$")
plt.legend()
plt.xlabel('t');
# visualisation de la trajectoire: calcul position de P dans RO
from validation.Pendule3D import Trajectoire3D
Mx = sp.lambdify([phiy,phiz],M.pos_from(O).dot(RO.x).subs(valnum),'numpy')
My = sp.lambdify([phiy,phiz],M.pos_from(O).dot(RO.y).subs(valnum),'numpy')
Mz = sp.lambdify([phiy,phiz],M.pos_from(O).dot(RO.z).subs(valnum),'numpy')
Trajectoire3D(Mx(PHIY,PHIZ),My(PHIY,PHIZ),Mz(PHIY,PHIZ),LL)
4.9. Mouvement général#
perturbation de la solution précédente
T = 16.0
N = 200
tt = np.linspace(0,T,N)
# cas mouvement perturbee
Y0 = np.array([Phiy0-0.2,0.0,0.,Kz-0.2])
# cas quelconque
#Y0 = np.array([-0.2,0.0,2.,8.])
sol = odeint(F,Y0,tt,atol=1.e-12,rtol=1.e-12)
PHIY = sol[:,0]
PHIZ = np.mod(sol[:,1],2*np.pi)
DPHIY= sol[:,2]
DPHIZ= sol[:,3]
# trace de la solution
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
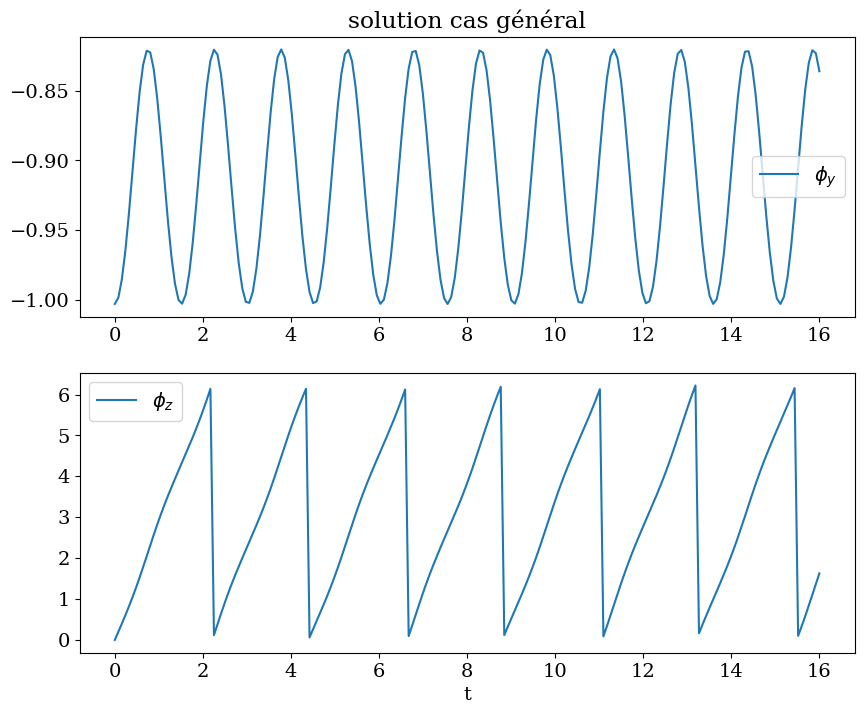
plt.title("solution cas général");
plt.plot(tt,PHIY,label="$\phi_y$")
plt.legend()
plt.subplot(2,1,2)
plt.plot(tt,PHIZ,label="$\phi_z$")
plt.legend()
plt.xlabel('t');
# visualisation 3D de la trajectoire
Trajectoire3D(Mx(PHIY,PHIZ),My(PHIY,PHIZ),Mz(PHIY,PHIZ),LL)
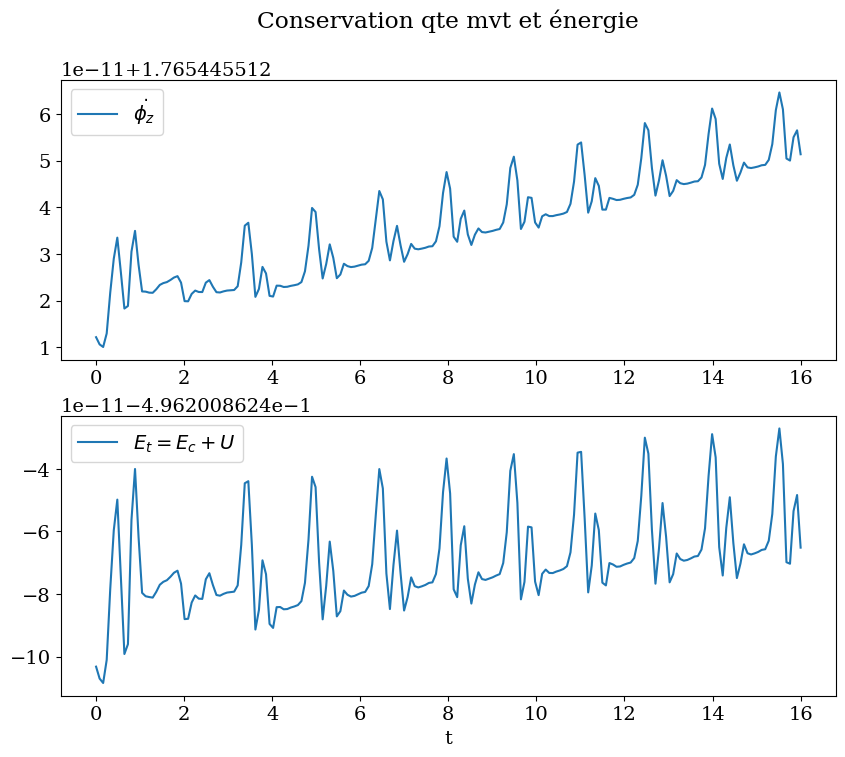
# verification conservation mt cinetique et energie
PZ = np.sin(PHIY)**2*DPHIZ
ET = sp.lambdify([phiy,phiz,phiyp,phizp],Et.subs(valnum),'numpy')
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.plot(tt,PZ,label="$\dot{\phi_z}$")
plt.legend()
plt.title("Conservation qte mvt et énergie\n")
plt.subplot(2,1,2)
plt.plot(tt,ET(PHIY,PHIZ,DPHIY,DPHIZ),label="$E_t = E_c + U$")
plt.legend()
plt.xlabel('t');
4.10. Cas d’un cable anti-rotation#
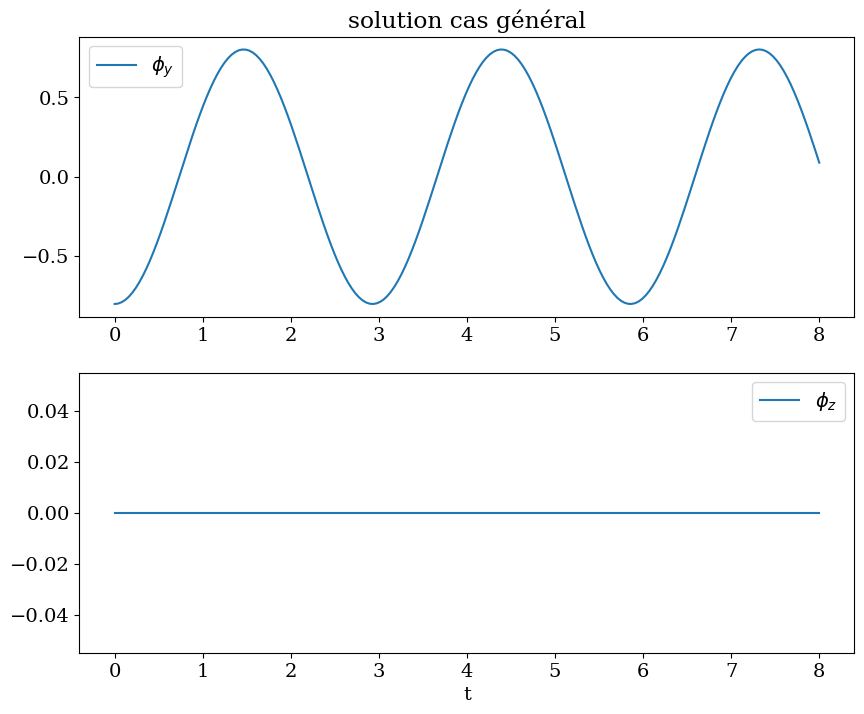
les grues ont en général un filin tressé qui limite la rotation autour de Oz $\(\dot{\phi_z} = 0 \)$
On a donc plus qu’une oscillation suivant Oy
T = 8.0
N = 200
tt = np.linspace(0,T,N)
# cas sans rotation autour de Oz
Y0 = np.array([Phiy0,0.0,0.0,0.])
sol = odeint(F,Y0,tt,atol=1.e-12,rtol=1.e-12)
PHIY = sol[:,0]
PHIZ = sol[:,1]
DPHIY= sol[:,2]
DPHIZ= sol[:,3]
plt.figure(figsize=(10,8))
plt.subplot(2,1,1)
plt.title("solution cas général");
plt.plot(tt,PHIY,label="$\phi_y$")
plt.legend()
plt.subplot(2,1,2)
plt.plot(tt,PHIZ,label="$\phi_z$")
plt.legend()
plt.xlabel('t');
# visualisation 3D de la trajectoire
Trajectoire3D(Mx(PHIY,PHIZ),My(PHIY,PHIZ),Mz(PHIY,PHIZ),LL)
