10.2. TP méthode de minimisation multi-dimensionnelle#
Marc Buffat Dpt mécanique, UCB Lyon 1
%matplotlib inline
#algèbre linéaire
import numpy as np
import sympy as sp
import time
#représentation des résultats
import matplotlib.pyplot as plt
from IPython.display import display,Markdown
def printmd(text):
display(Markdown(text))
plt.rc('font', family='serif', size='18')
from validation.validation import info_etudiant
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
NOM,PRENOM,NUMERO_ETUDIANT=info_etudiant()
#raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Login étudiant {} {} uid={}**".format(NOM,PRENOM,_uid_))
# fonctionnelle a minimiser
import pwd,sys
libpath=pwd.getpwnam('cours')[5]+'/IntroIA/lib'
sys.path.insert(0, libpath)
from Fonctionnelle import Fonctionnelle
J = Fonctionnelle(_uid_)
printmd("**Fonctionnelle J à minimiser**")
J.info()
ERREUR: numéro d’étudiant non spécifié!!!
Login étudiant Marc BUFFAT uid=137764122
Fonctionnelle J à minimiser
Fonctionnelle J(X)
dimension de X : 43
minimum de J : -1.7692176662626187
pour ||X|| < 1.0
10.2.1. Objectifs#
Trouver le vecteur X minimisant la fonction J(X).
Cette fonction J() est implémentée en Python comme un objet (instance de classe):
J : nom de l’objet
J.dim() : dimension de X, i.e. le nombre de variables dont J dépend
J(X) : calcul la valeur de J pour un vecteur X de dimension J.dim()
J.grad(X) : calcul le gradient de J en X
J.err(X) : calcul la norme de l’erreur ||X-Xe|| où Xe minimise J(X)
J.min() : calcul le minimum de J
10.2.2. Minimisation 1D#
Etude de la minimisation de \(J(\mathbf{X})\) dans une direction \(\mathbf{D}\) fixée
On choisit un vecteur \(D\) (imposé), et on cherche à minimiser \(J(\alpha \mathbf{D})\)
Dans les cellules suivantes:
calculer \(J(\alpha \mathbf{D})\) pour des valeurs de \(\alpha\) entre -2 et 2
tracer la fonction \(J(\alpha)\)
10.2.2.1. Minimisation 1D#
Principe de la méthode de dichotomie pour la minimisation
On considère une fonction continue \(f(x)\) sur un intervalle \([a,b]\). On suppose que \(f(x)\) admet un minimum unique sur cet intervalle.
À chaque itération :
On choisit deux points proches du milieu :
\(x_1=m−\delta\) , \(x_2=m+\delta\) , avec \(m=(a+b)/2\)
On compare \(f(x_1)\) et \(f(x_2)\)
Si \(f(x_1) < f(x_2)\) le minimum est à gauche \(\leadsto\) \(b=x_2\)
sinon, le minimum est à droite \(\leadsto\) \(a=x_1\)
On répète jusqu’à ce que \(∣b−a∣\) soit petit (tolérance).
Ecrire la fonction python
MinDichotomie(f, a, b, tol=1e-5, delta=1e-6, max_iter=1000)
qui minimise par dichotomie la fonction 1D \(f(x)\)
Appliquer la fonction avec les paramètres précédents pour calculer la minimisation de \(J(X)\) dans la direction \(D\) précédente.
Comparer pour vérifier avec la solution scipy calculer dans la section suivante.
# application
### BEGIN SOLUTION
F = lambda alpha:J(alpha*D)
amin, fmin, nit = MinDichotomie(F,-1,1)
print(f"Minimum Jmin={fmin} alpha={amin} it={nit}")
### END SOLUTION
---------------------------------------------------------------------------
NameError Traceback (most recent call last)
Cell In[3], line 5
1 # application
2
3 ### BEGIN SOLUTION
4 F = lambda alpha:J(alpha*D)
----> 5 amin, fmin, nit = MinDichotomie(F,-1,1)
6 print(f"Minimum Jmin={fmin} alpha={amin} it={nit}")
NameError: name 'MinDichotomie' is not defined
10.2.2.2. Utilisation bibliothèque scipy#
utiliser la fonction
minimize_scalarde scipy pour calculer le mimimum en \(\alpha\)mettre le resultat dans la variable
alpha_min
10.2.3. Minimisation Multi-dimensionnel#
10.2.3.1. Minimisation de type line-search#
méthode sans calcul de gradient
On choisit arbitrairement des directions de descente \(\vec{d}\)
pour chaque direction, on minimise en 1D dans cette direction
Par exemple , si \(F(x_1,x_2,..x_n)\) , on choisit alternativement la direction de chaque paramétre \(x_k\):
\(\vec{d}= [\delta_{ik}]\)
Application:
appliquer la méthode précédente pour minimiser \(J(X)\) à partir de \(X=0\)
on utilisera successivement les directions des n paramétres X: i.e. D=\([\delta_{ik}]\)
afficher la solution \(X\) et l’erreur avec \(J.err(X)\)
# minimisation multi-dim
### BEGIN SOLUTION
### END SOLUTION
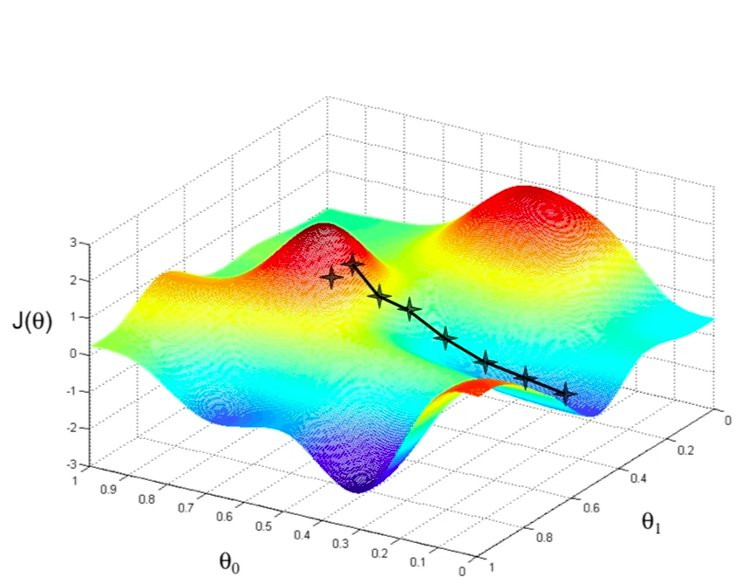
10.2.3.2. Minimisation de type gradient#
On choisit comme direction de descente la direction opposée au gradient:
\(\vec{d} = -\vec{\nabla} F(X)\)
Application:
appliquer la méthode de gradient pour minimiser \(J(X)\) à partir de \(X=0\)
on utilisera n (dimension de X) itérations de gradients
afficher la solution \(X\) et l’erreur avec \(J.err(X)\) et comparer avec la méthode précédente
# methode de gradient
### BEGIN SOLUTION
### END SOLUTION
10.2.4. Minimisation multi-dimensionelle avec scipy#
utilisation de la bibliothéque scipy
fonction minimize (minimisation locale)
méthode de gradients exactes: Gradients Conjugués, Newton GC,
méthode de gradients approchées: BFGS,
line search Powell, Simplex Nelder-Mead
optimisation globale
simulated annealing
Dans la cellule suivante, définir 2 nouvelles fonctions
F(X) qui calcul J(X)
Fgrad(X) qui calcule le gradient
on définit des fonctions python car les méthodes de minimisation n’autorisent pas les méthodes de classe
F = None
Fgrad = None
### BEGIN SOLUTION
### END SOLUTION
X0 = np.zeros(J.dim())
10.2.4.1. Méthode par défaut#
pour chacune des méthodes:
on calcule la solution obtenue Xe,
la valeur de J
l’erreur (qui doit etre inférieure à 1.e-5)
Il faut aussi jouer sur les paramètres optionnels de la fonction
from scipy.optimize import minimize
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.4.2. Méthode de gradient conjugué#
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.4.3. Méthode de gradient conjugué avec Newton#
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.4.4. Méthode BFGS (gradient avec calcul d’un gradient stocastique)#
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.4.5. Algorithme Powell (line search 2D)#
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.4.6. Simulated annealing#
from scipy.optimize import dual_annealing
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.4.7. Méthode du Simplex (Nelder-Mead)#
Xe = None
### BEGIN SOLUTION
### END SOLUTION
10.2.5. Analyse#
comparaison des méthodes
coût
précision
