6. Différentiation Automatique#
(C) Marc BUFFAT, dpt Mécanique, Université Claude Bernard Lyon 1
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
6.1. Problème de minimisation en machine learning#
En machine learning, l’objectif est de trouver une loi \(U(X,\beta)\) donnant la valeur de \(U\) en fonction des données \(X\), loi qui dépend des paramètres \(\beta\).
Les paramètres \(\beta\) sont optimisés de façon à minimiser une fonction coût \(J(U)\) à partir d’une base de données où on connait la valeur de \(U\) pour des valeurs de \(X\) (apprentissage supervisé).
Pour minimiser \(J(U)\) on utilise une méthode de gradient, qui consiste à calculer la nouvelle valeur des paramètres \(\beta_{k+1}\): en se déplaçant dans la direction opposée au gradient de \(J(U)\):
où
\(\beta_k\) représente les valeurs des paramètres connus du modèle à l’étape k
\(\beta_{k+1}\) les nouvelles valeurs des paramètres
\(\alpha\) est le taux de descente (learning rate)
\(\nabla_{\beta} L\) est le gradient de la fonction coût par rapport aux paramètres
Dans cette méthode de descente, le calcul de ce gradient est la phase la plus complexe et la plus couteuse, en particulier lorsque le nombre de paramètres est très important.
6.1.1. Méthode de calcul du gradient#
Pour calculer le gradient de d’une fonction \(J(U)\), il existe plusieurs méthodes :
la dérivation symbolique :
on calcule la dérivée analytique (à l’aide d’un outil de calcul formel), mais cela suppose une connaissance explicite de \(J(U(\beta))\)
la dérivation numérique :
on calcule une approximation numérique par différences finies. C’est en principe le plus simple, mais peut être très coûteux et peu précis
la différentiation automatique :
on utilise le code informatique de définition de \(J(U)\), qui est sous la forme d’un graphe et la règle dé dérivation composée pour générer un code informatique qui calcule la valeur du gradient
6.1.2. Exemple simple#
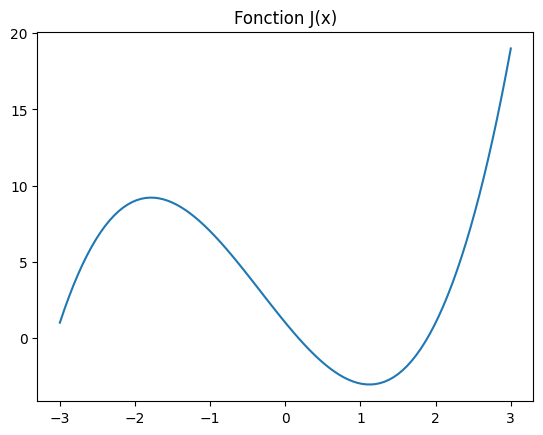
Pour présenter ces différentes méthodes, nous allons considérer la minimisation de la fonction \(J(x)\) sur l’intervalle \([-3,3]\) suivante:
En traçant la fonction sur \([-3,3]\), on vérifie qu’elle admet bien un minimum local près de 1.
Nous allons ensuite examiner différentes façon de calculer la valeur de sa dérivée \(dJ(x)\)
X = np.linspace(-3,3,101)
J = lambda x: x**3 + x**2 - 6*x + 1
JX = J(X)
plt.plot(X,JX)
plt.title("Fonction J(x)");
6.2. Dérivation symbolique#
Sous Python, on va utiliser la bibliothèque sympy et la fonction Derivativepour calculer analytiquement le gradient
et la méthode doit() pour faire le calcul immédiatement.
En utilisant la fonction display (au lieu de print), on a un affichage mathématique du résultat.
Pour pouvoir l’utiliser, on va ensuite convertir la fonction symbolique en fonction numpy avec
import sympy as sp
x = sp.symbols('x')
expr = x**3 + x**2 - 6*x + 1
display(expr)
DJ = sp.Derivative(expr,x).doit()
display(DJ)
dJ = sp.lambdify(x,DJ,"numpy")
plt.plot(X,dJ(X))
plt.hlines(0,-3,3)
<matplotlib.collections.LineCollection at 0x7f3729dcbbb0>
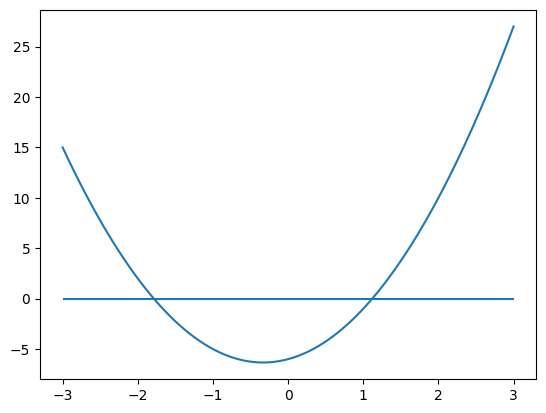
6.2.1. Minimisation de J#
en utilisant la méthode de descente par gradient (dans ce cas méthode de Newton), on calcule la suite itérative \(x_k\) $\(x_{k+1} = x_k - \alpha*\nabla J(x_k) \)\( En partant d'une valeur initiale \)x=3\( et en fixant un pas de descente \)\alpha=0.1\(, on obtiens la position du minimum avec une précision machine de \)10^{-16}$
x = 3
alpha = 0.1
N = 20
for i in range(N):
x = x - alpha*dJ(x)
print(x,J(x),dJ(x))
print("Position du minimum x=",x)
0.2999999999999998 -0.6829999999999992 -5.130000000000001
0.813 -2.6796632030000005 -2.3910930000000006
1.0521093000000001 -3.041106286907482 -0.5749794625605293
1.1096072462560531 -3.060235458645886 -0.08710078465606941
1.11831732472166 -3.060665044438249 -0.011464434238847687
1.1194637681455448 -3.0606724624016604 -0.0014750791370445882
1.1196112760592494 -3.060672585151872 -0.00018921944443839323
1.1196301980036931 -3.060672587171627 -2.4263147246017525e-05
1.1196326243184178 -3.060672587204838 -3.1110487217489435e-06
1.11963293542329 -3.0606725872053833 -3.9889970260276186e-07
1.1196329753132601 -3.060672587205392 -5.114700929453875e-08
1.119632980427961 -3.060672587205392 -6.558081189211862e-09
1.119632981083769 -3.060672587205392 -8.408793661374148e-10
1.119632981167857 -3.060672587205392 -1.078177547242376e-10
1.1196329811786387 -3.060672587205392 -1.3823608924212749e-11
1.1196329811800212 -3.060672587205393 -1.77280412572145e-12
1.1196329811801984 -3.060672587205392 -2.2737367544323206e-13
1.119632981180221 -3.060672587205393 -3.019806626980426e-14
1.1196329811802241 -3.060672587205392 -3.552713678800501e-15
1.1196329811802246 -3.060672587205393 8.881784197001252e-16
Position du minimum x= 1.1196329811802246
6.3. Dérivation numérique#
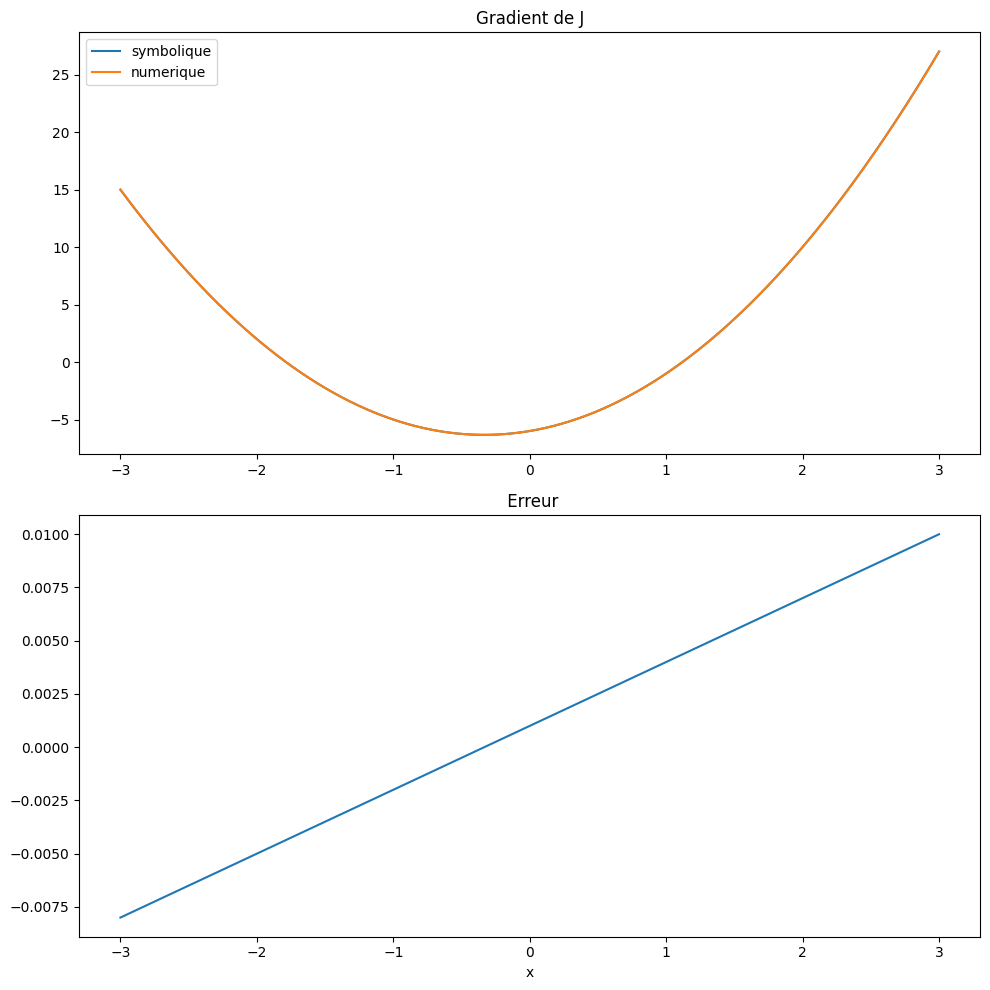
Au lieu de calculer la dérivée exacte, qui nécessite la connaissance de l’expression analytique de J, on peut utiliser une dérivation numérique, en utilisant un d’enveloppement de Taylor à l’ordre 1:
pour obtenir une valeur numérique du gradient en fonction de valeur numérique de J en se fixant un petit accroissement dx de x
def dJn(x):
dx = 0.001
return (J(x+dx)-J(x))/dx
# tracer
fig = plt.figure(figsize=(10,10))
plt.subplot(2,1,1)
plt.plot(X,dJn(X),label="symbolique")
plt.plot(X,dJ(X),label="numerique")
plt.legend()
plt.title("Gradient de J")
plt.subplot(2,1,2)
plt.title(" Erreur")
plt.plot(X,dJn(X)-dJ(X))
plt.xlabel("x")
plt.tight_layout()
On peut alors utiliser la méthode précédente pour calculer une approximation du minimum de J.
Avec dx=0.01, on constate que la précision du calcul est beaucoup plus faible (\(\approx 4.10^{-2}\)). Avec plus petit \(dx=0.001\) la précision est (\(\approx 4.10^{-3}\)).
La méthode numérique est donc d’ordre 1.
x = 3
alpha = 0.1
N = 20
for i in range(N):
x = x - alpha*dJn(x)
print(x,J(x),dJ(x),dJn(x))
print("Position du minimum x=",x)
1.119132952503274 -3.0606714974806746 -0.004358398857365664 0.0
Position du minimum x= 1.119132952503274
6.4. Différentiation automatique#
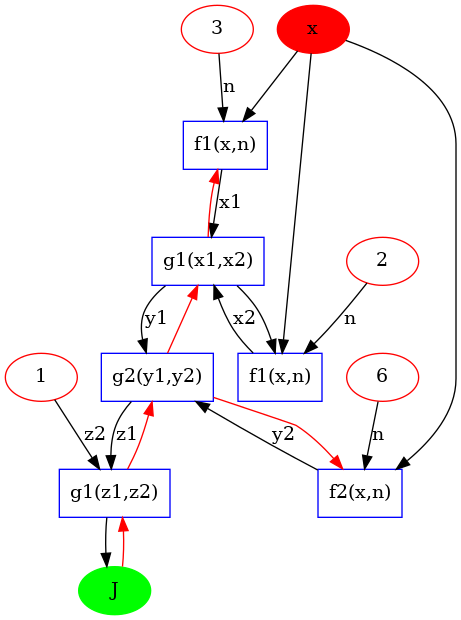
On représente l’expression sous la forme d’un graphe avec l’application de fonctions simples. Pour la fonction étudiée:
le graphe est donné sur la figure suivante avec les fonctions simples suivantes:
\(f1(x,n) = x^n\)
\(f2(x,n) = x*n\)
\(g1(x1,x2) = x1 + x2 \)
\(g2(x1,x2) = x1 - x2 \)
On peut donc écrire:
# generation du graph
if False :
import graphviz
gr = graphviz.Digraph(filename="graph.gb",format='png')
names = ["A1","A2","A3","A4","A5","B1","B2","B3","C1","C2","D1","E1"]
positions =["x","3","2","6","1","f1(x,n)","f1(x,n)","f2(x,n)","g1(x1,x2)","g2(y1,y2)","g1(z1,z2)","J"]
for name, position in zip(names, positions):
if name == "A1" :
gr.node(name, position,color="red",style="filled")
elif name[0]=="A" :
gr.node(name, position,color="red")
elif name == "E1" :
gr.node(name, position,color="green",style="filled")
else :
gr.node(name, position,color="blue",shape = "box")
# edges
gr.edge("A1","B1"); gr.edge("A2","B1",label="n");
gr.edge("A1","B2"); gr.edge("A3","B2",label="n")
gr.edge("A1","B3"); gr.edge("A4","B3",label="n")
gr.edge("B1","C1",label="x1"); gr.edge("B2","C1",label="x2");
gr.edge("C1","C2",label="y1"); gr.edge("B3","C2",label="y2");
gr.edge("C2","D1",label="z1"); gr.edge("A5","D1",label="z2")
gr.edge("D1","E1")
# display graph
#display(gr)
gr.render()
# second graphe
gr1 = gr.copy()
gr1.edge("E1","D1",color="red")
gr1.edge("D1","C2",color="red");
gr1.edge("C2","C1",color="red"); gr1.edge("C2","B3",color="red")
gr1.edge("C1","B1",color="red"); gr1.edge("C1","B2",coor="red");
#display(gr1)
gr1.render(filename="graph1.gb")
Graphe directe
Représentation du DAG: direct acyclic graph dont les noeuds sont des fonctions, les branches entrantes sont les données (tenseurs) et les branches sortantes les résultats (tenseurs).

Pour calculer le gradient de J , on utilise la dérivation composée:
ce qui donne
et ainsi de suite ..
On constate que, de façon naturel, le calcul du gradient commence par la dérivation de la dernière fonction du graph (g1), puis en remontant ensuite dans le graphe.
C’est l’ordre inverse de l’évaluation de la fonction \(J\) et on parle de calcul en mode inverse (reverse mode).
On parle alors de reverse mode automatic differentiation
Graphe inverse (reverse)
Parcourt du graph DAC de la racine (root) vers les feuilles (leaves) (avec les branches en rouge)
6.4.1. Reverse Mode Automatic Differentiation#
Un début d’implémentation de ce calcul du gradient en mode reverse mode est donné ci-dessous et utilise la notion de classde Python avec la possibilité de redéfinir les opérateurs de base.
Le principe est de définir les fonctions simples à partir des opérateurs de base, dont on connaît la dérivée :
pour \(f1(x,n) = x^n \), alors \(\frac{f1}{dx} = n x^{n-1}\)
pour \(f2(x,x) = n*x \) alors \(\frac{f2}{dx} = n \)
pour \(g1(x1,x2) = x1 + x2 \) alors \(\frac{g1}{dx} = \frac{dx1}{dx} + \frac{dx2}{dx}\)
pour \(g2(x1,x2) = x1 - x2 \) alors \(\frac{g1}{dx} = \frac{dx1}{dx} - \frac{dx2}{dx}\)
On définit pour cela la classe Node avec, pour chaque opérateur / fonction élémentaire, la définition du calcul de la dérivée dans une sous-fonction backward utiliser pour le calcul du gradient en reverse mode.
Remarques on calcule \(df = \frac{df}{dx} \, dx\), on spécifie donc \(dx=1\) pour calculer la dérivée
# classe de base pour décrire l'arbre de calcul de la fonction à minimiser
class Node:
def __init__(self, value, nom="Node"):
self.value = value
self.name = nom+"="+str(value)
self.grad = 0
self._backward = lambda: None
# this is defined as the forward mode is done based on the computation graph.
self._prev = set()
def __add__(self, other):
other = other if isinstance(other, Node) else Node(other)
out = Node(self.value + other.value," + ")
out._prev = {self, other}
def _backward():
self.grad += out.grad
other.grad += out.grad
out._backward = _backward
return out
def __sub__(self, other):
other = other if isinstance(other, Node) else Node(other)
out = Node(self.value - other.value," - ")
out._prev = {self, other}
def _backward():
self.grad += out.grad
other.grad -= out.grad
out._backward = _backward
return out
def __mul__(self, other):
other = other if isinstance(other, Node) else Node(other)
out = Node(self.value * other.value," * ")
out._prev = {self, other}
def _backward():
self.grad += other.value * out.grad
other.grad += self.value * out.grad
out._backward = _backward
return out
def __pow__(self, n):
out = Node(self.value ** n, " ** ")
out._prev = {self}
def _backward():
self.grad += n * (self.value ** (n-1)) * out.grad
out._backward = _backward
return out
def backward(node):
topo = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
build_topo(node)
# dx = 1
node.grad = 1
for node in reversed(topo):
node._backward()
# utilisation
x = Node(2.0,"x")
y = x**3 + x**2 - x*6 + 1
backward(y)
# evaluation
print(f"f(2) = {y.value}, f'(2) = {x.grad}")
print("valeurs exactes ",J(2),dJ(2))
f(2) = 1.0, f'(2) = 10.0
valeurs exactes 1 10
# evaluation du graphe
x = Node(2.0,"x")
y = x**3 + x**2 - x*6 + 1
topo = []
noms = []
visited = set()
def build_topo(v):
if v not in visited:
visited.add(v)
for child in v._prev:
build_topo(child)
topo.append(v)
noms.append(v.name)
build_topo(y)
# fonction
print("Evaluation f(x) pour x=2 (forward)")
print(noms)
print("F(2)=",noms[-1],y.value)
# gradient
print("Evaluation du gradient")
y.grad = 1
noms = []
grads= []
for node in reversed(topo):
noms.append(node.name)
grads.append(node.grad)
node._backward()
print(noms)
print(grads)
print("Valeur du gradient ",x.grad)
Evaluation f(x) pour x=2 (forward)
['Node=6', 'x=2.0', ' * =12.0', ' ** =4.0', ' ** =8.0', ' + =12.0', ' - =0.0', 'Node=1', ' + =1.0']
F(2)= + =1.0 1.0
Evaluation du gradient
[' + =1.0', 'Node=1', ' - =0.0', ' + =12.0', ' ** =8.0', ' ** =4.0', ' * =12.0', 'x=2.0', 'Node=6']
[1, 1, 1, 1, 1, 1, -1, 10.0, -2.0]
Valeur du gradient 10.0
# tracer de la dérivée
dY = np.zeros(X.size)
for i in range(X.size):
x = Node(X[i])
y = x**3 + x**2 - x*6 + 1
backward(y)
dY[i] = x.grad
#
plt.subplot(2,1,1)
plt.plot(X,dJn(X),label="symbolique")
plt.plot(X,dY,label="automatique")
plt.legend()
plt.title("Gradient de J")
plt.subplot(2,1,2)
plt.title(" Erreur")
plt.plot(X,dY-dJ(X))
plt.xlabel("x")
plt.tight_layout()
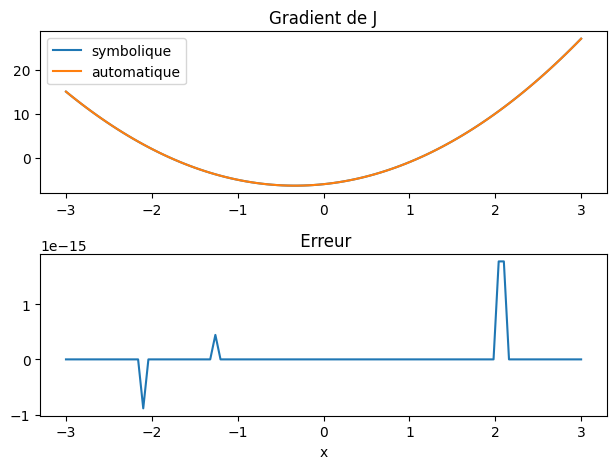
En utilisant la méthode descente par gradient avec les mêmes paramètres que précédemment, on on obtiens la position du minimum avec une précision machine de \(10^{-15}\), c.a.d. la même précision qu’avec le calcul symbolique.
xa = 3
alpha = 0.1
N = 20
for i in range(N):
x = Node(xa)
y = x**3 + x**2 - x*6 + 1
backward(y)
dJa = x.grad
xa = xa - alpha*dJa
print(xa,y.value,dJa)
print("Position du minimum x=",xa)
1.1196329811802246 -3.060672587205392 -3.552713678800501e-15
Position du minimum x= 1.1196329811802246
6.4.2. Bibliothèques Python#
ce calcul de différentiation automatique est fourni par des bibliothèques Python
Jax avec en particulier
jax.grad(f)PyTorch avec la différentiation automatique torch.autograd, qui est utilisée dans les versions optimisées des réseaux de neurones
6.5. Utilisation de pytorch autograd#
Pytorch est une bibliothèque Python permettant de manipuler efficacement des tenseurs et disponible en OpenSource.
Parmi les fonctions de Pytorch , autograd est une fonction pour calculer la valeur de la différentielle
d’une fonction vectorielle \(\mathbf{F}(x)\) de plusieurs composantes, ici 2 composantes \(f(x),g(x)\).
On connaît la valeur \(\{F_i=(f_i,g_i)\}\) en N points \(\{x_i\}\), et on veut la valeur \(\{dF_i\}\) de la différentielle \(dF\) en ces N points dans une direction \(d\mathbf{l_i}=\{dlf_i, dlg_i \}\) fixée
Le résultat est un vecteur qui peut s’interpréter comme un produit vecteur-Jacobien (vector-Jacobian product) (attention ce n’est pas un produit classique matrice vecteur):
Pour effectuer le calcul numérique il est nécessaire de définir la valeur du vecteur: \(\mathbf{dl}_i=\{dlf_i, dlg_i\}\) (noté grad_output ou tensor_output). En fixant la valeur de \(\mathbf{dl}_i\), on choisit la combinaison linéaire des gradients des composantes de \(\mathbf{F}\). On note que la dimension de \(d\mathbf{l}_i\) est la même que celle de \(d\mathbf{F}_i\).
D’un point de vue performance, cela évite de calculer explicitement des matrices (jacobien), mais uniquement des vecteurs.
Si on a une fonction de plusieurs variables, on calcule séparément chacun des gradients par rapport à chacune des variables en utilisant cette procédure.
6.5.1. Interface autograd#
La classe autograd fournit 2 interfaces: torch.autograd.grad et torch.autograd.backward
torch.autograd.grad(outputs, inputs,grad_outputs): Calcule la somme des gradients des tenseurs de sortie (outputs) par rapport aux entrées (inputs).grad_inputsest le vecteur \(\mathbf{ds}\) dans le produit vecteur-Jacobien correspondant généralement aux gradients par rapport à chaque élément des tenseurs correspondants.torch.autograd.backward(tensors,grad_tensors): Calcule la somme des gradients des tenseurs (tensors) par rapport aux feuilles du graphe.grad_tensorsest le vecteur \(\mathbf{ds}\) dans le produit vecteur-Jacobien correspondant habituellement aux gradients par rapport à chaque élément des tenseurs correspondants.
En termes d’utilisation à haut niveau, on peut considérer torch.autograd.grad comme une fonction non mutable.
Comme mentionné dans la documentation, elle n’accumule pas les gradients dans l’attribut grad, mais renvoie directement les dérivées partielles calculées.
En revanche, torch.autograd.backward peut modifier les tenseurs en mettant à jour l’attribut grad des nœuds feuilles ; cette fonction ne renvoie aucune valeur.
En d’autres termes, cette dernière est plus adaptée au calcul des gradients pour un grand nombre de paramètres, comme dans les réseaux de neurones.
6.5.2. Exemple précédent : fonction d’une variable J(x)#
Etude de la fonction \(y(x) = x^3 + x^2 - 6x + 1\) sur [-3,3]
On connait la valeur de y : {\(y_i\)) en N points discrets {\(x_i\)}. On veut calculer la valeur du gradient en ces points , i.e. $\(\frac{\partial y_i}{\partial x_i} = (\frac{dy}{dx})(x=x_i)\)$
Pour cela autograd calcule la différentielle \({dy_i}\) en calculant le gradient \(\frac{\partial y_i}{\partial x_i}\)
à travers la relation:
Il faut donc choisir \(dx_i=1\)
import torch
X = np.linspace(-3,3,101)
Xt = torch.tensor(X, requires_grad=True)
Yt = Xt**3 + Xt**2 - 6*Xt + 1
dl = torch.ones_like(Yt)
Yt.backward(gradient=dl)
/home/buffat/venvs/jupyter/lib/python3.10/site-packages/torch/autograd/__init__.py:200: UserWarning: CUDA initialization: The NVIDIA driver on your system is too old (found version 9010). Please update your GPU driver by downloading and installing a new version from the URL: http://www.nvidia.com/Download/index.aspx Alternatively, go to: https://pytorch.org to install a PyTorch version that has been compiled with your version of the CUDA driver. (Triggered internally at ../c10/cuda/CUDAFunctions.cpp:109.)
Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
dYt = Xt.grad
# tracer
#plt.plot(Xt.detach().numpy(),dYt)
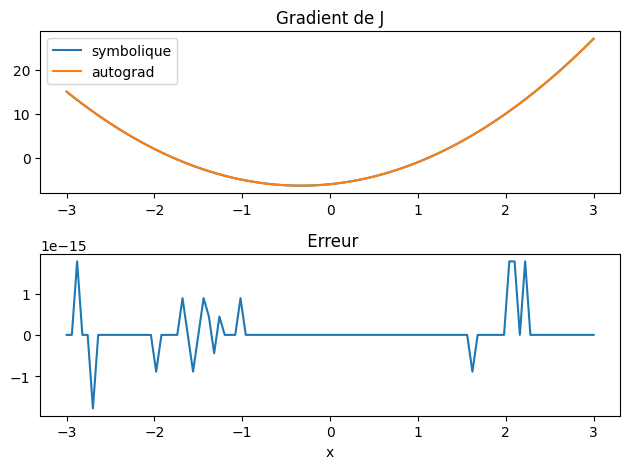
plt.subplot(2,1,1)
plt.plot(X,dJn(X),label="symbolique")
plt.plot(X,dYt,label="autograd")
plt.legend()
plt.title("Gradient de J")
plt.subplot(2,1,2)
plt.title(" Erreur")
plt.plot(X,dYt-dJ(X))
plt.xlabel("x")
plt.tight_layout()
6.5.3. Fonction vectorielle#
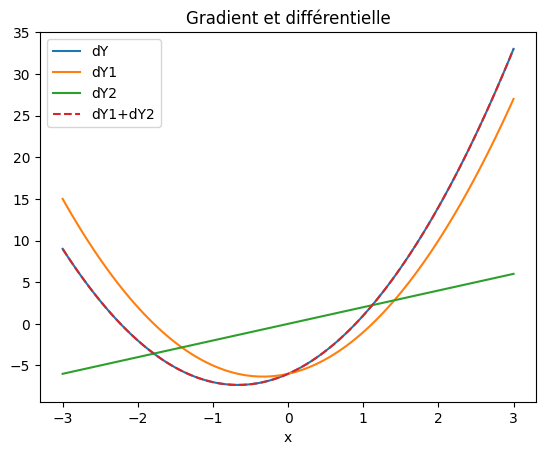
Si on considère maintenant une fonction vectorielle \(\mathbf{Y}\) de 2 composantes \(\{y1(x),y2(x)\}\) d’une variable x calculée en N points \(x_i\) dont on veut calculer la différentielle par rapport à x
\(x_i\) est un tableau de dimension N
\(Y_i\) est une matrice (N,2)
\(dl_i\) est une matrice (N,2) dont on choisit les valeurs suivant le résultat voulu.
pour \(dl_i = (1,1)\), on calcule la différentielle \(dY_i = \frac{dy1_i}{dx_i} + \frac{dy2_i}{dx_i}\)
pour \(dl_i = (1,0)\), on calcule la dérivée de \(y1\) : \(dY_i = \frac{dy1_i}{dx_i} \)
pour \(dl_i = (0,1)\), on calcule la dérivée de \(y2\) : \(dY_i = \frac{dy2_i}{dx_i} \)
Xt = torch.tensor(X, requires_grad=True)
Yt = torch.zeros(X.size,2)
Yt[:,0] = Xt**3 + Xt**2 - 6*Xt + 1
Yt[:,1] = Xt**2 - 2
Yt.shape
torch.Size([101, 2])
Xt = torch.tensor(X, requires_grad=True)
Yt = torch.zeros(X.size,2)
Yt[:,0] = Xt**3 + Xt**2 - 6*Xt + 1
Yt[:,1] = Xt**2 - 2
dl = torch.ones_like(Yt)
Yt.backward(gradient=dl)
dYt=Xt.grad
Xt = torch.tensor(X, requires_grad=True)
Yt = torch.zeros(X.size,2)
Yt[:,0] = Xt**3 + Xt**2 - 6*Xt + 1
Yt[:,1] = Xt**2 - 2
dl = torch.ones_like(Yt)
dl[:,1] = 0
Yt.backward(gradient=dl)
dY1=Xt.grad
Xt = torch.tensor(X, requires_grad=True)
Yt = torch.zeros(X.size,2)
Yt[:,0] = Xt**3 + Xt**2 - 6*Xt + 1
Yt[:,1] = Xt**2 - 2
dl = torch.ones_like(Yt)
dl[:,0] = 0
Yt.backward(gradient=dl)
dY2=Xt.grad
plt.plot(X,dYt,label="dY")
plt.plot(X,dY1,label="dY1")
plt.plot(X,dY2,label="dY2")
plt.plot(X,dY1+dY2,'--',label="dY1+dY2")
plt.xlabel("x")
plt.title("Gradient et différentielle")
plt.legend();
6.5.4. Fonction de plusieurs variables#
On calcule en N points \(\{x_i,y_i\}\) la fonction: $\(J(x,y) = xy + sin(x+y)\)$ dont on veut calculer les dérivées par rapport à x et à y
Pour cela on calcule la différentielle de J aux N points par rapport à x et par rapport à y. On a donc:
\(\{J_i\}\) vecteur de dimension N
\(\{X_i\}\) \(\{Y_i\}\) 2 vecteurs de dimension N
\(\{dl_i\}\) est un vecteur de dimension N t.q. \(dl_i = 1\)
le résultat est formé par 2 vecteur de dimension \(J^x_i\) le gradient par rapport à x et \(J^y_i\) le gradient par rapport à y
# choix des points ou on calcule la fonction
X = -2 + 4*np.random.rand(51)
Y = -2 + 4*np.random.rand(51)
Xt = torch.tensor(X, requires_grad=True)
Yt = torch.tensor(Y, requires_grad=True)
Jt = Xt*Yt + torch.sin(Xt-2*Yt)
# gradient exacte
dJdx = Y + np.cos(X-2*Y)
dJdy = X - 2*np.cos(X-2*Y)
Jt = Xt*Yt + torch.sin(Xt-2*Yt)
dl = torch.ones_like(Jt)
Jt.backward(gradient=dl)
# résultat
dJtdX = Xt.grad
dJtdY = Yt.grad
print(dJtdX)
print(dJtdY)
tensor([ 0.5550, 1.8130, -0.8148, 1.4389, -0.2557, -0.7858, -2.1723, -2.4152,
-0.9572, 0.4395, 1.2916, 1.3292, 1.4190, 0.8558, -1.9493, 0.4550,
-2.1161, -0.7197, 0.6085, -1.4084, -0.9989, -1.3635, 1.5993, 0.0561,
2.0993, 1.4868, 0.1865, 1.4797, -1.1229, 0.2147, -0.5247, 2.0398,
-2.6667, -0.2833, -0.1426, 0.5926, 0.6559, 1.9745, -2.6494, 1.6725,
-0.1961, 1.5417, 1.9207, -1.4361, 0.7349, -1.7003, -1.1152, -0.2386,
1.4934, 0.4516, 0.3202], dtype=torch.float64)
tensor([ 1.4350, -0.3795, -2.1855, -0.7779, -0.0128, 0.7128, 1.4053, 1.4250,
-1.1124, 0.7809, -1.2475, 2.6445, 1.0378, 1.5600, 3.3464, -1.2905,
2.8525, -1.4023, 1.3302, 1.3321, -1.9684, 1.0876, 2.2334, -2.1809,
0.2091, -0.8091, -3.6945, -0.3616, 0.2725, -3.4307, 1.1151, -2.5511,
1.9273, -1.4839, -0.7067, 2.1274, -0.5017, 0.7290, 1.9429, -0.6361,
-0.3612, 2.7556, 0.4144, -1.0417, -2.1266, 2.9824, 1.2989, -1.5634,
2.7351, -2.9288, 1.6154], dtype=torch.float64)
print("Erreur dJdx=",np.mean(dJdx - dJtdX.numpy()))
print("Erreur dJdy=",np.mean(dJdy - dJtdY.numpy()))
Erreur dJdx= 0.0
Erreur dJdy= 0.0
6.5.5. Avec l’interface autograd.grad#
Jt = Xt*Yt + torch.sin(Xt-2*Yt)
dl = torch.ones_like(Jt)
# resultat : 2 vecteurs
torch.autograd.grad(Jt,(Xt,Yt),dl,create_graph=True)
(tensor([ 0.5550, 1.8130, -0.8148, 1.4389, -0.2557, -0.7858, -2.1723, -2.4152,
-0.9572, 0.4395, 1.2916, 1.3292, 1.4190, 0.8558, -1.9493, 0.4550,
-2.1161, -0.7197, 0.6085, -1.4084, -0.9989, -1.3635, 1.5993, 0.0561,
2.0993, 1.4868, 0.1865, 1.4797, -1.1229, 0.2147, -0.5247, 2.0398,
-2.6667, -0.2833, -0.1426, 0.5926, 0.6559, 1.9745, -2.6494, 1.6725,
-0.1961, 1.5417, 1.9207, -1.4361, 0.7349, -1.7003, -1.1152, -0.2386,
1.4934, 0.4516, 0.3202], dtype=torch.float64,
grad_fn=<AddBackward0>),
tensor([ 1.4350, -0.3795, -2.1855, -0.7779, -0.0128, 0.7128, 1.4053, 1.4250,
-1.1124, 0.7809, -1.2475, 2.6445, 1.0378, 1.5600, 3.3464, -1.2905,
2.8525, -1.4023, 1.3302, 1.3321, -1.9684, 1.0876, 2.2334, -2.1809,
0.2091, -0.8091, -3.6945, -0.3616, 0.2725, -3.4307, 1.1151, -2.5511,
1.9273, -1.4839, -0.7067, 2.1274, -0.5017, 0.7290, 1.9429, -0.6361,
-0.3612, 2.7556, 0.4144, -1.0417, -2.1266, 2.9824, 1.2989, -1.5634,
2.7351, -2.9288, 1.6154], dtype=torch.float64,
grad_fn=<AddBackward0>))
