TP célérité d’un choc par machine learning

9.5. TP célérité d’un choc par machine learning#

Marc BUFFAT, dpt mécanique, UCB Lyon 1

tube a choc

modèle

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
import sklearn as sk
from sklearn.model_selection import train_test_split
from sklearn.ensemble import RandomForestRegressor
from sklearn.metrics import r2_score

def plot_data(P1,RHO1,P2,RHO2,SS,CS,EFTS,EFHS):
    plt.figure(figsize=(14,6))
    plt.subplot(1,2,1)
    plt.plot(P2/P1,label="pression",lw=2)
    plt.plot(RHO2/RHO1,'--',label="densité",lw=2)
    plt.legend()
    plt.xlabel("mesure")
    plt.title("rapport pression et densité")
    plt.subplot(1,2,2)
    plt.plot(SS,label="choc",lw=2)
    plt.plot(CS,label="contacte",lw=2)
    plt.plot(EFTS, label="détente",lw=2)
    plt.legend()
    plt.xlabel("mesure")
    plt.title("célérité des ondes");
    return
def plotY(y_test,ypred,titre=""):
    plt.scatter(y_test[:],ypred[:])
    x1 = np.linspace(np.min(y_test[:]),np.max(y_test[:]),51)
    plt.plot(x1,x1,'--r',lw=2,label="optimal")
    plt.legend()
    plt.title(f"prediction {titre}")
    plt.xlabel("mesures")
    plt.ylabel("predictions")
    plt.axis('equal');
    return
def celerite_plot(X,y,ypred):
    plt.scatter(X,y,label='mesure')
    plt.plot(X,ypred,'or',label='prediction')
    plt.legend()
    plt.xlabel("rapport HP/BP")
    plt.title("célerité des ondes")
    return

9.5.1. Principe du machine learning#

problème : prédire une loi \(\mathcal{F}\)

\[ Y = \mathcal{F}(\textbf{X}) \]

à partir de l’apprentissage à l’aide d’une base de données de test \(\textbf{X}_i, Y_i\)

\(\rightarrow\) Problème de minimisation

Trouver la meilleur approximation \(\mathbf{F}\) minimisant l’erreur \(J\) sur la base de données d’apprentissage. \(J\) est une fonction coût du type:

\[ J = \sum_i \alpha_i || \mathbf{F}(\mathbf{X}_i) - Y_i ||^2 \]

  • \(\mathbf{F}(\mathbf{X}_i)\) est fonction d’une combinaison linéaire des données $\(\mathbf{F}(\mathbf{X}_i) = \mathbf{F}\left(\sum_j \beta_j \mathbf{X}_{i,j}\right)\)$

  • pas de forme explicite pour \(\mathbf{F}\) qui dépend de très nombreux paramètres à déterminer par une méthode de minimisation (de type gradient)

  • aucune méthode universelle

\(\rightarrow\) Algorithme implicite nécessitant des données annotées (i.e. avec le résultat) pour l’apprentissage et les tests de validation (apprentissage supervisée)

  • Random Forest Algorithm

Par définition, un Random Forest a besoin de trois hyper-paramètres principaux (paramètres fixes), qui doivent être définis avant l’entraînement. Il s’agit notamment de la taille des arbres (le nombre de nœuds maximal), du nombre d’arbres à utiliser et le nombre de caractéristiques échantillonnées (nombre de variables aléatoires choisies à chaque mélange depuis les variables explicatives). À partir de là, le modèle peut être utilisé pour résoudre les problèmes de régression ou de classification.

9.5.2. Lecture de la base de données expérimentales#

  • conditions expérimentales \(p_1\), \(\rho_1\), \(p_2\), \(\rho_2\)

  • mesures (célérité)

    • choc ss

    • contacte cs

    • détentes efts efhs

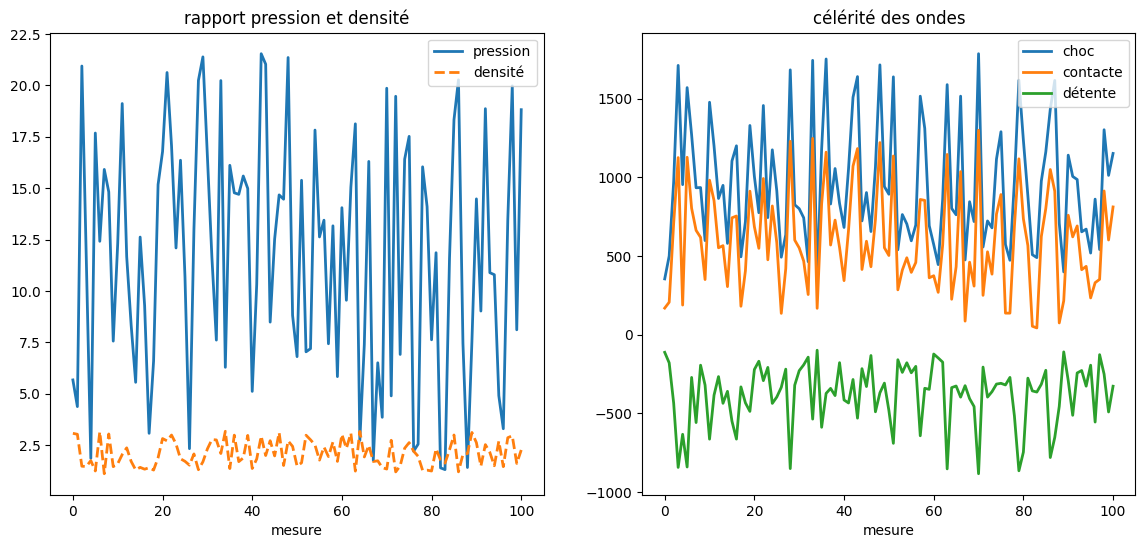
# lecture des données
P1, RHO1, P2, RHO2, SS, SC, EFTS, EFHS = np.loadtxt('choc_db.dat',unpack=True)
plot_data(P1,RHO1,P2,RHO2,SS,SC,EFTS,EFHS)

9.5.3. Apprentissage sur les données brutes#

création des tableaux X (données) y (résultats) puis split en training et test

# préparation des données pour le machine learning
X = None; y = None; X_train = None; Y_train = None; X_test = None; y_test = None
### BEGIN SOLUTION
### END SOLUTION
print("taille des données:",X.shape,y.shape)
print("entrainement / test:",X_train.shape,X_test.shape)

# machine learning
clf = RandomForestRegressor(max_depth=None, random_state=0, n_estimators=100, criterion='squared_error')
cfl = clf.fit(X_train, y_train)
print("score apprentissage = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred  = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score (prediction) = {:.2f}".format(r2))

plt.figure(figsize=(14,6))
plt.subplot(1,2,1)
plotY(y_test,ypred,"random forest")
plt.subplot(1,2,2)
celerite_plot(X_test[:,2]/X_test[:,0],y_test,ypred)

9.5.4. apprentissage / au rapport de pression et densité#

# préparation des données pour le machine learning
X = None; y = None; X_train = None; Y_train = None; X_test = None; y_test = None
### BEGIN SOLUTION
### END SOLUTION
print("taille des données:",X.shape,y.shape)
print("entrainement / test:",X_train.shape,X_test.shape)

# machine learning
clf = RandomForestRegressor(max_depth=None, random_state=0, n_estimators=100, criterion='squared_error')
cfl = clf.fit(X_train, y_train)
print("score apprentissage = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred  = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score (prediction) = {:.2f}".format(r2))

plt.figure(figsize=(14,6))
plt.subplot(1,2,1)
plotY(y_test,ypred,"random forest")
plt.subplot(1,2,2)
celerite_plot(X_test[:,0],y_test,ypred)

9.5.5. apprentissage sur les données sans dimension#

# préparation des données pour le machine learning
X = None; y = None; X_train = None; Y_train = None; X_test = None; y_test = None
### BEGIN SOLUTION
### END SOLUTION
print("taille des données:",X.shape,y.shape)
print("entrainement / test:",X_train.shape,X_test.shape)

# machine learning
clf = RandomForestRegressor(max_depth=None, random_state=0, n_estimators=100, criterion='squared_error')
cfl = clf.fit(X_train, y_train)
print("score apprentissage = {:2d}%".format(int(100*clf.score(X_train, y_train))))
ypred  = clf.predict(X_test)
r2 = r2_score(y_test, ypred)
print("R2 score (prediction) = {:.2f}".format(r2))

plt.figure(figsize=(14,6))
plt.subplot(1,2,1)
plotY(y_test,ypred,"random forest")
plt.subplot(1,2,2)
celerite_plot(X_test[:,0],y_test,ypred)

9.5.6. Questions#

  • dépendance aux données

  • apport du machine learning

  • intelligence artificiel ?

  • modèle explicatif ?

9.5.7. FIN#

from platform import python_version

print("Python version:",python_version())
print("numpy version:",np.__version__)
print("skit learn version:",sk.__version__)
Contenu