2. Simulation d’EDO en Python#
Marc BUFFAT, Université Claude Bernard Lyon 1
%matplotlib inline
# bibliotheques de base
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
from IPython.core.display import HTML
2.1. EDO du 1er ordre#
Soit l’EDO
2.1.1. Méthode d’Euler#
2.1.1.1. programmation#
mise sous forme générique
paramètres :
fonction \(f(y,t)\),
C.I. \(y_0\),
temps final \(t_f\)
pas en temps \(dt\)
calcul itératif
à \(t^{n+1}= t^n + dt\)
analyse de la précision
calcul solution pour différents \(dt=1,0.1,0.01\)
calcul de l’erreur avec \(y_e=e^{at}\)
comportement pour différentes valeurs de \(a=0.2,1,2\)
2.1.1.2. fonction générique Euler#
écriture d’une fonction générique dépendant des paramètres
def Euler(f,y0,tf,dt):
# implementation méthode d'Euler
def Euler(f,y0,tf,dt):
"""Integration de dy/dt=f(y,t) par Euler
avec une CI y0 pendant tf avec un pas dt"""
n = int(tf/dt)
T = np.zeros(n+1)
Y = np.zeros(n+1)
Y[0] = y0
T[0] = 0.0
for i in range(n):
Y[i+1] = Y[i] + dt*f(Y[i],T[i])
T[i+1] = T[i] + dt
return Y,T
2.1.1.3. calcul 2nd membre: fonction F(y,t)#
définition de la fonction second membre
def F(y,t):
# second membre
def F(y,t):
"""2nd membre de l'EDO"""
global a
return a*y
2.1.1.4. trace la solution pour dt=1,0.1,0.01 et l’erreur:#
def tracesol(T1,Y1,T2,Y2,T3,Y3,titre):
def tracesol(T1,Y1,T2,Y2,T3,Y3,titre):
"""trace solution et erreur"""
plt.figure(figsize=(12,5))
plt.subplot(1,2,1)
plt.title(titre)
plt.plot(T1,Y1,'<-',label="dt=1")
plt.plot(T2,Y2,'^-',label="dt=0.1")
plt.plot(T3,Y3,'+-',label="dt=0.01")
plt.legend()
plt.subplot(1,2,2)
plt.title("erreur relative |(uex-uh)/uex|")
plt.semilogy(T1,np.abs(Y1-np.exp(a*T1))/np.exp(a*T1),label="Err1")
plt.semilogy(T2,np.abs(Y2-np.exp(a*T2))/np.exp(a*T2),label="Err2")
plt.semilogy(T3,np.abs(Y3-np.exp(a*T3))/np.exp(a*T3),label="Err3")
plt.legend()
return
2.1.1.5. Application#
résolution avec différents dt et tracer de l’évolution de l’erreur
avec a=0.2 (facile) ou a=2.0 (cas difficile)
a=0.2 # cas facile
a=2.0 # cas difficile
# solution Euler
tf=5
y0=1.0
Y1,T1 = Euler(F,y0,tf,1.)
Y2,T2 = Euler(F,y0,tf,0.1)
Y3,T3 = Euler(F,y0,tf,0.01)
tracesol(T1,Y1,T2,Y2,T3,Y3,'Euler')
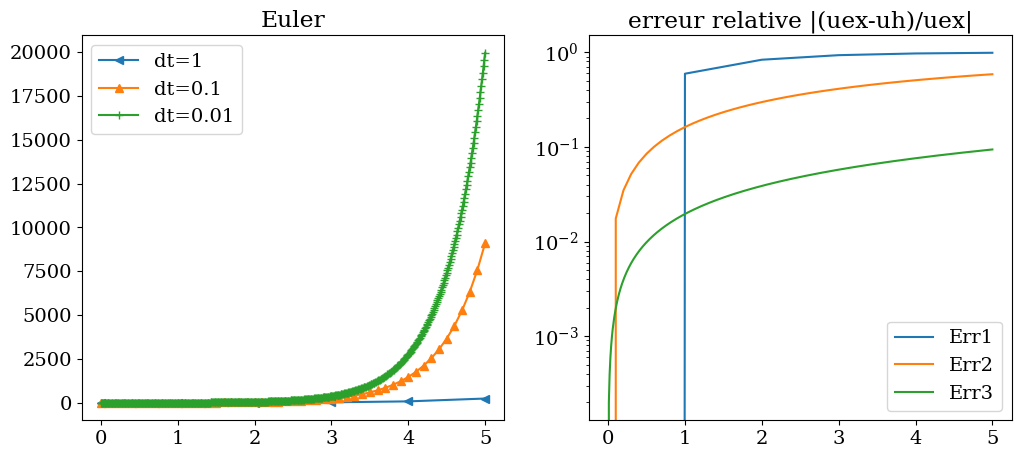
On constate que la méthode d’Euler est une méthode peu précise avec une accumulation d’erreur au cours du temps, dû à sa précision d’ordre 1. La décroissance de l’erreur en fonction de \(dt\) est bien d’ordre 1 (sur la figure de droite, décroissance d’un facteur \(10^1\) pour un \(dt\) divisé par \(10\))
2.1.2. Méthode RungeKutta ordre 2#
2.1.2.1. fonction générique RK2#
def RK2(f,y0,tf,dt)
# implementation méthode RK2
def RK2(f,y0,tf,dt):
"""Integration de dy/dt=f(y,t) par Runge Kutta 2
avec une CI y0 pendant tf avec un pas dt"""
n = int(tf/dt)
T = np.zeros(n+1)
Y = np.zeros(n+1)
Y[0] = y0
T[0] = 0.0
for i in range(n):
K1 = f(Y[i],T[i])
K2 = f(Y[i]+K1*dt,T[i]+dt)
Y[i+1] = Y[i] + (K1+K2)*dt/2.
T[i+1] = T[i] + dt
return Y,T
2.1.2.2. Application#
résolution avec différents dt et tracer de l’évolution de l’erreur
# solution RK2
tf=5
y0=1.0
Y1,T1 = RK2(F,y0,tf,1.)
Y2,T2 = RK2(F,y0,tf,0.1)
Y3,T3 = RK2(F,y0,tf,0.01)
# tracer solution et erreur
tracesol(T1,Y1,T2,Y2,T3,Y3,"RK2")
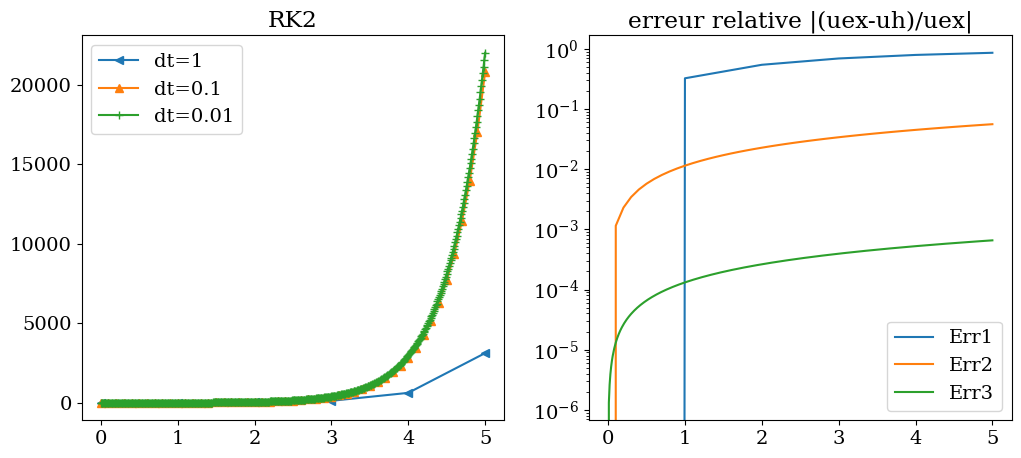
On constate que la solution est bien plus précise qu’avec la méthode d’Euler. La décroissance de l’erreur en fonction de \(dt\) est bien d’ordre 2 (sur la figure de droite, décroissance d’un facteur \(10^2\) pour un \(dt\) divisé par \(10\))
2.1.3. Méthode RungeKutta ordre 4#
2.1.3.1. fonction générique RK4#
def RK4(f,y0,tf,dt)
# implementation méthode RK4
def RK4(f,y0,tf,dt):
"""Integration de dy/dt=f(y,t) par Runge Kutta 4
avec une CI y0 pendant tf avec un pas dt"""
n = int(tf/dt)
T = np.zeros(n+1)
Y = np.zeros(n+1)
Y[0] = y0
T[0] = 0.0
for i in range(n):
K1 = f(Y[i],T[i])
K2 = f(Y[i]+K1*dt/2,T[i]+dt/2)
K3 = f(Y[i]+K2*dt/2,T[i]+dt/2)
K4 = f(Y[i]+K3*dt ,T[i]+dt)
Y[i+1] = Y[i] + (K1+2*K2+2*K3+K4)*dt/6
T[i+1] = T[i] + dt
return Y,T
2.1.3.2. Application#
résolution avec différents dt et tracer de l’évolution de l’erreur
# solution RK4
tf=5
y0=1.0
Y1,T1 = RK4(F,y0,tf,1.)
Y2,T2 = RK4(F,y0,tf,0.1)
Y3,T3 = RK4(F,y0,tf,0.01)
# tracer solution et erreur
tracesol(T1,Y1,T2,Y2,T3,Y3,"RK4")
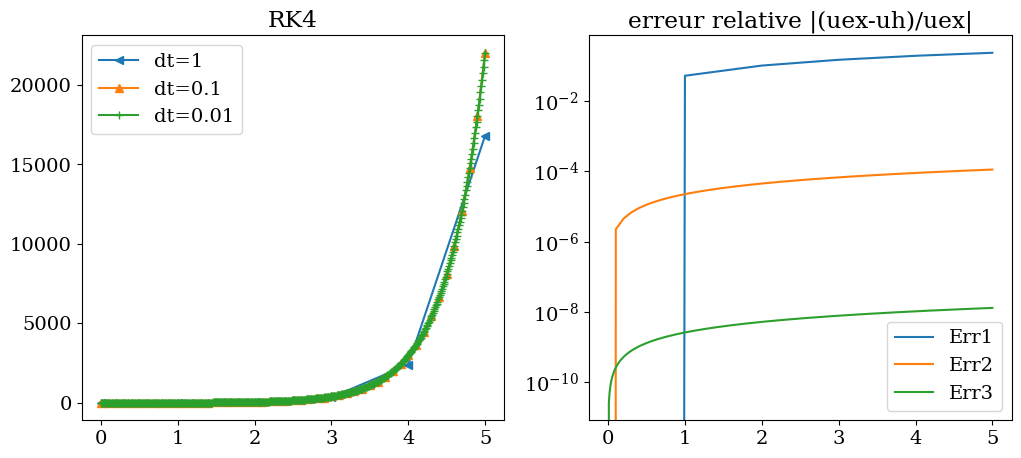
On constate que la solution est très précise mais avec de grand \(dt\). La décroissance de l’erreur en fonction de \(dt\) est bien d’ordre 4 (sur la figure de droite, décroissance d’un facteur \(10^4\) pour un \(dt\) divisé par \(10\))
2.1.4. Méthode implicite#
EDO $\( \frac{dy}{dt} = f(y,t) \)$
schema implicite en temps $\( \frac{y^{n+1}-y^n}{\Delta t} = f(y^{n+1},t^{n+1}) \)$
problème non linéaire pour \( \Delta y = y^{n+1}-y^n \)
DL a l’ordre 1 avec la jacobienne \(\frac{df}{dy}\)
généralisation avec un schema RK2 implicite
2.1.4.1. Calcule de la jacobienne \(df/dy\)#
def dF(y,t):
global a
return a
2.1.4.2. Implementation RK2 implicite#
calcul \(\Delta y\) avec \(f(t_{n+1},y_{n+1})\) par DL avec \(\Delta y = y_{n+1}-y_n \)
#
def RK2i(f,y0,tf,dt):
"""Integration de dy/dt=f(y,t) par Runge Kutta 2 implicite
avec une CI y0 pendant tf avec un pas dt"""
n = int(tf/dt)
T = np.zeros(n+1)
Y = np.zeros(n+1)
Y[0] = y0
T[0] = 0.0
for i in range(n):
K1 = f(Y[i],T[i])
DY = K1 / (1./dt - dF(Y[i],T[i]))
K2 = f(Y[i]+DY,T[i]+dt)
Y[i+1] = Y[i] + (K1+K2)*dt/2.
T[i+1] = T[i] + dt
return Y,T
2.1.4.3. Application (cas raide et non raide)#
a=0.2 ou a= 2.0
print("a=",a)
# solution RK2i
tf=5
y0=1.0
Y1,T1 = RK2i(F,y0,tf,1.)
Y2,T2 = RK2i(F,y0,tf,0.1)
Y3,T3 = RK2i(F,y0,tf,0.01)
# tracer solution et erreur
tracesol(T1,Y1,T2,Y2,T3,Y3,"RK2i")
a= 2.0
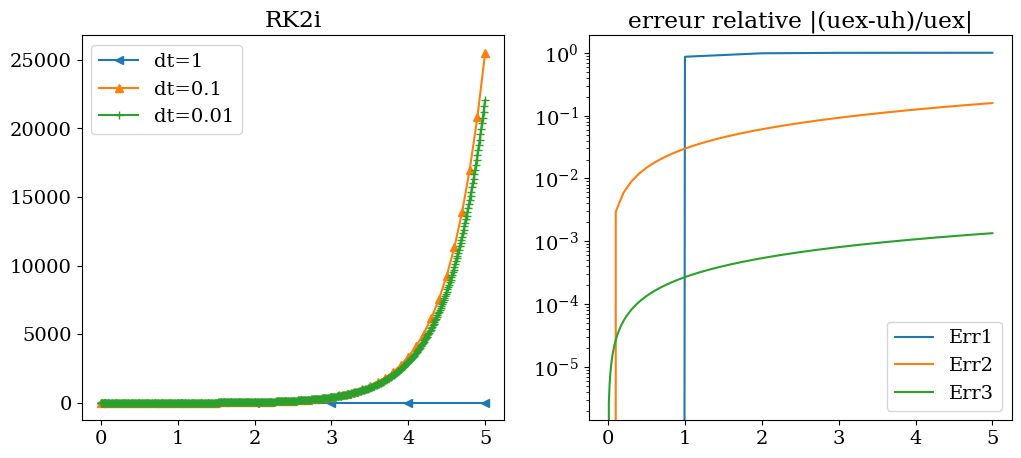
La décroissance de l’erreur en fonction de \(dt\) est bien d’ordre 2 (sur la figure de droite, décroissance d’un facteur \(10^2\) pour un \(dt\) divisé par \(10\)). Par contre, cette méthode n’apporte rien dans ce cas-là par rapport à une méthode RK2 explicite.
2.2. Bibliothèque Scipy (méthode la plus complete)#
dans scipy.integrate ode (version objet)
dopri5 RK4-5
dopri853 RK8
vode implicite Adams (non raide) et BDF (raide)
lsoda Adams Bashford et BDF
calcul automatique du pas en temps pour conserver une précision fixée
attention à l’ordre des arguments pour F
2.2.1. définition du 2nd membre (pour integrate.ode)#
ncount = 0
def FF(t,y,a):
"""2nd membre de l'EDO"""
global ncount
ncount += 1
return a*y
2.2.2. Implementation solveODE#
interface avec integrate.ode
cas facile et difficile
# solve with integrate.ode
from scipy import integrate
# cas de calcul (facile / difficile)
a = 0.2
a = 2.0
def solveODE(F,y0,tf,dt,methode):
"""integration avec ode """
global ncount,a
ncount = 0
# parametre
n = int(tf/dt)
T = np.linspace(0,tf,n+1)
Y = np.zeros(n+1)
Y[0] = y0
solver = integrate.ode(F, jac=None).set_integrator(methode)
solver.set_initial_value(y0, T[0]).set_f_params(a)
for i in range(1,n+1):
if solver.successful():
Y[i]=solver.integrate(T[i])
else:
print("Erreur ODE")
exit
print("SolveODE a={}: nbre de calcul de F = {}".format(a,ncount))
return Y,T
2.2.3. Application: schema RK ordre 4-5#
tf=5
y0=1.0
Y1,T1 = solveODE(FF,y0,tf,1.,'dopri5')
Y2,T2 = solveODE(FF,y0,tf,0.1,'dopri5')
Y3,T3 = solveODE(FF,y0,tf,0.01,'dopri5')
# tracer solution et erreur
tracesol(T1,Y1,T2,Y2,T3,Y3,"RK5")
/tmp/ipykernel_649749/263263876.py:19: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
Y[i]=solver.integrate(T[i])
SolveODE a=2.0: nbre de calcul de F = 312
SolveODE a=2.0: nbre de calcul de F = 657
SolveODE a=2.0: nbre de calcul de F = 3501
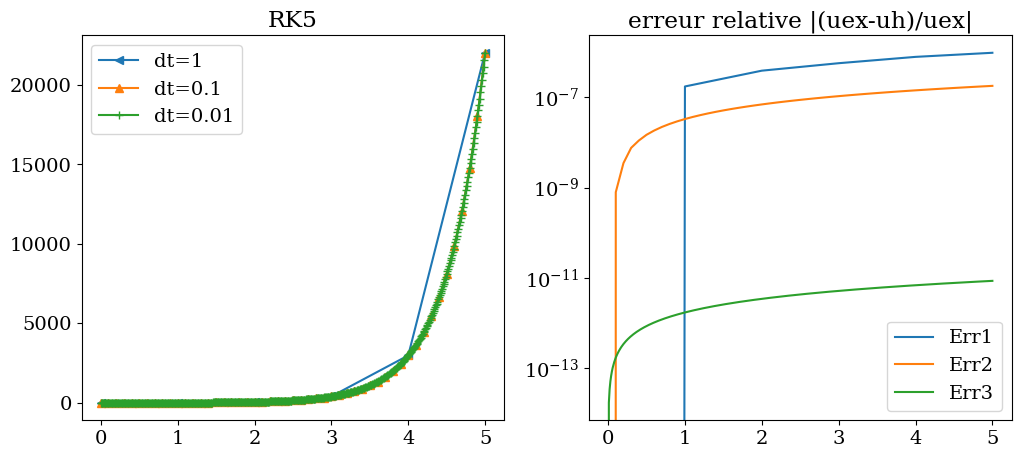
On constate que l’utilisation de la bibliothèque scipy ode permet d’obtenir la solution la plus précise, car contrairement aux méthodes programmées précédemment, la fonction ode utilise un ajustement automatique du pas en temps en calculant à chaque pas en temps 2 approximations de la solution : une avec une méthode RK4 et une avec une méthode RK5, ce qui permet d’ajuster l’erreur d’intégration et de la maintenir en dessous d’un critère (ici \(10^{-6}\)) quelque que soit le pas en temps choisit pour avoir la solution. Attention, ce pas en temps ne correspond pas au pas d’intégration, mais au pas où on veut obtenir la solution.
2.2.4. Application: schema RK ordre 8#
la méthode la plus précise
Y1,T1 = solveODE(FF,y0,tf,1.,'dop853')
Y2,T2 = solveODE(FF,y0,tf,0.1,'dop853')
Y3,T3 = solveODE(FF,y0,tf,0.01,'dop853')
# tracer solution et erreur
tracesol(T1,Y1,T2,Y2,T3,Y3,"RK8")
/tmp/ipykernel_649749/263263876.py:19: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
Y[i]=solver.integrate(T[i])
SolveODE a=2.0: nbre de calcul de F = 149
SolveODE a=2.0: nbre de calcul de F = 740
SolveODE a=2.0: nbre de calcul de F = 7001
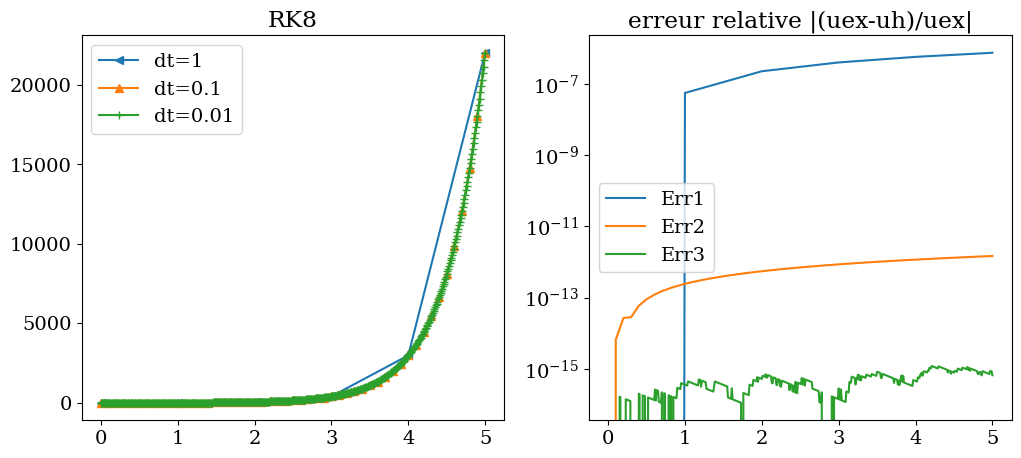
2.2.5. Application: schema implicite Adams Bashford#
Y1,T1 = solveODE(FF,y0,tf,1.,'vode')
Y2,T2 = solveODE(FF,y0,tf,0.1,'vode')
Y3,T3 = solveODE(FF,y0,tf,0.01,'vode')
# tracer solution et erreur
tracesol(T1,Y1,T2,Y2,T3,Y3,"Adams bashford")
/tmp/ipykernel_649749/263263876.py:19: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
Y[i]=solver.integrate(T[i])
SolveODE a=2.0: nbre de calcul de F = 108
SolveODE a=2.0: nbre de calcul de F = 108
SolveODE a=2.0: nbre de calcul de F = 108
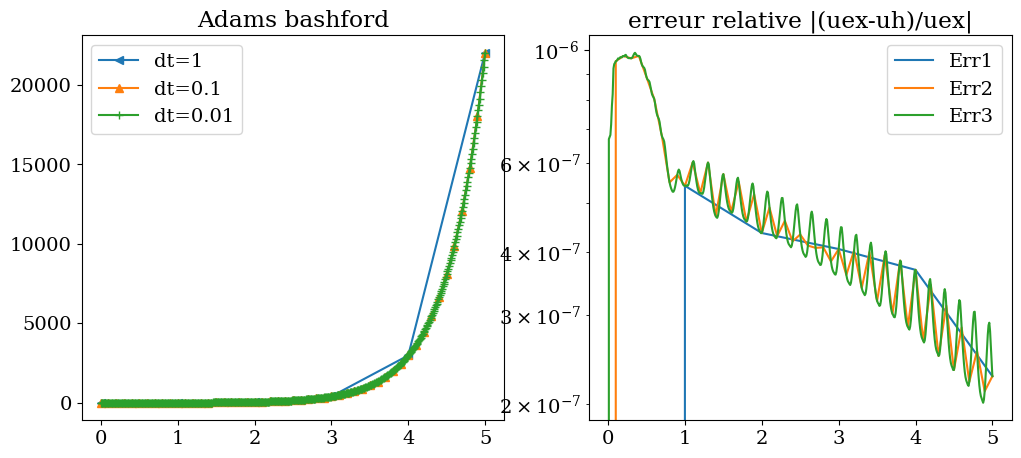
On constate que cette méthode couplée permet d’obtenir une erreur quasiment indépendante du pas en temps, mais qui est un peu moins bonne qu’avec RK45
2.3. Bibliothèque Scipy (méthode la plus simple)#
odeint dans scipy.integrate
la méthode la plus simple a utilisée
utilise la bibliotheque lsoda
adams bashford pour les cas non raides
BDF dans les cas raides
2.3.1. Implémentation#
# second membre
ncount = 0
def F(y,t,a):
"""2nd membre de l'EDO"""
global ncount
ncount += 1
return a*y
from scipy.integrate import odeint
# cas de calcul (facile / difficile)
a = 0.2
a = 2.0
# parametres
n=5
ncount = 0
T1 = np.linspace(0,tf,n+1)
Y1 = odeint(F,y0,T1,args=(a,))
print("Nbre de calcul de F = {}".format(ncount))
ncount = 0
T2 = np.linspace(0,tf,10*n+1)
Y2 = odeint(F,y0,T2, args=(a,))
print("Nbre de calcul de F = {}".format(ncount))
ncount = 0
T3 = np.linspace(0,tf,100*n+1)
Y3 = odeint(F,y0,T3,args=(a,))
print("Nbre de calcul de F = {}".format(ncount))
# trace
tracesol(T1,Y1[:,0],T2,Y2[:,0],T3,Y3[:,0],'odeint')
Nbre de calcul de F = 171
Nbre de calcul de F = 171
Nbre de calcul de F = 171
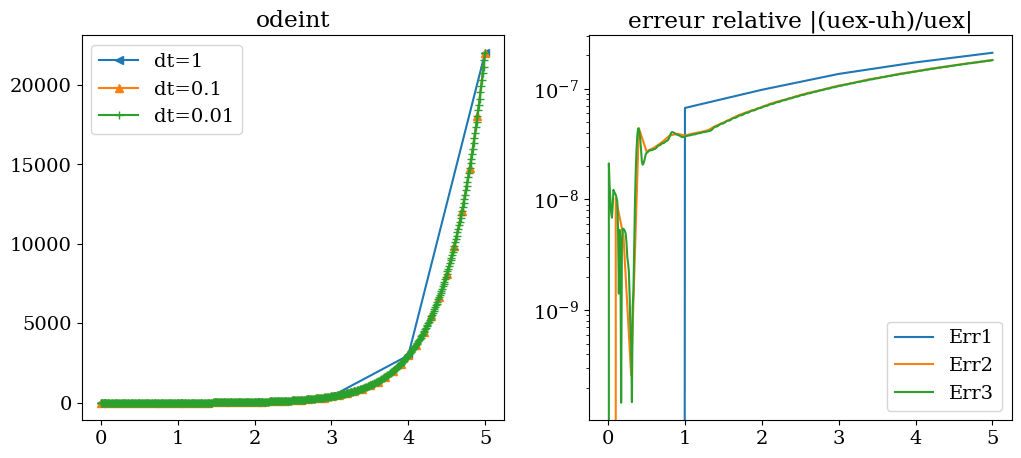
On constate que odeint permet d’obtenir une erreur quasiment indépendante du pas en temps de l’ordre de \(10^{-7}\), mais qui est un peu moins bonne qu’avec RK45
2.3.2. avec un contrôle de la précision#
tol=1.0e-12
n=5
ncount = 0
T1 = np.linspace(0,tf,n+1)
Y1 = odeint(F,y0,T1,args=(a,),rtol=tol,atol=tol)
print("Nbre de calcul de F = {}".format(ncount))
ncount = 0
T2 = np.linspace(0,tf,10*n+1)
Y2 = odeint(F,y0,T2,args=(a,),rtol=tol,atol=tol)
print("Nbre de calcul de F = {}".format(ncount))
ncount = 0
T3 = np.linspace(0,tf,100*n+1)
Y3 = odeint(F,y0,T3,args=(a,),rtol=tol,atol=tol)
print("Nbre de calcul de F = {}".format(ncount))
# trace
tracesol(T1,Y1[:,0],T2,Y2[:,0],T3,Y3[:,0],"odeint")
Nbre de calcul de F = 304
Nbre de calcul de F = 304
Nbre de calcul de F = 302
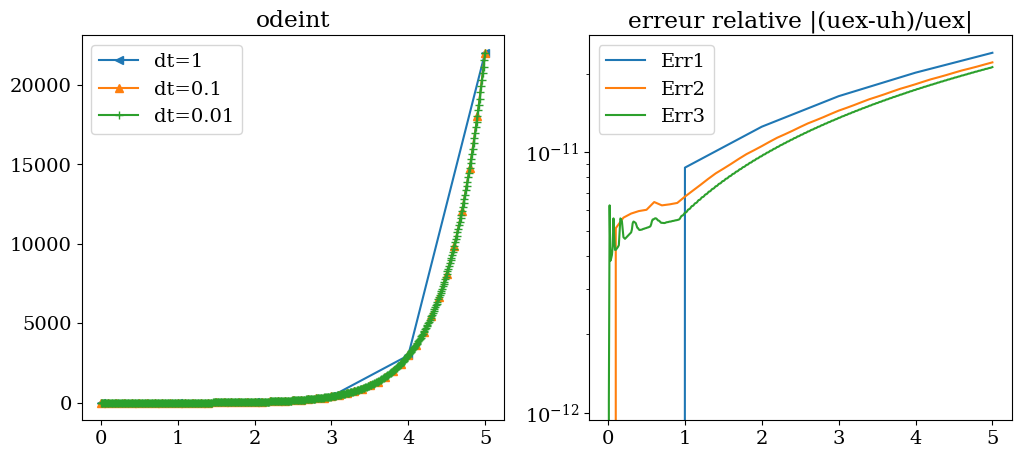
C’est ce que l’on vérifie en imposant une précision plus grande \(10^{-12}\) qui permet d’obtenir une erreur de l’ordre de \(10^{-11}\) quel que soit \(dt\)
2.3.3. Choix des méthodes#
Pour résoudre une EDO, utilisation des fonctions de la bibliothèque scipy
pble simple : odeint
pble complexe: ode
attention à la précision par défaut
2.3.4. Application: modélisation d’une population#
avec \(a\) le taux de reproduction et \(\sin \omega t\) modélise la variation de nourriture au cours du temps avec une periode \(T = 2\pi/\omega \)
A.N: \(a=0.01\) et \(\omega = 2\pi/365\), et t en jours
def F(y,t,a,omega):
return a*y*(1+np.sin(omega*t))
2.3.4.1. Simulation#
# parametres
a=0.01
omega=2*np.pi/365.
# solution
y0=4
T=np.linspace(0,365.0,100)
Y=odeint(F,y0,T,args=(a,omega))
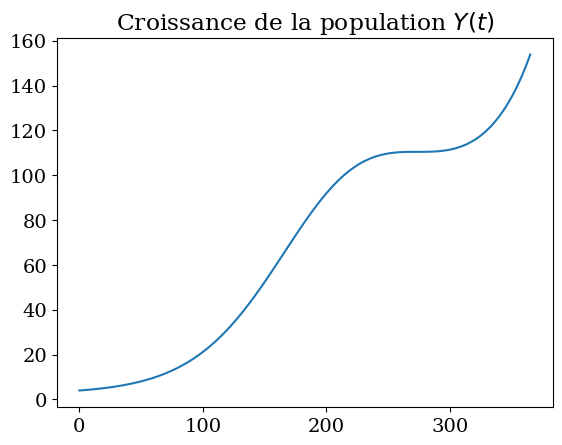
plt.plot(T,Y[:,0])
plt.title("Croissance de la population $Y(t)$")
Text(0.5, 1.0, 'Croissance de la population $Y(t)$')
2.3.4.2. Analyse de la solution#
au bout de combien de jours la population a-t-elle été multipliée par 10 ?
out=np.where(np.abs(Y-10*y0) < 1.)
i=out[0][0]
print(" Réponse à t = {:.2f} Y={:.2f} ~ 10*y0 avec y0={}".format(T[i],Y[i,0],Y[0]))
Réponse à t = 132.73 Y=39.44 ~ 10*y0 avec y0=[4.]
2.4. Généralisation: Equations d’ordre > 1#
Equations différentielles d’ordre n :
Transformation en un système d’EDO du \(1^{er}\) ordre:
2.4.1. Exemple: pendule simple#
soit un pendule de masse \(m\) et longueur \(l\) qui fait un angle \(\theta(t)\) avec la verticale
En formulation de Lagrange on a \(L=T-U\) avec
Les équations de Lagrange :
s’écrivent:
2.4.1.1. oscillateur harmonique#
Dans le cas de petites ocillations \(y=\theta \ll 1\), on a un oscillateur harmonique de pulsation \(\omega=\sqrt{k/M}\)
Forme EDO du 1er ordre
conditions initiales
solution analytique
2.4.2. definition du 2nd membre: cas linéaire et non linéaire#
# oscillateur harmonique
def Fl(Y,t,omega):
"""second membre linearise EDO"""
return np.array([Y[1],-omega**2*Y[0]])
# cas non lineaire
def F(Y,t,omega):
"""second membre NL"""
return np.array([Y[1],-omega**2*np.sin(Y[0])])
2.4.3. Application: : comparaison solution linéaire et non linéaire#
# parametres
L=1.0
g=10.0
omega=np.sqrt(g/L)
# integration sur 5 périodes
tmax = 5.*2*np.pi/omega
t = np.linspace(0,tmax,100)
Y0 = np.array([np.pi/5,0.])
Yl = odeint(Fl,Y0,t,args=(omega,))
Y = odeint(F,Y0,t,args=(omega,))
thetal=Yl[:,0]
theta =Y[:,0]
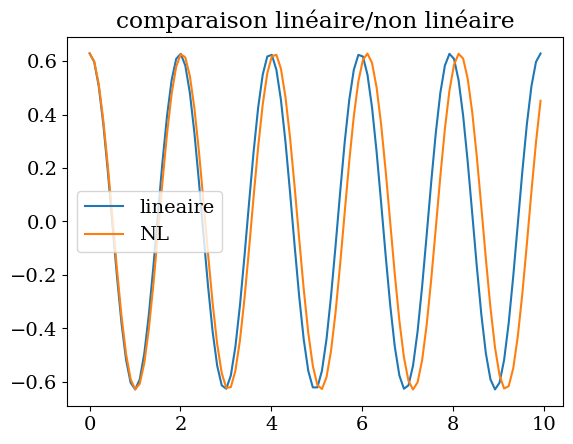
plt.plot(t,thetal,label="lineaire")
plt.plot(t,theta ,label="NL")
plt.legend()
plt.title("comparaison linéaire/non linéaire")
Text(0.5, 1.0, 'comparaison linéaire/non linéaire')
2.5. Système raide#
un système d’EDO est dit raide si certaines méthodes d’intégration (en général explicite) deviennent instables ou nécessitent des pas d’intégration excessivement petits (stiff ODE)
2.5.1. premier exemple#
On considère l’EDO non linéaire suivante:
Cette EDO due à Larry Shampine modélise l’évolution du rayon \(y(t)\) de la flamme d’une allumette qui croit rapidement pour atteindre une valeur critique qui dépend de la surface \(y^2\) et du volume \(y^3\) de la flamme et d’un paramêtre critique \(\delta\) qui est petit. Le temps d’évolution du système est de l’ordre de \(2/\delta\).
Cette EDO admet une solution analytique en fonction de la fonction de Lambert \(W(t)\), qui est une fonction spéciale non analytique:
2.5.1.1. cas non raide \(\delta=10^{-2}\)#
résolution explicite classique
from time import time
# nbre d'appel de F
ncal = 0
npas = 0
def FF(t,U):
global ncal
ncal += 1
return U**2*(1-U)
def solout(t,U):
global npas
npas += 1
return
# parametres
s = 10**2-1
N = 100
T = np.linspace(0,2*(s+1.),N)
# solution exacte
from scipy.special import lambertw
Uex = 1./np.real(1.+lambertw(s*np.exp(s)*np.exp(-T)))
# CI
U0=1./(s+1.)
# integration RK4
debut = time()
solver = integrate.ode(FF, jac=None).\
set_integrator('dopri5',atol=1.e-5, rtol = 1.e-4, verbosity = True)
solver.set_solout(solout)
t=0.0
solver.set_initial_value(U0, t)
UU = np.zeros(N)
UU[0]=U0
for i in range(1,N):
if solver.successful():
UU[i]=solver.integrate(T[i])
else:
print("Erreur ODE")
exit
cpu = time() - debut
print("cpu:",cpu)
print("nombre de pas en temps: ",npas)
print("nombre de calcul de F : ",ncal)
cpu: 0.00436854362487793
nombre de pas en temps: 207
nombre de calcul de F : 754
/tmp/ipykernel_649749/3692709467.py:33: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
UU[i]=solver.integrate(T[i])
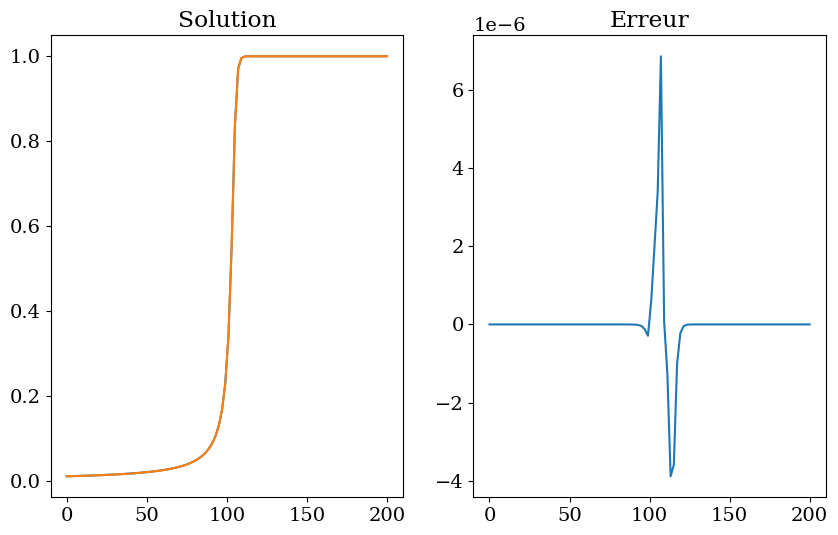
plt.figure(figsize=(10,6))
plt.subplot(1,2,1)
plt.plot(T,UU)
plt.plot(T,Uex)
plt.title("Solution")
plt.subplot(1,2,2)
plt.plot(T,UU-Uex)
plt.title("Erreur")
Text(0.5, 1.0, 'Erreur')
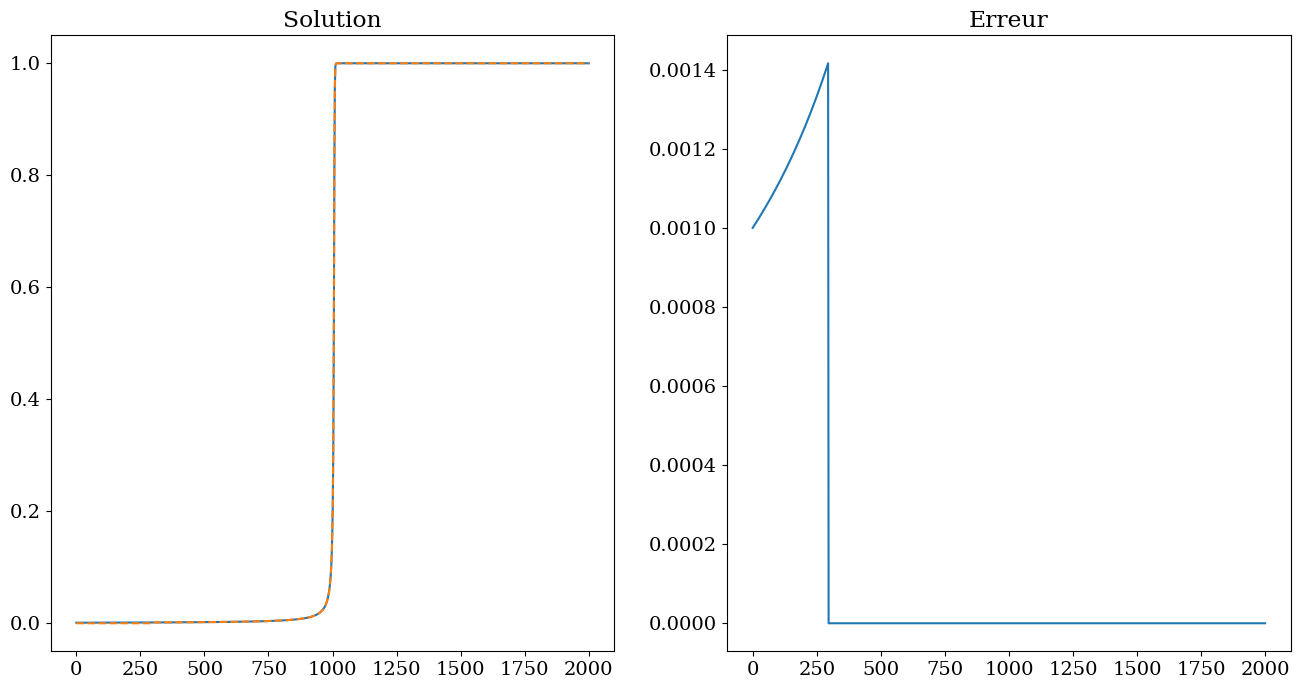
2.5.1.2. cas raide \(\delta=10^{-4}\)#
solution avec un solveur explicite RungeKutta
s = 10**3-1
N = 1000
npas = 0
ncal = 0
def FF(t,U):
global ncal
ncal += 1
return U**2*(1-U)
def solout(t,U):
global npas
npas += 1
return
# parametre
T = np.linspace(0,2*(s+1.),N)
Uex = 1./np.real(1.+lambertw(s*np.exp(s-T)))
# CI
U0 = 1./(s+1.)
# integration RK4
debut = time()
solver = integrate.ode(FF, jac=None).\
set_integrator('dopri5',atol=1.e-8, rtol = 1.e-6, verbosity = True)
# set_integrator('dopri5',verbosity = True)
solver.set_solout(solout)
# CI
t= 0.0
solver.set_initial_value(U0, t)
UU = np.zeros(N)
UU[0] = U0
for i in range(1,N):
if solver.successful():
UU[i]=solver.integrate(T[i])
else:
print("Erreur ODE")
exit
cpu = time() - debut
print("cpu:",cpu)
print("Nbre de pas en temps : ",npas)
print("nombre de calcul de F : ",ncal)
cpu: 0.03062129020690918
Nbre de pas en temps : 2033
nombre de calcul de F : 7204
/tmp/ipykernel_649749/3124434095.py:16: RuntimeWarning: overflow encountered in exp
Uex = 1./np.real(1.+lambertw(s*np.exp(s-T)))
/tmp/ipykernel_649749/3124434095.py:16: RuntimeWarning: overflow encountered in multiply
Uex = 1./np.real(1.+lambertw(s*np.exp(s-T)))
/tmp/ipykernel_649749/3124434095.py:32: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
UU[i]=solver.integrate(T[i])
plt.figure(figsize=(16,8))
plt.subplot(1,2,1)
plt.plot(T,UU)
plt.plot(T,Uex,'--')
plt.title("Solution")
plt.subplot(1,2,2)
plt.plot(T,UU-Uex)
plt.title("Erreur")
Text(0.5, 1.0, 'Erreur')
2.5.1.3. solution avec un solver implicite BDF (lsoda)#
# solver lsoda plus efficace (BDF implicite)
ncal = 0
njac = 0
def FF(t,U):
global ncal
ncal += 1
return U**2*(1-U)
def Jac(t,U):
global njac
njac += 1
return 2*U-3*U*U
debut = time()
solver = integrate.ode(FF, jac=Jac).\
set_integrator('lsoda',atol=1.e-8, rtol = 1.e-6, ixpr=1)
t=0.0
solver.set_initial_value(U0, t)
UU1 = np.zeros(N)
UU1[0]=U0
for i in range(1,N):
if solver.successful():
UU1[i]=solver.integrate(T[i])
else:
print("Erreur ODE")
exit
cpu = time() - debut
print("cpu:",cpu)
print("Nbre de calcul de F:",ncal)
print("Nbre de calcul de J:",njac)
cpu: lsoda-- a switch to the bdf (stiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 166
0.009965658187866211
Nbre de calcul de F: 401
Nbre de calcul de J: 4
in above, r1 = 0.1023165557102D+04 r2 = 0.3159058539115D+01
/tmp/ipykernel_649749/3286385405.py:23: DeprecationWarning: Conversion of an array with ndim > 0 to a scalar is deprecated, and will error in future. Ensure you extract a single element from your array before performing this operation. (Deprecated NumPy 1.25.)
UU1[i]=solver.integrate(T[i])
plt.figure(figsize=(16,8))
plt.subplot(1,2,1)
plt.plot(T,UU,'--')
plt.plot(T,UU1)
plt.title("Solution")
plt.subplot(1,2,2)
plt.plot(T,np.abs(UU-UU1))
plt.title("Erreur")
#plt.xlim(900,1100)
Text(0.5, 1.0, 'Erreur')
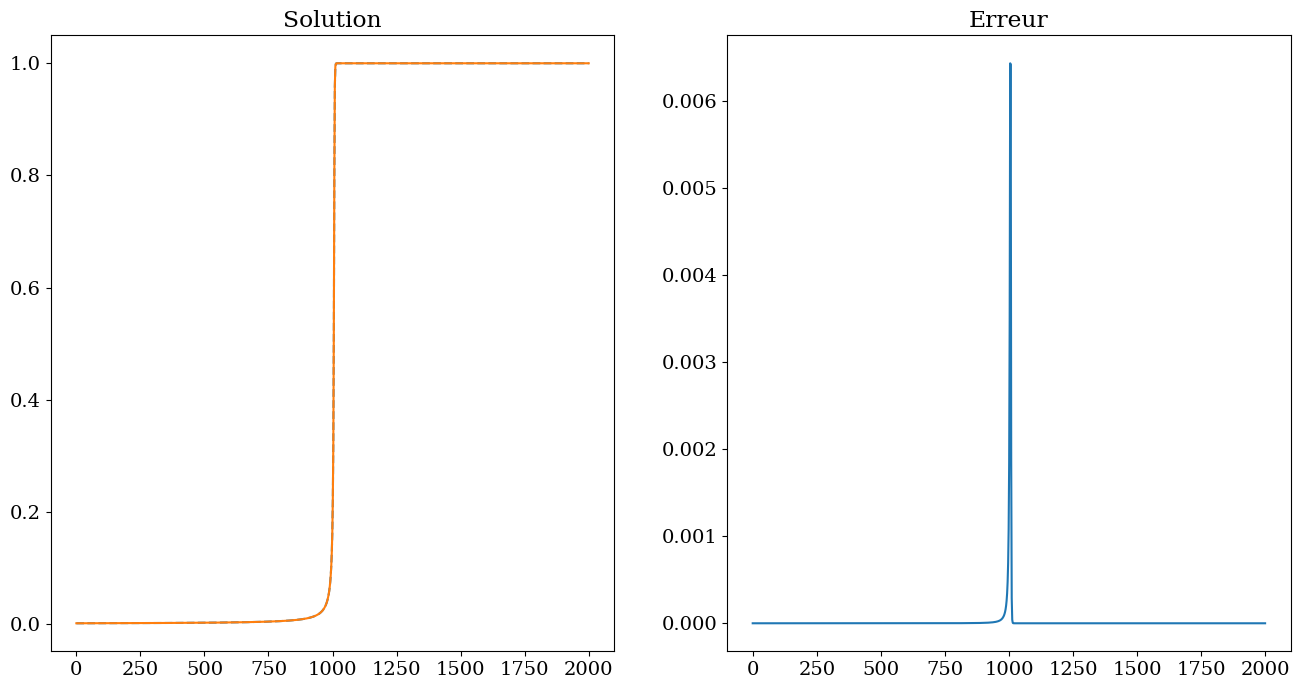
On constate que le solveur implicite permet de résoudre ce problème raide avec un nombre d’itérations et d’évaluations (\(\approx 700\)) de la fonction \(F\) beaucoup plus faible que le solveur explicite RK45 (\(\approx 7000\)), ce qui le rend 4 fois plus efficace (i.e. 4 fois plus rapide en temps cpu).
2.5.2. 2nd exemple: oscillateur de van der pool#
oscillateur non linéaire régit par
pour \(\mu=0\) oscillateur harmonique
pour \(\mu\) petit système non raide
pour \(\mu\) grand système raide
Transformation en un système d’EDO du 1er ordre
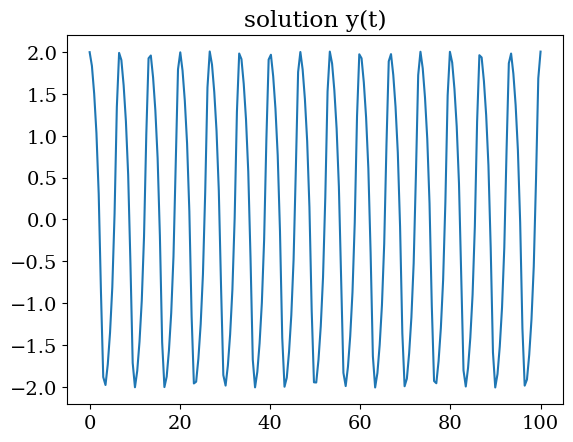
2.5.2.1. cas non raide \(\mu=1\)#
ncal = 0
npas = 0
def F(t,Y,mu):
global ncal
ncal += 1
dY = np.array([Y[1],mu*(1-Y[0]**2)*Y[1]-Y[0]])
return dY
def solout(t,Y):
global npas
npas += 1
return
# cas non raide
mu = 1.0
N = 200
tmax = 100.
debut = time()
solver = integrate.ode(F, jac=None).\
set_integrator('dopri5',atol=1.e-6, rtol = 1.e-3, verbosity = True)
solver.set_solout(solout)
# CI
t = 0.0
U0 = np.array([2. , 0.])
solver.set_initial_value(U0, t).set_f_params(mu)
T = np.linspace(0,tmax,N)
U = np.zeros((N,2))
U[0,:]=U0
for i in range(1,N):
if solver.successful():
U[i] = solver.integrate(T[i])
else:
print("Erreur ODE it=",i)
break
cpu = time() - debut
print("cpu:",cpu)
print("Nbre de calcul de F :",ncal)
print("Nbre de pas en temps:",npas)
plt.plot(T,U[:,0])
plt.title("solution y(t)")
cpu: 0.008172035217285156
Nbre de calcul de F : 2540
Nbre de pas en temps: 583
Text(0.5, 1.0, 'solution y(t)')
2.5.2.2. cas raide \(\mu=1000\)#
solution avec solveur explicite RungeKutta
ne converge pas !!!
2.5.2.2.1. solveur expliciteRK (diverge)#
ncal = 0
npas = 0
def F(t,Y,mu):
global ncal
ncal += 1
dY = np.array([Y[1],mu*(1-Y[0]**2)*Y[1]-Y[0]])
return dY
def solout(t,U):
global npas
npas += 1
return
# cas raide
mu = 1000.0
N = 200
tmax = 3000.
debut = time()
solver = integrate.ode(F, jac=None).\
set_integrator('dopri5',atol=1.e-6, rtol = 1.e-3, verbosity = True)
solver.set_solout(solout)
# CI
t = 0.0
U0 = np.array([2. , 0.])
solver.set_initial_value(U0, t).set_f_params(mu)
T = np.linspace(0,tmax,N)
U = np.zeros((N,2))
U[0,:]=U0
for i in range(1,N):
if solver.successful():
U[i,:] = solver.integrate(T[i])
else:
print("Erreur ODE it=",i)
break
cpu = time() - debut
print("cpu:",cpu)
print("Nbre de calcul de F :",ncal)
print("Nbre de pas en temps:",npas)
plt.plot(T,U[:,0])
plt.title("solution y(t)")
Erreur ODE it= 2
cpu: 0.02121758460998535
Nbre de calcul de F : 3008
Nbre de pas en temps: 500
/home/buffat/venvs/jupyter/lib/python3.10/site-packages/scipy/integrate/_ode.py:438: UserWarning: dopri5: larger nsteps is needed
self._y, self.t = mth(self.f, self.jac or (lambda: None),
Text(0.5, 1.0, 'solution y(t)')
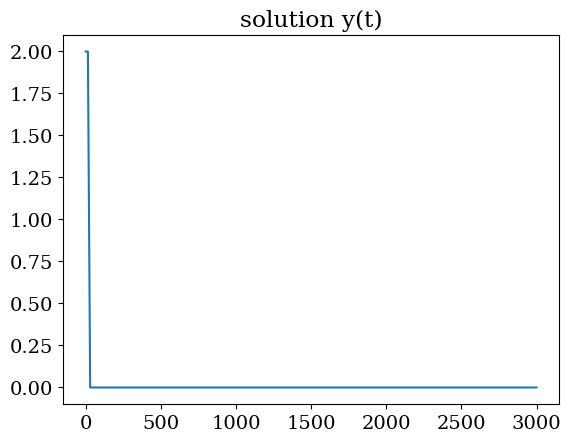
Pour ce cas, le solveur explicite ne converge pas !!!
2.5.2.2.2. solveur implicite BDF (lsoda)#
# solver lsoda plus efficace (BDF implicite)
ncal = 0
njac = 0
mu = 1000.0
def FF(t,Y,mu):
global ncal
ncal += 1
dY = np.array([Y[1] , mu*(1-Y[0]**2)*Y[1]-Y[0]])
return dY
def Jac(t,Y,mu):
global njac
njac += 1
dFdY = np.array([[ 0 , 1.],
[-2*mu*Y[0]*Y[1]-1.,mu*(1-Y[0]**2)]])
return dFdY
N = 100
T = np.linspace(0,tmax,N)
debut = time()
solver = integrate.ode(FF, jac=Jac).\
set_integrator('lsoda',atol=1.e-5, rtol = 1.e-4, ixpr=1)
t = 0.0
U0 = np.array([2. , 0.])
solver.set_f_params(mu)
solver.set_jac_params(mu)
solver.set_initial_value(U0, t)
UU = np.zeros((N,2))
UU[0,:]=U0
for i in range(1,N):
if solver.successful():
UU[i,:] = solver.integrate(T[i])
else:
print("Erreur ODE it=",i)
exit
cpu = time() - debut
print("cpu:",cpu)
print("Nbre de calcul de F:",ncal)
print("Nbre de calcul de J:",njac)
plt.plot(T,UU[:,0])
plt.title("solution y(t)");
lsoda-- a switch to the bdf (stiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 21
in above, r1 = 0.3305202064385D-02 r2 = 0.1916670395710D-02
cpu: 0.006350040435791016
Nbre de calcul de F: 1615
Nbre de calcul de J: 115
lsoda-- a switch to the adams (nonstiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 181
in above, r1 = 0.8048350883061D+03 r2 = 0.2655460477849D-03
lsoda-- a switch to the bdf (stiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 282
in above, r1 = 0.8048500926435D+03 r2 = 0.1137782784124D-02
lsoda-- a switch to the adams (nonstiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 442
in above, r1 = 0.1609557814764D+04 r2 = 0.2645038643414D-03
lsoda-- a switch to the bdf (stiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 537
in above, r1 = 0.1609572906301D+04 r2 = 0.9900625650018D-03
lsoda-- a switch to the adams (nonstiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 697
in above, r1 = 0.2414440458076D+04 r2 = 0.2644669709606D-03
lsoda-- a switch to the bdf (stiff) method has occurred
at t = r1, tentative step size h = r2, step nst = i1
in above message, i1 = 792
in above, r1 = 0.2414455575444D+04 r2 = 0.1007518833444D-02
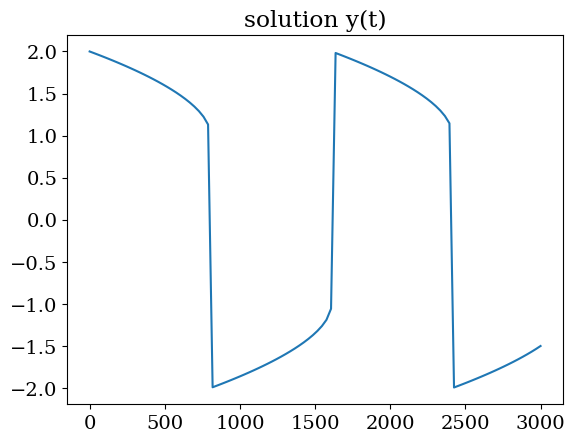
Ce solveur lsoda est très efficace car il sait permuter entre un solveur explicite dans les zones non raides et un solveur implicite dans les zones raides pour obtenir une bonne approximation de la solution
