Traitement de données avec PANDAS

Contenu

2. Traitement de données avec PANDAS#

Marc BUFFAT, Université Claude Bernard Lyon 1

../../_images/python_pandas1.jpg 
%matplotlib inline
from IPython.display import HTML,display
# bibliotheques de base
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14

2.1. BIG DATA#

../../_images/b_1_q_0_p_0.jpg

2.2. croissance du stocage digital#

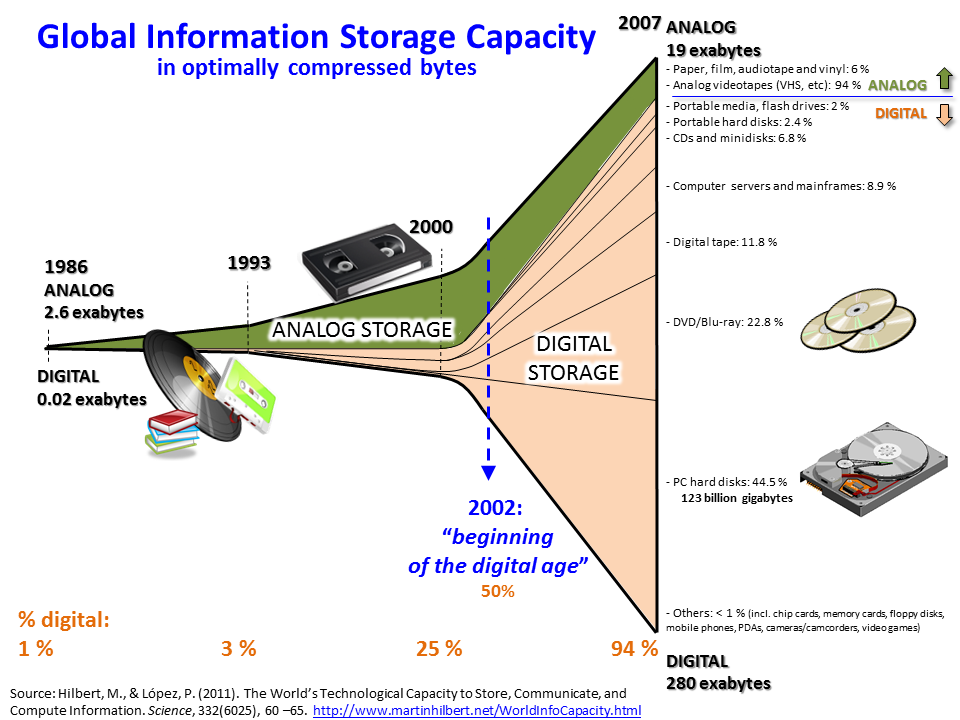
../../_images/Hilbert_InfoGrowth.png

2.3. Les bons outils suivant la taille des données#

  • petits fichiers ( ~ qques ko) : tableur: excel locacl

  • 1 Mo < x < 100 Mo : très lourd avec excel => script: Python (Pandas), R

  • 100 Mo < xx < 100 Go : impossible avec excel ==> script: Python (Pandas), R, SQL

  • 100 Go < xxx < 1 To ===> SQL base de données

  • 1 Tb et + ====> Hadoop

2.4. Traitement des données#

2.4.1. the (old) excel way#

  • utilisation d’un tableur (excel , localc)

  • simple pour des données simples

  • mais tricky pour des traitements complexes (VBA)

2.4.2. the (new) Pandas way#

  • basé sur un vrai language de programmation (Python)

  • traitement complexe des données (cleaning,..)

  • automatisation

  • performance

  • adapté au big data

2.5. Pandas: « Python Library for Data Analysis and Statistics »#

../../_images/python_pandas1.jpg

2.5.1. Pandas: http://pandas.pydata.org#

Pandas (from Panel Data analysis) is a Python package providing fast, flexible, and expressive data structures designed to work with relational or labeled data both. It is a fundamental high-level building block for doing practical, real world data analysis in Python.

pandas is well suited for:

  • Tabular data with heterogeneously-typed columns, as in an SQL table or Excel spreadsheet

  • Ordered and unordered (not necessarily fixed-frequency) time series data.

  • Arbitrary matrix data (homogeneously typed or heterogeneous) with row and column labels

  • Any other form of observational / statistical data sets. The data actually need not be labeled at all to be placed into a pandas data structure

Exemples

2.5.2. Key features:#

  • Easy handling of missing data

  • Size mutability: columns can be inserted and deleted from DataFrame and higher dimensional objects

  • Automatic and explicit data alignment: objects can be explicitly aligned to a set of labels, or the data can be aligned automatically

  • Powerful, flexible group by functionality to perform split-apply-combine operations on data sets

  • Intelligent label-based slicing, fancy indexing, and subsetting of large data sets

  • Intuitive merging and joining data sets

  • Flexible reshaping and pivoting of data sets

  • Hierarchical labeling of axes

  • Robust IO tools for loading data from flat files, Excel files, databases, and HDF5

  • Time series functionality: date range generation and frequency conversion, moving window statistics, moving window linear regressions, date shifting and lagging, etc.

2.6. Data structure in Pandas#

  • Type de données de base: dataframe (tableau de type excel)

Une DataFrame PANDAS est une structure de données tabulaire bidimensionnelle de taille variable, potentiellement hétérogène, avec des axes libellés (lignes et colonnes). est une structure de données bidimensionnelle, c’est-à-dire que les données sont alignées de manière tabulaire en rangées et en colonnes.

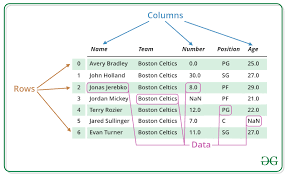
../../_images/dataframe.png 
import pandas as pd

2.7. DataFrame#

  • structure 2D équivalente à un tableur

  • structure hétérogéne avec index (ligne) et column (colonnes)

2.7.1. création à partir de tableaux numpy#

n=5
d = np.ones((n,2))
pd.DataFrame(d)
0 1
0 1.0 1.0
1 1.0 1.0
2 1.0 1.0
3 1.0 1.0
4 1.0 1.0

2.7.2. création à partir de dictionnaire et de tableaux#

2.7.2.1. nom de colonnes#

n = 5
d = { 'One' : np.linspace(1,n,n), 'Two': np.linspace(1,n,n)**2}
pd.DataFrame(d)
One Two
0 1.0 1.0
1 2.0 4.0
2 3.0 9.0
3 4.0 16.0
4 5.0 25.0

2.7.2.2. nom de ligne (index)#

data=pd.DataFrame(d,index=['a','b','c','d','e'])
data
One Two
a 1.0 1.0
b 2.0 4.0
c 3.0 9.0
d 4.0 16.0
e 5.0 25.0

2.7.2.3. selection colonne#

data['Two'] 

a     1.0
b     4.0
c     9.0
d    16.0
e    25.0
Name: Two, dtype: float64

data['Two']['b']

4.0

data['Two'][1]

4.0

2.7.2.4. selection ligne#

data.loc['a']['One']

1.0

data.loc['a']

One    1.0
Two    1.0
Name: a, dtype: float64

data.loc['a']['Two']

1.0

data.loc['a'][0]

1.0

# position ligne/colonne
data.iloc[2,1]

9.0

data.iloc[0,0]

1.0

2.8. DataFrame à partir de fichier csv#

  • fichier csv: Comma-separated values, connu sous le sigle CSV, est un format informatique ouvert représentant des données tabulaires sous forme de valeurs séparées par des virgules dans un fichier texte. C’est un format d’échange courant pour les tableurs.

variante française: chiffre avec virgule, séparateur ;

2.8.1. lecture de données issue de Hubble#

le nom des colonnes est dans le fichier csv et l’index des lignes est numérique (de 0 a n-1)

!head hubble_data.csv

distance,recession_velocity
.032,170
.034,290
.214,-130
.263,-70
.275,-185
.275,-220
.45,200
.5,290
.5,270

data = pd.read_csv("hubble_data.csv")
data.head()
distance recession_velocity
0 0.032 170
1 0.034 290
2 0.214 -130
3 0.263 -70
4 0.275 -185 
data.info()

<class 'pandas.core.frame.DataFrame'>
RangeIndex: 24 entries, 0 to 23
Data columns (total 2 columns):
 #   Column              Non-Null Count  Dtype  
---  ------              --------------  -----  
 0   distance            24 non-null     float64
 1   recession_velocity  24 non-null     int64  
dtypes: float64(1), int64(1)
memory usage: 512.0 bytes

2.8.1.1. change le nom des colonnes#

data.columns = ['dist','rec_vel']
data.tail()
dist rec_vel
19 1.7 960
20 2.0 500
21 2.0 850
22 2.0 800
23 2.0 1090

2.8.1.2. lecture fichier csv sans entete de noms de colonnes#

data = pd.read_csv("hubble_data_no_headers.csv",
                   names=['dist','rec_vel'])
data.tail()

---------------------------------------------------------------------------
FileNotFoundError                         Traceback (most recent call last)
Cell In[19], line 1
----> 1 data = pd.read_csv("hubble_data_no_headers.csv",
      2                    names=['dist','rec_vel'])
      3 data.tail()

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/util/_decorators.py:211, in deprecate_kwarg.<locals>._deprecate_kwarg.<locals>.wrapper(*args, **kwargs)
    209     else:
    210         kwargs[new_arg_name] = new_arg_value
--> 211 return func(*args, **kwargs)

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/util/_decorators.py:331, in deprecate_nonkeyword_arguments.<locals>.decorate.<locals>.wrapper(*args, **kwargs)
    325 if len(args) > num_allow_args:
    326     warnings.warn(
    327         msg.format(arguments=_format_argument_list(allow_args)),
    328         FutureWarning,
    329         stacklevel=find_stack_level(),
    330     )
--> 331 return func(*args, **kwargs)

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:950, in read_csv(filepath_or_buffer, sep, delimiter, header, names, index_col, usecols, squeeze, prefix, mangle_dupe_cols, dtype, engine, converters, true_values, false_values, skipinitialspace, skiprows, skipfooter, nrows, na_values, keep_default_na, na_filter, verbose, skip_blank_lines, parse_dates, infer_datetime_format, keep_date_col, date_parser, dayfirst, cache_dates, iterator, chunksize, compression, thousands, decimal, lineterminator, quotechar, quoting, doublequote, escapechar, comment, encoding, encoding_errors, dialect, error_bad_lines, warn_bad_lines, on_bad_lines, delim_whitespace, low_memory, memory_map, float_precision, storage_options)
    935 kwds_defaults = _refine_defaults_read(
    936     dialect,
    937     delimiter,
   (...)
    946     defaults={"delimiter": ","},
    947 )
    948 kwds.update(kwds_defaults)
--> 950 return _read(filepath_or_buffer, kwds)

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:605, in _read(filepath_or_buffer, kwds)
    602 _validate_names(kwds.get("names", None))
    604 # Create the parser.
--> 605 parser = TextFileReader(filepath_or_buffer, **kwds)
    607 if chunksize or iterator:
    608     return parser

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:1442, in TextFileReader.__init__(self, f, engine, **kwds)
   1439     self.options["has_index_names"] = kwds["has_index_names"]
   1441 self.handles: IOHandles | None = None
-> 1442 self._engine = self._make_engine(f, self.engine)

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/parsers/readers.py:1735, in TextFileReader._make_engine(self, f, engine)
   1733     if "b" not in mode:
   1734         mode += "b"
-> 1735 self.handles = get_handle(
   1736     f,
   1737     mode,
   1738     encoding=self.options.get("encoding", None),
   1739     compression=self.options.get("compression", None),
   1740     memory_map=self.options.get("memory_map", False),
   1741     is_text=is_text,
   1742     errors=self.options.get("encoding_errors", "strict"),
   1743     storage_options=self.options.get("storage_options", None),
   1744 )
   1745 assert self.handles is not None
   1746 f = self.handles.handle

File ~/venvs/jupyter/lib/python3.10/site-packages/pandas/io/common.py:856, in get_handle(path_or_buf, mode, encoding, compression, memory_map, is_text, errors, storage_options)
    851 elif isinstance(handle, str):
    852     # Check whether the filename is to be opened in binary mode.
    853     # Binary mode does not support 'encoding' and 'newline'.
    854     if ioargs.encoding and "b" not in ioargs.mode:
    855         # Encoding
--> 856         handle = open(
    857             handle,
    858             ioargs.mode,
    859             encoding=ioargs.encoding,
    860             errors=errors,
    861             newline="",
    862         )
    863     else:
    864         # Binary mode
    865         handle = open(handle, ioargs.mode)

FileNotFoundError: [Errno 2] No such file or directory: 'hubble_data_no_headers.csv'

2.8.2. accés aux données#

data.info()

2.8.2.1. selection colonne#

data['dist'].tail()

2.8.2.2. sélection de ligne dans la colonne#

data['dist'][0:5]

2.8.2.3. sélection de plusieurs colonnes#

data[['rec_vel','dist','rec_vel']].head()

2.8.3. calcul sur les données#

2.8.3.1. calcul de l’énergie: \(E = K*dist + 0.5 *v^2\)#

K = 1000.
data['E'] = K*data['dist'] + 0.5*data['rec_vel']**2
data['dist2'] = data['dist']**2
data.head()

2.8.3.2. suppression d’une colonne#

del data['dist2']
data.head()

2.8.3.3. suppression d’un ligne (attention paramêtre inplace)#

data.drop(1)

data.head()

data.iloc[1,0]

data.drop(1,inplace=True)
data.head()

2.8.4. indexation des données:#

Au lieu d’utiliser l’indexation numérique de 0 à n-1, on va indexer les données par rapport à une colonne, par ex. la colonne “dist” pour annalyser

  • vel = F(dist)

  • E = G(dist)

data.set_index("dist",inplace=True)
data.head()

2.8.4.1. tracer des données rec_vel = F(dist)#

data['rec_vel'].plot(figsize=(12,6),lw=2,grid=True,style='-o')
plt.title("")

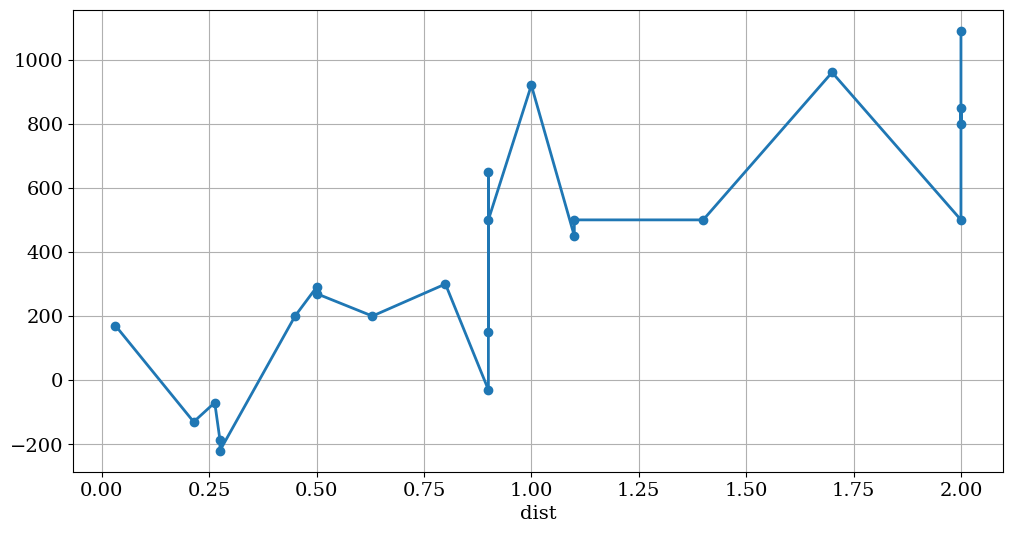
data['E'].plot(figsize=(12,6),lw=2,grid=True,style='-o')

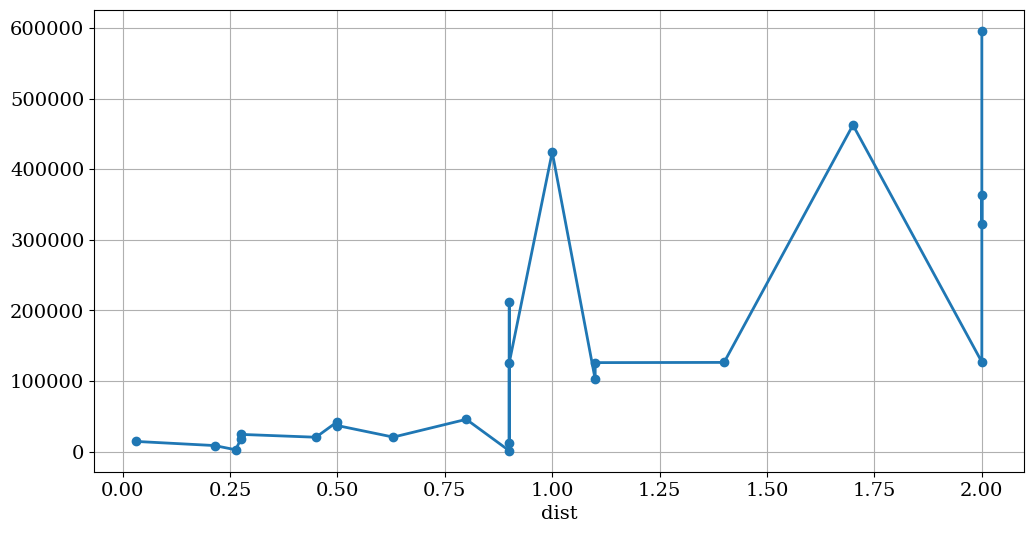
2.8.4.2. traitement statistique:#

moyenne , medianne …

  • analyse par colonne

energy = data['E']
type(energy)

energy.mean(), energy.median()

  • analyse globale

data.describe()

2.8.5. analyse statistique#

  • variance, covariance, moyenne …..

matrice de covariance entre 3 tableaux x,y,z

\[\begin{split} cov_{x,y,z} = \left[ \begin{array}{ccc} cov_{x,x} & cov_{x,y} & cov_{x,z} \\ cov_{y,x} & cov_{y,y} & cov_{y,z} \\ cov_{z,x} & cov_{z,y} & cov_{z,z} \end{array} \right] = \left[ \begin{array}{ccc} \sigma^2_{x} & \sigma_{xy} & \sigma_{xz} \\ \sigma_{yx} & \sigma^2_{y} & \sigma_{yz} \\ \sigma_{zx} & \sigma_{zy} & \sigma^2_{z} \end{array} \right] \end{split}\]

avec (\(E\) est l’opérateur moyenne \(E(X) = \bar{X}\)) $\( cov_{x,y} = E[(X – E[X])(Y – E[Y])] = \overline{(X-\bar{X})(Y-\bar{Y})} = \frac{\sum(X_i – \bar{X})(Y_i – \bar{Y})}{N} \)$

data1 = data.reset_index()
data1.head()

CV = data1.cov()
display(CV)

# CV est un datafrme : accès
CV['rec_vel']['dist'] , CV.iloc[0,1]

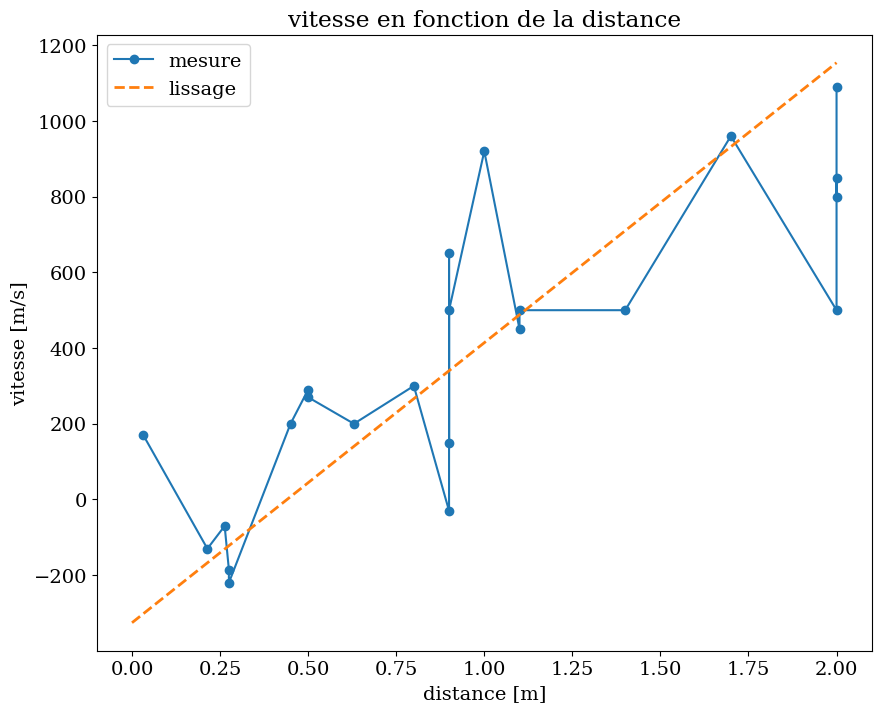
vérification: lissage par droite moindre carré V=F(dist)

\[ V = a*dist + b \]

avec \( a = \frac{\sigma_{V,V}}{\sigma_{V,dist}} \) et \( b = \bar{V} - a * \overline{dist} \)

# verification lissage par droite moindre carré V=F(dist)
a = CV.iloc[1,1]/CV.iloc[1,0]
b = data1['rec_vel'].mean() - a * data1['dist'].mean()
print(a,b)

rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
X = np.linspace(0.,2.,21)
plt.figure(figsize=(10,8))
plt.plot(data1['dist'],data1['rec_vel'],'-o',label="mesure")
plt.plot(X,a*X+b,'--',lw=2,label="lissage")
plt.legend()
plt.xlabel('distance [m]')
plt.ylabel('vitesse [m/s]')
plt.title("vitesse en fonction de la distance")

2.8.6. modification des données (loc, iloc)#

attention à l’aliasing !!! de nombreuses fonctions renvoient une copy du tableau (paramêtre inplace)

data['E']

data['E'][2.]=1620
print(data.tail())

2.8.6.1. utilisation de .at (attention ligne, colonne)#

data.at[2.,'E']=1800
print(data.tail())

data.loc[2,'E']

2.8.7. autres structures de données#

  • Serie 1D

  • xarray: multi-dimensionnal

voir http://pandas.pydata.org

2.9. DataFrame a partir de fichier csv (exemple 2)#

data = pd.read_csv("wages_hours.csv")
data.head()

2.9.1. selection du bon séparateur#

data = pd.read_csv("wages_hours.csv", sep = "\t")
data.head()

#pd.read_csv?

2.9.2. Extraction de colonnes a traiter#

data2 = data[["AGE", "RATE"]]
data2.head()

2.9.3. tri des données#

data_sorted = data2.sort_values("AGE")
data_sorted.head()

2.9.3.1. indexation en fonction de la colonne AGE#

data_sorted.set_index("AGE", inplace=True)
data_sorted.head()

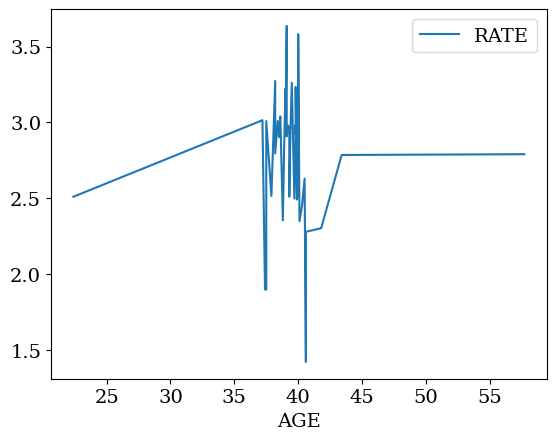
2.9.3.2. tracer du salaire en fonction de l’age#

data_sorted.plot()
plt.show()

2.10. données fonction du temps#

2.10.1. gestion date (conversion)#

date=pd.to_datetime('2016-09-29T23:00:00+02:00')
date

2.10.2. localisation: timezone#

  • heure universelle

  • timezone: Europe/Paris

date.tz_convert(tz='Europe/Paris')

2.10.3. serie temporelle (regroupement)#

  • création de la série temporelle puis du dataframe

date=pd.date_range('2015-01', '2015-12-31',
                   freq='D')
date

ts = pd.Series(np.random.randn(len(date)), 
               index=date)
data= ts.to_frame(name='val')
data.head()

2.10.4. aggregation / mois#

data['Mois']=data.index.month
data.head()

datam=data.groupby('Mois').aggregate(np.mean)
datam.head()

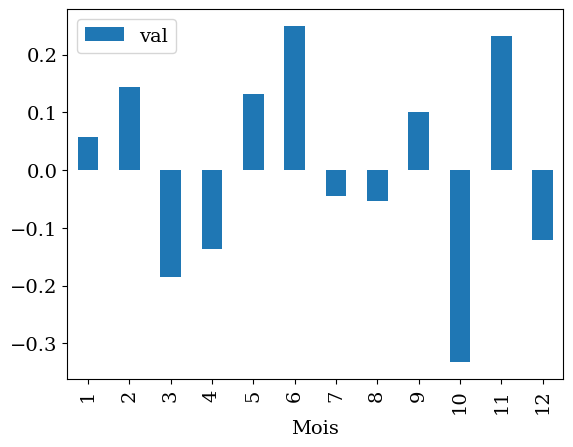
datam.plot(kind='bar')

2.10.5. boucle sur les valeurs d’une colonne#

somme=0.0
for val in data['val']:
    somme += val
print("somme de la colonne :",somme)

2.10.6. avec un index#

data['val2']=0.0
for index,row in data.iterrows():
    val = row['val']
    data.loc[index,'val2'] = val**2
data.head()

2.11. Bibliothèque spécialisée#

Visualisation de données (statistique)

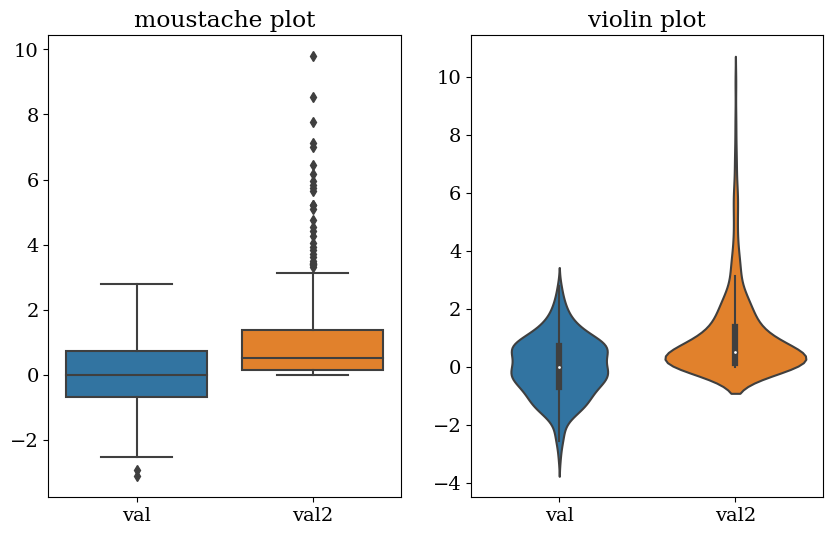
  • Boîte à moustaches: représentation visuelle permettant mesurer la distribution des données.

    • Le minimum est affiché à l’extrême gauche du graphique, à la fin de la « moustache » de gauche

    • Le premier quartile, Q1, est l’extrême gauche de la boîte (moustache gauche)

    • La médiane est représentée par une ligne au centre de la boîte

    • Troisième quartile, Q3, affiché à l’extrême droite de la boîte (moustache droite)

    • Le maximum est à l’extrême droite de la case

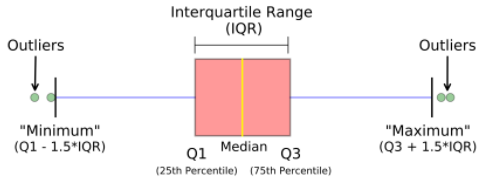
../../_images/moustache.png

  • On appelle Écart interquartile ou InterQuartile Range: IQR = Q3-Q1 qui mesure la dispersion des données (estimateur statistique robuste)

  • Minimum = Q1 - 1.5 IQR

  • Maximum = Q3 + 1.5 IQR

  • les points en dehors d’une répartition standard (outliers), i.e en dehors du [minimum:maximum], sont marquées comme des points

violin plot (variante)

  • Un violin plot est utilisé pour visualiser la distribution des données et sa densité de probabilité.

seaborn: statistical data visualization

import seaborn as sns

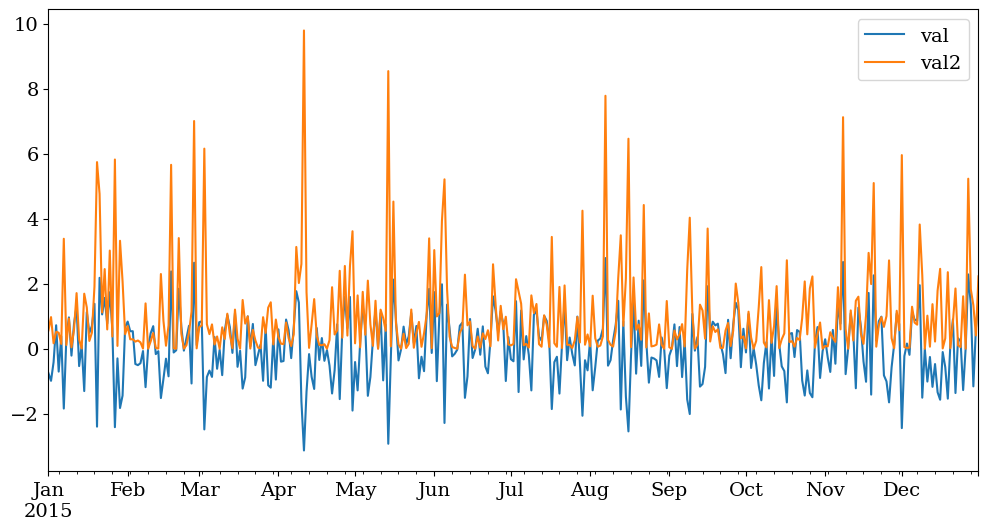
# donnees brutes
plt.figure(figsize=(12,6))
data['val'].plot(label='val')
data['val2'].plot(label='val2')
plt.legend()

plt.figure(figsize=(10,6))
plt.subplot(1,2,1)
sns.boxplot(data=data[['val','val2']])
plt.title("moustache plot");
plt.subplot(1,2,2)
sns.violinplot(data=data[['val','val2']])
plt.title("violin plot");

2.12. Bibliographie#

apprendre à lire et à chercher dans la documentation (très (trop) riche !!)

2.13. FIN#

Contenu