1. Traitement de données#
Marc BUFFAT , Université Claude Bernard Lyon 1
1.1. Traitement de données#
Les différentes phases
importation des données (lecture)
pré-traitement
analyse des données
exportation des données (tracé, écriture)
1.1.1. Format des données#
organisation des données dans les fichiers
format standard : csv, xml, json
Comma-Separated Values est un format texte ouvert représentant des données tabulaires sous forme de valeurs séparées par des virgules.
EXtensible Markup Language est un métalangage informatique de balisage générique pour décrire un document structuré
JavaScript Object Notation (JSON) est un format de données textuelles dérivé de la notation des objets du langage JavaScript
utilisation de librairies
format spécifique:
création d’une librarie
1.2. Fichier informatique#
définition (Wikipédia) un fichier informatique est une collection d’informations numériques (séquences d’octets) réunies sous un même nom, enregistrées sur un support de stockage tel qu’un disque dur, un CD-ROM, une clé USB …
En vue de faciliter leur organisation, les fichiers sont disposés dans des systèmes de fichiers qui permettent de placer les fichiers dans des emplacements appelés répertoires ou dossiers eux-mêmes organisés selon le même principe de manière à former une hiérarchie arborescente
Sur le système de l’ordinateur, un fichier est repéré par son nom avec éventuellement une extension et le répertoire dans lequel il se trouve.
En calcul scientifique, on considère 2 types principaux de fichiers:
des fichiers de programmes qui contiennent un code informatique exécutable par l’ordinateur, sous 2 formes principales:
fichiers exécutables qui contiennent un code binaire directement exécutable par le processeur (extension .exe sous windows). Ces programmes ne sont pas modifiables et sont propre à l’ordinateur utilisé (programmes commerciaux ou propriétaires)
fichiers sources qui contiennent le code source du programme dans un langage de programmation (extension .py pour les programmes Python). Ces programmes peuvent être modifiés et être exécuter sur n’importe quel ordinateur.
des fichiers de données qui contiennent des données (data) crées et manipulées par les programmes, sous 2 formes principales:
des fichiers binaires qui contiennent l’information brute, utilisant le codage de l’ordinateur (le plus efficace pour le stockage)
des fichiers textes qui contiennent les données écrites sous forme de lignes de texte (format le plus simple à manipuler)
Dans la suite on ne considérera que les fichiers programmes Python (extension .py) et des fichiers de données textes (extension .dat).
Pour éviter des problèmes de compatibilités entre systèmes informatiques, on choisira des noms de fichiers sans caractères accentués, sans espace ni caractéres spéciaux (autre que . ou _ ou - )
1.3. Fichier de programme (ou script) sous Python#
un fichier contenant un programme Python a par convention une extension .py. Un simple éditeur de texte (notepad sous Windows) suffit pour créer et modifier un programme Python
gedit « voir le site gedit » un éditeur simple et efficace
vim et variante « soir le site vim » un éditeur de référence pour les programmeurs
1.3.1. Exemple: trace de courbes de Lissajous#
Une courbe de Lissajous (d’après le physicien français « Jules Antoine Lissajous ») est une courbe paramétrique du plan dont les composantes sont des fonctions périodiques du paramètre (en générale le temps en physique, et que l’on peut observer avec un oscilloscope).
Le programme Python suivant lissajous.py trace les courbes de Lissajous suivantes
Le rapport \(n=\frac{p}{q}\) est le paramètre de la courbe et \(\phi\) le déphassage. Le temps \(T\) de parcours de la courbe est le plus petit commun multiple de \(p\) et \(q\): $\(T=pcm(p,q)=\frac{pq}{pgcd(p,q)}\)$
1.3.1.1. programme python#
%%bash --err /dev/null
ls -al lissajous.py
cat lissajous.py
-rwxrwxr-x 1 buffat buffat 1598 août 24 2022 lissajous.py
#! /usr/bin/env python
# -*- coding: utf-8 -*-
"""
tracer de courbe de Lissajous
d'après https://sites.google.com/site/sdcoding/python/physics-with-python
@author: marc buffat
"""
import numpy as np
import matplotlib.pyplot as plt
def pgcd(a, b):
"""calcul du pgcd de a et b par l'algorithme d'Euclide."""
while b:
a, b = b, a % b
return a
def Lissajous(p,q,phi,N):
""" calcul de N points d'une courbe de Lissajous"""
omega1 = 2*np.pi/p
omega2 = 2*np.pi/q
# temps d'étude = lcm(p,q)
T = p*q/pgcd(p,q)
t = np.linspace(0., T, N)
# equations parametriques
x = np.sin(omega1*t)
y = np.sin(omega2*t+phi)
return t,x,y
def LissajousFigure(p,q,phi):
""" trace de courbe de lissajous
p,q : parametres entiers des courbes x(t),y(t)
phi: déphasage
"""
# pulsation des 2 courbes
om1 = 2*np.pi/p
om2 = 2*np.pi/q
# temps d'étude
#T = lcm(p,q)
T = p*q/pgcd(p,q)
t = np.arange(0., T, T/1000.0)
# equations parametriques
x = np.sin(om1*t)
y = np.sin(om2*t+phi)
# tracer
plt.plot(x, y, linewidth=2)
plt.title("p=%d q=%d"%(p,q))
plt.xlabel("x(t)")
plt.ylabel("y(t)")
plt.axis([-1.,1.,-1.,1.])
plt.axis('equal')
return
# programme principal du module
if __name__ == "__main__":
# tracer de 3 courbes de Lissajous
plt.figure(figsize=(12,6))
plt.subplot(131)
LissajousFigure(1,2,np.pi/2)
plt.subplot(132)
LissajousFigure(3,2,np.pi/2)
plt.subplot(133)
LissajousFigure(5,4,np.pi/2)
plt.savefig('lissajous.png')
1.3.1.2. execution#
%matplotlib inline
from __future__ import print_function
# bibliotheques de base
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
#from jupyterthemes import jtplot
#jtplot.style()
#jtplot.style(context='talk',fscale=1.4,spines=True,ticks=True,grid=False,figsize=(12,6))
print("Initialisation OK")
Initialisation OK
%%bash
echo "execution avec interpreteur python"
python3 lissajous.py
ls -al lissajous.png
execution avec interpreteur python
-rw-rw-r-- 1 buffat buffat 97883 mars 19 18:06 lissajous.png
1.3.2. Notebook ipython#
format json (code + texte + sortie ..)
Lissajous.ipynb
%%bash
head -20 Lissajous.ipynb
{
"cells": [
{
"cell_type": "code",
"execution_count": null,
"metadata": {},
"outputs": [],
"source": [
"import numpy as np\n",
"import matplotlib.pyplot as plt\n",
"\n",
"def pgcd(a, b):\n",
" \"\"\"calcul du pgcd de a et b par l'algorithme d'Euclide.\"\"\"\n",
" while b:\n",
" a, b = b, a % b\n",
" return a\n",
"\n",
"def lcm(a, b):\n",
" \"\"\"calcul du plus petit commun multiple.\"\"\"\n",
" return a * b // pgcd(a, b)\n",
1.4. module (ou librairie)#
module fichier contenant des fonctions et des définitions en python (bibliothèque)
nom du module nom du fichier sans l’extension .py
utilisation du module mon_module.py
import mon_module
import mon_module as mn
from mom_module import ma_fonction
from mon_module import *
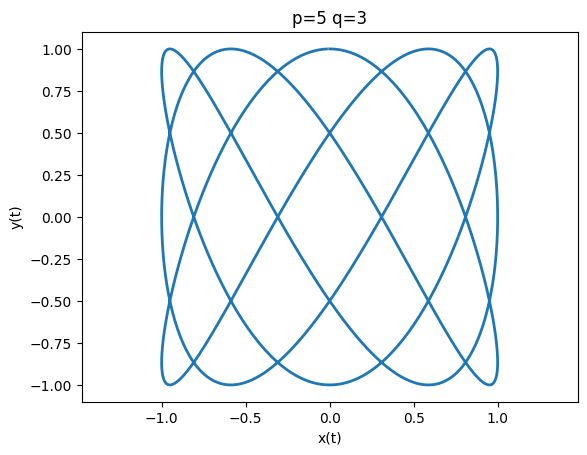
from lissajous import pgcd,LissajousFigure
print(pgcd(21,9))
LissajousFigure(5,3,np.pi/2)
3
1.5. Fichiers de données sous Python#
Comme dans la pluspart des langages informatiques, lire ou écrire dans un fichier, on va associer à un fichier (à son nom) une variable informatique de type file, qui posséde des fonctions (ou méthodes) permettant de lire ou écrire des données dans le fichier.
1.5.1. fonction de lecture/écriture#
ouverture d’un fichier mon_fichier.dat en lecture: f=open(« nom_fichier.dat »,”r”)
ou en écriture: f=open(« nom_fichier.dat »,”w”)
lecture / ecriture (caractères) f.read(n) ou f.readline() f.write(chaine)
lecture / écriture de tableaux (numpy) A=loadtxt(file (ou nom de fichier)) savetxt(file (ou nom de fichier), A)
fermeture du fichier f.close()
1.6. Exemple traitement de fichiers#
Une courbe de Lissajous (d’après le physicien français « Jules Antoine Lissajous ») est une courbe paramétrique du plan dont les composantes sont des fonctions périodiques du paramètre (en générale le temps en physique, et que l’on peut observer avec un oscilloscope).
L’expression d’une courbe de Lissajous est la suivante
Le rapport \(n=\frac{p}{q}\) est le paramètre de la courbe et \(\phi\) le déphassage. Le temps \(T\) de parcours de la courbe est le plus petit commun multiple de \(p\) et \(q\): $\(T=pcm(p,q)=\frac{pq}{pgcd(p,q)}\)$
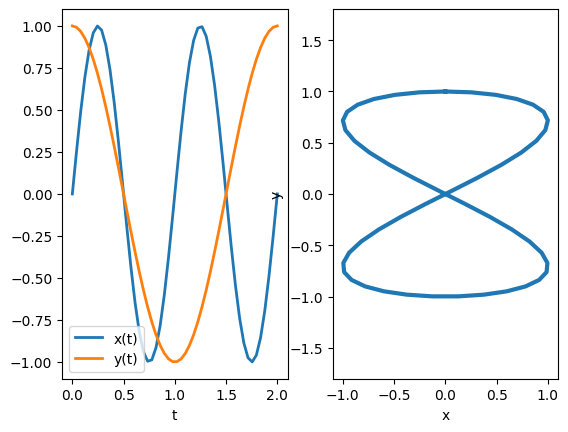
from lissajous import Lissajous
# calcul des points
p=1; q=2;
N=50
t,x,y=Lissajous(p,q,np.pi/2,N)
plt.subplot(1,2,1)
plt.plot(t,x,label='x(t)',lw=2)
plt.plot(t,y,label='y(t)',lw=2)
plt.xlabel('t')
plt.legend()
plt.subplot(1,2,2)
plt.plot(x,y,lw=3)
plt.axis('equal')
plt.xlabel('x')
plt.ylabel('y')
Text(0, 0.5, 'y')
1.6.1. format d’écriture#
écriture sur fichiers de \(n\) points d’une courbe de Lissajous avec le format suivant
# ligne de commentaire
t0 x0 y0
.......
ti xi yi
.......
tn-1 xn-1 yn-1
1.7. Génération des données#
import numpy as np
import matplotlib.pyplot as plt
from lissajous import Lissajous
# calcul des points
p=1; q=2;
N=50
t,x,y=Lissajous(p,q,np.pi/2,N)
1.7.1. Écriture ligne / ligne (la plus générale)#
print("tableau:",t.shape,type(t))
F=open("lissajous.dat","w")
F.write("# courbe de lissajous avec p={} q={}\n".format(p,q))
for i in range(N):
F.write("{:.8g} {:.8g} {:.8g}\n".format(t[i],x[i],y[i]))
F.close()
tableau: (50,) <class 'numpy.ndarray'>
%%bash --err /dev/null
ls -al lissajous.dat
head lissajous.dat
-rw-rw-r-- 1 buffat buffat 1650 mars 19 18:06 lissajous.dat
# courbe de lissajous avec p=1 q=2
0 0 1
0.040816327 0.25365458 0.99179001
0.081632653 0.49071755 0.96729486
0.12244898 0.69568255 0.92691676
0.16326531 0.85514276 0.8713187
0.20408163 0.95866785 0.80141362
0.24489796 0.99948622 0.71834935
0.28571429 0.97492791 0.6234898
0.32653061 0.88659931 0.51839257
1.7.2. Écriture sous forme d’un tableau#
F=open("lissajous.dat","w")
entete=" courbe de lissajous avec p={} q={}".format(p,q)
np.savetxt(F,np.transpose([t,x,y]),header=entete)
F.close()
%%bash --err /dev/null
ls -al lissajous.dat
head lissajous.dat
-rw-rw-r-- 1 buffat buffat 3835 mars 19 18:06 lissajous.dat
# courbe de lissajous avec p=1 q=2
0.000000000000000000e+00 0.000000000000000000e+00 1.000000000000000000e+00
4.081632653061224164e-02 2.536545839095073474e-01 9.917900138232461638e-01
8.163265306122448328e-02 4.907175520039378513e-01 9.672948630390294511e-01
1.224489795918367319e-01 6.956825506034863826e-01 9.269167573460217469e-01
1.632653061224489666e-01 8.551427630053460849e-01 8.713187041233895203e-01
2.040816326530612013e-01 9.586678530366605777e-01 8.014136218679566159e-01
2.448979591836734637e-01 9.994862162006878936e-01 7.183493500977276014e-01
2.857142857142856984e-01 9.749279121818236193e-01 6.234898018587335944e-01
3.265306122448979331e-01 8.865993063730001067e-01 5.183925683105251592e-01
1.7.3. Lecture des données#
1.7.3.1. lecture ligne / ligne#
print("Lecture du fichier ligne/ligne")
F=open("lissajous.dat","r")
line=F.readline()
print(line)
lines=F.readlines()
F.close()
N = len(lines)
print("nbre de valeurs ",N)
t = np.zeros(N); x = np.zeros(N); y = np.zeros(N)
i = 0
for line in lines:
mots = line.split()
t[i] = float(mots[0])
x[i] = float(mots[1])
y[i] = float(mots[2])
i = i+1
plt.plot(x,y,'-o')
plt.axis('equal')
Lecture du fichier ligne/ligne
# courbe de lissajous avec p=1 q=2
nbre de valeurs 50
(-1.0994348378207568,
1.0994348378207568,
-1.0978426623878532,
1.0998972696375169)
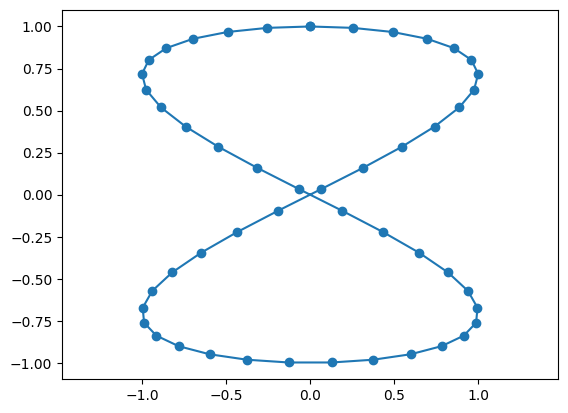
1.7.3.2. lecture sous forme de tableau#
print("lecture du fichier avec loadtxt (tableau)")
A=np.loadtxt("lissajous.dat")
print("lecture des données taille=",A.shape)
t=A[:,0]
x=A[:,1]
y=A[:,2]
# tracer
plt.plot(x,y,'-o',lw=2)
plt.axis('equal')
lecture du fichier avec loadtxt (tableau)
lecture des données taille= (50, 3)
(-1.0994348378207568,
1.0994348378207568,
-1.0978426623878532,
1.0998972696375169)
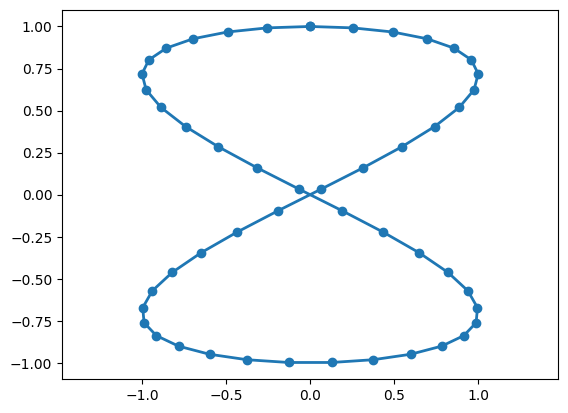
1.8. Pré-traitement des données#
1.8.1. trie des données:#
algorithme trie bulle (bubble sort) L’algorithme parcourt le tableau et compare les éléments consécutifs. Lorsque deux éléments consécutifs ne sont pas dans l’ordre, ils sont échangés.
Après un premier parcours complet du tableau, le plus grand élément est forcément en fin de tableau, à sa position définitive. On applique donc l’algorithme recursivement au reste du tableau.
pseudo-code
algorithme tri_bulles(Tableau T)
pour i allant de taille de T - 1 à 1
pour j allant de 0 à i - 1
si T[j+1] < T[j]
échanger(T[j+1],T[j])
# l'algorithme modifie le tableau T
retour
# algorithme de trie bulles
def tri_bulles(T):
for i in range(T.size-1,0,-1):
for j in range(i):
if T[j+1]<T[j]:
val=T[j+1]
T[j+1] = T[j]
T[j] = val
return
X=np.random.rand(5)
print("X original:",X)
tri_bulles(X)
print("X trie :",X)
X original: [0.11878488 0.63804203 0.69299384 0.73617064 0.62993621]
X trie : [0.11878488 0.62993621 0.63804203 0.69299384 0.73617064]
1.8.2. analyse par FFT d’un signal périodique#
Soit un signal \({a_k}\) de \(n\) valeurs échantillonné à des temps \(t_k\)
la FFT de \(\{a_k\}_{k=0,n-1}\) est un tableau de \(n\) complexes \(\{A_k\}_{k=0,n-1}\) t.q: $\( A_k = \sum_{m=0}^{N-1} a_m e^{- 2\pi \imath \frac{mk}{n}} \)\( \)A[1:n/2]\( correspond aux termes de fréquence positive et \)A[n/2:n]\( aux termes de fréquence négative. Si \)a\( est un tableau réel, alors ces termes sont complexes conjugués. Par convention les amplitudes ne sont pas normalisées et sont donc multipliées par \)n$.
ATTENTION au dernier point !!! pour une période \(T\), un signal est echantilloné sur \(n\) points aux temps \(t=0,t=dt, t=(n-a)dt\) avec \(dt=T/n\)
1.8.2.1. exemple: signal harmonique#
phi = np.pi/4
n = 8
t = np.linspace(0,4.,n,endpoint=False)
x = 3*np.cos(np.pi*t+phi)
print("Signal :",x)
# FFT
xf = np.fft.fft(x)
print("FFT xf:",xf)
# norme
xs = np.abs(xf)/n
print(xs)
Signal : [ 2.12132034 -2.12132034 -2.12132034 2.12132034 2.12132034 -2.12132034
-2.12132034 2.12132034]
FFT xf: [ 1.77635684e-15+0.00000000e+00j -3.14018492e-15+1.33226763e-15j
8.48528137e+00+8.48528137e+00j 3.14018492e-15-1.33226763e-15j
1.77635684e-15+0.00000000e+00j 3.14018492e-15+1.33226763e-15j
8.48528137e+00-8.48528137e+00j -3.14018492e-15-1.33226763e-15j]
[2.22044605e-16 4.26389243e-16 1.50000000e+00 4.26389243e-16
2.22044605e-16 4.26389243e-16 1.50000000e+00 4.26389243e-16]
t1 = np.linspace(0,4.,100)
x1 = 3*np.cos(np.pi*t1+phi)
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(t1,x1)
plt.plot(t,x,'o')
plt.ylim([-4.,4])
plt.title('signal')
plt.subplot(1,2,2)
plt.plot(xs,'-o')
plt.title('norme FFT')
Text(0.5, 1.0, 'norme FFT')
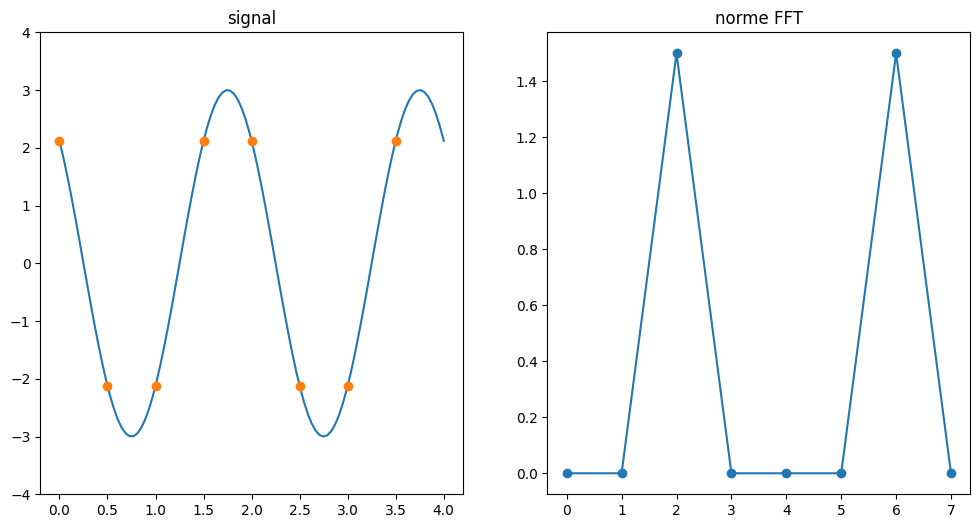
Pour un signal périodique sur \(T\), la FFT sur n points décompose le signal en \(n/2 - 1\) harmoniques de période \([T, T/2, ... ]\) et un mode continu.
Les \(n/2\) fréquences associées sont donc \([0, 1/T,2/T,..]\) avec \(T=n dt\) (où \(dt\) est le pas d’échantillonage)
Normalisation de l’amplitude (\(* 2/n\))
# normalisation
xs = (2./n) * np.abs(xf[0:n//2])
# frequence
dt = t[1]-t[0]
fs = np.linspace(0,n//2,n//2,endpoint=False)/(n*dt)
print(xs,fs)
print("frequence fs",fs)
plt.semilogy(fs,xs,'o')
plt.title("spectre de puissance")
[4.44089210e-16 8.52778486e-16 3.00000000e+00 8.52778486e-16] [0. 0.25 0.5 0.75]
frequence fs [0. 0.25 0.5 0.75]
Text(0.5, 1.0, 'spectre de puissance')
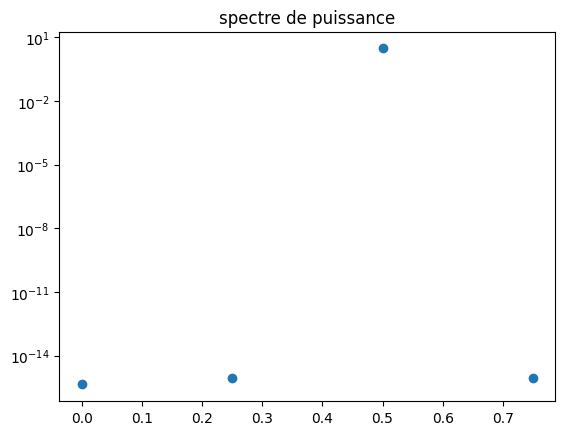
print("Amplitude :",xs[2])
print("Fréquence :",fs[2])
print("phase :",np.angle(xf[2]))
Amplitude : 2.9999999999999987
Fréquence : 0.5
phase : 0.785398163397448
1.9. TP traitement de données#
On veut traiter des données stockées dans un fichier contenant la valeur de 2 quantités X et Y périodique en fonction du temps t sur une période T.
Ces valeurs sont stockées par colonne suivant la structure ci dessous:
# titre
t0 x0 y0
t1 x1 y1
.......
La valeur de t dans ce fichier n’est pas forcement triée et les données X,Y sont bruitées.
L’objectif de cette étude est d’analyser ces données \(X_i,Y_i\) en fonction du temps t et d’en déduire leurs pulsations, puis les paramêtres de Lissajous p et q.
# generation des données
from lissajous import Lissajous
uid=1234
np.random.seed(uid)
p = np.random.randint(1,10)
q = np.random.randint(1,10)
print("parametres ",p,q)
N = 512
# calcul sur 1 pt de plus
T,X,Y = Lissajous(p,q,np.pi/2,N+1)
# on enleve le dernier point (periodicite)
per = T[-1]
print("periode : ",per," N =",N)
parametres 4 7
periode : 28.0 N = 512
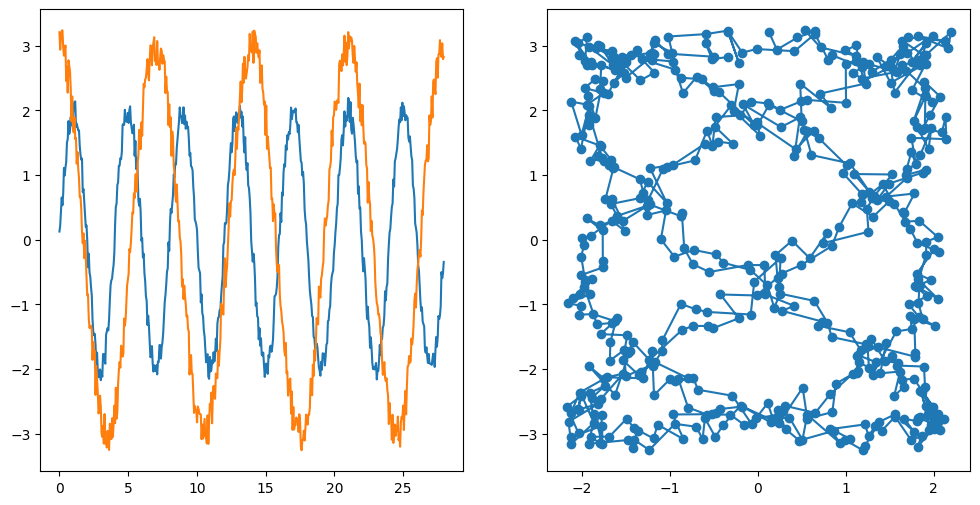
# données bruitées
T = T[:-1]
X = 2*X[:-1]
Y = 3*Y[:-1]
X1 = X + 0.2*(2*np.random.rand(X.size)-1)
Y1 = Y + 0.3*(2*np.random.rand(Y.size)-1)
plt.figure(figsize=(12,6))
plt.subplot(1,2,1)
plt.plot(T,X1,T,Y1)
plt.subplot(1,2,2)
plt.plot(X1,Y1,'-o')
[<matplotlib.lines.Line2D at 0x7fadadcf2f80>]
1.9.1. analyse des données par FFT#
calcul de la FFT du signal discret
détermination des pics
calcul du spectre de puissance, i.e. l’amplitude en fonction de la frequence
calcul de l’amplitude et de la phase
# analayse de Fourier
from scipy.fftpack import fft
N = X.size
dt = T[1]-T[0]
XF = fft(X1)
YF = fft(Y1)
# amplitude et frequence
PFX = (2./N)*np.abs(XF[0:N//2])
PFY = (2./N)*np.abs(YF[0:N//2])
# attention calcul frequence
FF = np.linspace(0.,1./(2*dt),N//2,endpoint=False)
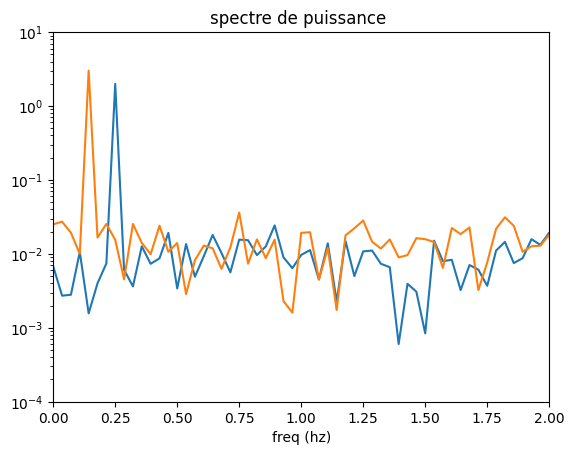
# spectre
plt.semilogy(FF,PFX,FF,PFY)
plt.ylim([1.e-4,10.])
plt.xlim([0.,2.])
plt.xlabel('freq (hz)')
plt.title('spectre de puissance ')
Text(0.5, 1.0, 'spectre de puissance ')
# determination du pic de frequence
print("Determination de la frequence fondamentale (pic du spectre)")
imX = np.argmax(PFX)
ax1 = PFX[imX]
wx1 = 2*np.pi*FF[imX]
phix1 = np.angle(XF[imX])
px1 = round(1./FF[imX])
print("X pulsation {:.5g} amplitude {:.5g} phase:{:.5g} p={} ({:.5g})".format(wx1,ax1,phix1,px1,1./FF[imX]))
imY = np.argmax(PFY)
ay1 = PFY[imY]
wy1 = 2*np.pi*FF[imY]
phiy1 = np.angle(YF[imY])
py1 = round(1./FF[imY])
print("Y pulsation {:.5g} amplitude {:.5g} phase:{:.5g} p={} ({:.5g})".format(wy1,ay1,phiy1,py1,1./FF[imY]))
Determination de la frequence fondamentale (pic du spectre)
X pulsation 1.5708 amplitude 1.9924 phase:-1.578 p=4 (4)
Y pulsation 0.8976 amplitude 3.0144 phase:-0.0041078 p=7 (7)
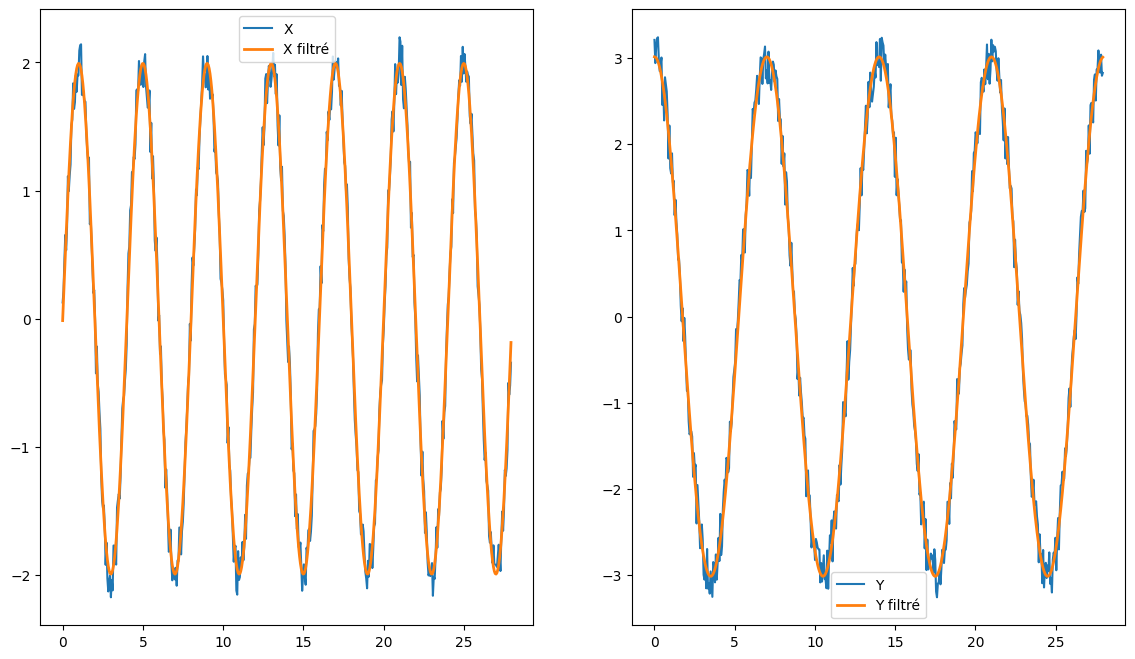
plt.figure(figsize=(14,8))
plt.subplot(1,2,1)
plt.plot(T,X1,label='X')
plt.plot(T,ax1*np.cos(wx1*T+phix1),lw=2,label='X filtré')
plt.legend()
plt.subplot(1,2,2)
plt.plot(T,Y1,label='Y')
plt.plot(T,ay1*np.cos(wy1*T+phiy1),lw=2,label='Y filtré')
plt.legend()
<matplotlib.legend.Legend at 0x7fad9b666740>
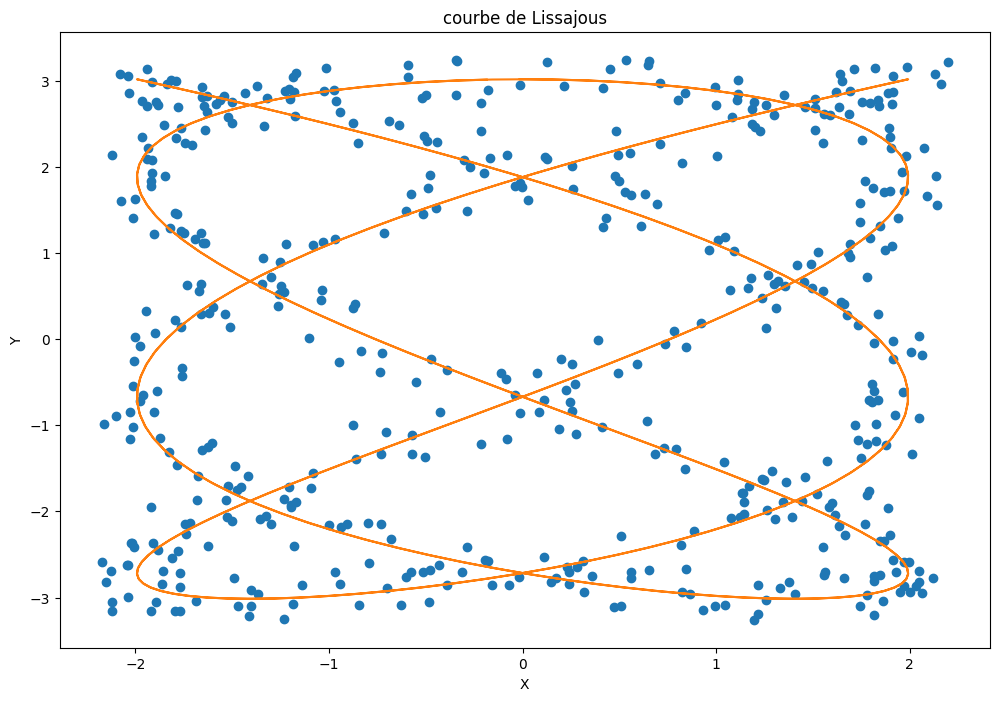
plt.figure(figsize=(12,8))
plt.plot(X1,Y1,'o')
plt.plot(ax1*np.cos(wx1*T+phix1),ay1*np.cos(wy1*T+phiy1))
plt.xlabel('X')
plt.ylabel('Y')
plt.title('courbe de Lissajous')
Text(0.5, 1.0, 'courbe de Lissajous')
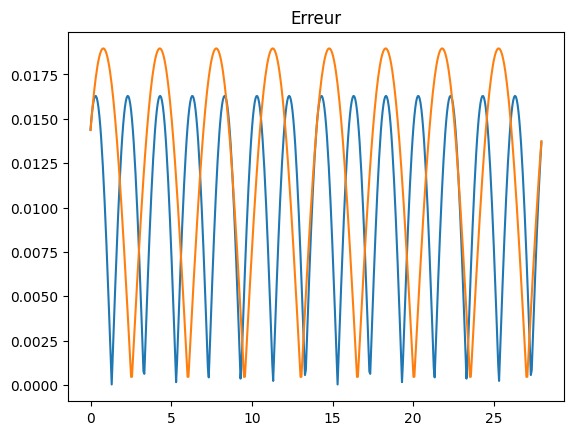
errx = np.abs(ax1*np.cos(wx1*T+phix1)-X)
erry = np.abs(ay1*np.cos(wy1*T+phiy1)-Y)
plt.plot(T,errx,T,erry)
plt.title('Erreur');
