Modélisation d’un pendule double par IA

7.9. Modélisation d’un pendule double par IA#

Marc Buffat, dpt mécanique, Lyon 1

inspiré de Deep Learning with Real Data and the Chaotic Double Pendulum on https://cloud4scieng.org

Pendule double

7.9.1. Problème#

Expérience du double pendule

7.9.2. Modélisation mécanique#

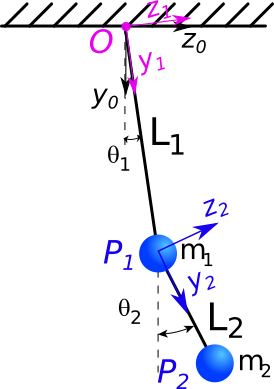
On doit donc définir:

  1. les parametres du problème: longueur et masse des 2 pendules \(l_1,m_1,l_2,m_2\)

  2. les 2 ddl du problème: \(\theta_1(t)\) et \(\theta_2(t)\)

Système conservatif: équation de Lagrange

(7.2)#\[\begin{align} \alpha \left( \beta \omega_{1}^{2} \sin{(\theta_{1})} + \beta \frac{d^{2}\theta_{1}}{d t^{2}} + \omega_{1}^{2} \sin{(\theta_{1})} + \frac{d^{2}\theta_{1}}{d t^{2}} \right) + \sin{(\theta_{1} - \theta_{2})} \left(\frac{d\theta_{2}}{d t}\right)^{2} + \cos{(\theta_{1} - \theta_{2})} \frac{d^{2}}{d t^{2}} \theta_{2} = 0\\ \alpha \omega_{1}^{2} \sin{\theta_{2}} - \alpha \sin{(\theta_{1} - \theta_{2})} \left(\frac{d \theta_{1}}{d t}\right)^{2} + \alpha \cos{(\theta_{1}- \theta_{2})} \frac{d^{2} \theta_{1}}{d t^{2}} + \frac{d^{2} \theta_{2}}{d t^{2}} = 0 \end{align}\]

7.9.2.1. Simulation numérique#

Pour résoudre numériquement ce système, nous devons le transformer en un système d’équations différentielles du premier ordre.

On choisit comme vecteur d’état \(U = [\theta_1, \dot{\theta_1},\theta_2, \dot{\theta_2}]\), et on écrit le système sous la forme $\( \dot{U} = \mathbf{F} U\)$

7.9.2.2. Modèle numérique#

  • \(u_0 =[\theta_1(0),0.,\theta_2(0),0.]\) conditions initiales (dim=4)

vecteur d’état \(V ~=~ [\theta_1, \dot{\theta_1}, \theta_2, \dot{\theta_2} ]\)

  • u[0] = angle du premier pendule

  • u[1] = vitesse angulaire du premier pendule

  • u[2] = angle du second pendule

  • u[3] = vitesse angulaire du second pendule

Le vector \(V ~=~ [\theta_1, u_1, \theta_2, u_2 ]\) contient les 2 angles \(\theta_1\) et \(\theta_2\) et les vitesses angulaires \(u_1\) and \(u_2\)

\[ u_1 = \frac{d \theta_1}{dt} \mbox{ et } u_2 = \frac{d \theta_2}{dt} \]

En posant \(c=cos(\theta_1 - \theta_2 )\) et \(s = sin(\theta_1 - \theta_2 )\)

\[ \frac{d u_1}{dt} ~=~ \frac{m_2 g sin(\theta_2)c - m_2 s ( L_1c u_1^2 + L_2 u_2^2 )- (m_1+m_2)g sin(\theta_1)}{ L_1 (m_1+m_2s^2)} \]
\[ \frac{d u_2}{dt} ~=~ \frac{(m_1+m_2)(L_1u_1^2s - gsin(u_2) + gsin(u_1)c) + m_2L_2u_2^2sc)}{L_2 (m_1+m_2s^2)} \]

7.9.2.3. Paramètres de l’étude#

  • paramètres \(m_1,m_2,L_1,L_2,g\)

  • calcul de la solution en N temps équi-répartis

7.9.2.4. Résolution numérique#

7.9.2.5. Calcul de la solution#

png

png

7.9.3. Objectif#

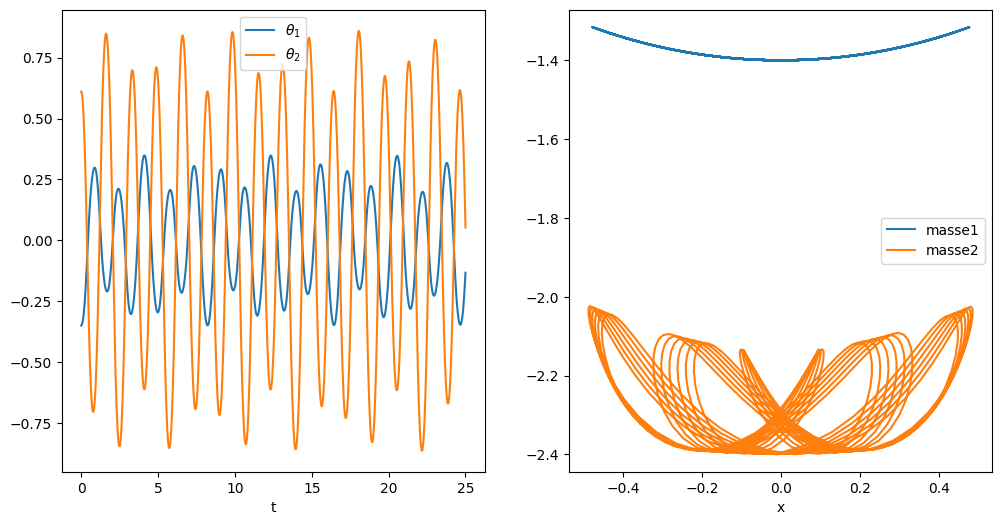
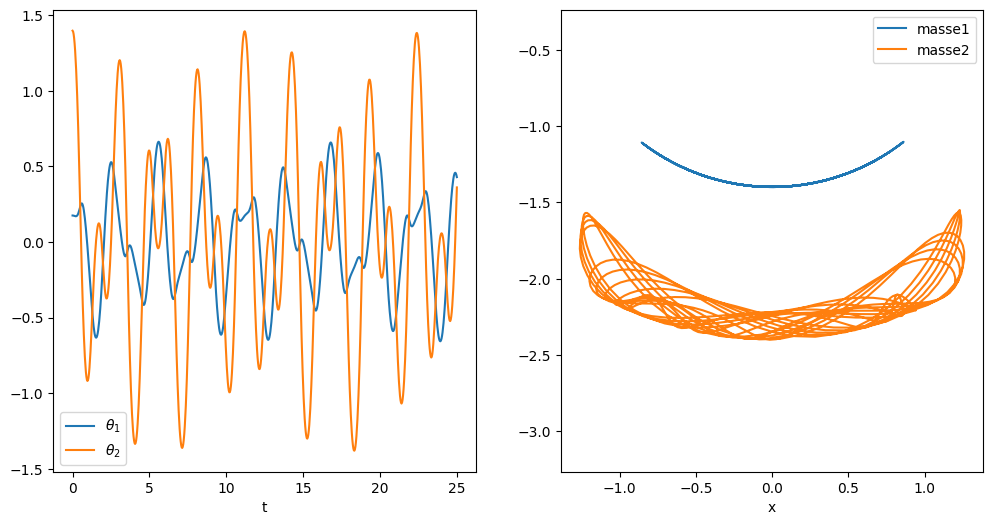
Peut on prédire la trajectoire du système sans faire la simulation, en utilisant un apprentissage à partir d’une base de données issue de la simulation.

7.9.3.1. prédiction#

En se donnant la valeur de solution sur 10 valeurs en temps consécutives, peut on prédire l’évolution de la solution sur des temps longs: p.e. sur les 100 pas en temps suivants

7.9.3.2. base de données#

Pour créer la base de données, on découpe la simulation avec une fenêtre glissante de 10 valeurs en temps consécutives pour prédire la valeur de la solution à l’instant t

\[ sol(t) = \mathbf{F}\left(sol(t-\Delta t),sol(t-2\Delta t),..sol(t-10\Delta t)\right) \]

7.9.4. Base de données d’apprentissage#

  • train_seq: données (data) tableau dim (10,4)

  • train_label: résultat dim (4)

création de la BD avec une technique de fenêtre glissante et d’adimensionalisation

BD: 741
valeurs BD: (tensor([[-1.0000e+00,  8.2172e-04,  7.1066e-01, -4.9913e-04],
        [-9.9434e-01,  8.7259e-02,  7.0519e-01, -8.1255e-02],
        [-9.7731e-01,  1.7447e-01,  6.8877e-01, -1.6236e-01],
        [-9.4877e-01,  2.6318e-01,  6.6132e-01, -2.4412e-01],
        [-9.0847e-01,  3.5398e-01,  6.2273e-01, -3.2680e-01],
        [-8.5612e-01,  4.4723e-01,  5.7288e-01, -4.1047e-01],
        [-7.9139e-01,  5.4281e-01,  5.1165e-01, -4.9485e-01],
        [-7.1403e-01,  6.3974e-01,  4.3898e-01, -5.7900e-01],
        [-6.2400e-01,  7.3561e-01,  3.5504e-01, -6.6078e-01],
        [-5.2172e-01,  8.2584e-01,  2.6040e-01, -7.3621e-01]]), tensor([[-0.4084,  0.9032,  0.1563, -0.7990]]))

7.9.5. Modèle LSTM#

réseau de neuronnes récurrents: LSTM « neural network » nn de pyTorch

paramétres

  • taille des données élémentaires input_size= 4 : 4 données / temps = \(\theta_1, \theta_2, \dot{\theta_1},\dot{\theta_2} \)

  • nbre de couches de neuronnes cachés (depliement de la récurrence en temps) hidden_size=100 pas en temps

  • optimisation: méthode d’optimisation par gradient, algorithme stochastique de gradient d’ADAM

  • utilisation des états précédents (états cn (long-term memory) et états cachés hn (short-term memory))

     lstm = nn.LSTM(input_size, hidden_size, num_LSTM=1)
 
 output, (hn,cn) = lstm(input, (h0,c0))

attention pytorch a sa propre version des tableaux (torch tensor)

  • conversion données: tableau 1D 100 -> sortie dim 4

       Linear(100, 4)

apprentissage

  • à partir de la base de données initiale: simulation (751,4)

  • fenêtrage: 741 fenêtres glissantes (10,5) -> (4)

  • on choisit au hasard 500 fenêtres pour faire l’apprentissage ( pour 1 passage)

  • on réitère le processus complet epochs fois. epochs est un hyperparamètre qui définit le nombre de fois que l’algorithme d’apprentissage parcours l’ensemble des données d’entraînement. Ce paramétre peut etre très grand !

7.9.5.1. Apprentissage#

recalcul model:lstm-pend1 nbepochs=52


/home/buffat/venvs/jupyter/lib/python3.10/site-packages/torch/autograd/__init__.py:200: UserWarning: CUDA initialization: The NVIDIA driver on your system is too old (found version 9010). Please update your GPU driver by downloading and installing a new version from the URL: http://www.nvidia.com/Download/index.aspx Alternatively, go to: https://pytorch.org to install a PyTorch version that has been compiled with your version of the CUDA driver. (Triggered internally at ../c10/cuda/CUDAFunctions.cpp:109.)
  Variable._execution_engine.run_backward(  # Calls into the C++ engine to run the backward pass


epoch:   1 loss: 0.01505351
seq:   1 loss: 3.25216733
epoch:   3 loss: 0.00025682
seq:   3 loss: 0.18376897
epoch:   5 loss: 0.00014668
seq:   5 loss: 0.21797341
epoch:   7 loss: 0.00075469
seq:   7 loss: 0.11024632
epoch:   9 loss: 0.00024955
seq:   9 loss: 0.12144019
epoch:  11 loss: 0.00021650
seq:  11 loss: 0.09058059
epoch:  13 loss: 0.00007820
seq:  13 loss: 0.10575360
epoch:  15 loss: 0.00017686
seq:  15 loss: 0.42198471
epoch:  17 loss: 0.00006502
seq:  17 loss: 0.10770231
epoch:  19 loss: 0.00010987
seq:  19 loss: 0.13459274
epoch:  21 loss: 0.00007744
seq:  21 loss: 0.21146205
epoch:  23 loss: 0.00029414
seq:  23 loss: 0.21190936
epoch:  25 loss: 0.00047763
seq:  25 loss: 0.10344179
epoch:  27 loss: 0.00022167
seq:  27 loss: 0.04047549
epoch:  29 loss: 0.00066361
seq:  29 loss: 0.07751106
epoch:  31 loss: 0.00032528
seq:  31 loss: 0.09540407
epoch:  33 loss: 0.00085075
seq:  33 loss: 0.10937494
epoch:  35 loss: 0.00001382
seq:  35 loss: 0.03735177
epoch:  37 loss: 0.00001100
seq:  37 loss: 0.11880642
epoch:  39 loss: 0.00006818
seq:  39 loss: 0.06761478
epoch:  41 loss: 0.00003622
seq:  41 loss: 0.03080786
epoch:  43 loss: 0.00003321
seq:  43 loss: 0.11387769
epoch:  45 loss: 0.00020217
seq:  45 loss: 0.07403137
epoch:  47 loss: 0.00011312
seq:  47 loss: 0.05696190
epoch:  49 loss: 0.00000965
seq:  49 loss: 0.09897501
epoch:  51 loss: 0.00054223
seq:  51 loss: 0.06909767
FIN epoch:  51 loss: 0.0005422260

7.9.5.2. Prédiction du model#

  • à partir de données data, on utilise les train_window=10 données initiales pour prédire la solution aux steps=100 pas en temps suivants

  • test sur la base de données d’apprentissage avec steps=100 et steps=200

  • test sur une autre base de données

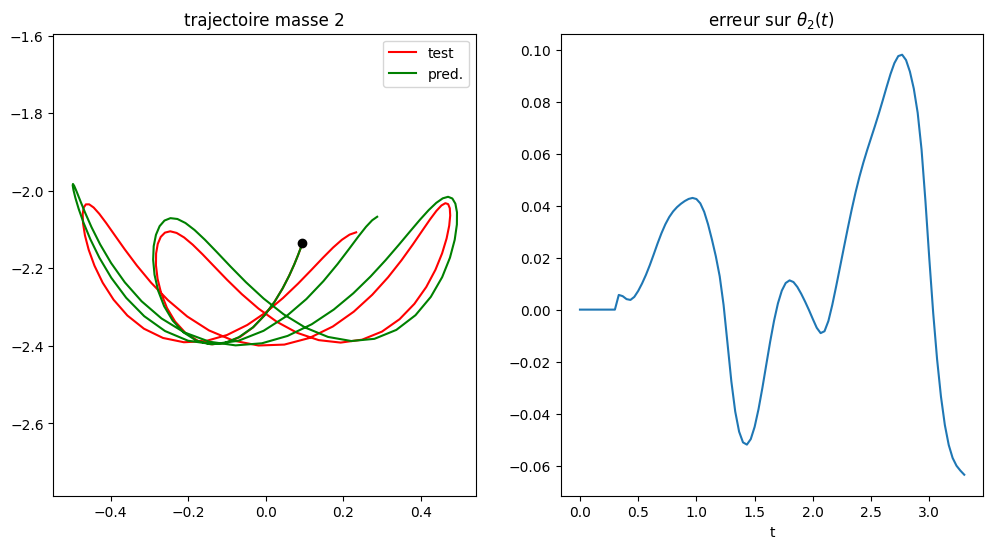
    data set length = 751 pred= 100 mean error = 0.031581153573318775 maxerr = 0.0980479744670017 at 83

7.9.5.3. test sur base de donnée de test#

data set length = 751 pred= 100
mean error = 0.031581153573318775
maxerr = 0.0980479744670017  at  83

png

data set length = 751 pred= 200
mean error = 0.08418902912197787
maxerr = 0.29675144719920316  at  185

png

7.9.5.4. prédiction d’une nouvelle simulation#

data set length = 751 pred= 100
mean error = 0.09653476548880306
maxerr = 0.3060819799157  at  93

png

data set length = 751 pred= 100
mean error = 0.31714558863685754
maxerr = 1.1709687741336705  at  93

png

7.9.6. Conclusion#

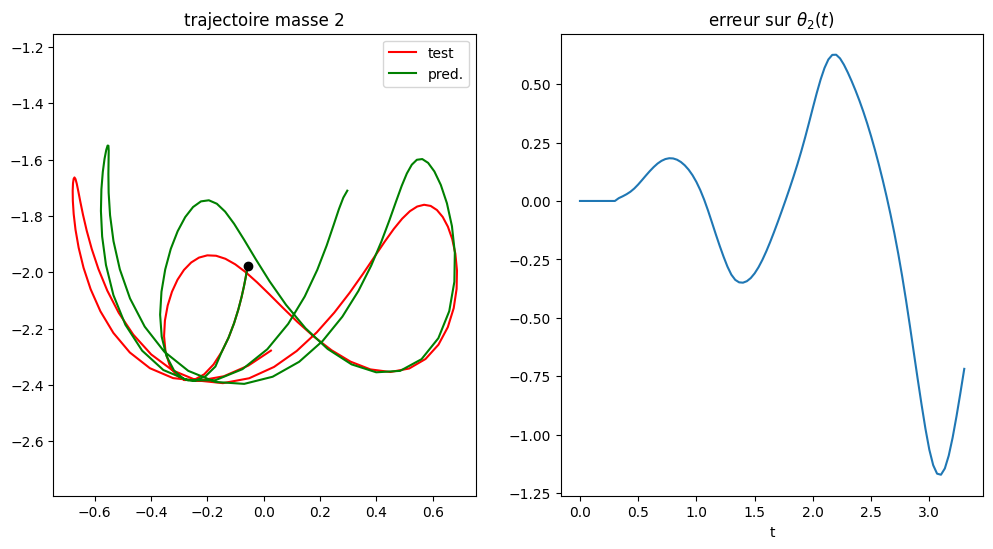
Nous remarquons que l’apprentissage LSTM avec une unique solution permettait au LSTM de générer des solutions raisonnablement bonnes à partir de points proches du point initial de la solution.

7.9.7. Amélioration: Physics-Informed Neural Networks (PINN)#

  1. contrainte sur l’évolutionn du système :

  • système conservatif: Ec + Ep = cste

\[ E(\theta_1, \theta_2, \dot{\theta_1}, \dot{\theta_2}) = cste\]

  • minimisation sous contrainte

  1. Réseaux de neuronnes inspiré par la physique !!!

c’est nouvelle classe de réseaux de neurones qui hybride apprentissage automatique et lois physiques permettant une « meilleur » prédiction des réseaux de neuronnes (Deep Learning) pour des applications physiques gérées par des équations (ODE ou PDE):

7.9.8. FIN#

Contenu