7.2. TP OUTPUT Planification: étude d’un pont roulant

ERREUR: numéro d’étudiant non spécifié!!!

Login étudiant Toto toto uid=137764122

parametres de la trajectoire: Xf=7.0 L0=7.0 Lf=8.0 Lm=4.0 alpha=0.8

7.2.1. Modélisation

7.2.1.1. objectif

On veut déplacer, à l’aide d’un système de levage par câble (grue ou pont roulant), une charge d’un endroit à un autre en évitant les oscillations résiduelles à l’arrivée. L’objectif est de proposer une stratégie de commande simple et réaliste qui repose sur une structure de commande hiérarchisée, composée de régulateurs de bas niveau rapides, simples et découplés et d’une commande de haut niveau lente et prenant en compte les couplages. En outre, on mesure la position et la vitesse du chariot ainsi que la position et la vitesse du treuil, mais la position de la charge n’est pas mesurée. C’est pourquoi nous ne considérons que des bouclages qui ne dépendent que des positions et vitesses du chariot et du treuil.

Le cas d’une trajectoire simple avec un cable de longueur constante \(L_0\) sera traiter ensemble en début de TP et vous aurez à traiter ensuite les 2 cas suivants avec les paramètres individuels données plus haut.

• trajectoire ascendente directe avec levage du cable de \(L_0\) à \(L_f\) (de A à B)

• trajectoire avec un obstacle nécessitant un levage du cable à \(L_m\) (de A à B en passant par C) (optionnel)

On vous demandera de rédiger un CR succinct sur ces 2 cas dans le fichier monCR.tex sur la stratégie de contrôle mise en place pour minimiser les oscillations de la charge en fin de trajectoire.

7.2.1.2. modélisation

• modèle mécanique = masse ponctuelle P (masse) et chariot (C)

pendule P de masse m de longueur \(l(t)\) accroché à un chariot C de masse M se deplacant horizontalement \(x_c(t)\)

• système à 3 ddl \(xc(t), \theta(t), l(t) \)

• treuil de rayon \(\rho\)

  • rayon \(\rho\) (on néglige son inertie \(J_\rho\))

  • angle \(\phi = (l-l_0)/\rho\)

7.2.1.3. Définition des repères et ddl

• définir les ddl avec dynamicsymbols

• définir les paramètres avec symbols

• définir les repères RO, RP ReferencePoint et les points O, P et C Point

  “C=”

\(\displaystyle x_{c}\mathbf{\hat{r_o}_x}\)

'P='

\(\displaystyle - l\mathbf{\hat{r_p}_y} + x_{c}\mathbf{\hat{r_o}_x}\)

7.2.1.4. cinématique

• calcul vitesse des points P et C

• définition des masses ponctuelles Pc et Pa associées au chariot et à la masse m Particle

• calcul de l’energie potentielle

\(\displaystyle \dot{x}_{c}\mathbf{\hat{r_o}_x}\)

\(\displaystyle - \dot{l}\mathbf{\hat{r_p}_y}\)

\(\displaystyle l \dot{\theta}\mathbf{\hat{r_p}_x} - \dot{l}\mathbf{\hat{r_p}_y} + \dot{x}_{c}\mathbf{\hat{r_o}_x}\)

\(\displaystyle \frac{m \left(l \cos{\left(\theta \right)} \dot{\theta} + \sin{\left(\theta \right)} \dot{l}\right) \dot{x}_{c}}{2} + \frac{m l^{2} \dot{\theta}^{2}}{2} + \frac{m l \cos{\left(\theta \right)} \dot{\theta} \dot{x}_{c}}{2} + \frac{m \sin{\left(\theta \right)} \dot{l} \dot{x}_{c}}{2} + \frac{m \dot{l}^{2}}{2} + \frac{m \dot{x}_{c}^{2}}{2}\)

\(\displaystyle - g m l \cos{\left(\theta \right)}\)

7.2.1.5. Lagrangien

• calcul du lagrangien du système chariot+masse dans La Lagrangian

\(\displaystyle \frac{M \dot{x}_{c}^{2}}{2} + g m l \cos{\left(\theta \right)} + \frac{m l^{2} \dot{\theta}^{2}}{2} + m l \cos{\left(\theta \right)} \dot{\theta} \dot{x}_{c} + m \sin{\left(\theta \right)} \dot{l} \dot{x}_{c} + \frac{m \dot{l}^{2}}{2} + \frac{m \dot{x}_{c}^{2}}{2}\)

7.2.1.6. Bilan des forces

• force motrice \(F\) sur le chariot en C

• force de tension \(T\) dans le cable (ne travaille pas)

• couple sur un treuil de rayon \(\rho\)

  • couple \(C\)

  • travail \(C_t \rho \delta l \)

• \(\alpha = \frac{M}{m}\) rapport des masses

• adimensionalisation:

  • \( F = F_c M = F_c\alpha m \)

  • \( C = C_t m \rho \)

• définition d’un repère Rt lié au treuil

• calcul angle \(\phi_t\) en fct de \(l(t)\) (enroulement autour du treuil)

• \(l_0\) longueur de référence

7.2.1.7. Equations de Lagrange

calcul des équations de Lagrange LagrangesMethod avec le travail des forces extérieures

• force de traction du chariot Fc

• couple sur le treuil Ct

\(\displaystyle \frac{M \dot{x}_{c}^{2}}{2} + g m l \cos{\left(\theta \right)} + \frac{m l^{2} \dot{\theta}^{2}}{2} + m l \cos{\left(\theta \right)} \dot{\theta} \dot{x}_{c} + m \sin{\left(\theta \right)} \dot{l} \dot{x}_{c} + \frac{m \dot{l}^{2}}{2} + \frac{m \dot{x}_{c}^{2}}{2}\)

\(\displaystyle \left[\begin{matrix}m \left(g \sin{\left(\theta \right)} + l \ddot{\theta} + \cos{\left(\theta \right)} \ddot{x}_{c} + 2 \dot{l} \dot{\theta}\right) l\\- F_{c} M + M \ddot{x}_{c} - m l \sin{\left(\theta \right)} \dot{\theta}^{2} + m l \cos{\left(\theta \right)} \ddot{\theta} + m \sin{\left(\theta \right)} \ddot{l} + 2 m \cos{\left(\theta \right)} \dot{l} \dot{\theta} + m \ddot{x}_{c}\\m \left(C_{t} - g \cos{\left(\theta \right)} - l \dot{\theta}^{2} + \sin{\left(\theta \right)} \ddot{x}_{c} + \ddot{l}\right)\end{matrix}\right]\)

7.2.2. Chariot mobile, longueur fixe

• on applique une force motrice horizontale \(F_c\) avec un cable de longueur \(l_0\) fixe

• adim: \( F_c M = F_c \alpha m \)

• \(\alpha = \frac{M}{m}\)

• objectif:

  • déterminer la force \(F_c\) pour avoir un ballant minimum

  • tests de différents contrôle

    • contrôle du chariot seule

    • asservissement de la trajectoire du chariot

    • couplage de haut niveau

• calcul du nouveau lagrangien

• calcul des equations de lagranges

• introduction de \(\alpha = M/m\)

\(\displaystyle \frac{m \left(\alpha \dot{x}_{c}^{2} + 2 g l_{0} \cos{\left(\theta \right)} + l_{0}^{2} \dot{\theta}^{2} + 2 l_{0} \cos{\left(\theta \right)} \dot{\theta} \dot{x}_{c} + \dot{x}_{c}^{2}\right)}{2}\)

\(\displaystyle \left[\begin{matrix}l_{0} m \left(g \sin{\left(\theta \right)} + l_{0} \ddot{\theta} + \cos{\left(\theta \right)} \ddot{x}_{c}\right)\\m \left(- F_{c} \alpha + \alpha \ddot{x}_{c} - l_{0} \sin{\left(\theta \right)} \dot{\theta}^{2} + l_{0} \cos{\left(\theta \right)} \ddot{\theta} + \ddot{x}_{c}\right)\end{matrix}\right]\)

7.2.2.1. 1ere methode: contrôle simple du chariot

On contrôle uniquement le chariot \(x_c(t)\) sans tenir compte de l’interaction avec la masse P: on suppose que \(\theta \approx 0=cste\)

L’équation du mouvement du chariot s’écrit alors

\[ (1+\alpha)\ddot{x_c} = \alpha F_c\]

• on impose une trajectoire simple au chariot tq. $\( x_c(0)=0, \dot{x_c}(0)=0, x_c(t_f) = x_f, \dot{x_c}(t_f)=0\)$

• d’où \(x_c(t)\) polynôme de degré 3

\[ x_c(t) = x_f \frac{t^2}{t_f^2}(3-2\frac{t}{t_f})\]

• d’où la force \(F_c\) sur le chariot

• definition analytique

• conversion fonction python avec lambdify

  “xc=”

\(\displaystyle \frac{t^{2} x_{f} \left(- 2 t + 3 t_{f}\right)}{t_{f}^{3}}\)

\(\displaystyle \left( x_{f}, \ 0\right)\)

'Fc='

\(\displaystyle - \frac{2 x_{f} \left(\alpha + 1\right) \left(6 t - 3 t_{f}\right)}{\alpha t_{f}^{3}}\)

7.2.2.2. 2ieme méthode: asservissement simple

• on applique un asservissement simple pour avoir la trajectoire précédente

\[ x_i(t) = x_f \frac{t^2}{t_f^2}(3-2\frac{t}{t_f})\]

• asservissement $\( F_a(t) = -K_c \left( (x(t)-x_i(t)) + T_c(\dot x - \dot x_i) \right) \)$

\(\displaystyle - K_{c} \left(T_{c} \left(\frac{2 t^{2} x_{f}}{t_{f}^{3}} - \frac{2 t x_{f} \left(- 2 t + 3 t_{f}\right)}{t_{f}^{3}} + \dot{x}_{c}\right) - \frac{t^{2} x_{f} \left(- 2 t + 3 t_{f}\right)}{t_{f}^{3}} + x_{c}\right)\)

7.2.2.3. 3ieme méthode: commande de haut niveau lente

• linéarisation des équations

• contrôle du positionnement de la charge P

• calcul de la commande en fonction du mvt de la charge

7.2.2.3.1. mouvement de la charge

• calcul des coordonnées de la charge P: \(\xi(t)\), \(\eta(t)\) dans le repère fixe

• relation entre \(\theta\) \(\xi\) et \(\eta\)

\(\displaystyle (l \sin{\left(\theta \right)} + x_{c})\mathbf{\hat{r_o}_x} - l \cos{\left(\theta \right)}\mathbf{\hat{r_o}_y}\)

\(\displaystyle \xi = l \sin{\left(\theta \right)} + x_{c}\)

\(\displaystyle \eta = - l \cos{\left(\theta \right)}\)

\(\displaystyle \tan{\left(\theta \right)} = \frac{x_{c} - \xi}{\eta}\)

7.2.2.3.2. paramétrisation / trajectoire

• équation d’équilibre de la charge en fonction de la tension T

• réécrire les équations du mvt pour obtenir \(\theta\) et \(x_c\) en fct de \(\xi\) et \(\eta\)

\(\displaystyle m \ddot{\xi} = - T \sin{\left(\theta \right)}\)

\(\displaystyle m \ddot{\eta} = T \cos{\left(\theta \right)} - g m\)

\(\displaystyle \tan{\left(\theta \right)} = - \frac{\ddot{\xi}}{g + \ddot{\eta}}\)

\(\displaystyle x_{c} = \xi - \frac{\eta \ddot{\xi}}{g + \ddot{\eta}}\)

7.2.2.3.3. paramétrisation

si on connait \(\xi(t)\) et \(\eta(t)\) jusqu’à leurs dérivées d’ordre 4, peut donc déterminer le mouvement et calculer la force \(F_c\) “on doit calculer \(\ddot{x_c}\) et \(\ddot{\theta\)}$

idée on va déterminer le mouvement de la masse M (i.e. \(\xi(t)\) et \(\eta(t)\)) pour pouvoir en déduire la force \(F_c\). Pour cela on va se placer dans le cas de petites oscillations (linéarisation)

7.2.2.3.4. linéarisation \(\theta\) petit

• \(\eta = - l_0\)

• \(\theta = -\frac{\ddot{\xi}}{g}\)

• \(x_c = \xi + \frac{l_0}{g} \ddot{\xi}\)

• \(\omega_0 ^2 = \frac{g}{l_0}\)

calcul de la force \(F_c\) dans ce cas en fct de \(\xi(t)\) et \(\omega_0\)

\(\displaystyle - F_{c} \alpha + \alpha \ddot{x}_{c} + l_{0} \ddot{\theta} + \ddot{x}_{c}\)

\(\displaystyle - F_{c} \alpha + \alpha \left(\ddot{\xi} + \frac{\ddddot{\xi}}{\omega_{0}^{2}}\right) + \ddot{\xi}\)

'Fc='

\(\displaystyle F_{c} = \frac{\alpha \left(\ddot{\xi} + \frac{\ddddot{\xi}}{\omega_{0}^{2}}\right) + \ddot{\xi}}{\alpha}\)

7.2.2.3.5. choix de la trajectoire \(\xi(t)\) la plus régulière t.q.

On veut que la masse M soit immobile au départ et à l’arrivée

• trajectoire \(\xi(t)\) idéale tq. $\(\xi(0)=0, \frac{d\xi}{dt}(0)=0, \frac{d^2\xi}{dt^2}(0)=0, \frac{d^3\xi}{dt^3}(0)=0, \frac{d^4\xi}{dt^4}(0)=0\)\( \)\(\xi(t_f)=x_f, \frac{d\xi}{dt}(t_f)=0, \frac{d^2\xi}{dt^2}(t_f)=0, \frac{d^3\xi}{dt^3}(t_f)=0, \frac{d^4\xi}{dt^4}(t_f)=0\)$

• \(\xi(t)\) polynome de degré 9 en t

\[\xi(t) = x_f(\frac{t}{t_f})^5 (126-420(\frac{t}{t_f})+540(\frac{t}{tf})^2-315(\frac{t}{t_f})^3+70(\frac{t}{tf})^4)\]

\(\displaystyle \xi = \frac{t^{5} x_{f} \left(\frac{70 t^{4}}{t_{f}^{4}} - \frac{315 t^{3}}{t_{f}^{3}} + \frac{540 t^{2}}{t_{f}^{2}} - \frac{420 t}{t_{f}} + 126\right)}{t_{f}^{5}}\)

dérivées en tf: 0 0 0 0

\(\displaystyle F_{c} = \frac{2520 t x_{f} \left(2 \alpha \omega_{0}^{2} t^{6} - 7 \alpha \omega_{0}^{2} t^{5} t_{f} + 9 \alpha \omega_{0}^{2} t^{4} t_{f}^{2} - 5 \alpha \omega_{0}^{2} t^{3} t_{f}^{3} + \alpha \omega_{0}^{2} t^{2} t_{f}^{4} + 84 \alpha t^{4} - 210 \alpha t^{3} t_{f} + 180 \alpha t^{2} t_{f}^{2} - 60 \alpha t t_{f}^{3} + 6 \alpha t_{f}^{4} + 2 \omega_{0}^{2} t^{6} - 7 \omega_{0}^{2} t^{5} t_{f} + 9 \omega_{0}^{2} t^{4} t_{f}^{2} - 5 \omega_{0}^{2} t^{3} t_{f}^{3} + \omega_{0}^{2} t^{2} t_{f}^{4}\right)}{\alpha \omega_{0}^{2} t_{f}^{9}}\)

\(\displaystyle x_{c} = \frac{t^{3} x_{f} \left(70 \omega_{0}^{2} t^{6} - 315 \omega_{0}^{2} t^{5} t_{f} + 540 \omega_{0}^{2} t^{4} t_{f}^{2} - 420 \omega_{0}^{2} t^{3} t_{f}^{3} + 126 \omega_{0}^{2} t^{2} t_{f}^{4} + 5040 t^{4} - 17640 t^{3} t_{f} + 22680 t^{2} t_{f}^{2} - 12600 t t_{f}^{3} + 2520 t_{f}^{4}\right)}{\omega_{0}^{2} t_{f}^{9}}\)

\(\displaystyle \theta = \frac{2520 t^{3} x_{f} \left(- 2 t^{4} + 7 t^{3} t_{f} - 9 t^{2} t_{f}^{2} + 5 t t_{f}^{3} - t_{f}^{4}\right)}{l_{0} \omega_{0}^{2} t_{f}^{9}}\)

7.2.2.4. Parametres de la simulation

• définition des paramètres

• attention valeur des parametres KC et TC

\[\ddot{x_c} = -K_c\left((x_c - x_i) + T_c(\dot{x_c}- \dot{x_i})\right)\]

optimal si \(\Delta=0\) i.e. \(Tc^2 = 4/K_c\)

7.2.2.5. parametres trajectoire: Xf=7.0 L0=7.0 Lf=8.0 Lm=4.0 alpha=0.8

Simulation:  100.0 0.2 4.0 3.4746094143618937

7.2.2.6. tracée de la solution idéale \(\xi(t)\)

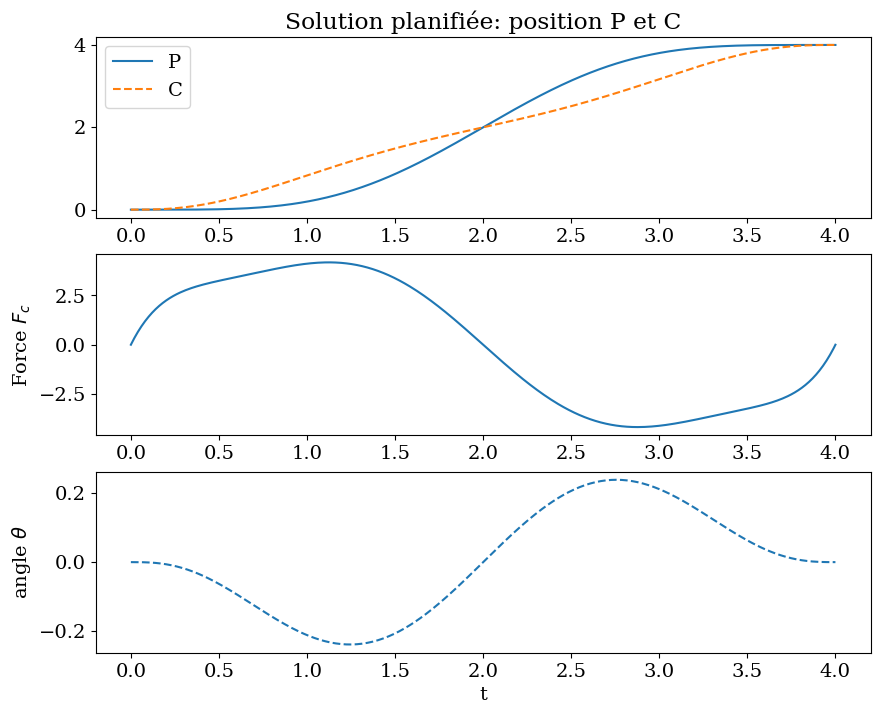
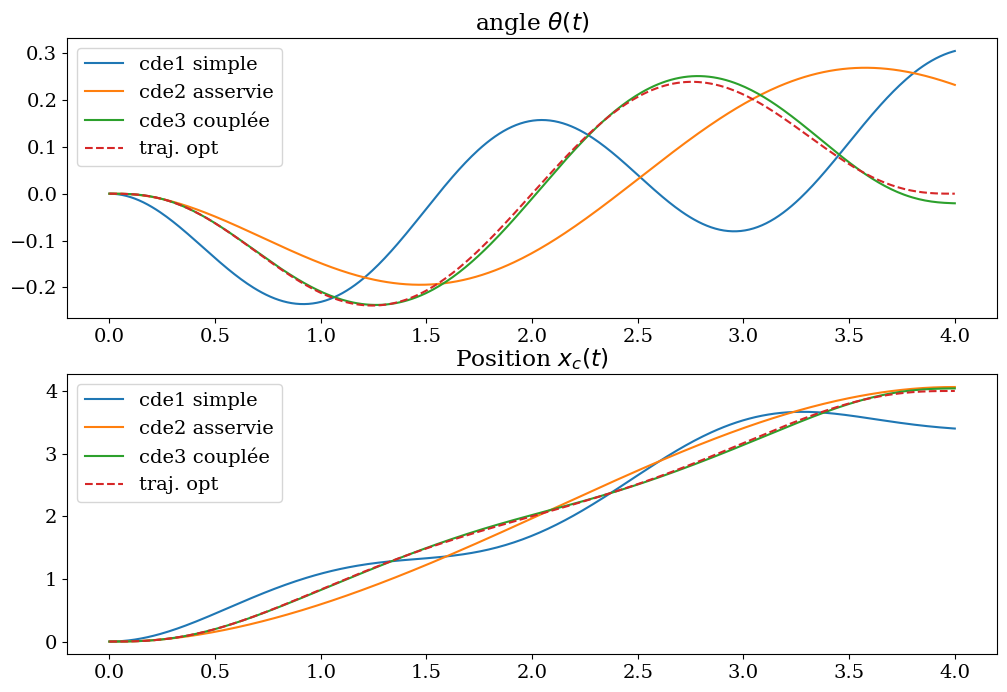
7.2.2.7. Simulation avec les 3 contrôles

• commande simple Fs

• asservissement simple Fa

• commande lente couplée F

définition du second membre des equations de lagrange sous forme EDO du 1er ordre

\[ \dot{Y} = F(Y,t)\]

'Equations Lagrange:'

\(\displaystyle \left[\begin{matrix}- \frac{m \left(- 2 g l_{0} \sin{\left(\theta \right)} - 2 l_{0} \sin{\left(\theta \right)} \dot{\theta} \dot{x}_{c}\right)}{2} + \frac{m \left(2 l_{0}^{2} \ddot{\theta} - 2 l_{0} \sin{\left(\theta \right)} \dot{\theta} \dot{x}_{c} + 2 l_{0} \cos{\left(\theta \right)} \ddot{x}_{c}\right)}{2}\\- F_{c} \alpha m + \frac{m \left(2 \alpha \ddot{x}_{c} - 2 l_{0} \sin{\left(\theta \right)} \dot{\theta}^{2} + 2 l_{0} \cos{\left(\theta \right)} \ddot{\theta} + 2 \ddot{x}_{c}\right)}{2}\end{matrix}\right]\)

'F(Y)='

\(\displaystyle \left[\begin{matrix}\dot{\theta}\\\dot{x}_{c}\\- \frac{F_{c} \alpha \cos{\left(\theta \right)} + \alpha g \sin{\left(\theta \right)} + g \sin{\left(\theta \right)} + \frac{l_{0} \sin{\left(2 \theta \right)} \dot{\theta}^{2}}{2}}{l_{0} \left(\alpha + \sin^{2}{\left(\theta \right)}\right)}\\\frac{F_{c} \alpha + \frac{g \sin{\left(2 \theta \right)}}{2} + l_{0} \sin{\left(\theta \right)} \dot{\theta}^{2}}{\alpha + \sin^{2}{\left(\theta \right)}}\end{matrix}\right]\)

'F(Y)='

\(\displaystyle \left[\begin{matrix}\dot{\theta}\\\dot{x}_{c}\\\frac{- F_{c} \alpha \cos{\left(\theta \right)} - \alpha l_{0} \omega_{0}^{2} \sin{\left(\theta \right)} - l_{0} \omega_{0}^{2} \sin{\left(\theta \right)} - \frac{l_{0} \sin{\left(2 \theta \right)} \dot{\theta}^{2}}{2}}{l_{0} \left(\alpha + \sin^{2}{\left(\theta \right)}\right)}\\\frac{F_{c} \alpha + \frac{l_{0} \omega_{0}^{2} \sin{\left(2 \theta \right)}}{2} + l_{0} \sin{\left(\theta \right)} \dot{\theta}^{2}}{\alpha + \sin^{2}{\left(\theta \right)}}\end{matrix}\right]\)

3.0 1.8083141320025125 0.5 4.0 4.0
Erreur sur la position finale
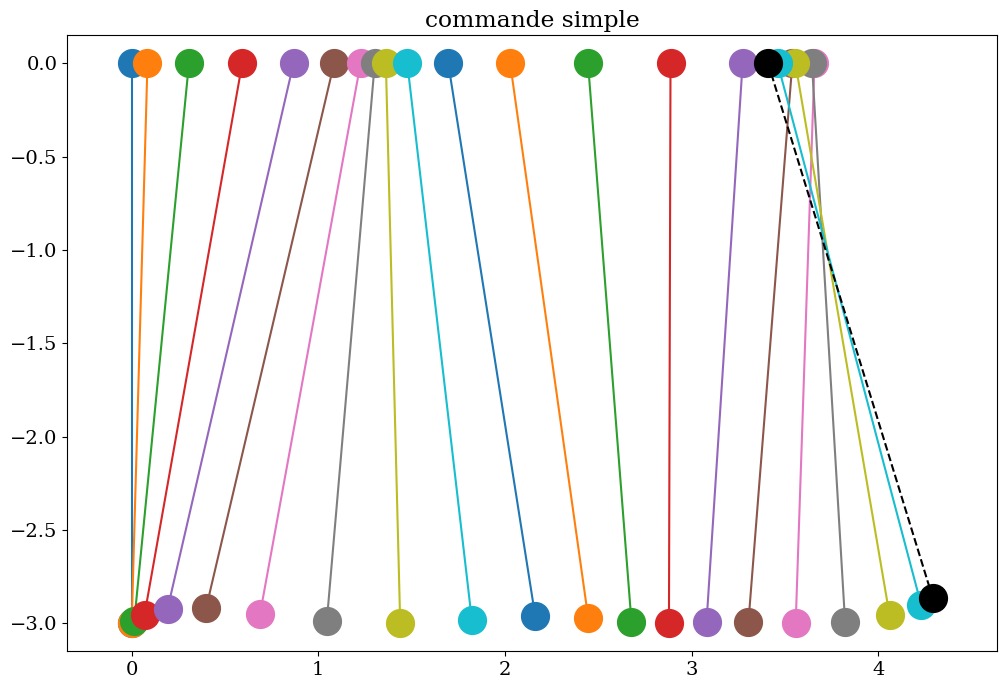
commande 1 simple   erreur xc=-0.5999 	 theta=17.455 deg
commande 2 asservie erreur xc=0.0632 	 theta=13.309 deg
commande 3 couplée  erreur xc=0.0410 	 theta=-1.175 deg

7.2.2.8. analyse solution commande simple

Once Loop Reflect

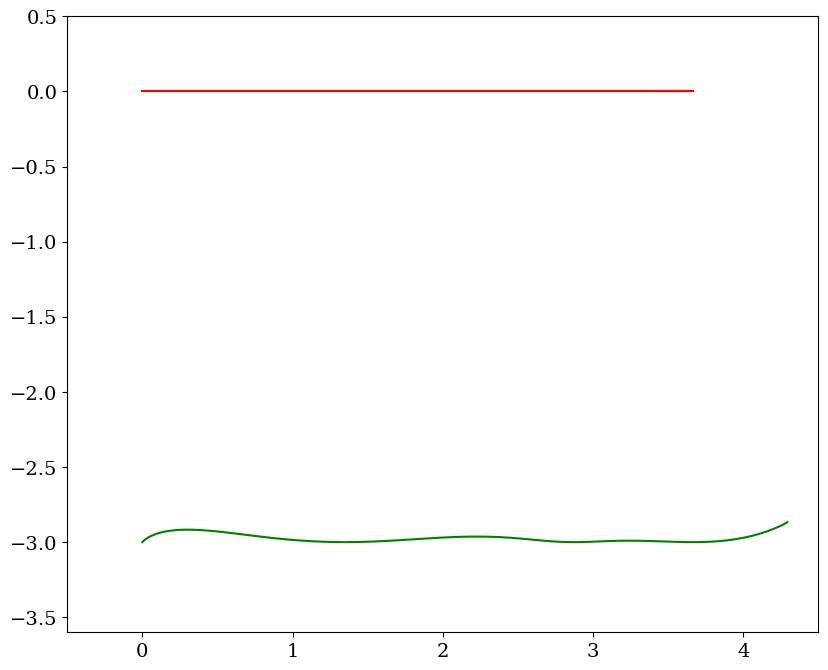
7.2.2.9. analyse solution commande asservie

Once Loop Reflect

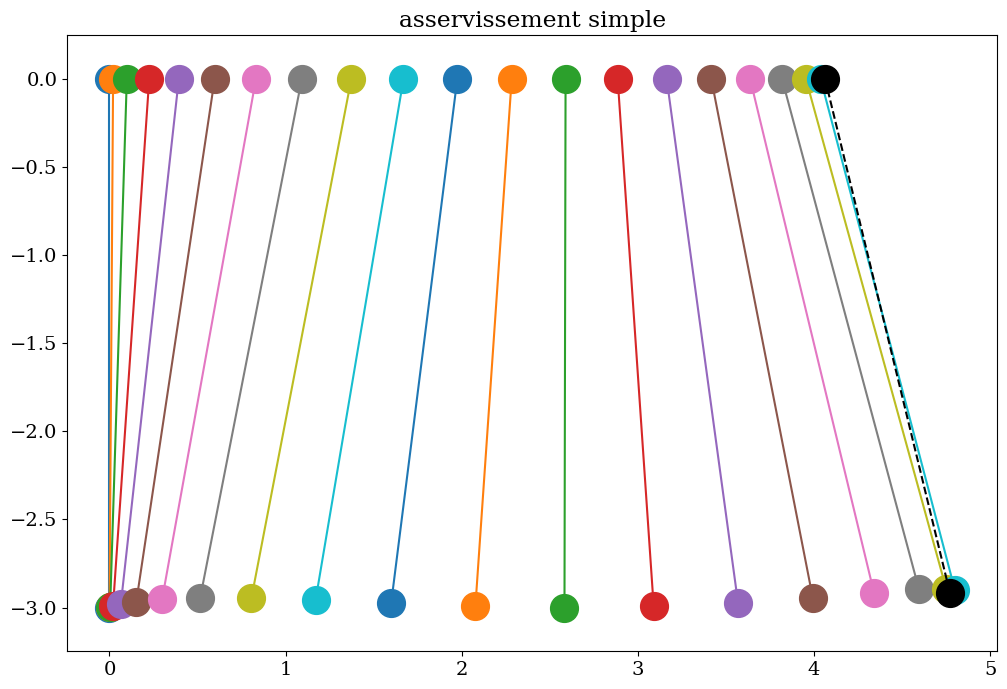
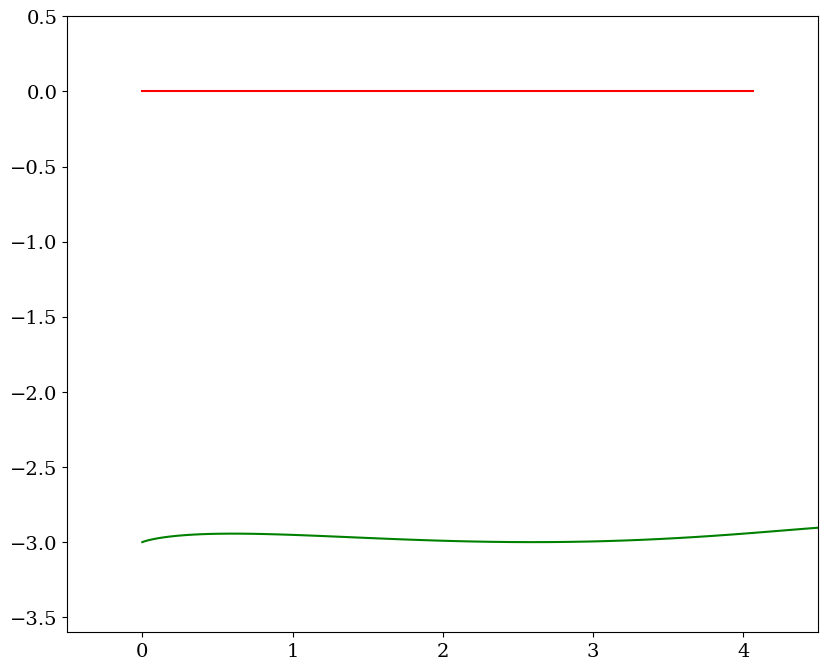
7.2.2.10. analyse solution commande couplée

Once Loop Reflect

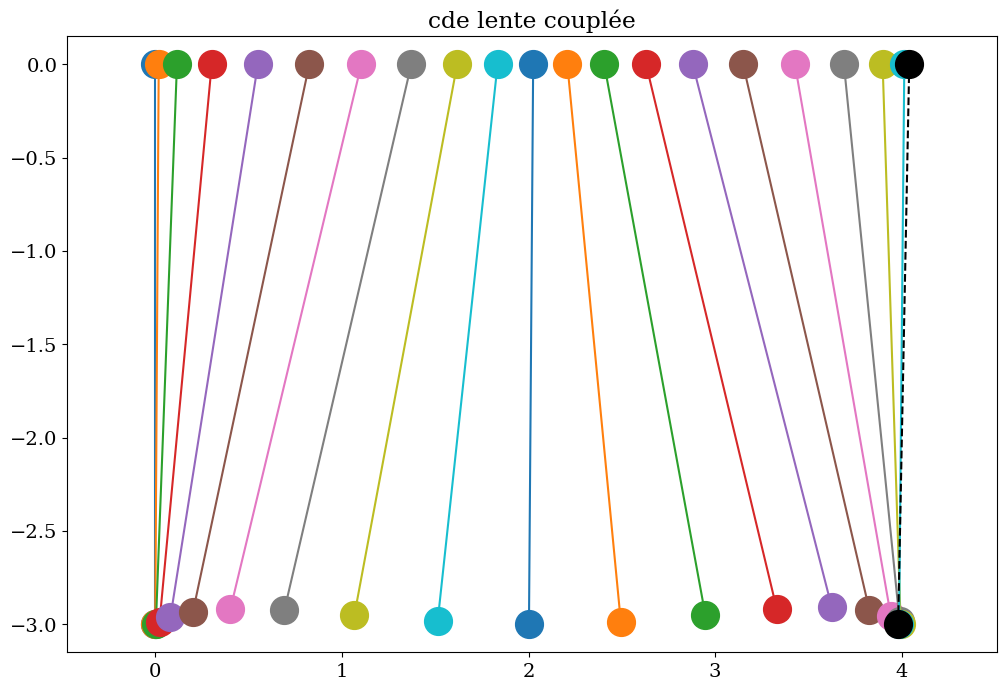
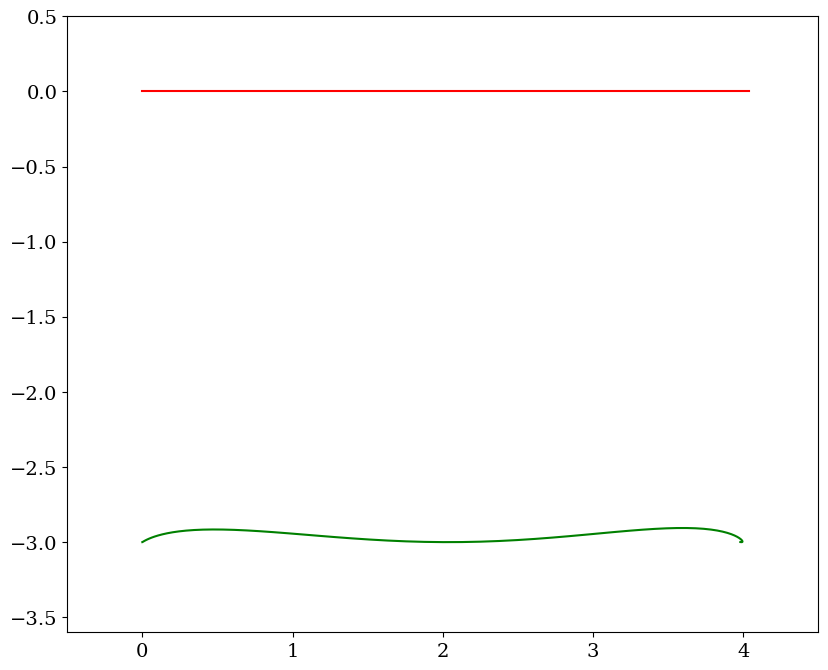
7.2.3. Asservissement: regulateur bas niveau

pour rendre la commande précédente robuste on ajoute un asservissement pour suivre la trajectoire idéale

• trajectoire imposée \(x_i(t)\) à partir de \(\xi(t)\) $\(x_i(t) = \xi + \frac{l_0}{g} \ddot{\xi}\)$

• au lieu d’imposer directement la trajectoire, on ajoute un régulateur à la cde précédente $\( F_c = F_i -K_c ( (x_c-x_i) + T_c(\dot{x_c}-\dot{x_i})) \)$

\(\displaystyle \frac{t^{3} x_{f} \left(70 \omega_{0}^{2} t^{6} - 315 \omega_{0}^{2} t^{5} t_{f} + 540 \omega_{0}^{2} t^{4} t_{f}^{2} - 420 \omega_{0}^{2} t^{3} t_{f}^{3} + 126 \omega_{0}^{2} t^{2} t_{f}^{4} + 5040 t^{4} - 17640 t^{3} t_{f} + 22680 t^{2} t_{f}^{2} - 12600 t t_{f}^{3} + 2520 t_{f}^{4}\right)}{\omega_{0}^{2} t_{f}^{9}}\)

\(\displaystyle - K_{c} \left(T_{c} \left(\dot{x}_{c} - \frac{t^{3} x_{f} \left(420 \omega_{0}^{2} t^{5} - 1575 \omega_{0}^{2} t^{4} t_{f} + 2160 \omega_{0}^{2} t^{3} t_{f}^{2} - 1260 \omega_{0}^{2} t^{2} t_{f}^{3} + 252 \omega_{0}^{2} t t_{f}^{4} + 20160 t^{3} - 52920 t^{2} t_{f} + 45360 t t_{f}^{2} - 12600 t_{f}^{3}\right)}{\omega_{0}^{2} t_{f}^{9}} - \frac{3 t^{2} x_{f} \left(70 \omega_{0}^{2} t^{6} - 315 \omega_{0}^{2} t^{5} t_{f} + 540 \omega_{0}^{2} t^{4} t_{f}^{2} - 420 \omega_{0}^{2} t^{3} t_{f}^{3} + 126 \omega_{0}^{2} t^{2} t_{f}^{4} + 5040 t^{4} - 17640 t^{3} t_{f} + 22680 t^{2} t_{f}^{2} - 12600 t t_{f}^{3} + 2520 t_{f}^{4}\right)}{\omega_{0}^{2} t_{f}^{9}}\right) + x_{c} - \frac{t^{3} x_{f} \left(70 \omega_{0}^{2} t^{6} - 315 \omega_{0}^{2} t^{5} t_{f} + 540 \omega_{0}^{2} t^{4} t_{f}^{2} - 420 \omega_{0}^{2} t^{3} t_{f}^{3} + 126 \omega_{0}^{2} t^{2} t_{f}^{4} + 5040 t^{4} - 17640 t^{3} t_{f} + 22680 t^{2} t_{f}^{2} - 12600 t t_{f}^{3} + 2520 t_{f}^{4}\right)}{\omega_{0}^{2} t_{f}^{9}}\right)\)

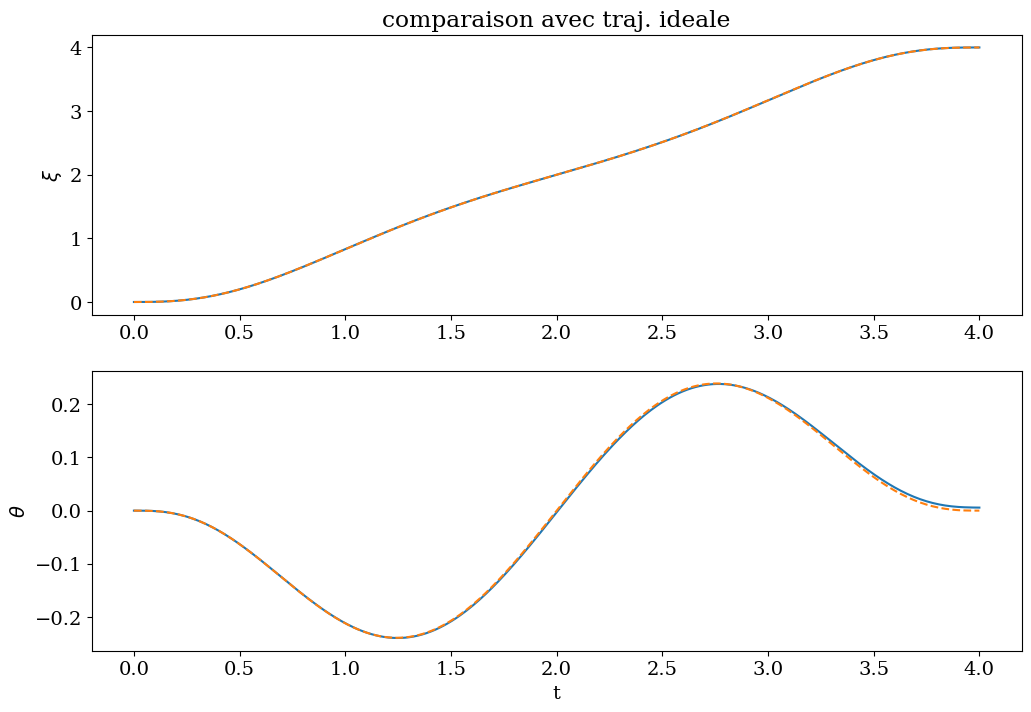
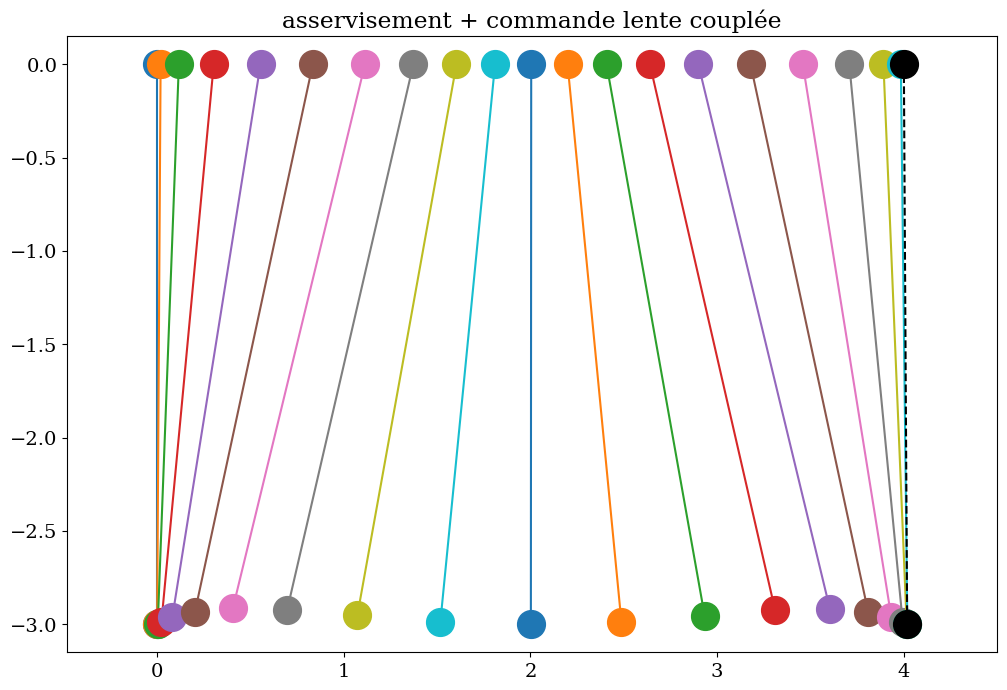
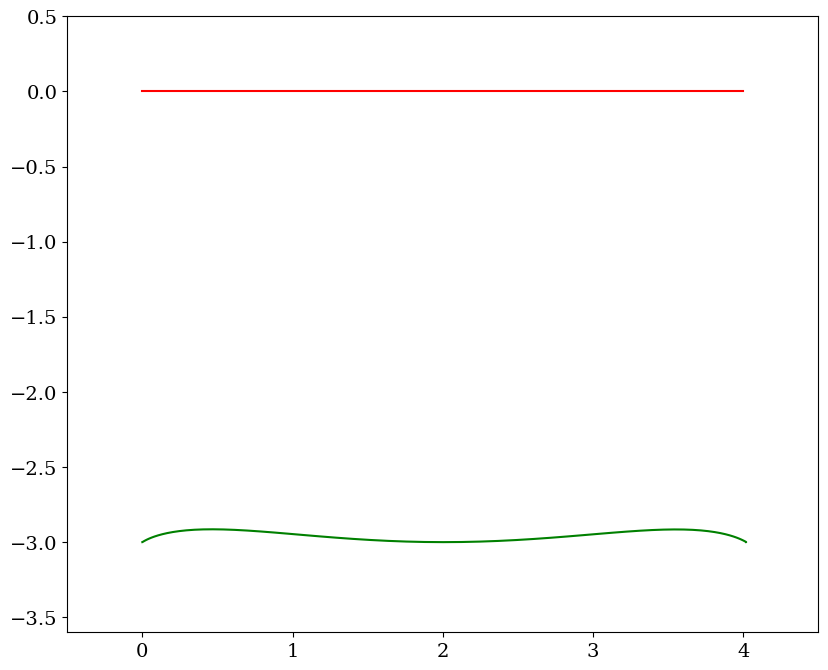
7.2.3.1. simulation

calculer la commande FC = cde idéale + asservissement

parametres: 200 0.1414213562373095 4.0
Erreur sur la position finale
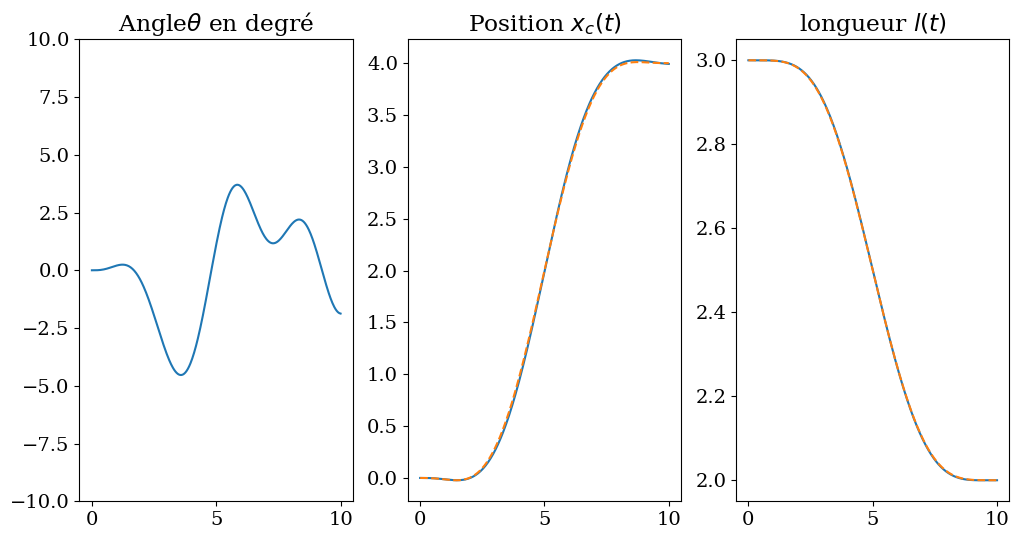
commande couplée  erreur xc=0.001 	 theta=0.325 deg

Once Loop Reflect

7.2.4. Chariot mobile et longueur de cable variable

7.2.4.1. mouvement de la charge

• coordonnees \(\xi(t)\), \(\eta(t)\) dans le repere fixe (voir cours) $\(\xi = l \sin\theta + x-c \)\( \)\(\eta = -l \cos\theta \)$

• équations d’équilibre $\( m\ddot\xi = -T \sin\theta\)\( \)\( m\ddot\xi = -T \sin\theta\)$

• d’où l’expression de \(\theta\), \(l\) et \(x_c\) en fonction de \(\xi\) et \(\eta\)

\[ \tan \theta = \frac{\ddot{\xi}}{\ddot{\eta}-g}\]

\[ x_c = \xi - \frac{\eta\ddot{\xi}}{\ddot{\eta}-g}\]

\[ (\xi - x_c)^2 + \eta^2 = l^2 \]

• trajectoire idéale

on planifie une trajectoire idéale pour \(\xi\) et \(\eta\) , et on en déduit la valeur de \(x_c(t)\) \(\theta(t)\) et \(l(t)\), et le contrôle associé

• trajectoire rectiligne AB

\(\displaystyle \tan{\left(\theta \right)} = \frac{\ddot{\xi}}{- g + \ddot{\eta}}\)

\(\displaystyle x_{c} = \xi - \frac{\eta \ddot{\xi}}{- g + \ddot{\eta}}\)

7.2.4.1.1. trajectoire planifiée

on utilise la trajectoire planifiée précédente pour \(\xi(t)\)

• trajectoire \(\xi(t)\) tq. $\(\xi(0)=0, \frac{d\xi}{dt}(0)=0, \frac{d^2\xi}{dt^2}(0)=0, \frac{d^3\xi}{dt^3}(0)=0, \frac{d^4\xi}{dt^4}(0)=0\)\( \)\(\xi(t_f)=x_f, \frac{d\xi}{dt}(t_f)=0, \frac{d^2\xi}{dt^2}(t_f)=0, \frac{d^3\xi}{dt^3}(t_f)=0, \frac{d^4\xi}{dt^4}(t_f)=0\)$

• \(\xi(t)\) polynome de degré 9 en t

pour la trajectoire \(\eta(t)\) (même condition que \(\xi\)) sauf sur la position

• \(\eta=-l_0\) longueur à \(t=0\)

• \(\eta=-l_f\) longueur à \(t=t_f\)

\(\displaystyle \xi = \frac{t^{5} x_{f} \left(\frac{70 t^{4}}{t_{f}^{4}} - \frac{315 t^{3}}{t_{f}^{3}} + \frac{540 t^{2}}{t_{f}^{2}} - \frac{420 t}{t_{f}} + 126\right)}{t_{f}^{5}}\)

dérivées en tf: 0 0 0 0

\(\displaystyle \eta = - l_{0} - \frac{t^{5} \left(- l_{0} + l_{f}\right) \left(\frac{70 t^{4}}{t_{f}^{4}} - \frac{315 t^{3}}{t_{f}^{3}} + \frac{540 t^{2}}{t_{f}^{2}} - \frac{420 t}{t_{f}} + 126\right)}{t_{f}^{5}}\)

7.2.4.2. cas linéaire

on suppose que \(\theta \approx 0\)

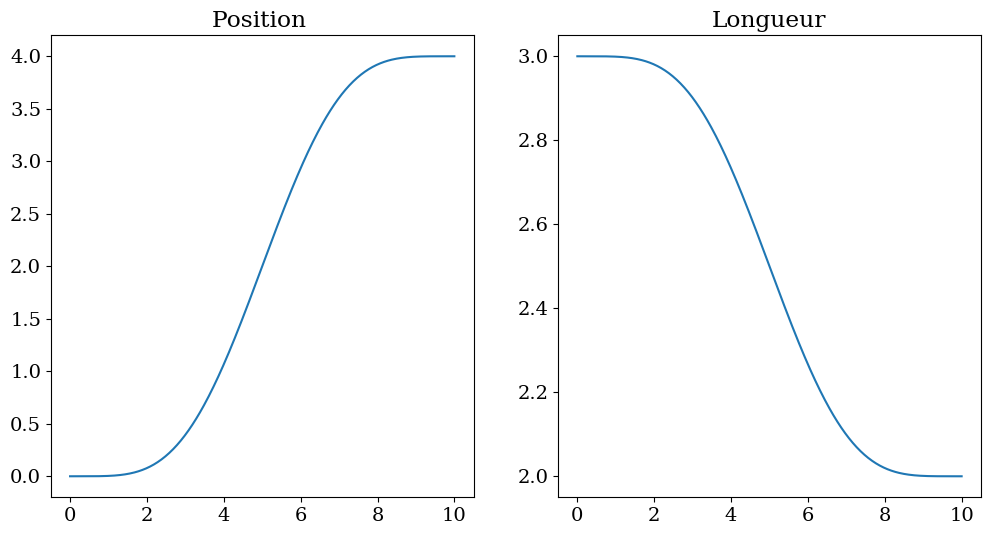
trajectoire idéale du chariot et du cable : $\(x_{ref}(t) \approx \xi(t) \)\( \)\(l_{ref}(t) \approx - \eta(t)\)$

d’ou l’asservissement de \(F_c\) et \(C_t\)

\[ F_c = -K_c ( (x-x_{ref}) + T_c (\dot{x}-\dot{x}_{ref})) \]

\[ C_t = -g -K_t ( (l-l_{ref}) + T_t (\dot{l}-\dot{l}_{ref})) \]

'trajectoire idéale:'

\(\displaystyle \frac{t^{5} x_{f} \left(\frac{70 t^{4}}{t_{f}^{4}} - \frac{315 t^{3}}{t_{f}^{3}} + \frac{540 t^{2}}{t_{f}^{2}} - \frac{420 t}{t_{f}} + 126\right)}{t_{f}^{5}}\)

\(\displaystyle l_{0} + \frac{t^{5} \left(- l_{0} + l_{f}\right) \left(\frac{70 t^{4}}{t_{f}^{4}} - \frac{315 t^{3}}{t_{f}^{3}} + \frac{540 t^{2}}{t_{f}^{2}} - \frac{420 t}{t_{f}} + 126\right)}{t_{f}^{5}}\)

\(\displaystyle \frac{K_{c} \left(630 T_{c} t^{8} x_{f} - 2520 T_{c} t^{7} t_{f} x_{f} + 3780 T_{c} t^{6} t_{f}^{2} x_{f} - 2520 T_{c} t^{5} t_{f}^{3} x_{f} + 630 T_{c} t^{4} t_{f}^{4} x_{f} - T_{c} t_{f}^{9} \dot{x}_{c} + 70 t^{9} x_{f} - 315 t^{8} t_{f} x_{f} + 540 t^{7} t_{f}^{2} x_{f} - 420 t^{6} t_{f}^{3} x_{f} + 126 t^{5} t_{f}^{4} x_{f} - t_{f}^{9} x_{c}\right)}{t_{f}^{9}}\)

\(\displaystyle \frac{K_{t} \left(- T_{t} \left(5 t^{5} \left(l_{0} - l_{f}\right) \left(56 t^{3} - 189 t^{2} t_{f} + 216 t t_{f}^{2} - 84 t_{f}^{3}\right) + 5 t^{4} \left(l_{0} - l_{f}\right) \left(70 t^{4} - 315 t^{3} t_{f} + 540 t^{2} t_{f}^{2} - 420 t t_{f}^{3} + 126 t_{f}^{4}\right) + t_{f}^{9} \dot{l}\right) - t^{5} \left(l_{0} - l_{f}\right) \left(70 t^{4} - 315 t^{3} t_{f} + 540 t^{2} t_{f}^{2} - 420 t t_{f}^{3} + 126 t_{f}^{4}\right) + t_{f}^{9} \left(l_{0} - l\right)\right) - g t_{f}^{9}}{t_{f}^{9}}\)

7.2.4.3. Equation lagrange avec couple

\(\displaystyle \frac{m \left(\alpha \dot{x}_{c}^{2} + 2 g l \cos{\left(\theta \right)} + l^{2} \dot{\theta}^{2} + 2 l \cos{\left(\theta \right)} \dot{\theta} \dot{x}_{c} + 2 \sin{\left(\theta \right)} \dot{l} \dot{x}_{c} + \dot{l}^{2} + \dot{x}_{c}^{2}\right)}{2}\)

\(\displaystyle \left[\begin{matrix}m \left(g \sin{\left(\theta \right)} + l \ddot{\theta} + \cos{\left(\theta \right)} \ddot{x}_{c} + 2 \dot{l} \dot{\theta}\right) l\\m \left(- F_{c} \alpha + \alpha \ddot{x}_{c} - l \sin{\left(\theta \right)} \dot{\theta}^{2} + l \cos{\left(\theta \right)} \ddot{\theta} + \sin{\left(\theta \right)} \ddot{l} + 2 \cos{\left(\theta \right)} \dot{l} \dot{\theta} + \ddot{x}_{c}\right)\\m \left(- C_{t} - g \cos{\left(\theta \right)} - l \dot{\theta}^{2} + \sin{\left(\theta \right)} \ddot{x}_{c} + \ddot{l}\right)\end{matrix}\right]\)

\(\displaystyle \left[\begin{matrix}\dot{\theta}\\\dot{x}_{c}\\\dot{l}\\\frac{\frac{C_{t} \sin{\left(2 \theta \right)}}{2} - F_{c} \alpha \cos{\left(\theta \right)} - \alpha g \sin{\left(\theta \right)} - 2 \alpha \dot{l} \dot{\theta}}{\alpha l}\\- \frac{C_{t} \sin{\left(\theta \right)}}{\alpha} + F_{c}\\C_{t} + \frac{C_{t} \sin^{2}{\left(\theta \right)}}{\alpha} - F_{c} \sin{\left(\theta \right)} + g \cos{\left(\theta \right)} + l \dot{\theta}^{2}\end{matrix}\right]\)

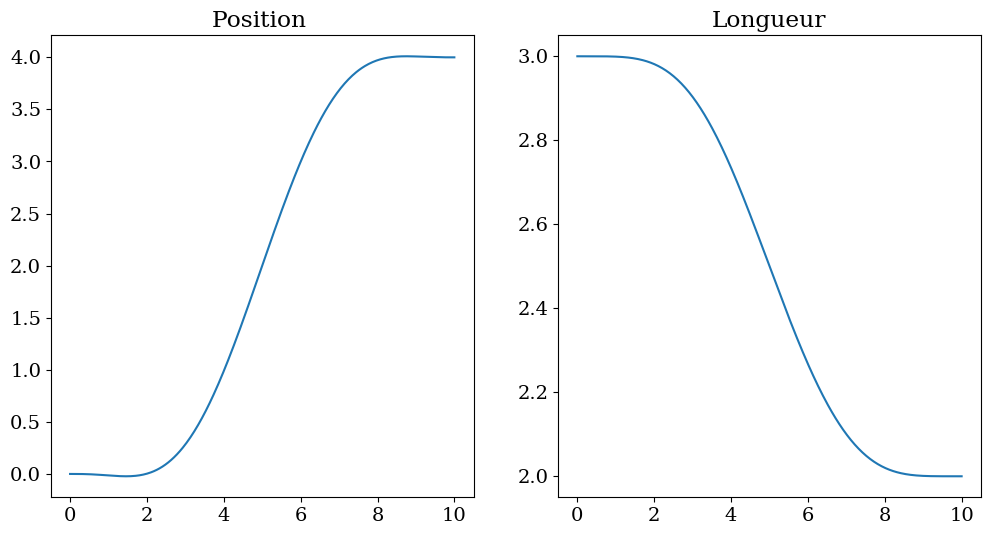
7.2.4.4. Simulation de la trajectoire

7.2.4.5. parametres trajectoire: Xf=7.0 L0=7.0 Lf=8.0 Lm=4.0 alpha=0.8

Text(0.5, 1.0, 'Longueur')

7.2.5. cas non linéaire

• ddl fonction de la trajectoire (idéale) \(\xi\) \(\eta\) $\( x_{ref} = \xi - \frac{\eta\ddot{\xi}}{\ddot{\eta}-g}\)$

\[ l_{ref} = \sqrt{(\frac{\eta\ddot{\xi}}{\ddot{\eta}-g})^2 + \eta^2}\]

t**5*x_f*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5 - 10*t**3*x_f*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/(t_f**5*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)) sqrt(100*t**6*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)**2/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + (-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2)


-K_c*(T_c*(-t**5*x_f*(280*t**3/t_f**4 - 945*t**2/t_f**3 + 1080*t/t_f**2 - 420/t_f)/t_f**5 - 5*t**4*x_f*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5 + 10*t**3*x_f*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(560*t**3/t_f**4 + 3*t**2*(56*t/t_f**2 - 63/t_f)/t_f**2 - 1890*t**2/t_f**3 + 5*t*(168*t**2/t_f**3 - 378*t/t_f**2 + 216/t_f)/t_f + 6*t*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 2160*t/t_f**2 + 5*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840/t_f)/(t_f**5*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)) + 10*t**3*x_f*(-t**5*(-l_0 + l_f)*(280*t**3/t_f**4 - 945*t**2/t_f**3 + 1080*t/t_f**2 - 420/t_f)/t_f**5 - 5*t**4*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/(t_f**5*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)) + 10*t**3*x_f*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(-10*t**3*(l_0 - l_f)*(560*t**3/t_f**4 + 3*t**2*(56*t/t_f**2 - 63/t_f)/t_f**2 - 1890*t**2/t_f**3 + 5*t*(168*t**2/t_f**3 - 378*t/t_f**2 + 216/t_f)/t_f + 6*t*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 2160*t/t_f**2 + 5*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840/t_f)/t_f**5 - 30*t**2*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/(t_f**5*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + 30*t**2*x_f*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/(t_f**5*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)) + Derivative(x_c(t), t)) - t**5*x_f*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5 + 10*t**3*x_f*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/(t_f**5*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)) + x_c(t))
-K_t*(T_t*(Derivative(l(t), t) - (50*t**6*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)*(1120*t**3/t_f**4 + 6*t**2*(56*t/t_f**2 - 63/t_f)/t_f**2 - 3780*t**2/t_f**3 + 10*t*(168*t**2/t_f**3 - 378*t/t_f**2 + 216/t_f)/t_f + 12*t*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 4320*t/t_f**2 + 10*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 1680/t_f)/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + 50*t**6*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(-2*t**5*(-l_0 + l_f)*(280*t**3/t_f**4 - 945*t**2/t_f**3 + 1080*t/t_f**2 - 420/t_f)/t_f**5 - 10*t**4*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)**2/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + 50*t**6*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2*(-20*t**3*(l_0 - l_f)*(560*t**3/t_f**4 + 3*t**2*(56*t/t_f**2 - 63/t_f)/t_f**2 - 1890*t**2/t_f**3 + 5*t*(168*t**2/t_f**3 - 378*t/t_f**2 + 216/t_f)/t_f + 6*t*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 2160*t/t_f**2 + 5*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840/t_f)/t_f**5 - 60*t**2*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)**2/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**3) + 300*t**5*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)**2/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + (-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)*(-2*t**5*(-l_0 + l_f)*(280*t**3/t_f**4 - 945*t**2/t_f**3 + 1080*t/t_f**2 - 420/t_f)/t_f**5 - 10*t**4*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)/2)/sqrt(100*t**6*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)**2/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + (-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2)) - sqrt(100*t**6*x_f**2*(-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)**2/(t_f**10*(-g + 10*t**3*(l_0 - l_f)*(140*t**4/t_f**4 - 630*t**3/t_f**3 + 3*t**2*(28*t**2/t_f**2 - 63*t/t_f + 36)/t_f**2 + 1080*t**2/t_f**2 + 5*t*(56*t**3/t_f**3 - 189*t**2/t_f**2 + 216*t/t_f - 84)/t_f - 840*t/t_f + 252)/t_f**5)**2) + (-l_0 - t**5*(-l_0 + l_f)*(70*t**4/t_f**4 - 315*t**3/t_f**3 + 540*t**2/t_f**2 - 420*t/t_f + 126)/t_f**5)**2) + l(t)) - g





Text(0.5, 1.0, 'Longueur')

[0. 0. 0. 0. 0. 0.]





Text(0.5, 1.0, 'longueur $l(t)$')

\(\displaystyle \left( -0.234930948158735, \ 4.30557876347815, \ -3.15, \ 0.15\right)\)

7.2.6. Evitement d’un obstacle (optionnel)

• au milieu de la trajectoire se trouve un obstacle et la charge doit avoir en ce point une hauteur \(l_m\).

• Refaire la planification de trajectoire dans ce cas: trajectoire ACB

• sans obstacle la trajectoire droite: $\( y = l_0 + (l_f-l_0) x \)$

• avec obstacle tq \(y=y_a\): on xie par une parabole $\( y = l_0 + (l_f-l_0) x (a+bx+cx^2)\)$

avec 3 conditions:

• \(y = l_f\) en x=1

• \(y = l_a\) en x=1/2

• \(\dot{y} = 0\) en x=1/2

pour \(l_a = 2l_f - l_0\) on trouve:

\[ y = l_0 + (l_f-l_0) x (9-12x+4x^2)\]

7.2.7. FIN du TP