TP OUTPUT célérité d’un choc par machine learning

7.7. TP OUTPUT célérité d’un choc par machine learning#

Marc BUFFAT, dpt mécanique, UCB Lyon 1

tube a choc

modèle

7.7.1. Principe du machine learning#

problème : prédire une loi \(\mathcal{F}\)

\[ Y = \mathcal{F}(\textbf{X}) \]

à partir de l’apprentissage à l’aide d’une base de données de test \(\textbf{X}_i, Y_i\)

\(\rightarrow\) Problème de minimisation

Trouver la meilleur approximation \(\mathbf{F}\) minimisant l’erreur \(J\) sur la base de données d’apprentissage. \(J\) est une fonction coût du type:

\[ J = \sum_i \alpha_i || \mathbf{F}(\mathbf{X}_i) - Y_i ||^2 \]

  • \(\mathbf{F}(\mathbf{X}_i)\) est fonction d’une combinaison linéaire des données $\(\mathbf{F}(\mathbf{X}_i) = \mathbf{F}\left(\sum_j \beta_j \mathbf{X}_{i,j}\right)\)$

  • pas de forme explicite pour \(\mathbf{F}\) qui dépend de très nombreux paramètres à déterminer par une méthode de minimisation (de type gradient)

  • aucune méthode universelle

\(\rightarrow\) Algorithme implicite nécessitant des données annotées (i.e. avec le résultat) pour l’apprentissage et les tests de validation (apprentissage supervisée)

7.7.2. Lecture de la base de données expérimentales#

  • conditions expérimentales \(p_1\), \(\rho_1\), \(p_2\), \(\rho_2\)

  • mesures (célérité)

  • choc ss

  • contacte cs

  • détentes efts efhs

png

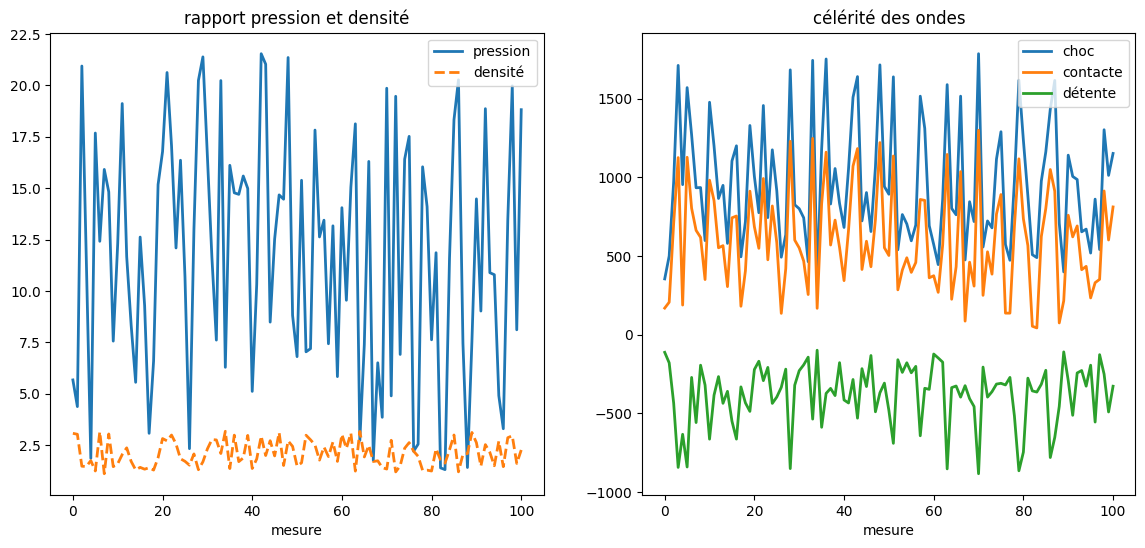
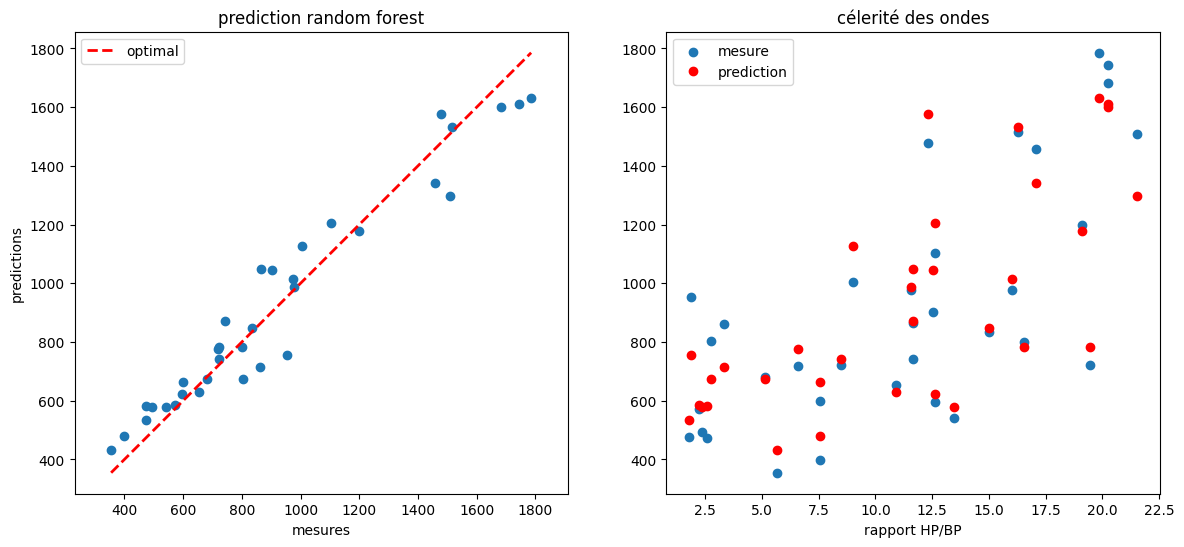
7.7.3. Apprentissage sur les données brutes#

création des tableaux X (données) y (résultats) puis split en training et test

taille des données: (101, 4) (101,)
entrainement / test: (67, 4) (34, 4)


score apprentissage = 98%
R2 score (prediction) = 0.94

png

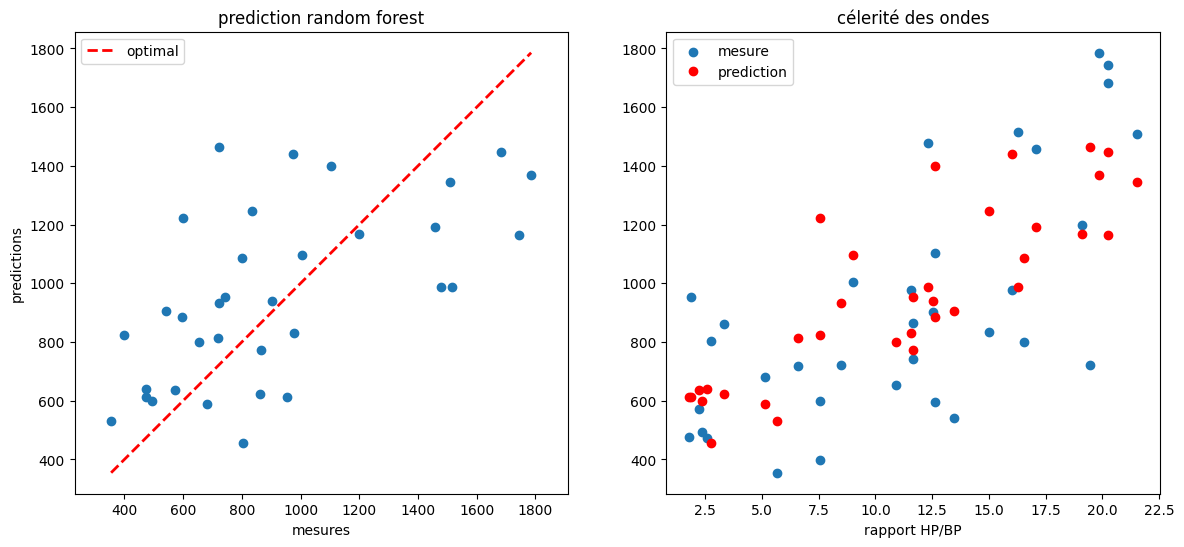
7.7.4. apprentissage / au rapport de pression et densité#

taille des données: (101, 2) (101,)
entrainement / test: (67, 2) (34, 2)


score apprentissage = 85%
R2 score (prediction) = 0.33

png

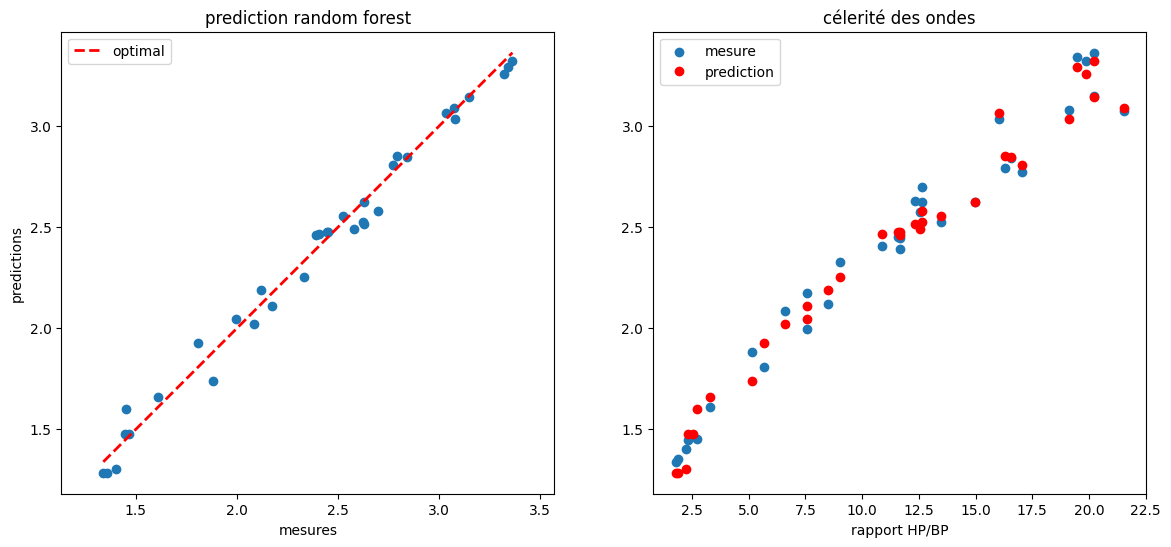
7.7.5. apprentissage sur les données sans dimension#

taille des données: (101, 2) (101,)
entrainement / test: (67, 2) (34, 2)


score apprentissage = 99%
R2 score (prediction) = 0.99

png

7.7.6. Questions#

  • dépendance aux données

  • apport du machine learning

  • intelligence artificiel ?

  • modèle explicatif ?

7.7.7. FIN#

Python version: 3.10.12
numpy version: 1.23.4
skit learn version: 1.1.3
Contenu