7. Programmation objet en Python#
Marc BUFFAT , Université Claude Bernard Lyon 1
%matplotlib inline
# option de mise en page
from IPython.display import HTML,display,IFrame
# bibliotheques de base
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
7.1. Paradigme de programmation#
7.1.1. programmation procédurale (impérative)#
la méthode la plus ancienne (et la plus simple)
on écrit des procédures (fonctions) pour traiter les données (argument)
analyse descendante (on découpe le problème en sous-problèmes plus simples)
programmation ascendante: écriture de procédure (fonction) pour chaque sous-problèmes
7.1.2. programmation oriénté objet#
basée sur la définition d’objets : données + méthodes
objet
données (ou attributs) caractéristiques de l’objet
méthodes (ou fonctions) qui manipulent ces données et gérent les interactions
classe
c’est une structure qui va permettre de définir un objet
extension de la notion de type
notation
soit un objet O de la classe C, dans lequel on définit une donnée x et une méthode func
O = C(args….) création objet
O.x accés aux données
O.func(args…) appel de la fonction remarque l’appel d’une méthode O.func(args..) est en fait interpréter comme C.func(O,args..)
On passe l’objet comme premier argument à la méthode
pointeur Un pointeur est en programmation une variable contenant une adresse mémoire. Cela permet de faire de l’adressage indirecte et de manipuler des données complexes.
la POO utilise (en la cachant) des pointeurs (en particulier vers les méthodes)
7.1.3. Variables#
variables simples
tableau, liste
attention aliasing
IFrame("https://pythontutor.com/iframe-embed.html#code=%23%20variables%20simples%0Ax%20%3D%202%0Ay%20%3D%20x%0Ax%20%3D%203%0A%23%20variables%20complexes%20%28tableaux%20listes%29%0AX%3D%5B2%5D%0AY%3DX%0AX%5B0%5D%3D3&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=0&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false"
,width=800,height=400)
print("Variable de type scalaire (immutable)")
x=2
y=x
x=3
print("x={} y={} @x={} @y={}".format(x,y,hex(id(x)),hex(id(y))))
Variable de type scalaire (immutable)
x=3 y=2 @x=0x7ff1b2bb8130 @y=0x7ff1b2bb8110
print("Variable de type complexe: liste,tableau,.. (mutable)")
X=[2]
Y=X
X[0]=3
print("x={} y={} @x={} @y={}".format(X,Y,hex(id(X)),hex(id(Y))))
Variable de type complexe: liste,tableau,.. (mutable)
x=[3] y=[3] @x=0x7ff17e9938c0 @y=0x7ff17e9938c0
def fonction(X):
Y = X
return Y
#
a = 2
b = fonction(a)
a = 1
print("a,b=",a,b)
A = [2]
B = fonction(A)
A[0] = 1
print("A,B=",A,B)
a,b= 1 2
A,B= [1] [1]
7.2. Objets en Python#
Python permet les 2 paradigmes de programmation
procédurale
POO
Python est en fait un langage objet (mais sans forcer son utilisation), car tout est objet en Python.
Chaque variable V a des méthodes associées V.methode(..)
7.2.1. exemple: chaine de caractère#
IFrame("https://pythontutor.com/iframe-embed.html#code=def%20fonction%28X%29%3A%0A%20%20%20%20Y%20%3D%20X%0A%20%20%20%20return%20Y%0A%23%0Aa%20%3D%202%0Ab%20%3D%20fonction%28a%29%0Aa%20%3D%201%0AA%20%3D%20%5B2%5D%0AB%20%3D%20fonction%28A%29%0AA%5B0%5D%20%3D%201&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=0&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",width=800,height=400)
S="12 345"
print(S)
print(type(S))
print(S.split())
print(isinstance(S,int))
print(isinstance(S,str))
12 345
<class 'str'>
['12', '345']
False
True
# liste des méthodes : avec tab
S.capitalize?
7.2.2. méthodes / attributs#
x = 2
y = x+1
print(x,y,type(y))
2 3 <class 'int'>
# print appel méthode
y = x.__add__(1)
print(x,y,type(y))
2 3 <class 'int'>
# print appel de la fonction de classe
y = int.__add__(x,1)
print(x,y,type(y))
2 3 <class 'int'>
7.3. Manipulation de polynômes de 2nd degré#
Définition d’une classe permettant la manipulation de polynômes de 2nd degré
définition des données
définition des méthodes
7.3.1. Classe Poly2#
• attributs: 3 coefficients (a,b,c) du polynômes p(x)=ax^{2}+bx+c
• méthodes:
création d’un objet (instantiation)obj=classe(attribut)
methode Poly2.__init__(self,a,b,c) p=Poly2(a,b,c)
affichage
methode Poly2.__str__(self)
calcul discriminant et des racines
methode Poly2.discrimant(self) methode Poly2.racines(self)
calcul de la valeur du polynôme en x
methode Poly2.__call__(self,x)
somme de 2 polynômes
p1+p2 methode Poly2.__add__(self,p2)
multiplication par un reel \(\alpha\)
p*alpha méthode Poly2.__mul__(self,alpha)
7.3.2. Utilisation de la classe Poly2 (bibliothéque)#
from Poly2 import Poly2
p = Poly2(3,2,-1)
print("polynome p:",p)
print("p(2)=",p(2))
print("discriminant:",p.discriminant())
print("racines:",p.racines())
p1=Poly2(1,3,2)
print("polynome p1",p1)
print("polynome p+2p1 : ",p+p1*2)
polynome p: 3x^2 + 2x + -1
p(2)= 15
discriminant: 16
racines: (-1.0, 0.3333333333333333)
polynome p1 1x^2 + 3x + 2
polynome p+2p1 : 5x^2 + 8x + 3
7.3.3. equivalence des appels p(3)#
print(p(3.))
print(p.__call__(3.))
print(Poly2.__call__(p,3.))
32.0
32.0
32.0
7.3.4. Implementation#
bibliothéque Poly2.py
IFrame("https://pythontutor.com/iframe-embed.html#code=class%20Poly2%28%29%3A%0A%20%20%20%20def%20__init__%28self,a,b,c%29%3A%0A%20%20%20%20%20%20%20%20self.A%20%3D%20a%0A%20%20%20%20%20%20%20%20self.B%20%3D%20b%0A%20%20%20%20%20%20%20%20self.C%20%3D%20c%0A%20%20%20%20%20%20%20%20return%0A%23%0AP1%20%3D%20Poly2%281.0,0.,4%29%0AP2%20%3D%20Poly2%28P1.A,P1.B,P1.C%29%0AP3%20%3D%20P1%0A%23&codeDivHeight=400&codeDivWidth=350&cumulative=false&curInstr=0&heapPrimitives=nevernest&origin=opt-frontend.js&py=3&rawInputLstJSON=%5B%5D&textReferences=false",width=800,height=400)
"""
classe de manipulation de polynomes de degre 2
"""
class Poly2(object) :
"""Polynome du second degre."""
def __init__(self,coefa,coefb,coefc) :
"""Construit un polynome a partir des coefficients a,b,c."""
self.a = coefa
self.b = coefb
self.c = coefc
print("fonction __init__:",self)
return
def __str__(self) :
"""Chaine d'affichage du polynome."""
s = "{0.a}x^2 + {0.b}x + {0.c}".format(self)
return s
def discrimant(self):
"""calcul discriminant du polynôme"""
return self.b**2 - 4*self.a*self.c
def __add__(self,p):
"""somme de 2 polynômes"""
return Poly2(self.a+p.a,self.b+p.b,self.c+p.c)
def calcul(self,x) :
"""Calcul du polynome pour valeur x."""
return self.a*x**2 + self.b*x + self.c
def __call__(self,x) :
"""Utilisation du polynome comme une fonction."""
return self.calcul(x)
def plot(self,a,b):
"""tracer du polynome entre a et b"""
X = np.linspace(a,b,100)
Y = self.calcul(X)
plt.plot(X,Y,lw=2)
plt.title(str(self))
7.3.5. utilisation de la bibliothéque#
from Poly2 import Poly2
# somme de polynomes
p1=Poly2(1,0,-1)
p2=Poly2(0,2,1)
p3=p1+p2
print("somme p1+p3",p3)
p3=Poly2.__add__(p1,p2)
print("somme p1+p3",p3)
p3=p1.__add__(p2)
somme p1+p3 1x^2 + 2x + 0
somme p1+p3 1x^2 + 2x + 0
7.4. Manipulation d’objet CAO en 2D#
gestion de formes géomètriques dans le plan
• Points dans le plan
– attributs: coordonnees x,y (ou angle rayon)
– methodes: distance, produit vectoriel ,…
• Polygônes n points
– attributs: liste de n points
– methodes: barycentre, perimetre, surface
– sous-classes polygone
∗ triangle
∗ carre
∗ rectangle
7.4.1. Utilisation#
bibliotheque CAO2D.py
7.4.1.1. classe Point#
import matplotlib.pyplot as plt
import numpy as np
from CAO2D import Point
P1=Point(0,0)
P2=Point(1,1)
P3=Point(0.5,2.0)
P4=Point(2.0,1.0)
print("P1=",P1," P2=",P2)
# liste objet
print("methode de P1",dir(P1))
print("P1 est un point = ",isinstance(P1,Point))
#
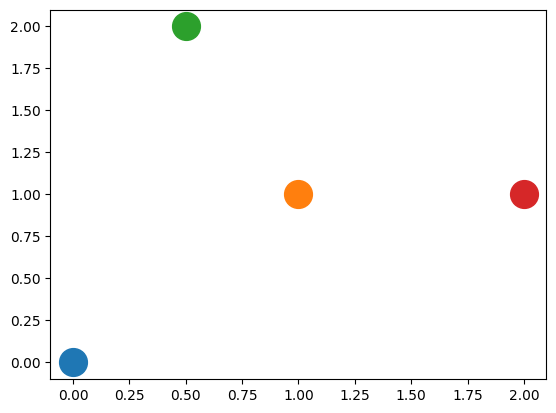
P1.plot()
P2.plot()
P3.plot()
P4.plot()
P1= (0,0) P2= (1,1)
methode de P1 ['__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'plot', 'polaire', 'translation', 'x', 'y']
P1 est un point = True
7.4.1.2. Classe Polygone#
Polygone de n points définit par une liste de points
Triangle = Figure à 3 points
from CAO2D import Polygone, Triangle
#figure
L=[P1,P2,P3,P4]
F=Polygone(L)
print("F=",F)
print("Methode de F :",dir(F))
# Triangle
T=Triangle(P2,P3,P4)
T.translate(1,2)
print("T=",T)
print("Methode de T :",dir(T))
# trace
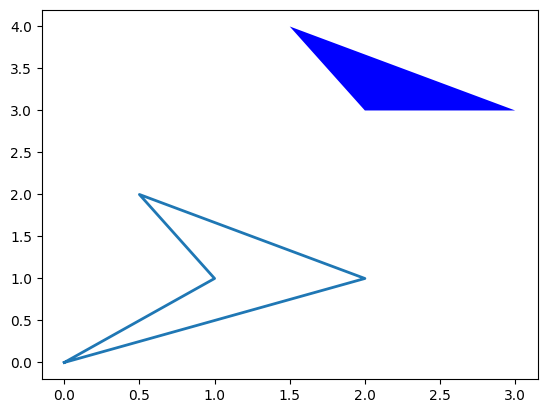
F.plot()
T.plot()
F= figure : (0,0): (1,1): (0.5,2): (2,1)
Methode de F : ['Pts', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'plot', 'translate']
T= figure : (2,3): (1.5,4): (3,3)
Methode de T : ['Pts', '__class__', '__delattr__', '__dict__', '__dir__', '__doc__', '__eq__', '__format__', '__ge__', '__getattribute__', '__gt__', '__hash__', '__init__', '__init_subclass__', '__le__', '__lt__', '__module__', '__ne__', '__new__', '__reduce__', '__reduce_ex__', '__repr__', '__setattr__', '__sizeof__', '__str__', '__subclasshook__', '__weakref__', 'plot', 'translate']
7.4.2. Implementation#
bibliothéque CAO2D.py
7.4.2.1. classe Point#
class Point(object):
def __init__(self,x,y):
"""creation"""
self.x = x
self.y = y
return
def __str__(self):
"""affichage"""
s = "P["+str(self.x)+","+str(self.y)+"]"
return s
def plot(self):
plt.plot([self.x],[self.y],'o')
return
def translation(self,dx,dy):
"""renvoie un pt translater de dx dy"""
return Point(self.x+dx,self.y+dy)
# utilisation
P1=Point(1,2)
P2=Point(0,3)
P3=Point(0,0)
P4=Point(5,0)
print(P1,P2,P3,P4)
P[1,2] P[0,3] P[0,0] P[5,0]
7.4.2.2. classe Polygone#
class Polygone(object):
def __init__(self,L):
self.Pts = L
return
def __str__(self):
s="Polygone:"+str(len(self.Pts))+" points"
return s
def plot(self):
for P in self.Pts:
P.plot()
for i in range(len(self.Pts)):
P1=self.Pts[i]
if i+1 == len(self.Pts):
P2 = self.Pts[0]
else:
P2=self.Pts[i+1]
plt.plot([P1.x,P2.x],[P1.y,P2.y],'-')
return
def translate(self,dx,dy):
"""translate le polygone de dx,dy"""
for i in range(len(self.Pts)):
self.Pts[i] = self.Pts[i].translation(dx,dy)
return
# utilisation
poly1 = Polygone([P1,P2,P3,P4])
print(poly1)
for P in poly1.Pts:
print(P)
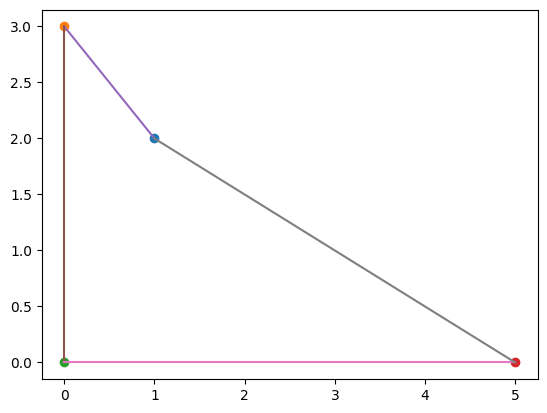
poly1.plot()
Polygone:4 points
P[1,2]
P[0,3]
P[0,0]
P[5,0]
7.4.2.3. sous classe Triangle#
class Triangle(Polygone):
def __init__(self,A,B,C):
self.Pts = [A,B,C]
def plot(self,couleur='c'):
X = [self.Pts[0].x,self.Pts[1].x,self.Pts[2].x]
Y = [self.Pts[i].y for i in range(3)]
Y = [P.y for P in self.Pts]
plt.fill(X,Y,couleur)
# utilisation
T1=Triangle(P1,P2,P3)
T2=Triangle(P2,P4,P1)
T2.translate(1,0)
print(T1)
print(T2)
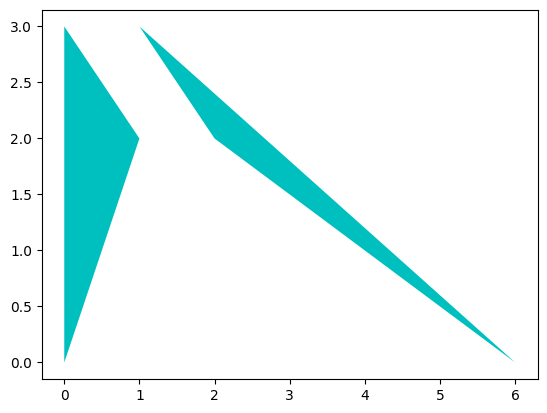
T1.plot()
T2.plot()
Polygone:3 points
Polygone:3 points
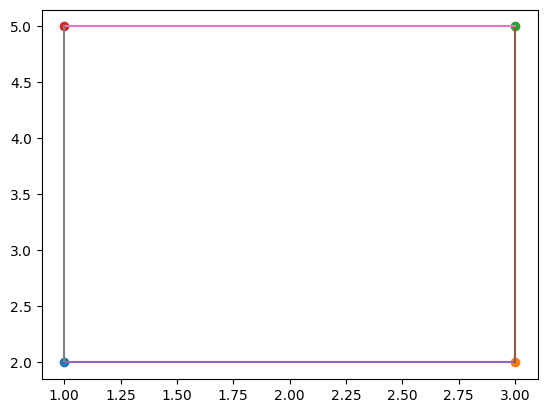
7.4.2.4. sous classe Rectangle#
un point P et 2 longueurs l,H
class Rectangle(Polygone):
def __init__(self,P1,L,H):
P2=P1.translation(L,0)
P3=P1.translation(L,H)
P4=P1.translation(0,H)
self.Pts=[P1,P2,P3,P4]
return
R1=Rectangle(P1,2.,3.)
print(R1)
R1.plot()
Polygone:4 points
7.5. TP programmation Objet CAO 2D#
Objectif du tp
On se propose d’écrire des fonctions Python pour manipuler des éléments en 2D (point, triangle, rectangle, polygones, …). Pour cela on va créer une petite bibliothèque en Python avec des classes.