1. TP reconnaissance de chiffres avec scikit-learn#
Marc Buffat, Dpt Mécanique, UCB Lyon 1
from Python Machine Learning Tutorial
%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt
# police des titres
plt.rc('font', family='serif', size='18')
from IPython.display import display,Markdown
import sklearn as sk
from validation.validation import info_etudiant
def printmd(string):
display(Markdown(string))
# test si numero étudiant spécifier
try: NUMERO_ETUDIANT
except NameError: NUMERO_ETUDIANT = None
if type(NUMERO_ETUDIANT) is not int :
printmd("**ERREUR:** numéro d'étudiant non spécifié!!!")
NOM,PRENOM,NUMERO_ETUDIANT=info_etudiant()
#raise AssertionError("NUMERO_ETUDIANT non défini")
# parametres spécifiques
_uid_ = NUMERO_ETUDIANT
np.random.seed(_uid_)
printmd("**Login étudiant {} {} uid={}**".format(NOM,PRENOM,_uid_))
ERREUR: numéro d’étudiant non spécifié!!!
Login étudiant Marc BUFFAT uid=137764122
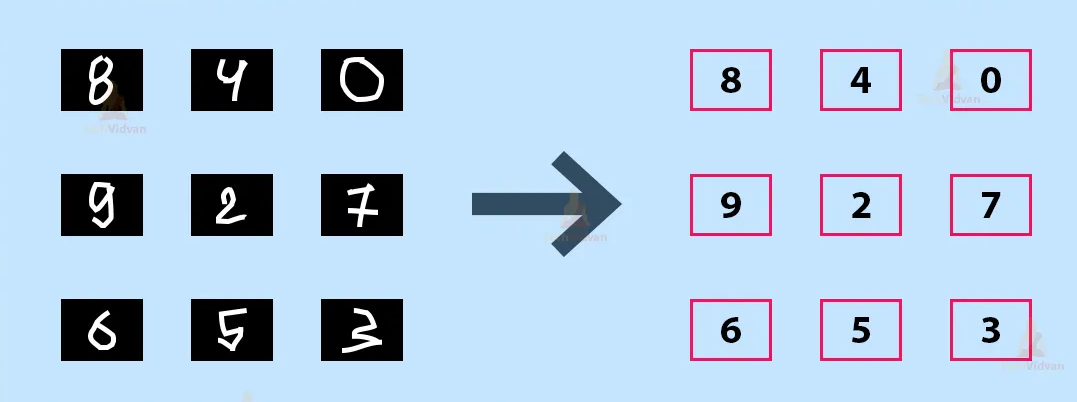
1.1. Principe reconnaissance d’images par IA#
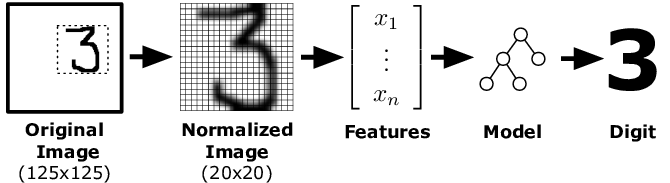
1.2. Base de données de chiffres manuscrits#
Une version basse résolution de cette base de données est fourni avec scikit-learn.
On commence par charger l’échantillon :
from sklearn import datasets
digits = datasets.load_digits()
# information sur la base de données : dataset
display(Markdown(digits.DESCR))
.. _digits_dataset:
Optical recognition of handwritten digits dataset
Data Set Characteristics:
:Number of Instances: 1797
:Number of Attributes: 64
:Attribute Information: 8x8 image of integer pixels in the range 0..16.
:Missing Attribute Values: None
:Creator: E. Alpaydin (alpaydin '@' boun.edu.tr)
:Date: July; 1998
This is a copy of the test set of the UCI ML hand-written digits datasets https://archive.ics.uci.edu/ml/datasets/Optical+Recognition+of+Handwritten+Digits
The data set contains images of hand-written digits: 10 classes where each class refers to a digit.
Preprocessing programs made available by NIST were used to extract normalized bitmaps of handwritten digits from a preprinted form. From a total of 43 people, 30 contributed to the training set and different 13 to the test set. 32x32 bitmaps are divided into nonoverlapping blocks of 4x4 and the number of on pixels are counted in each block. This generates an input matrix of 8x8 where each element is an integer in the range 0..16. This reduces dimensionality and gives invariance to small distortions.
For info on NIST preprocessing routines, see M. D. Garris, J. L. Blue, G. T. Candela, D. L. Dimmick, J. Geist, P. J. Grother, S. A. Janet, and C. L. Wilson, NIST Form-Based Handprint Recognition System, NISTIR 5469, 1994.
.. topic:: References
C. Kaynak (1995) Methods of Combining Multiple Classifiers and Their Applications to Handwritten Digit Recognition, MSc Thesis, Institute of Graduate Studies in Science and Engineering, Bogazici University.
E. Alpaydin, C. Kaynak (1998) Cascading Classifiers, Kybernetika.
Ken Tang and Ponnuthurai N. Suganthan and Xi Yao and A. Kai Qin. Linear dimensionalityreduction using relevance weighted LDA. School of Electrical and Electronic Engineering Nanyang Technological University. 2005.
Claudio Gentile. A New Approximate Maximal Margin Classification Algorithm. NIPS. 2000.
1.2.1. Base de données#
Résultat sous forme de dictionnaire généralisé: Bunch (accès avec des clés aux données)
exploration de la base de données
data (feature) : images de chiffres manuscrits
résultats (target) : valeur numérique 0,1,2,..9
les images de l’échantillon sont des images de 8x8 pixels, en noir et blanc avec 16 niveaux de gris (de 0 à 15) (i.e. codé sur 4 bits).
print(type(digits))
print("clés:",digits.keys())
<class 'sklearn.utils._bunch.Bunch'>
clés: dict_keys(['data', 'target', 'frame', 'feature_names', 'target_names', 'images', 'DESCR'])
Afficher dans la cellule suivante la valeur de la première donnée (data) et du premier résultat (target).
1.2.2. Affichage des images#
affichage d’une image avec imshow
affichage d’une série de nmax images avec la fonction
plot_data
plt.imshow(digits.images[0],cmap='binary')
plt.title(digits.target[0])
plt.axis('off')
plt.show()
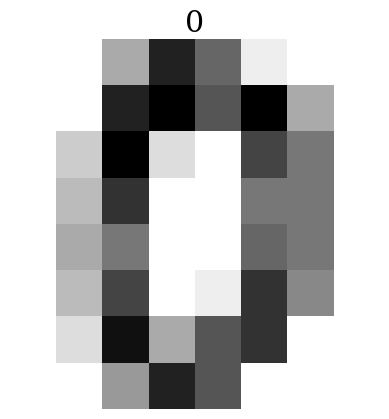
def plot_data(data,target,pred=None,nmax=64,titre=None):
'''affiche les 64 premiers elts de la BD'''
# set up the figure
fig = plt.figure(figsize=(12, 12)) # figure size
if titre is not None: plt.title(titre)
fig.subplots_adjust(left=0, right=1, bottom=0, top=1, hspace=0.05, wspace=0.05)
# plot the digits: each image is 8x8 pixels
for i in range(nmax):
ax = fig.add_subplot(8, 8, i + 1, xticks=[], yticks=[])
image = data[i].reshape(8,8)
ax.imshow(image, cmap=plt.cm.binary, interpolation='nearest')
# label the image with the target value
ax.text(0, 7, str(target[i]),color='b')
# and the predicted value
if pred is not None: ax.text(7,7, str(pred[i]),color='r')
plot_data(digits.data,digits.target,titre="data set initial")

1.3. Création des datasets pour l’apprentissage#
data set d’apprentissage (learn)
data set de validation (test)
décomposition des données: 80% training et 20% test avec un choix aléatoire (fct numéro étudiant)
from sklearn.model_selection import train_test_split
res = train_test_split(digits.data, digits.target,
train_size=0.8,
test_size=0.2,
random_state=NUMERO_ETUDIANT)
train_data, test_data, train_labels, test_labels = res
print("dataset training:",train_data.shape)
print("dataset test :",test_data.shape)
dataset training: (1437, 64)
dataset test : (360, 64)
plot_data(train_data, train_labels,titre="data set d'entrainement")

plot_data(test_data, test_labels,titre="data set de test")

1.3.1. définition des données#
définir les données normalisées (tableaux numpy)
X_train, y_train
X_test, y_test
attention à l’aliasing (utilisation de copy)
# normalisation des donnees
X_train = None
y_train = None
X_test = None
y_test = None
### BEGIN SOLUTION
X_train = train_data/15.0
y_train = train_labels.copy()
X_test = test_data/15.0
y_test = test_labels.copy()
### END SOLUTION
1.4. Modèle linéaire de regréssion logistique#
Création d’un modèle linéaire
scikit learn linear_model
modèle: LogisticRegression
La régression logistique, malgré son nom, est un modèle linéaire de classification plutôt que de régression. La régression logistique est également connue dans la littérature sous le nom de « logit régression », de « classification à entropie maximale » (MaxEnt) ou de « classificateur log-linéaire ». Dans ce modèle, les probabilités décrivant les résultats possibles d’un seul essai sont modélisées à l’aide d’une fonction logistique.
La régression logistique est implémentée dans LogisticRegression. Cette implémentation peut s’adapter à une régression logistique binaire, One-vs-Rest ou multinomiale avec régularisation facultative (l1, l2, elasticnet, aucune)
1.4.1. Régression logistique#
La régression logistique est une méthode statistique de prédiction des classes binaires. Le résultat ou la variable cible est de nature dichotomique. Dichotomique signifie qu’il n’y a que deux classes possibles. Il calcule la probabilité d’occurrence d’un événement.
Il s’agit d’un cas particulier de régression linéaire où la variable cible est de nature catégorielle. Il utilise un journal des cotes comme variable dépendante. La régression logistique prédit la probabilité d’occurrence d’un événement binaire à l’aide d’une fonction logit.
Equation linéaire de régression
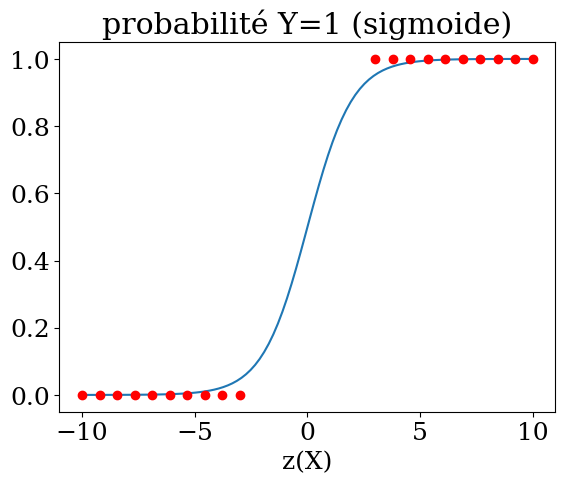
Fonction sigmoide $\( p = \frac{1}{1+e^{-z}} \)$
probalité y=1 $\( p = \frac{1}{1+e^{-(\beta_0 + \beta_1 X_1 + ... + \beta_n X_n)}}\)$
Y = np.linspace(-10,10,100)
plt.title("probabilité Y=1 (sigmoide)")
plt.plot(Y,1./(1+np.exp(-Y)))
Y1 = np.linspace(-10,-3,10)
plt.plot(Y1,np.zeros(10),'or')
plt.plot(-Y1,np.ones(10),'or')
plt.xlabel('z(X)');
Remarque La régularisation est appliquée par défaut, ce qui est courant dans le machine learning mais pas dans les statistiques. Un autre avantage de la régularisation est qu’elle améliore la stabilité numérique.
à faire: modifier les paramètres en utilisant la documentation
paramétres
max_iter (de 100 à 200)
normalisation des données
régularisation
Dans les 2 cellules suivantes faire
l’apprentissage du modèle avec son score
le test du modèle et l’analyse de la qualité de la prédiction (critère accuracy_score, r2_score)
on calulera y_pred et accuracy (taux de prediction)
import sklearn.linear_model
model=None
### BEGIN SOLUTION
model = sklearn.linear_model.LogisticRegression(penalty='l2',max_iter=200)
model = model.fit(X_train,y_train)
### END SOLUTION
from sklearn.metrics import accuracy_score,r2_score
y_pred = None
accuracy = None
### BEGIN SOLUTION
y_pred=model.predict(X_test)
print("predictions:\n",y_pred)
accuracy=accuracy_score(y_pred,y_test)
print("taux de prediction {:3d}%".format(int(accuracy*100)))
print("R2 score {:.2f}".format(r2_score(y_test, y_pred)))
### END SOLUTION
predictions:
[7 3 6 3 7 5 0 5 0 7 8 4 6 1 1 2 8 5 6 5 9 3 9 2 0 1 5 5 3 4 0 3 2 0 9 5 0
4 6 0 6 7 7 2 0 7 8 7 7 9 6 5 5 4 2 2 4 7 3 5 1 1 6 5 6 1 0 9 1 5 1 9 0 6
5 4 8 1 5 8 4 9 6 1 7 1 7 6 5 7 5 3 8 2 0 5 9 0 2 1 1 1 0 9 4 0 5 5 3 1 0
6 8 6 5 2 7 6 1 6 8 0 3 8 3 6 5 3 8 2 3 6 9 6 8 2 3 1 9 3 9 5 5 9 8 1 4 7
4 6 2 2 7 6 2 8 7 9 3 4 8 9 6 9 9 7 6 6 4 3 3 3 4 3 8 4 9 9 1 7 0 8 0 4 2
8 6 8 9 8 5 8 9 8 3 4 7 1 7 2 3 1 7 7 6 2 0 7 3 2 0 5 0 6 0 6 3 6 5 3 4 8
4 0 4 4 8 5 3 8 1 6 9 8 8 2 8 7 8 0 1 6 0 4 7 6 5 1 6 0 2 7 5 3 2 3 7 5 8
1 8 4 7 2 2 1 8 1 9 0 2 0 3 0 3 2 5 9 8 4 3 6 1 7 0 5 6 8 3 3 5 4 9 4 1 6
5 6 0 5 8 6 1 9 9 8 9 5 9 4 8 9 8 3 0 2 9 7 3 3 4 3 4 4 3 8 9 2 0 5 2 9 7
0 5 6 6 0 6 3 5 2 9 6 5 5 1 0 4 2 7 2 3 1 5 5 8 5 7 1]
taux de prediction 97%
R2 score 0.92
1.4.2. Bonus#
visualiser les échantillons où le modèle s’est trompé de beaucoup
conclusion
# test erreur
## BEGIN SOLUTION
print("Erreur:\n",y_test==y_pred)
## END SOLUTION
Erreur:
[ True True True True True True True True True True True True
True True True True True True True False False True True True
True True False True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True False True True
True True True True True True True True True True True True
True True True True False True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True False True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True False True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True True True True True True True True
True True True True True False True True True True True True
True True True True True True True True True True True True]
1.5. Optionnel (test avec modèle random forest, SVM)#
1.5.1. Test du modèle Random Forest#
A faire: modifier les paramètres de RandomForestClassifier pour améliorer le score.
Il est au moins possible d’arriver à 97% en changeant juste les valeurs de n_estimators et max_features. La documentation est disponible à cette adresse :
Dans les 2 cellules suivantes faire
l’apprentissage du modèle avec son score
le test du modèle et l’analyse de la qualité de la prédiction (critère accuracy_score, r2_score)
on calulera y_pred et accuracy (taux de prediction)
from sklearn.ensemble import RandomForestClassifier
model=None
### BEGIN SOLUTION
model = RandomForestClassifier(n_estimators=7,verbose=1,max_features=10)
model = model.fit(X_train,y_train)
### END SOLUTION
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 7 out of 7 | elapsed: 0.0s finished
y_pred = None
accuracy = None
### BEGIN SOLUTION
y_pred=model.predict(X_test)
print("predictions:\n",y_pred)
accuracy=accuracy_score(y_pred,y_test)
print("taux de prediction {:3d}%".format(int(accuracy*100)))
print("R2 score {:.2f}".format(r2_score(y_test, y_pred)))
### END SOLUTION
predictions:
[7 3 6 3 7 5 0 5 0 7 8 4 6 1 1 2 8 5 6 3 1 3 9 2 0 1 8 5 3 4 0 3 2 0 9 5 0
4 6 0 6 7 7 2 0 7 1 7 7 9 6 5 5 4 2 2 4 7 3 5 1 1 6 5 6 1 0 9 1 5 1 9 0 6
5 4 8 1 5 8 4 1 6 1 7 1 7 6 5 7 5 3 3 2 0 5 9 0 2 1 1 1 0 9 4 0 5 5 3 1 0
6 8 6 5 2 7 6 1 6 8 0 3 8 3 6 5 3 1 2 3 6 9 6 8 2 3 1 9 3 9 5 5 7 8 1 4 7
9 6 2 2 7 6 2 8 7 9 3 4 7 9 5 9 9 7 6 6 4 3 3 3 4 3 8 4 9 9 1 7 0 8 0 4 2
2 6 8 9 9 5 8 7 8 3 4 7 1 7 2 3 1 7 7 1 2 0 7 3 2 0 5 0 6 0 6 3 6 5 3 4 9
4 0 4 4 8 5 3 8 1 6 9 8 8 2 8 7 8 0 1 6 0 4 7 6 5 1 6 0 2 7 5 3 2 1 7 5 8
1 8 4 7 2 2 1 8 1 9 0 2 0 3 0 3 2 5 9 6 4 3 6 1 7 0 5 6 8 3 3 5 4 9 4 1 6
5 6 0 5 8 6 1 9 9 8 9 5 9 4 8 9 8 3 0 2 7 7 3 3 4 3 4 4 3 8 7 2 0 5 2 9 7
0 5 6 6 0 6 3 5 5 9 6 5 5 1 0 4 2 7 2 3 1 5 5 8 5 7 1]
taux de prediction 95%
R2 score 0.89
[Parallel(n_jobs=1)]: Using backend SequentialBackend with 1 concurrent workers.
[Parallel(n_jobs=1)]: Done 7 out of 7 | elapsed: 0.0s finished
1.5.2. Test modèle: machines à vecteurs de support SVM#
A faire: modifier les paramètres de svm.SVC pour améliorer le score. Il est au moins possible d’arriver à 95%.
La documentation est disponible à cette adresse :
Dans les 2 cellules suivantes faire
l’apprentissage du modèle avec son score
le test du modèle et l’analyse de la qualité de la prédiction (critère accuracy_score, r2_score)
on calulera y_pred et accuracy (taux de prediction)
from sklearn import svm
model=None
### BEGIN SOLUTION
model = svm.SVC(C=1.0, kernel="rbf", degree=3)
model = model.fit(X_train,y_train)
### END SOLUTION
y_pred == None
accuracy = None
### BEGIN SOLUTION
y_pred=model.predict(X_test)
print("predictions:\n",y_pred)
accuracy=accuracy_score(y_pred,y_test)
print("taux de prediction {:3d}%".format(int(accuracy*100)))
print("R2 score {:.2f}".format(r2_score(y_test, y_pred)))
### END SOLUTION
predictions:
[7 3 6 3 7 5 0 5 0 7 8 4 6 1 1 2 8 5 6 5 1 3 9 2 0 1 8 5 3 4 0 3 2 0 9 5 0
4 6 0 6 7 7 2 0 7 8 7 7 9 6 5 5 4 2 2 4 7 3 5 1 1 6 5 6 1 0 9 1 5 1 9 0 6
5 4 8 1 5 8 4 1 6 1 7 1 7 6 5 7 5 3 8 2 0 5 9 0 2 1 1 1 0 9 4 0 5 5 3 1 0
6 8 6 5 2 7 6 1 6 8 0 3 8 3 6 5 3 8 2 3 6 9 6 8 2 3 1 9 3 9 5 5 9 8 1 4 7
4 6 2 2 7 6 2 8 7 9 3 4 7 9 6 9 9 7 6 6 4 3 3 3 4 3 8 4 9 9 1 7 0 8 0 4 2
8 6 8 9 8 5 8 9 8 3 4 7 1 7 2 3 1 7 7 6 2 0 7 3 2 0 5 0 6 0 6 3 6 5 3 4 9
4 0 4 4 8 5 3 8 1 6 9 8 8 2 8 7 8 0 1 6 0 4 7 6 5 1 6 0 2 7 5 3 2 3 7 5 8
1 8 4 7 2 2 1 8 1 9 0 2 0 3 0 3 2 5 9 8 4 3 6 1 7 0 5 6 8 3 3 5 4 9 4 1 6
5 6 0 5 8 6 1 9 9 8 9 5 9 4 8 9 8 3 0 2 9 7 3 3 4 3 4 4 3 8 9 2 0 5 2 9 7
0 5 6 6 0 6 3 5 5 9 6 5 5 1 0 4 2 7 2 3 1 5 5 8 5 7 1]
taux de prediction 98%
R2 score 0.97
1.5.3. Analyse et conclusion#
écrire votre analyse et conclusion en markdown dans la cellule suivante:
