5. Méthodes de minimisation en IA#
Marc Buffat dpt mécanique, université Lyon 1
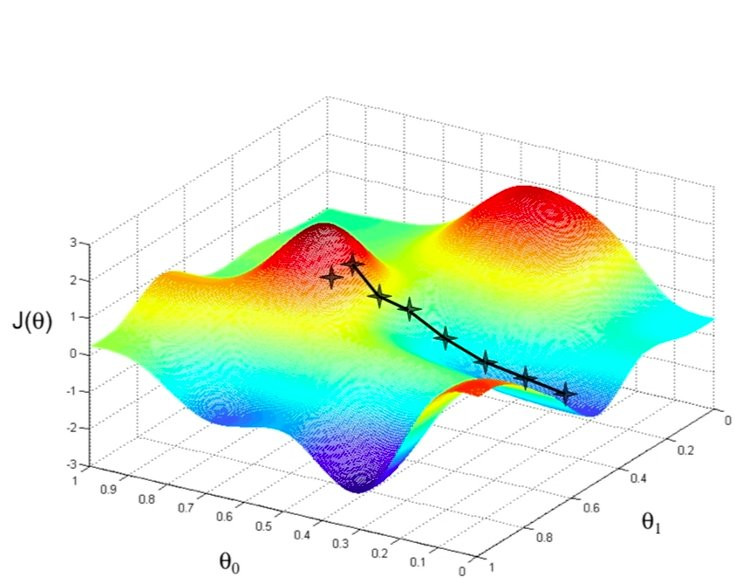
5.1. Introduction#
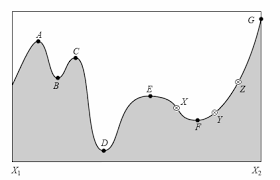
c’est un problème en général mal posé!
Il n’y a pas de méthode idéale
Il est facile de trouver un minimum local
Il est difficile trouver un minimum absolu
Difficultés
Importance de l’approximation initiale
Recherche beaucoup plus difficile si la fonction dépend de plusieurs variables
=> minimisation en N dimensions pour N grand est très difficile
5.2. Algorithme de minimisation (optimisation)#
Pour déterminer la meilleur prédiction, on cherche donc à optimiser (minimiser) une fonction objectif \(J\)
Les algorithmes d’optimisation peuvent être regroupés en 2 groupes: en ceux qui utilisent des dérivés et ceux qui n’en utilisent pas.
Les algorithmes classiques utilisent les dérivéee premières (gradient) et parfois secondes (hessian) de la fonction objectif.
La recherche directe et les algorithmes stochastiques sont conçus pour les fonctions objectifs pour lesquelles les dérivées ne sont pas disponibles.
Les fonctions dérivables simples peuvent être optimisées analytiquement, comme le problème régression linéaire à 2 paramètres réels. Typiquement, l’optimisation des fonctions objectifs qui nous intéressent ne peut pas être résolue analytiquement.
L’optimisation est nettement plus facile si le gradient de la fonction objectif peut être calculé: \(\Rightarrow\) algorithmes plus efficaces.
5.2.1. Algorithmes classiques de minimisation#
Algorithme de type bissection en 1D
Algorithme de type descente locale en dimension N
Algorithme non local en dimension N
Remarque : cette taxonomie est inspirée du livre de 2019 «Algorithms for Optimization».
5.3. Algorithmes de type bissection 1D#
Les algorithmes d’optimisation de type bissection sont destinés aux problèmes d’optimisation avec une variable d’entrée où l’on sait que les optima existent dans une plage spécifique.
ces algorithmes ont capables de naviguer efficacement dans la plage connue et de localiser les optima, bien qu’ils supposent qu’un seul optima est présent (appelé fonctions objectives unimodales).
Certains algorithmes peuvent être utilisés sans informations sur les dérivées si elles ne sont pas disponibles.
Principe de la méthode de dichotomie pour la minimisation
On considère une fonction continue \(f(x)\) sur un intervalle \([a,b]\). On suppose que \(f(x)\) admet un minimum unique sur cet intervalle.
À chaque itération :
On choisit deux points proches du milieu :
\(x_1=m−\delta\) , \(x_2=m+\delta\) , avec \(m=(a+b)/2\)
On compare \(f(x_1)\) et \(f(x_2)\)
Si \(f(x_1) < f(x_2)\) le minimum est à gauche \(\leadsto\) \(b=x_2\)
sinon, le minimum est à droite \(\leadsto\) \(a=x_1\)
On répète jusqu’à ce que \(∣b−a∣\) soit petit (tolérance).
Exemples d’algorithmes:
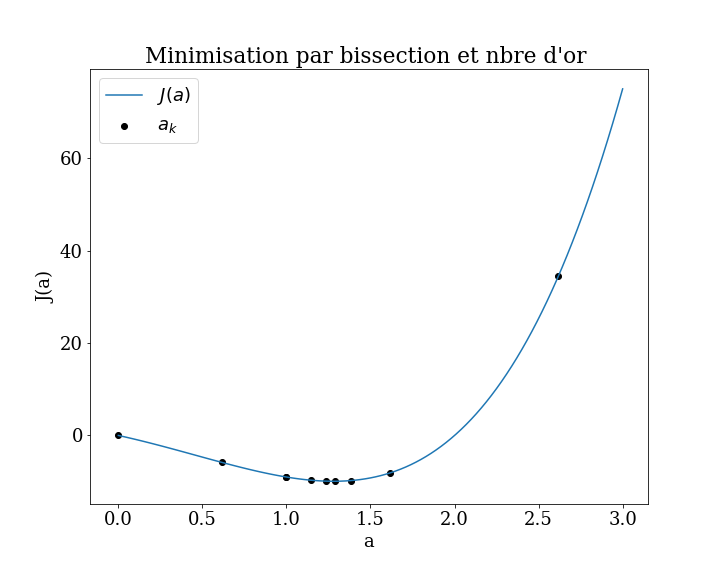
Méthode de bisection (base)
Méthode du nombre d’or (idem mais on remplace 2 par le nombre d’or \(\phi\))
Optimisation de Brent
dans scipy.optimize
scipy.optimize.minimize_scalar
method='brent', 'bounded', 'golden'
Minimization of scalar function of one variable.
5.3.1. scipy.optimize.minimize_scalar#
5.4. Algorithmes de descente locale (dimension N)#
Les algorithmes d’optimisation de descente locale sont destinés aux problèmes d’optimisation avec plus d’une variable d’entrée et un seul optima global (par exemple, une fonction objectif unimodale).
L’exemple le plus courant d’algorithme de descente locale est peut-être l’algorithme line search
line_search \(\mathbf{x}_{k+1}=\mathbf{x}_{k}+\alpha _{k}\mathbf {p} _{k}\).
gradient local (idem avec \( \mathbf{p}_k = -\nabla J\))
gradient conjugué
5.4.1. Line search#
Il existe de nombreuses variantes de cet algorithme (par exemple l’algorithme de Brent-Dekker), mais la procédure consiste généralement à choisir une direction pour se déplacer dans l’espace de recherche, puis à effectuer une recherche de type bissection dans une ligne ou un hyperplan dans la direction choisie.
Algorithme
étape k
calculer une direction de descente \(\mathbf{p}_k\)
Choisir \(\alpha_k\) comme la valeur telle que \(\phi (\alpha )=f(\mathbf{x} _{k}+\alpha \mathbf{p} _{k})\) atteigne son minimum.
Mettre à jour \(\mathbf{x}_{k+1}=\mathbf{x}_{k}+\alpha _{k}\mathbf {p} _{k}\).
itérer si précision non atteinte
Remarques
Ce processus est répété jusqu’à ce qu’aucune autre amélioration ne puisse être apportée.
La limitation est qu’il est coûteux en calcul d’optimiser chaque mouvement directionnel dans l’espace de recherche.
dans scipy.optimize fonction générique minimise
5.4.2. line_search (scipy.optimize.line_search)#
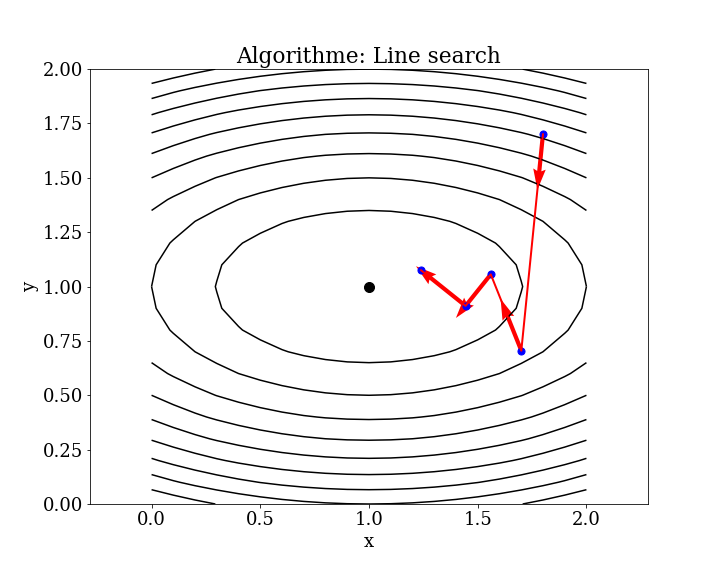
5.4.2.1. méthode de gradient local#
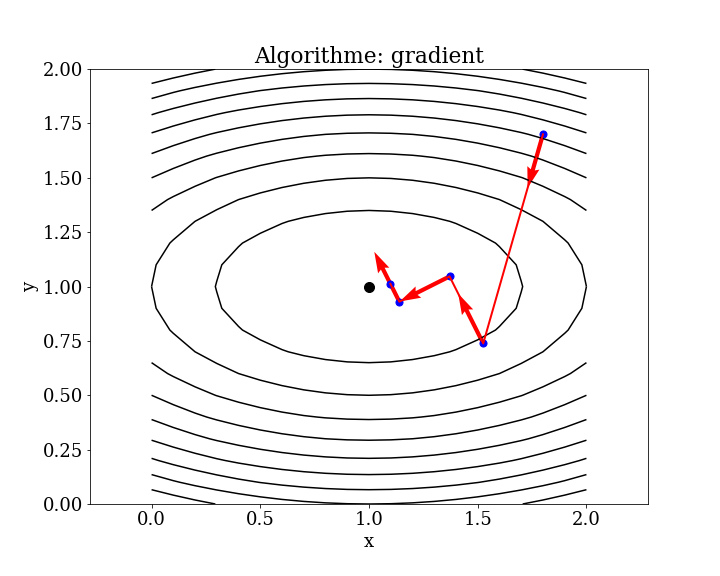
5.4.3. méthode de gradient conjugué local (CG)#
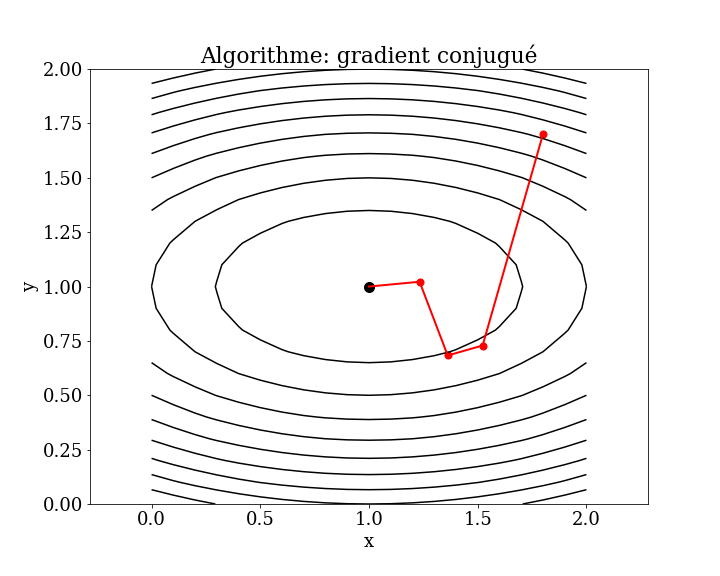
5.5. Algorithmes du premier ordre (généralisation)#
Les algorithmes d’optimisation du premier ordre impliquent explicitement l’utilisation de la dérivée première (gradient) pour choisir la direction à suivre dans l’espace de recherche.
Les procédures consistent d’abord à calculer le gradient de la fonction, puis à suivre le gradient dans la direction opposée (par exemple, descente au minimum pour les problèmes de minimisation) en utilisant une taille de pas (également appelée taux d’apprentissage).
La taille du pas est un hyperparamètre qui contrôle la distance à parcourir dans l’espace de recherche, contrairement aux algorithmes de descente locale qui effectuent une recherche de ligne complète pour chaque mouvement directionnel.
Remarques
Une taille de pas trop petite entraîne une recherche qui prend beaucoup de temps et peut rester bloquée, alors qu’une taille de pas trop grande entraînera des zigzags ou des rebondissements dans l’espace de recherche, manquant complètement les optima.
Les algorithmes de premier ordre sont généralement appelés descente de gradient, avec des noms plus spécifiques faisant référence à des extensions mineures de la procédure.
5.5.1. Algorithme de descente de gradient stochastique (SGD)#
L’algorithme de descente de gradient fournit également le modèle de la version stochastique populaire de l’algorithme, appelée descente de gradient stochastique (SGD), qui est utilisée pour former des modèles de réseaux de neurones artificiels (apprentissage en profondeur).
Cet algorithme est surtout utilisé pour minimiser une fonction coût avec un nombre très important de paramètres. Au lieu de calculer le gradient sur tout le jeu de données, le SGD met à jour les paramètres après chaque exemple (ou petit lot de données). Le paramètre de descente dans la direction du gradient \(\alpha_k\)) est aussi fixé à priori et appelé taux d’apprentissage.
La différence importante est que le gradient est approché plutôt que calculé directement, en utilisant une erreur de prédiction sur les données d’entraînement, comme un échantillon (stochastique), tous les exemples (lot) ou un petit sous-ensemble de données d’entraînement (mini-lot).
Les extensions conçues pour accélérer l’algorithme de descente de gradient (momentum, etc.) peuvent être et sont couramment utilisées avec SGD.
Avantages :
Plus rapide pour les grands jeux de données.
Introduit du bruit aléatoire, ce qui aide à éviter les minima locaux.
Inconvénients :
Les mises à jour sont bruyantes, donc la trajectoire de convergence est moins stable.
Nécessite un bon réglage du taux d’apprentissage.
En résumé :
Le gradient stochastique ajuste les paramètres du modèle petit à petit, à partir d’exemples individuels ou de mini-lots, ce qui rend l’apprentissage plus rapide et plus efficace sur de grandes bases de données.
5.5.2. méthode de gradient stochastique (full batch)#
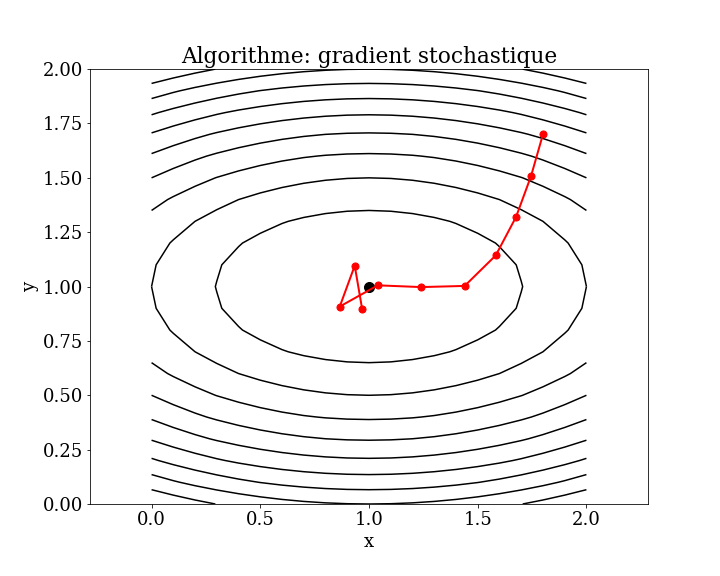
5.5.3. stochastique gradient descent#
A chaque étape de descente de gradient, au lieu de prendre l’ensemble des données, p.e. pour un problème de lissage
initialisation
itération
on itère sur les données une à une:
pour i de 1 à n
5.5.4. Mini-batch#
■ Full batch gradient descent : on calcule le gradient sur l’ensemble du jeu de données
Inconvénient : beaucoup trop long sur un gros jeu de données
■ SGD : on estime le gradient échantillon par échantillon
Inconvénient : lent et convergence plus chaotique
■ Compromis : mini-batch gradient descent
On estime le gradient sur k échantillons à la fois (par exemple 32 échantillons)
5.5.5. Epoch#
■ Dans la SGD, on estime le « gradient » échantillon par échantillon, ou par mini-batches de quelques échantillons
Une passe complète sur le jeu de données s’appelle : une Epoch
■ Le nombre d’épochs est donc le nombre de passes effectuées sur le jeu d’entraînement lors de l’apprentissage.
5.6. Cas de fonction objectif non différentiable#
Les algorithmes d’optimisation qui utilisent la dérivée de la fonction objectif sont rapides et efficaces.
Néanmoins, il existe des fonctions objectives où la dérivée ne peut pas être calculée, généralement parce que la fonction est complexe pour diverses raisons du monde réel. Ou la dérivée peut être calculée dans certaines régions du domaine, mais pas toutes, ou cette dérivée n’est pas un bon guide.
\(\Rightarrow\) difficultés pour ces fonctions objectifs avec les algorithmes classiques
difficultés
Pas de description analytique de la fonction (ex : simulation)
Optima globaux multiples (par exemple fonction multimodale)
Évaluation de la fonction stochastique (par exemple bruitée)
Fonction objectif discontinue (par exemple, régions avec des solutions invalides)
En tant que tels, il existe des algorithmes d’optimisation qui n’utilisent pas les dérivées du premier ou du second ordre.
classification
Ces algorithmes sont parfois appelés algorithmes d’optimisation de type boîte noire car ils supposent peu ou rien (par rapport aux méthodes classiques) sur la fonction objectif.
Ces algorithmes peuvet être classés en :
Algorithme directe (locale)
Algorithme de type stochastique (non local)
Algorithme de type génétique (non local)
5.6.1. Algorithmes directes#
Les algorithmes d’optimisation directe sont destinés aux fonctions objectives pour lesquelles les dérivées ne peuvent pas être calculées.
Les algorithmes sont des procédures déterministes et supposent souvent que la fonction objectif a un seul optimum global, par ex. unimodale.
Les méthodes de recherche directe sont également généralement appelées «recherche de modèle» car elles peuvent naviguer dans l’espace de recherche à l’aide de formes ou de décisions géométriques, par ex. motifs.
Les informations de gradient sont approximées directement (d’où le nom) à partir du résultat de la fonction objectif comparant la différence relative entre les scores pour les points dans l’espace de recherche. Ces estimations directes sont ensuite utilisées pour choisir une direction de déplacement dans l’espace de recherche et trianguler la région des optima.
Exemples d’algorithmes de recherche directe :
Recherche de coordonnées cyclique
Méthode de Powell
Méthode Hooke-Jeeves
Méthode du simplex Nelder-Mead
5.6.1.1. Algorithme du simplex Nelder-Mead#
La méthode de Nelder-Mead est un algorithme d’optimisation non linéaire qui a été publiée par John Nelder et Roger Mead en 1965. C’est une méthode numérique heuristique qui cherche à minimiser une fonction continue dans un espace à plusieurs dimensions.
En algorithmique, une heuristique est une méthode de calcul qui fournit rapidement une solution réalisable, pas nécessairement optimale ou exacte, pour un problème d’optimisation difficile.
simplexe: un simplexe est l’enveloppe convexe d’un ensemble de (n+1) points dans \(\mathcal{R}^n\)
Partant initialement d’un tel simplexe, celui-ci subit des transformations simples au cours des itérations: il se déforme, se déplace et se réduit progressivement jusqu’à ce que ses sommets se rapprochent d’un point où la fonction est localement minimale.
principe en 2D
on part de 3 points qui forment un triangle, et on détermine le point où la fonction est maximum, et on calcul le symétrique / aux 2 autres (réflexion)
si la valeur en ce nouveau point est inférieur à toutes les autres, on construit un simplex avec ce point et on recommence en 1.
si la valeur est meilleure que la seconde mais moins bonne que la meilleur, on remplace la seconde et on recommence en 1.
si la valeur est supérieure à tous les points,le minimum est dans le simplexe initial , on contracte ce simplexe et on recommence en 1.
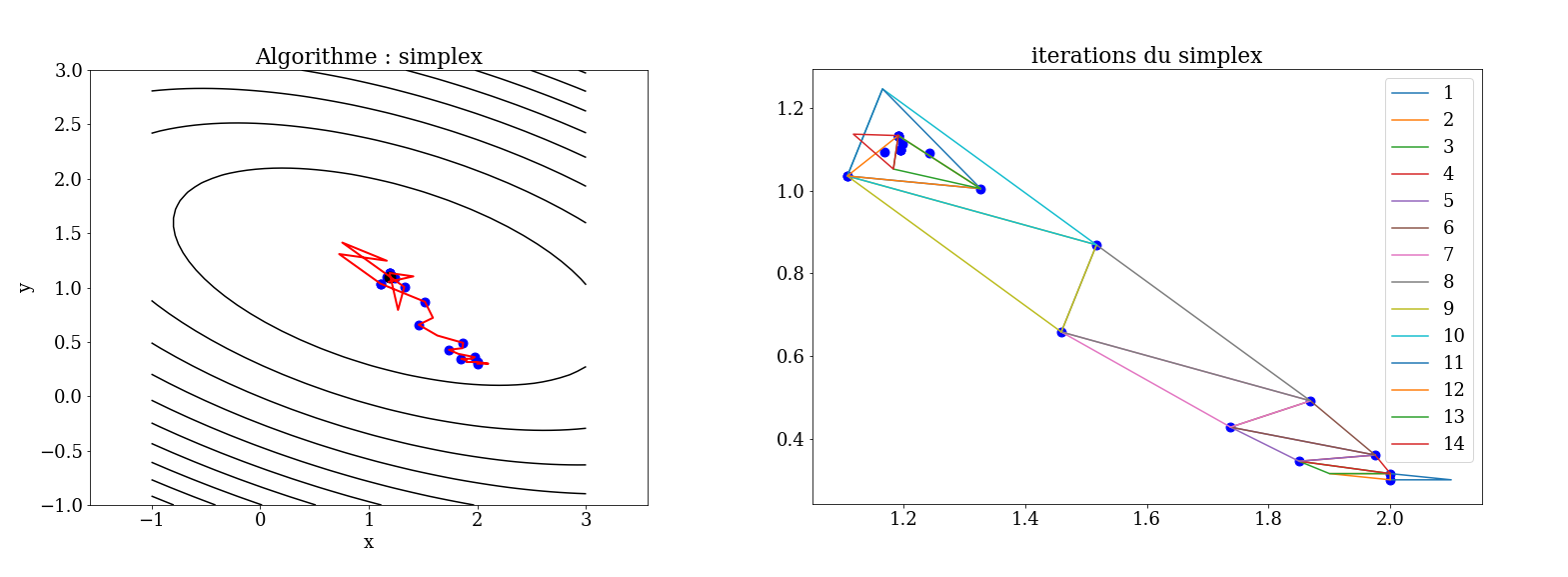
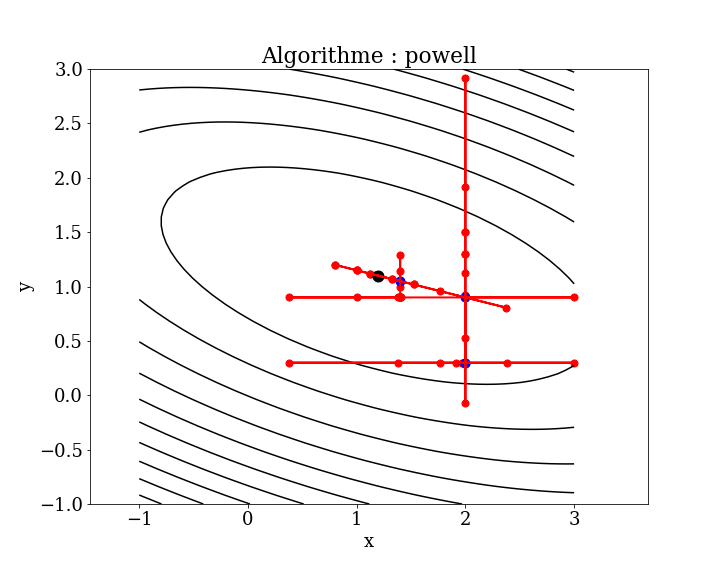
5.6.1.2. Algorithme de Powell#
La méthode minimise la fonction par une recherche de type line search bidirectionnelle. La méthode line search le long de chaque vecteur de recherche peut être effectuée par une dichotomie de type nombre d’or ou la méthode de Brent.
On choisit successivement les directions de descente unitaire suivant chaque coordonnées (paramètre) et on minimise en 1D dans cette direction. $\([x_{0}+\alpha_{1}s_{1},{x}_{0}+\sum_{i=1}^{2}\alpha_{i}{s}_{i},\dots ,{x}_{0}+\sum_{i=1}^{N}\alpha_{i}{s}_{i}]\)\( et on choisit : \)\(x_1 = {x}_{0}+\sum_{i=1}^{N}\alpha_{i}{s}_{i}\)$
puis on itère.
La méthode est utile pour calculer le minimum local d’une fonction continue mais complexe, en particulier une fonction sans définition mathématique sous-jacente, car il n’est pas nécessaire de prendre des dérivées. L’algorithme de base est simple ; la complexité réside dans les recherches linéaires le long des vecteurs de recherche, qui peuvent être réalisées via la méthode de Brent.
5.6.2. Algorithmes stochastiques#
Les algorithmes d’optimisation stochastique sont des algorithmes qui utilisent le caractère aléatoire dans la procédure de recherche de fonctions objectives pour lesquelles les dérivées ne peuvent pas être calculées.
Contrairement aux méthodes de recherche directe déterministes, les algorithmes stochastiques impliquent généralement un échantillonnage beaucoup plus important de la fonction objectif, mais sont capables de gérer les problèmes d’optimums locaux trompeurs.
Les algorithmes d’optimisation stochastique incluent :
Recuit simulé
Stratégie d’évolution
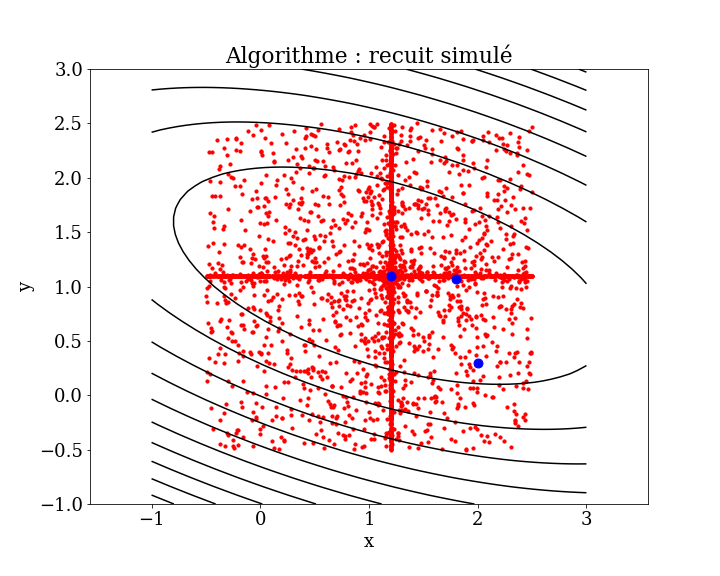
5.6.2.1. Recuit simulé#
Une métaheuristique est un algorithme d’optimisation visant à résoudre des problèmes d’optimisation difficile pour lesquels on ne connaît pas de méthode classique plus efficace.
Les métaheuristiques sont généralement des algorithmes stochastiques itératifs, qui progressent vers un optimum global (c’est-à-dire l’extremum global d’une fonction), par échantillonnage d’une fonction objectif.
Le recuit simulé (méthode empirique (métaheuristique) d’optimisation, inspirée d’un processus utilisé en métallurgie. On alterne des cycles de refroidissement lent et de réchauffage (recuit) pour minimiser l’énergie du matériau. La configuration la plus stable est atteinte en maîtrisant le refroidissement et en le ralentissant par apport de chaleur.
algorithme:
on part de N points pris au hasard et d’une température T élévée
évolution à T constant
on calcule l’énergie \(E\) (erreur) en chacun des points.
on fait évoluer aléatoirement les points (position) ce qui fait varier leur énergie de \(\Delta E\)
si \(\Delta E <0\) on accepte la nouvelle position, sinon elle est acceptée avec une probabilité \(e^{-\Delta E/T}\)
on itère en 3. jusqu’à ce qu’il y ait peu d’évolution (équilibre thermodynamique à T)
on diminue la température T et on recommence en 2
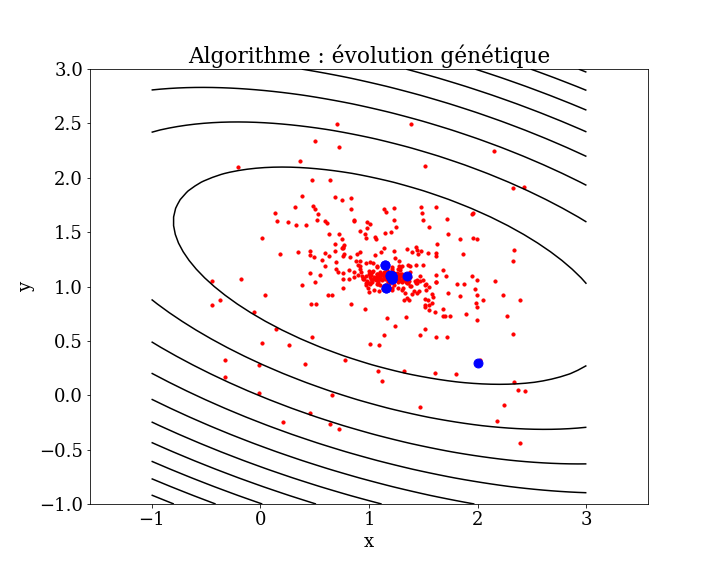
5.6.2.2. Algorithmes génétiques#
Les algorithmes d’optimisation génétiques sont des algorithmes d’optimisation stochastiques qui maintiennent un pool (une population) de solutions candidates qui, ensemble, sont utilisées pour échantillonner, explorer et affiner un optima.
Les algorithmes de ce type sont destinés à des problèmes objectifs plus difficiles qui peuvent avoir des évaluations de fonctions bruitées et de nombreux optima globaux (multimodaux), et trouver une solution bonne ou assez bonne est difficile ou impossible à l’aide d’autres méthodes.
Le pool de solutions candidates ajoute de la robustesse à la recherche, augmentant la probabilité de dépasser les optima locaux.
Voici des exemples d’algorithmes d’optimisation génétique :
Algorithme génétique
Évolution différentielle
5.6.2.3. differential evolution#
l’algorithme d’évolution différentielle est une méthode méta-heuristique stochastique d’optimisation. Elle est inspirée par les algorithmes génétiques et les stratégies évolutionnistes combinées avec une technique géométrique de recherche. Les algorithmes génétiques changent la structure des individus en utilisant la mutation et le croisement, alors que les stratégies évolutionnistes réalisent l’auto-adaptation par une manipulation géométrique des individus.
5.7. Conclusion#
En résumé : Comment s’attaquer à un problème de minimisation:
« Soit à Minimiser la fonction \(F(x_1, ..., x_n)\) à \(N\) variables. »
Le problème est-il bien posé (simple) ?
i.e. idée du minimum, absence de nombreux minima parasites
si oui alors on peut utiliser toutes les méthodes déterministes
si non alors méthodes stocastiques
Si le problème est bien posé (simple) :
Connaissez vous le gradient de F ?
Si oui, vous êtes dans le meilleur cas :
utilisez un méthode de type gradient (gradient conjugué, Fletcher Reeves)
Si non et N=1 :
Utilisez une méthode de type bissection (Brent)
Si non et N>1 :
si F est différentiable, estimation du gradien (méthode de gradient stocastique),
sinon méthode du simplex (Powel)
Si le problème est complexe
Pas d’idée du minimum, nombreux minima parasites etc…
Vous êtes dans le cas le plus difficile.
Tentez une méthode Monte-Carlo telle que recuit-simulé (« Simulated Annealing »)
5.8. Références#
5.8.1. Livres#
« Convex Optimization » Boyd and Vandenberghe, stanford edi.
« Computational Intelligence: An Introduction », 2nd Edition, Andries P. Engelbrecht Wiley 2007
5.8.2. Articles#
« Optimisation mathématique », Wikipédia.
« Algorithmes de minimisation », cours master S. Charnoz, Paris Descarte
5.9. FIN#
Questions ?
