4. Python pour les scientifiques#
Marc BUFFAT, Université Lyon 1
%matplotlib inline
# option de mise en page
from IPython.core.display import HTML,display
# bibliotheques de base
import matplotlib
import numpy as np
import matplotlib.pyplot as plt
from matplotlib import rcParams
rcParams['font.family'] = 'serif'
rcParams['font.size'] = 14
/tmp/ipykernel_3693497/38294169.py:3: DeprecationWarning: Importing display from IPython.core.display is deprecated since IPython 7.14, please import from IPython display
from IPython.core.display import HTML,display
4.1. Questions préliminaires#
plateforme jupyter-exam,
cours MGC2367M (alternant) ou MGC2367MG2 (groupe 2)
4.2. Variables#
# variable entiere, reel, chaine
N=9
print(N,type(N))
X=9.0
print(X,type(X))
S="chaine"
print(S,type(S))
9 <class 'int'>
9.0 <class 'float'>
chaine <class 'str'>
4.2.1. fonction mathématique = bibliotheque numpy renome np#
np.cos, np.sin, np.tan ..
np.log, np.exp, ..
np.asin, np.acos ..
...
aide
np.log?
4.2.2. manipulation de chaine de caractères#
découpage d'une chaine en mots
concaténation de chaine
opérations de recherche et substitution (voir doc)
S="ceci est une chaine"
print("chaine 1:",S)
mots=S.split()
print("mots=",mots)
print("2nd mot=",mots[1])
S2=" pour la suite"
print("chaine 2:",S2)
print("concatenation:",S+S2)
chaine 1: ceci est une chaine
mots= ['ceci', 'est', 'une', 'chaine']
2nd mot= est
chaine 2: pour la suite
concatenation: ceci est une chaine pour la suite
# implementation
4.3. structure de contrôle#
4.3.1. Comparaison#
> , >= , < , <=
== égalité
!= different
True False
and or
print(5 < 4)
print((5 < 4 ) or (3 > 2))
False
True
4.3.2. Test logique if#
example: test si un nombre aléatoire entre -100 et 100 est positif ou negatif
import random
n = random.randint(-100,100)
print("pour n=",n)
if n>0:
print("n positif")
elif n<0:
print("n negatif")
else:
print("n null")
pour n= 98
n positif
# implementation
import random
4.3.3. Boucle for de 0 a N (exclus)#
for i in rang(N):
exp1
exp2
....
4.3.3.1. noter l’utilisation de : et l’indentation dans la boucle#
N=3
print("boucle de 0 a N-1")
for i in range(N):
print(i)
# ou de 1 a N
print("boucle de 1 a N")
for i in range(1,N+1):
print(i)
boucle de 0 a N-1
0
1
2
boucle de 1 a N
1
2
3
# exemple calcul de la somme des N premiers entiers positifs
N=100
S=0
for i in range(1,N+1):
S=S+i
print(S)
5050
# exemple calcul de la somme des N premiers entiers positifs
4.3.4. Exemple : calculer les N=100 premiers termes de la serie S#
\( S_n = x - x^2/2 + x^3/3 + .. \) soit
$\( S_n = - \sum_{i=1}^{N} \frac{(-x)^{i}}{i} \)$
DL de \(log(1+x)\): $\( \lim_{n\rightarrow\infty} S_n = log(1+x) \)$
et tester la convergence (i.e. l’erreur)
# solution
N=100
x=1.0
S=0.0
for i in range(1,N+1):
S = S - (-x)**i/i
print("S100=",S," err=",np.log(1+x)-S)
S100= 0.688172179310195 err= 0.004975001249750255
# implementation
4.3.5. solution optimisee#
# solution optimisee
S=0.0
term=x
for i in range(1,N+1):
S = S + term/i
term = -term*x
print("S100=",S," err=",np.log(1+x)-S)
S100= 0.688172179310195 err= 0.004975001249750255
# implementation
4.3.6. Boucle tant que (while)#
while (condition) :
exp1
exp2
...
4.3.7. Exemple: racine de \(\cos x^2 \) par dichotomie#
algorithme
r = (a+b)/2
tant que abs(cos r^2) > eps
si cos r^2 * cos a^2 > 0 alors
a = r
sinon
b = r
r = (a+b)/2
fin tant que
# solution
def dichotomie(a,b):
r = (a+b)/2.
while np.abs(np.cos(r**2)) > 1.e-1 :
if np.cos(r**2)*np.cos(a**2) > 0:
a = r
else:
b = r
r = (a+b)/2.
print(a,b,r)
#
return r
# implementation sous forme de fonction: dichotomie(a,b)
4.4. validation#
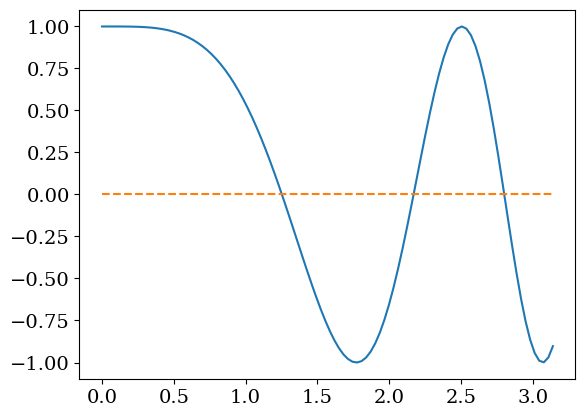
calcul des racines de $\( cos(x^2) = 0 \)$
X=np.linspace(0,np.pi,100)
Y=np.cos(X**2)
plt.plot(X,Y)
plt.plot(X,np.zeros(X.size),'--')
[<matplotlib.lines.Line2D at 0x7eff3420bb50>]
x = dichotomie(0.,1.5)
print(x,np.cos(x**2))
0.75 1.5 1.125
1.125 1.5 1.3125
1.125 1.3125 1.21875
1.21875 0.08534083294179849
4.5. Manipulation de liste#
la liste est un ensemble ordonné de valeurs (eventuelement de type differents)
# liste vide
L=[]
print(L,type(L),"dim=",len(L))
[] <class 'list'> dim= 0
L=[1,'un',2,'deux']
print(L,type(L)," dim=",len(L))
[1, 'un', 2, 'deux'] <class 'list'> dim= 4
# 1er (indice 0) et dernier element (indice -1)
print(L[0],L[1],L[-1])
# extraction d'un sous liste avec un pas de 2
print("sous liste :",L[0:-1:2])
1 un deux
sous liste : [1, 2]
# on peut ajouter (a la fin) ou enlever des elements d'un liste
L.append('quatre')
print(L)
L.remove('quatre')
print(L)
[1, 'un', 2, 'deux', 'quatre']
[1, 'un', 2, 'deux']
4.5.1. Exemple: calcul des nombres premiers inférieurs à N#
algorithme:
boucle sur p de 2 a N
test si p est divisible par un nombre premier précédent
si oui ajouter p a la liste des nombres premiers
on mettra les nombres premiers trouvés dans une liste P
# solution
N=100
P=[2]
for i in range(3,N+1):
premier=True
for p in P:
if i%p == 0 :
premier = False
#print i," n'est pas premier"
break;
if premier:
P.append(i)
#print i, " est premier"
print("liste des nbres premiers <",N,"=",P)
liste des nbres premiers < 100 = [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97]
# implementation
4.5.2. Dictionnaire#
ensemble avec une clé : valeur
dict = { cle: val, ;.}
dict_anglais={'I':'je','a':'un','am':'suis','lonesome':'solitaire'}
dict_anglais['cow-boy']='vacher'
print("dictionaire")
for key,val in dict_anglais.items() :
print(key,'=',val)
phrase='I am a lonesome cow-boy'
print("phrase : ",phrase)
trad=''
for word in phrase.split():
trad=trad+' '+dict_anglais[word]
print("traduction :", trad)
dictionaire
I = je
a = un
am = suis
lonesome = solitaire
cow-boy = vacher
phrase : I am a lonesome cow-boy
traduction : je suis un solitaire vacher
4.5.3. Attention a la copie de structure#
# copie de scalaires
x=1
a=x
a=2
print(a,x)
2 1
# copie de listes
list1 = [[1],[2]]
print("list1=",list1)
list2=list1
list2[0][0]=0
print("list2=",list2)
print("list1=",list1)
list1= [[1], [2]]
list2= [[0], [2]]
list1= [[0], [2]]
4.5.4. Adresse d’une variable et d’une structure#
print("@list1=",hex(id(list1)))
print("@list2=",hex(id(list2)))
print("@list1[0]=",hex(id(list1[0])))
print("@list1[1]=",hex(id(list1[1])))
@list1= 0x7eff342ff480
@list2= 0x7eff342ff480
@list1[0]= 0x7eff342449c0
@list1[1]= 0x7eff342ffa40
4.5.5. Copie versus aliasing#
from copy import deepcopy
list1 = [[1],[2]]
list2 = list1
list3 = deepcopy(list1)
print('@IDs:\nlist1: {}\nlist2: {}\nlist3: {}\n'
.format(hex(id(list1)), hex(id(list2)), hex(id(list3))))
print('list1:', list1)
list2[0][0] = 3
print('list123:', list1,list2,list3)
list3[0][0] = 5
print('list123:', list1,list2,list3)
@IDs:
list1: 0x7eff34a069c0
list2: 0x7eff34a069c0
list3: 0x7eff34a06940
list1: [[1], [2]]
list123: [[3], [2]] [[3], [2]] [[1], [2]]
list123: [[3], [2]] [[3], [2]] [[5], [2]]
4.6. Tableaux numériques numpy#
structure de données optimisée pour manipuler des vecteurs , des matrices ou des n-matrices
création de tableau en spécifiant les dimensions et le type (reel par defaut)
# vecteurs
dim=4
X=np.zeros(dim)
Y=np.ones(dim,dtype=int)
Z=np.random.rand(dim)
print(X)
print(Y)
print(Z)
print("X=",type(X),len(X),X.shape,X.ndim,X.size)
print("Y=",type(Y),len(Y),Y.shape[0])
W=np.linspace(0.,1.,5)
print("W=",W)
[0. 0. 0. 0.]
[1 1 1 1]
[0.88995315 0.91509146 0.14837519 0.62010472]
X= <class 'numpy.ndarray'> 4 (4,) 1 4
Y= <class 'numpy.ndarray'> 4 4
W= [0. 0.25 0.5 0.75 1. ]
# matrices
dim=4
A=np.ones((dim,2*dim))
print(A)
print("A=",type(A),len(A),A.shape,A.ndim,A.size)
[[1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 1. 1.]]
A= <class 'numpy.ndarray'> 4 (4, 8) 2 32
4.6.1. accès aux elements avec un indice commencant à 0#
X[0] 1er element
X[1] 2nd
..
X[-1] dernier
matrice stockage par colonne
A[0,0] 1er element
4.6.2. Exemple: calcul du produit matrice vecteur Y=A.X#
\[Y_i = \sum_{j=1}^M A_{ij} X_j \;\; \forall i=1,N\]
N=3; M=2;
A=np.random.rand(N,M)
print("A=",A)
X=np.ones(M)
print("X=",X)
Y=np.zeros(N)
for i in range(N):
for j in range(M):
Y[i] = Y[i] + A[i,j]*X[j]
print("Y=",Y)
A= [[0.20643148 0.83710686]
[0.68019601 0.83207523]
[0.14239156 0.4388694 ]]
X= [1. 1.]
Y= [1.04353834 1.51227124 0.58126096]
# implementation
4.6.3. Exemple: calcul de la matrice de Vandermonde V (N,M)#
Soit un vecteur \(X\) de dimension \(N\):
\[ V_{ij} = x_i ^{j-1} \;\; \forall i=1,N \;\; \forall j=1,M\]
écrire un algorithme avec des boucles
# implemtation simple
N=5; M=N
X = np.arange(N)
V=np.zeros((N,M))
for i in range(N):
for j in range(M) :
V[i,j] = X[i]**j
print("V=",V)
V= [[ 1. 0. 0. 0. 0.]
[ 1. 1. 1. 1. 1.]
[ 1. 2. 4. 8. 16.]
[ 1. 3. 9. 27. 81.]
[ 1. 4. 16. 64. 256.]]
#implentation simple
# test efficacite
N=200; M=N;
X=np.random.rand(N)
%%timeit -n 4
# version avec des boucles
V=np.zeros((N,M))
for i in range(N):
for j in range(M) :
V[i,j] = X[i]**j
10.1 ms ± 174 μs per loop (mean ± std. dev. of 7 runs, 4 loops each)
%%timeit -n 4
# version optimisee
V1=np.ones((N,M))
for j in range(1,M):
V1[:,j]=V1[:,j-1]*X[:]
427 μs ± 115 μs per loop (mean ± std. dev. of 7 runs, 4 loops each)
4.6.3.1. extraction de sous vecteur ou de sous matrice#
range
[fin]
[deb:fin]
[deb:fin:pas]
[::] equivalent [0:-1:1]
4.6.4. Notation matriciel:#
opérations terme à terme sur les vecteurs et matrices
+ - * / opération terme à terme
N=4
X = np.arange(N)
Y = np.ones(N)
Z = X + Y
print(Z)
Z = X * Y
print(Z)
Z = X / Y
print(Z)
[1. 2. 3. 4.]
[0. 1. 2. 3.]
[0. 1. 2. 3.]
A = np.ones((N,N))
B = A + A
C = B * B
print("A=",A,"\nA+A=",B,"\nB*B=",C)
A= [[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
A+A= [[2. 2. 2. 2.]
[2. 2. 2. 2.]
[2. 2. 2. 2.]
[2. 2. 2. 2.]]
B*B= [[4. 4. 4. 4.]
[4. 4. 4. 4.]
[4. 4. 4. 4.]
[4. 4. 4. 4.]]
4.6.5. produit scalaire, matriciel et tensoriel : fonction numpy dot#
print("X =",X)
print("X*X=",X*X)
print("X.X=",np.dot(X,X))
print("A =",A)
print("A*X=",A*X)
print("A.X=",np.dot(A,X))
X = [0 1 2 3]
X*X= [0 1 4 9]
X.X= 14
A = [[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]
[1. 1. 1. 1.]]
A*X= [[0. 1. 2. 3.]
[0. 1. 2. 3.]
[0. 1. 2. 3.]
[0. 1. 2. 3.]]
A.X= [6. 6. 6. 6.]
4.6.6. resolution systeme lineaire#
bibliotheque linalg de numpy
from numpy.linalg import solve,norm
N=3
A=np.random.rand(N,N)
B=np.ones(N)
X=solve(A,B)
print(X)
err = norm(B-np.dot(A,X))
print("erreur = ",err)
[-2.41029912 1.11895665 1.28468254]
erreur = 0.0
4.6.7. Exemple: polynôme d’interpolation#
Soient N points de mesure \(xk,yk\) calculer les N coefficiants \(a_i\) du polynôme d’interpolation \(p(x)\) de degré \(N-1\) passant par ces \(N\) points.
\[ p(x)=\sum_{i=0}^{N−1} a_i x^i \mbox{ avec } p(x_k)=y_k\]
On notera que les \(a_i\) sont solution du système linéaire: $\( \sum_{j=0}^{N-1} a_j x_i^j = y_i \)$
A.N: \(N=5\) sur \([0,\pi/2]\) pour \(cos(x)\)
N=5
X=np.linspace(0,np.pi/2,N)
Y=np.cos(X)
M=np.ones((N,N))
for j in range(1,N):
M[:,j]=M[:,j-1]*X
A=solve(M,Y)
P=str(A[0])
for j in range(1,N):
P += " + {} x^{}".format(A[j],j)
print("Polynome: ",P)
Polynome: 1.0 + 0.002824120785207486 x^1 + -0.5143253869134662 x^2 + 0.023168662712955968 x^3 + 0.028714225230189197 x^4
# implementation
4.7. Bibliothèques scientifiques Python#
### liste des sous-bibliothèques numpy
random (numpy.random)
algebre lineaire (numpy.linalg)
transforee de Fourier (numpy.fft
matrices (numpy.matlib)
4.7.1. liste des sous-bibliotheques scipy#
Special functions (scipy.special)
Integration (scipy.integrate)
Optimization (scipy.optimize)
Interpolation (scipy.interpolate)
Fourier Transforms (scipy.fftpack)
Signal Processing (scipy.signal)
Linear Algebra (scipy.linalg)
.....
4.8. Fonctions#
fonction implémentation d’un algorithme avec des données (arguments) et un résultat qui est la valeur retournée par la fonction
def nom(arguments) :
""" commentaire """
instruction 1
instruction 2
...
return val
4.8.1. exemple#
écrire une fonction \(f(x)\) calculant \(\frac{\sin{x}}{x}\)
def f(x):
"""calcul de sin(x)/x"""
if abs(x) < 1.e-10:
return 1.
else :
return np.sin(x)/x
print("f(1)=",f(1))
print("f(0)=",f(0))
f(1)= 0.8414709848078965
f(0)= 1.0
# implementation
4.8.2. Exemple: PGCD#
écrire une fonction pgcd qui calcule le PGCD de 2 nombres entiers a et b
algorithme
pgcd(a,b)=pgcd(a,b-a) si a<b
pgcd(a,b)=pgcd(b,a-b) si a>b
pgcd(a,b)=a si a=b
# solution
def PGCD(a,b):
""" calcul PGCD de a et b"""
while a != b :
if a > b :
a = a - b
else:
b = b - a
return a
print("PGCD(9,21)=",PGCD(9,21))
print("PGCD(10,25)=",PGCD(10,25))
PGCD(9,21)= 3
PGCD(10,25)= 5
# implementation
4.8.3. Exemple:#
calculer la valeur en x d’un polynome p(x) donné par ces coefficiants \(a_i\)
\[ p(x) = \sum_i a_i x^i \]
def polynome(x,A):
"""calcul de la valeur en x du polynome sum(a_i*x^i)"""
p=0.0
xi=1
for i in range(A.size):
p += A[i]*xi
xi *= x
return p
P = np.array([0.,0.,1.])
print("Polynome P:",P)
print("P(0)=",polynome(0.,P))
print("P(1)=",polynome(1.,P))
print("P(2)=",polynome(2.,P))
Polynome P: [0. 0. 1.]
P(0)= 0.0
P(1)= 1.0
P(2)= 4.0
# implementation
4.9. Formatage des écritures#
possibilité de formatter les sorties en spécifiant un format (identique a printf en C) avec des champs % (%d entier, %g reels , %s chaine, ..) et des caractères spéciaux (/n suate de ligne, /t tabulation,..)
print "format"%(val1,val2,..)
X=1.0; n=10; S="chaine"
print("X=%g\tn=%d\ntext:\t%s"%(X,n,S))
X=1 n=10
text: chaine
en python 3, on préfere utiliser la fonction format et {}
print("X={:g}\tn={}\ntext:\t{}".format(X,n,S))
X=1 n=10
text: chaine
4.9.1. exemple:#
Afficher la valeur de 2 vecteurs X,Y en affichant pour chaque ligne l’indice (de 1 a N), X[i] et Y[i] séparés par une , (format excel csv)
N=3
X=np.linspace(0,np.pi,N)
Y=np.cos(X)
print("X=",X,"\nY=",Y)
X= [0. 1.57079633 3.14159265]
Y= [ 1.000000e+00 6.123234e-17 -1.000000e+00]
# solution (avec formatage)
for i in range(N):
print("{:2d} , \t{:6.3f} , \t{:6.3f}\n".format(i+1,X[i],Y[i]))
1 , 0.000 , 1.000
2 , 1.571 , 0.000
3 , 3.142 , -1.000
# implementation
4.10. Lecture/écriture des données sur fichier#
fichier = stockage des données sur disque (ou clé USB)
accès avec un nom de fichier et un répertoire (endroit ou est stocké le fichier: peu dépendre du système d’exploitation)
exemple la commande ls sous unix (Linux) affiche la liste des fichiers dans le répertoire courant
%%bash
ls -al donnees*
-rw-rw-r-- 1 buffat buffat 175 mars 19 17:57 donnees.csv
-rw-rw-r-- 1 buffat buffat 505 mars 19 17:57 donnees.dat
-rw-rw-r-- 1 buffat buffat 44 mars 19 17:57 donnees.txt
4.10.1. Manipulation d’un fichier#
1/ ouverture du fichier en spécifiant son nom et le type d'accés (lecture/ecriture)
on récupére une variable F permettant ensuite de manipuler le fichier
2/ pour écrire (write) dans le fichier on formatte les données par ligne
3/ pour lire dans le fichier on lit les données par ligne (readline)
4/ à la fin on foerme le fichier (close)
X=1.0; Y=np.cos(X);
F=open("donnees.txt","w")
print(F)
F.write("# Ceci est un exemple de donnees\n")
F.write("%g %g\n"%(X,Y))
F.close()
<_io.TextIOWrapper name='donnees.txt' mode='w' encoding='UTF-8'>
%%bash
cat donnees.txt
# Ceci est un exemple de donnees
1 0.540302
F=open("donnees.txt",'r')
L=F.readline()
print("1ere ligne: ",L)
L=F.readline()
print("2nd ligne: ",L)
F.close()
1ere ligne: # Ceci est un exemple de donnees
2nd ligne: 1 0.540302
4.10.2. Exemple:#
Ecrire dans un fichier au format csv 2 vecteurs X et Y de dimension N
N=10
X=np.linspace(0,np.pi,N)
Y=np.cos(X)
# correction
F=open("donnees.csv",'w')
for i in range(N):
F.write("%g , %g \n"%(X[i],Y[i]))
F.close()
# implementation
%%bash
cat donnees.csv
0 , 1
0.349066 , 0.939693
0.698132 , 0.766044
1.0472 , 0.5
1.39626 , 0.173648
1.74533 , -0.173648
2.0944 , -0.5
2.44346 , -0.766044
2.79253 , -0.939693
3.14159 , -1
4.10.3. Lecture ecriture de tableaux#
sous numpy
A=loadtxt(nom) lecture tableau A dans le fichier nom
savetxt(nom,X,Y,..)
A=np.loadtxt("donnees.csv",delimiter=",")
X=A[:,0]
Y=A[:,1]
print("X=",X,"\nY=",Y)
X= [0. 0.349066 0.698132 1.0472 1.39626 1.74533 2.0944 2.44346
2.79253 3.14159 ]
Y= [ 1. 0.939693 0.766044 0.5 0.173648 -0.173648 -0.5
-0.766044 -0.939693 -1. ]
np.savetxt("donnees.dat",np.transpose([X,Y]))
4.10.4. Exemple:#
Ecrire dans un fichier la valeur de 3 tableaux de dimension N=4 avec \(X=[0,\pi],Y=cos(X), Z=Y^2sin(X)\) avec par ligne X[i] Y[i] Z[i]
#solution
N=4
X=np.linspace(0,np.pi,N)
Y=np.cos(X)
Z=Y**2 * np.sin(X)
np.savetxt("essai.dat",np.transpose([X,Y,Z]))
print("X=",X,"\nY=",Y,"\nZ=",Z)
print("fichier essai.dat")
!cat essai.dat
X= [0. 1.04719755 2.0943951 3.14159265]
Y= [ 1. 0.5 -0.5 -1. ]
Z= [0.00000000e+00 2.16506351e-01 2.16506351e-01 1.22464680e-16]
fichier essai.dat
0.000000000000000000e+00 1.000000000000000000e+00 0.000000000000000000e+00
1.047197551196597631e+00 5.000000000000001110e-01 2.165063509461097324e-01
2.094395102393195263e+00 -4.999999999999997780e-01 2.165063509461094826e-01
3.141592653589793116e+00 -1.000000000000000000e+00 1.224646799147353207e-16
# implementation
4.11. Tracer de courbe#
bibliotheque matplotlib
import matplotlib.pyplot as plt
visiter le site:
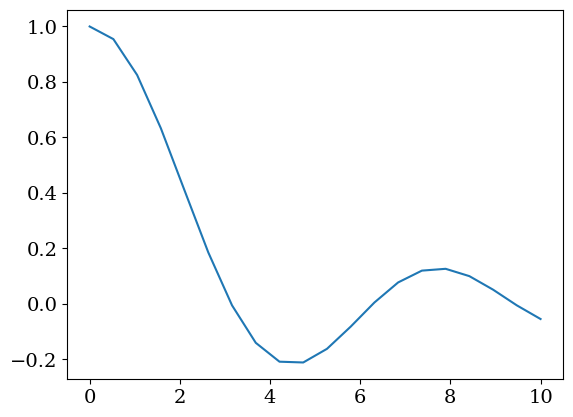
X = np.linspace(1.e-8,10.0,20)
Y = np.sin(X)/X
plt.plot(X,Y)
[<matplotlib.lines.Line2D at 0x7eff34267820>]
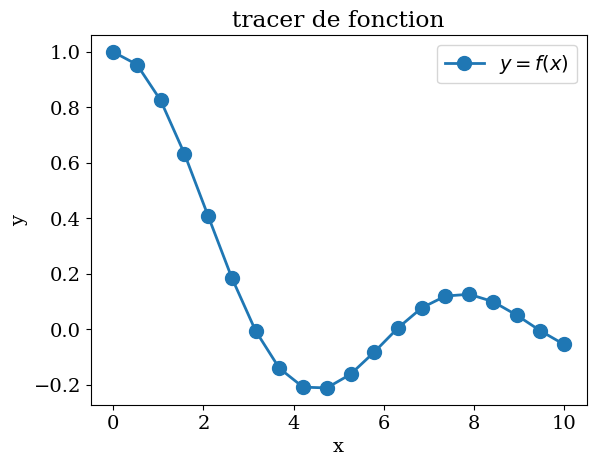
plt.plot(X,Y,'-',lw=2,marker="o",markersize=10,label="$y=f(x)$")
plt.title('tracer de fonction')
plt.xlabel('x')
plt.ylabel('y')
plt.legend()
<matplotlib.legend.Legend at 0x7eff321f76d0>
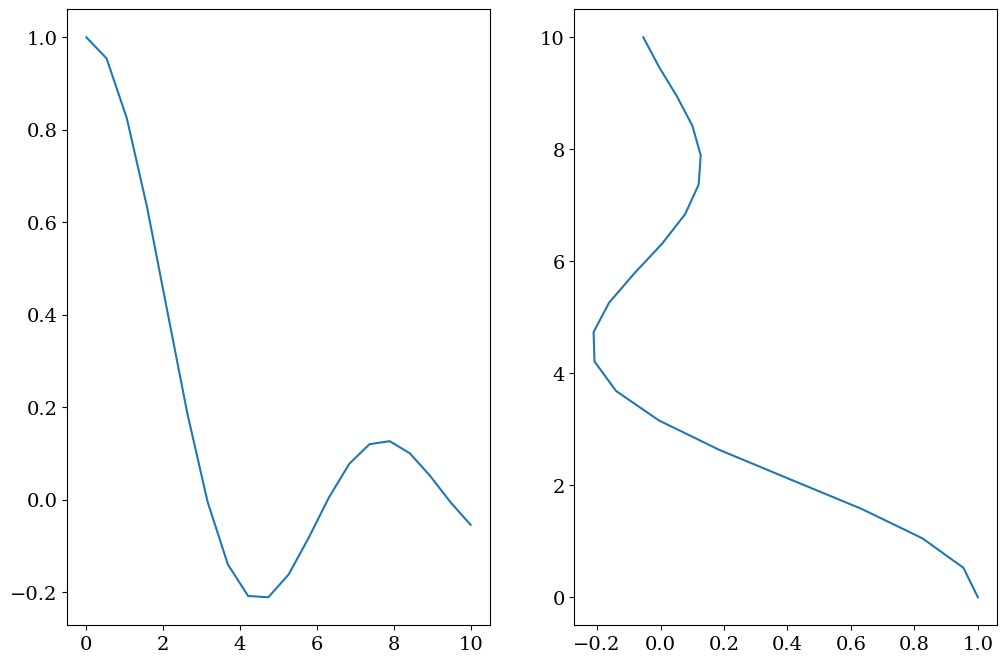
plt.figure(figsize=(12,8))
plt.subplot(1,2,1)
plt.plot(X,Y)
plt.subplot(1,2,2)
plt.plot(Y,X)
[<matplotlib.lines.Line2D at 0x7eff30f867d0>]
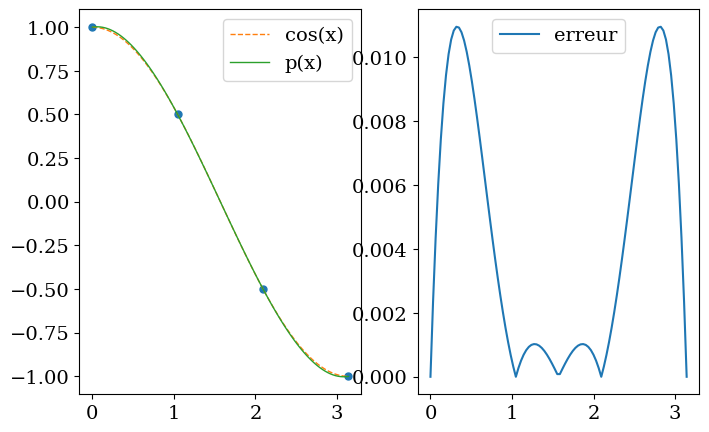
4.11.1. Exemple:#
Soit la fonction \(f(x)=cos(x)\) sur \([0,\pi]\). Calculer le polynome d’interpolation \(p(x)\) de degré N=4 de \(f(x)\) en utilisant des points équi-répartis. Tracer les points d’interpolation, le polynôme \(p(x)\) et la fonction \(f(x)\) sur un meme graphe, et l’erreur d’interpolation \(err=|f(x)-p(x)|\) sur un graphe à coté.
# solution
# calcul interpolation
Ni=4
Xi=np.linspace(0,np.pi,Ni)
Yi=np.cos(Xi)
M =np.ones((Ni,Ni))
for j in range(1,Ni):
M[:,j]=M[:,j-1]*Xi
Ai=solve(M,Yi)
# calcul
X=np.linspace(0,np.pi,100)
Y=np.cos(X)
YY=polynome(X,Ai)
# tracer
plt.figure(figsize=(8,5))
plt.subplot(1,2,1)
plt.plot(Xi,Yi,'o',markersize=5)
plt.plot(X,Y,'--',lw=1,label="cos(x)")
plt.plot(X,YY,'-',lw=1,label="p(x)")
plt.legend()
plt.subplot(1,2,2)
plt.plot(X,np.abs(Y-YY),label="erreur")
plt.legend()
<matplotlib.legend.Legend at 0x7eff30fc6290>
# implementation
4.12. tracer isovaleur 2D#
N=21
X=np.linspace(-np.pi,np.pi,N)
Y=np.linspace(-np.pi,np.pi,N)
Z=np.outer(np.sin(X),np.cos(Y))
plt.contourf(X,Y,Z)
<matplotlib.contour.QuadContourSet at 0x7eff30fe4f70>
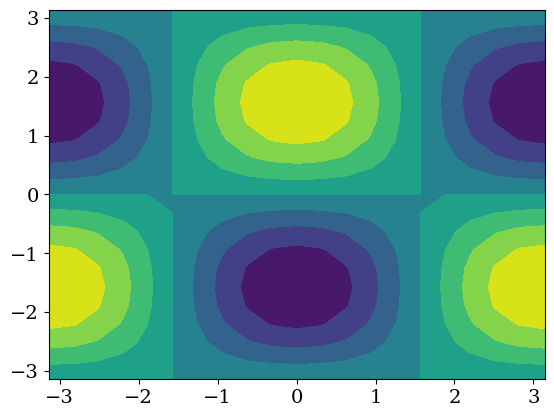
plt.contourf(X,Y,Z,11)
plt.axis('equal')
plt.colorbar()
plt.contour(X,Y,Z,11,colors='k')
<matplotlib.contour.QuadContourSet at 0x7eff30eb6b30>
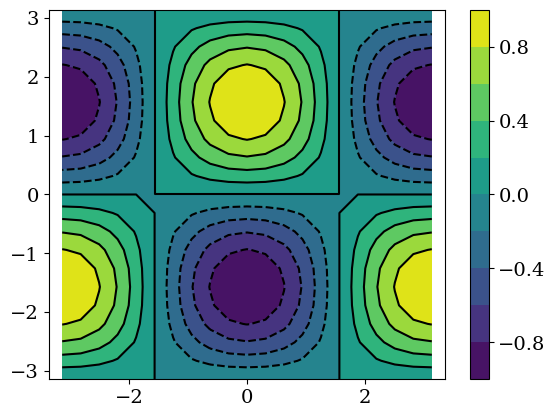
4.12.1. Exemple:#
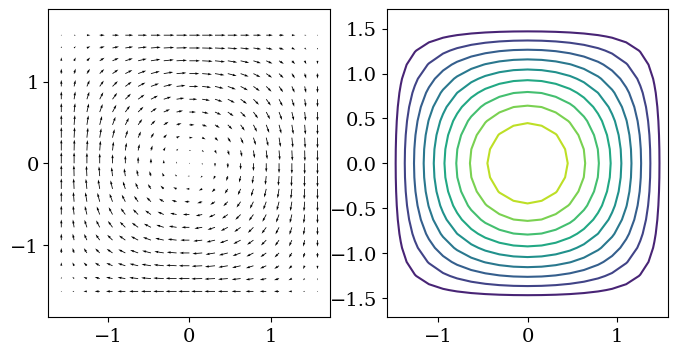
Soit le champ de vitesse correspondant à un tourbillon de Taylor dans \(\Omega=[-\pi/2,\pi/2]\times[-\pi/2,\pi/2]\) $\( U = cos(x)*sin(y) \mbox{ et } V=-sin(x)*cos(y) \)$
tracer le champ de vitesse en utilisant la fonction quiver de matplotlib
tracer la fonction de courant \(\psi = cos(x) cos(y) \) vérifiant $\( \frac{\partial \psi}{\partial y} = U \mbox { et } \frac{\partial \psi}{\partial x} = -V \)$
# solution
N=21
X,Y = np.meshgrid(np.linspace(-np.pi/2,np.pi/2,N),np.linspace(-np.pi/2,np.pi/2,N))
U = np.cos(X)*np.sin(Y)
V = -np.sin(X)*np.cos(Y)
Psi = np.cos(X)*np.cos(Y)
plt.figure(figsize=(8,4))
plt.subplot(1,2,1)
plt.quiver(X,Y,U,V)
plt.axis('equal')
plt.subplot(1,2,2)
plt.contour(X,Y,Psi,11)
plt.axis('equal')
(-1.5707963267948966,
1.5707963267948966,
-1.5707963267948966,
1.5707963267948966)
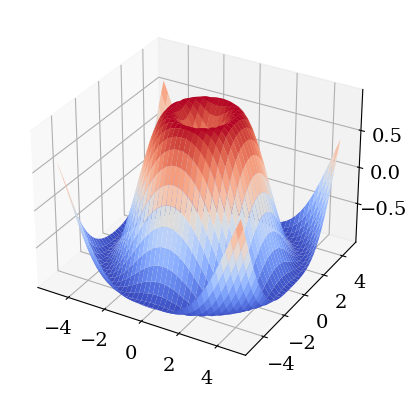
# solution
## 3D plot
from mpl_toolkits.mplot3d import Axes3D
from mpl_toolkits.mplot3d import Axes3D
from matplotlib import cm
fig = plt.figure()
ax = fig.add_subplot(projection='3d')
X = np.arange(-5, 5, 0.25)
Y = np.arange(-5, 5, 0.25)
X, Y = np.meshgrid(X, Y)
R = np.sqrt(X**2 + Y**2)
Z = np.sin(R)
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap=cm.coolwarm,
linewidth=0)
