7. Algorithmes d’IA#
Marc Buffat dpt mécanique, université Lyon 1
%matplotlib inline
import sys
import numpy as np
import matplotlib.pyplot as plt
# police des titres
plt.rc('font', family='serif', size='18')
from IPython.display import display,Markdown
import sklearn as sk
#sys.path.insert(1,"/home/cours/DatabaseIA")
from datasetIA import *
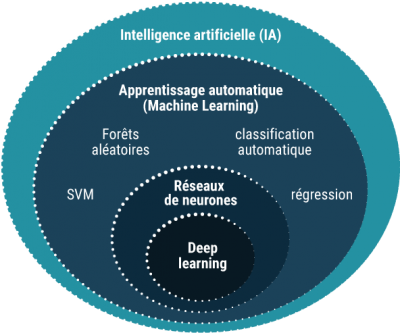
7.1. Problèmatique du machine learning#
problème : prédire une loi \(\mathcal{F}\)
à partir de l’apprentissage à l’aide d’une base de données de test \(\textbf{X}_i, Y_i\)
\(\rightarrow\) Problème de minimisation
Trouver la meilleur approximation \(\mathbf{F}\) minimisant l’erreur \(J\) sur la base de données de test.
\(J\) est une fonction coût du type:
\(\mathbf{F}(\mathbf{X}_i)\) est fonction d’une combinaison linéaire des données $\(\mathbf{F}(\mathbf{X}_i) = \mathbf{F}\left(\sum_j \beta_j \mathbf{X}_{i,j}\right)\)$
pas de forme explicite pour \(\mathbf{F}\) qui dépend de très nombreux paramètres à déterminer par une méthode de minimisation (de type gradient)
Algorithme implicite nécessitant des données annotées (i.e. avec le résultat) pour l’apprentissage et les tests de validation (apprentissage supervisée)
7.1.1. Méthodes de minimisation#
minimisation 1D (problème simple): 1 seul paramètre \(\beta\) tq \(F(\beta)\) soit minimum
solution exacte si \(F(\alpha)\) est quadratique:
sinon méthode de Brent (interpolation quadratique + bi-section)
lien calcul de racine d’une fonction et minimisation
minimisation ND (problème beaucoup plus complexes en particulier pour N grand): N paramètres \(\mathbf{X}=\left[\beta_j\right]\)
on peut se ramèner à des problèmes de minimisation 1D en choissisant des directions de descentes \(\mathbf{p_k}\)
minimiser \(F(\mathbf{X})\) avec \(X\in \mathcal{R}^N\)
répéter
choix direction \(\mathbf{p}_k\) (p.e. \(-\nabla \mathbf{X}\))
minimisation suivant \(\mathbf{p}_k\)
\[ \mbox{Trouvez $\alpha$ minimisant } F(\mathbf{X}_k + \alpha \mathbf{p}_k) \]nouvelle valeur de la solution \(\mathbf{X}_{k+1}\)
\[ \mathbf{X}_{k+1} = \mathbf{X}_k + \alpha_{opt} \mathbf{p}_k \]
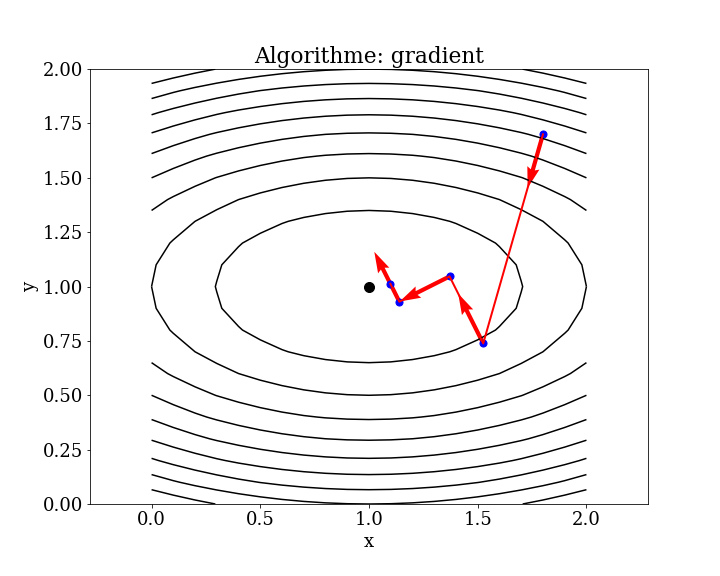
7.1.1.1. méthode de gradient local#
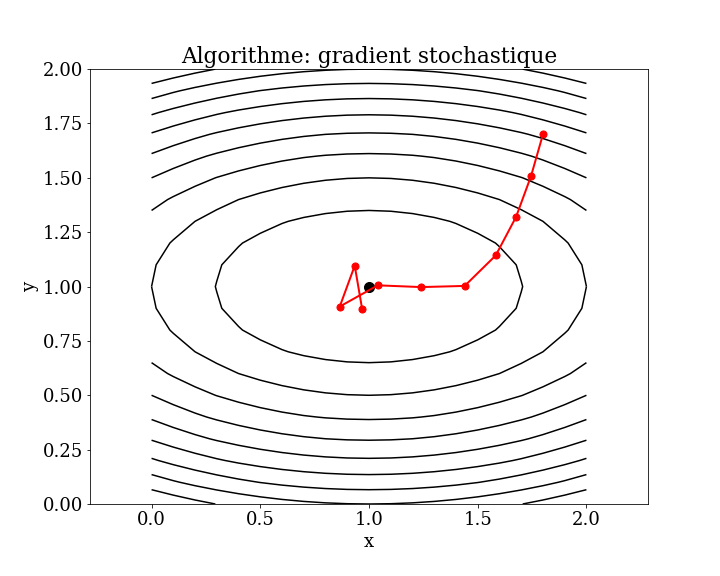
7.1.1.2. méthode de gradient stochastique (full batch)#
Cet algorithme est surtout utilisé pour minimiser une fonction coût avec un nombre très important de paramètres avec un taux d’apprentissage fixe.
7.1.2. Domaines d’applications du machine learning#
Traitement de données (expérimentales ou numériques)
Modélisation
Big Data
ATTENTION
ce n’est pas la solution pour tous les problèmes
méthodes classiques / semi-analytiques
à utiliser à bonne escient
7.2. Algorithmes de base#
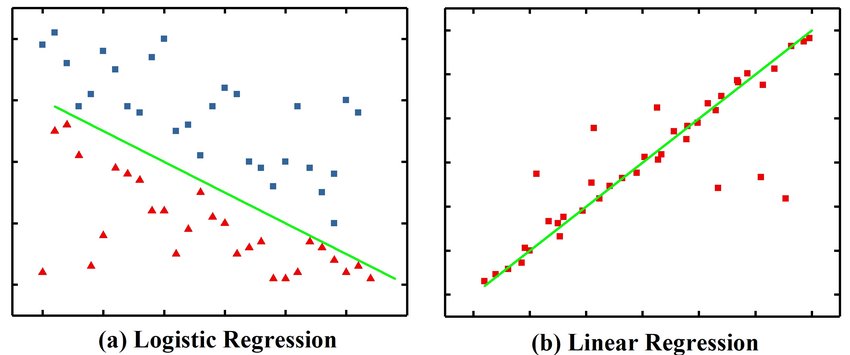
7.2.1. Linear Regression#
Régression linéaire par moindres carrés
LinearRegression ajuste un modèle linéaire avec des coefficients \(\mathbf{w} = (w_1, …, w_p)\) pour minimiser la somme des carrés résiduelle entre les cibles observées dans l’ensemble de données et les cibles prédites par l’approximation linéaire (méthodes des moindres carrés)
scikit learn model: LinearRegression
from sklearn.linear_model import LinearRegression
N = 11
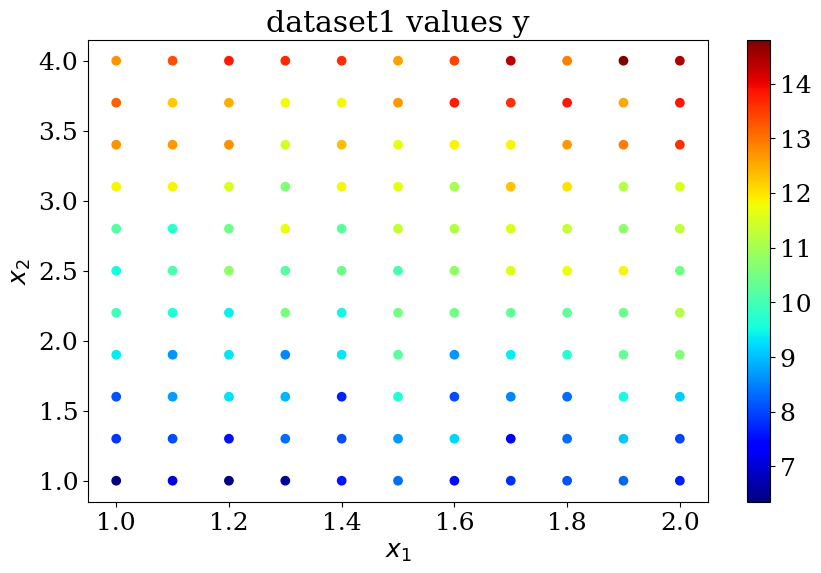
X,y = dataset1(N)
reg = LinearRegression().fit(X, y)
print("score = {:2d}%".format(int(100*reg.score(X, y))))
print("loi lineaire y = {:.2f} + {} X".format(reg.intercept_,reg.coef_))
score = 91%
loi lineaire y = 4.08 + [0.9950683 1.98990227] X
plot_data1(X,y,"dataset1 values y")
# prediction en x2=1
Xpred = np.array([[1,x] for x in np.linspace(1,4,21) ])
ypred = reg.predict(Xpred)
plot1(N,X,y,Xpred,ypred,titre="régression lineaire")
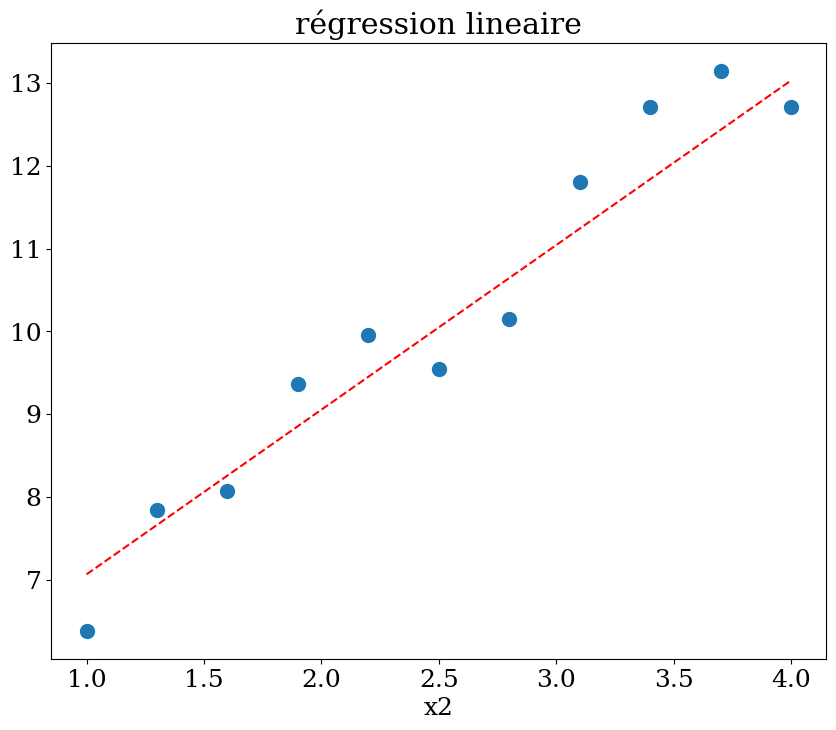
7.2.2. Logistic Regression#
La régression logistique, malgré son nom, est un modèle linéaire de classification plutôt que de régression. La régression logistique est également connue dans la littérature sous le nom de régression logit, de classification à entropie maximale (MaxEnt) ou de classifieur log-linéaire. Dans ce modèle, les probabilités décrivant les résultats possibles d’un seul essai sont modélisées à l’aide d’une fonction logistique
scikit learn model LogisticRegression
La régression logistique est un algorithme de classification simple et efficace, qui ne nécessite pas une grande puissance de calcul et est facile à mettre en œuvre. Ce modèle d’apprentissage est largement utilisé par les analystes de données et les scientifiques.
La régression logistique, malgré son nom, est un modèle linéaire de classification plutôt que de régression. La régression logistique est également connue dans la littérature sous le nom de « logit régression », de « classification à entropie maximale » (MaxEnt) ou de « classificateur log-linéaire ». Dans ce modèle, les probabilités décrivant les résultats possibles d’un seul essai sont modélisées à l’aide d’une fonction logistique.
La régression logistique est implémentée dans LogisticRegression. Cette implémentation peut s’adapter à une régression logistique binaire, One-vs-Rest ou multinomiale avec régularisation facultative (l1, l2, elasticnet, aucune)
7.2.3. Régression logistique#
La régression logistique est une méthode statistique de prédiction des classes binaires. Le résultat ou la variable cible est de nature dichotomique. Dichotomique signifie qu’il n’y a que deux classes possibles. Il calcule la probabilité d’occurrence d’un événement.
Il s’agit d’un cas particulier de régression linéaire où la variable cible est de nature catégorielle. Il utilise un journal des cotes comme variable dépendante. La régression logistique prédit la probabilité d’occurrence d’un événement binaire à l’aide d’une fonction logit.
Equation linéaire de régression
Fonction sigmoide
probalité y=1
Limites
La régression logistique n’est pas adaptée à un grand nombre de caractéristiques. Cet algorithme ne peut pas résoudre le problème de non-linéarité ce qui nécessite la transformation des caractéristiques non linéaires. Ainsi, la régression logistique ne fonctionne pas bien avec des variables indépendantes qui ne sont pas corrélées à la variable cible et qui sont très similaires entre elles.
from sklearn.linear_model import LogisticRegression
N = 10
X,y,col = dataset2(N)
clf = LogisticRegression(random_state=0).fit(X, y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 98%
# prediction
NN = 21
Xpred, ypred, colpred = predict2(NN,clf.predict)
plot2(X,col, Xpred,colpred, titre="Logistic régréssion")
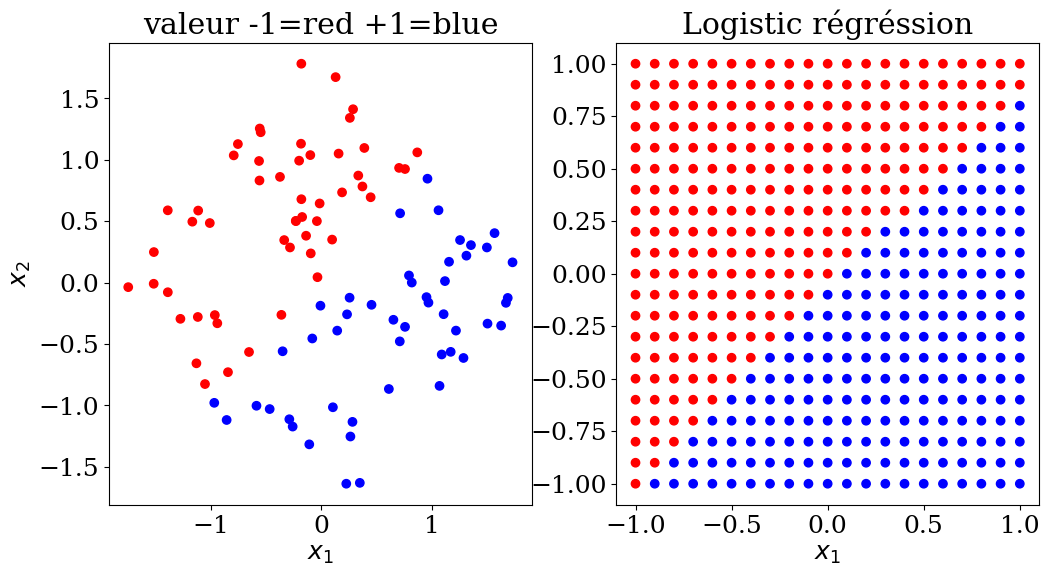
7.2.4. Arbres de décisions (Decision Trees)#
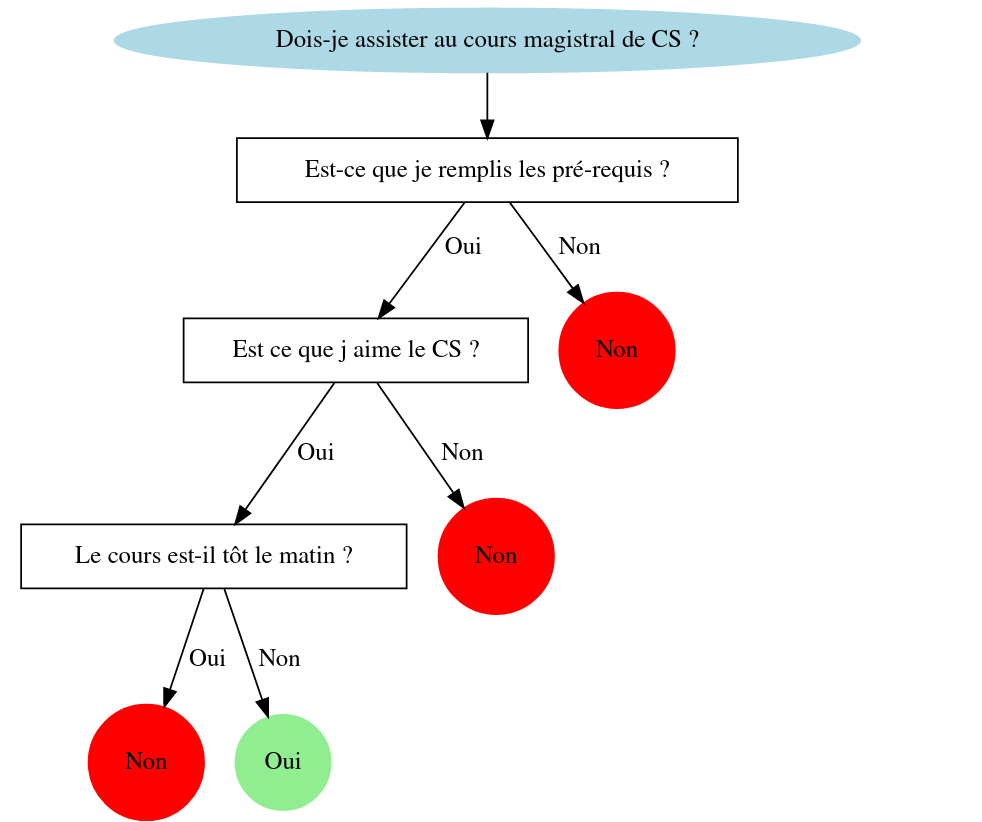
Pour faire une prédiction, les arbres de décisions utilisent un ensemble de règles de décision « If Then Else » sur les features (données). Cette méthode permet de décomposer un ensemble de données en sous-ensembles de plus en plus petits. On peut ainsi assigner aux sous-ensemble finaux une classe (0 ou 1 pour une classification binaire). Le but du modèle va être de créer des sous-ensembles homogènes (contenant des exemples de même classe) pour minimiser l’erreur de ses prédictions.
classification
scikit learn model DecisionTreeClassifier
regression
scikit learn model DecisionTreeRegressor
Problème : résultat dépend de l’ordre des questions!
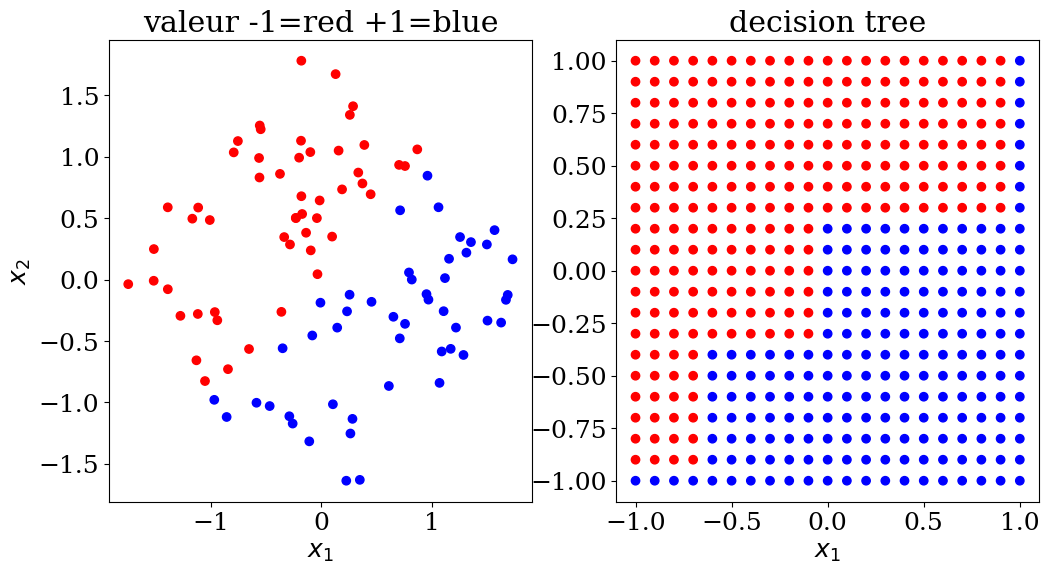
7.2.4.1. Decision tree: classification#
scikit learn DecisionTreeClassifier
from sklearn.tree import DecisionTreeClassifier
N = 10
X,y,col = dataset2(N)
clf = DecisionTreeClassifier()
clf = clf.fit(X, y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 100%
# prediction
NN = 21
Xpred, ypred, colpred = predict2(NN, clf.predict)
plot2(X,col, Xpred,colpred,titre="decision tree")
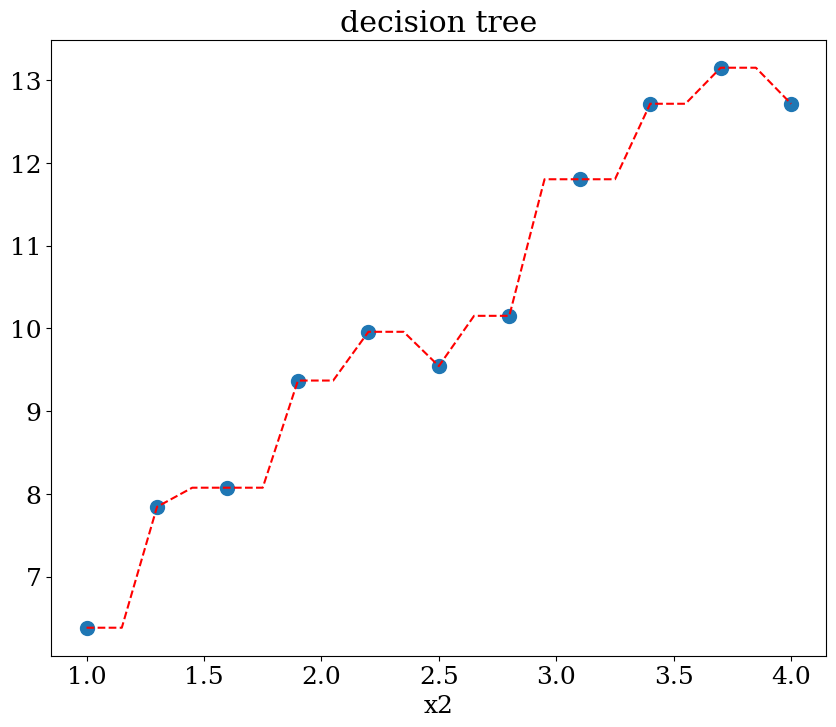
7.2.4.2. Décision tree: régression#
scikit learn DecisionTreeRegressor
from sklearn.tree import DecisionTreeRegressor
N = 11
X,y = dataset1(N)
clf = DecisionTreeRegressor()
clf = clf.fit(X, y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 100%
# prediction en x2=1
NN = 51
Xpred = np.array([[1,x] for x in np.linspace(1,4,21) ])
ypred = clf.predict(Xpred)
plot1(N,X,y, Xpred,ypred,titre="decision tree")
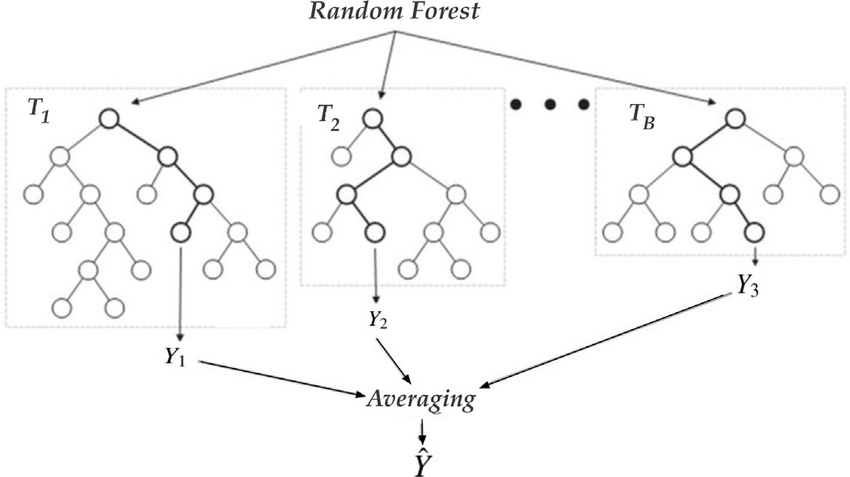
7.2.5. Forêts d’arbres décisionnels: (Random forest)#
Les modèles Random Forest sont composés de plusieurs Decision Trees (“forêt” d’arbres de décision). Le résultat retourné par un Random Forest est la classe majoritaire retournée par les Decision Trees qui le composent. Ces Decision Trees sont chacuns entraînés avec un échantillon des données d’entraînement pris au hasard et un sous-ensemble des features pris au hasard également.
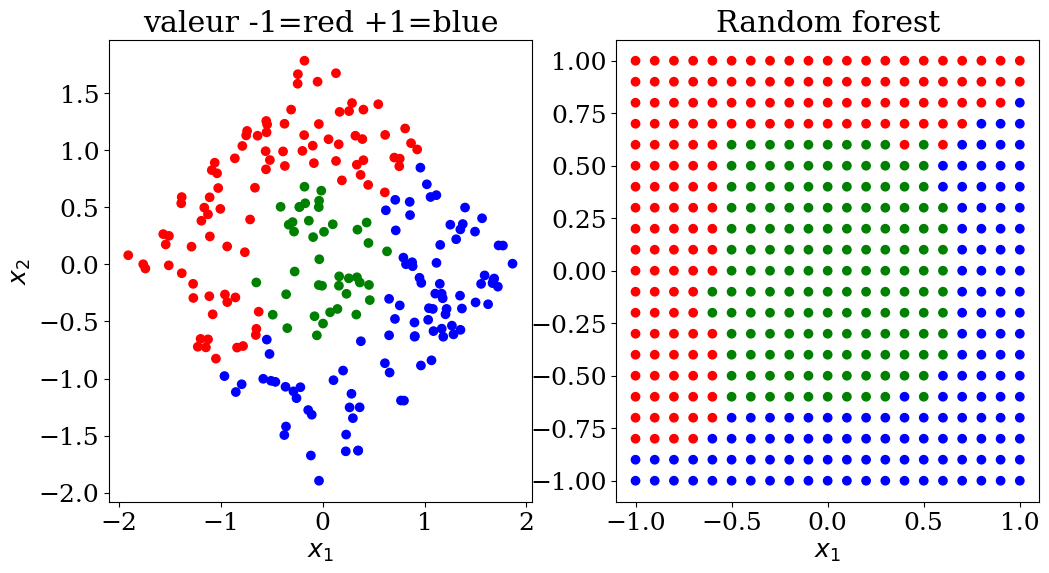
7.2.5.1. Random forest classification#
scikit learn RandomForestClassifier
utilisation dataset3 avec 3 ensembles de valeurs (-1,0,+1)
influence des paramètres:
max_deph: profondeur de l’arbre 2, 3 ou None
from sklearn.ensemble import RandomForestClassifier
N=15
X,y,col = dataset3(N)
clf = RandomForestClassifier(max_depth=None, random_state=0)
cfl = clf.fit(X, y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 100%
# prediction
NN = 21
Xpred,ypred,colpred = predict3(NN, clf.predict)
plot3(X,col, Xpred,colpred, titre="Random forest")
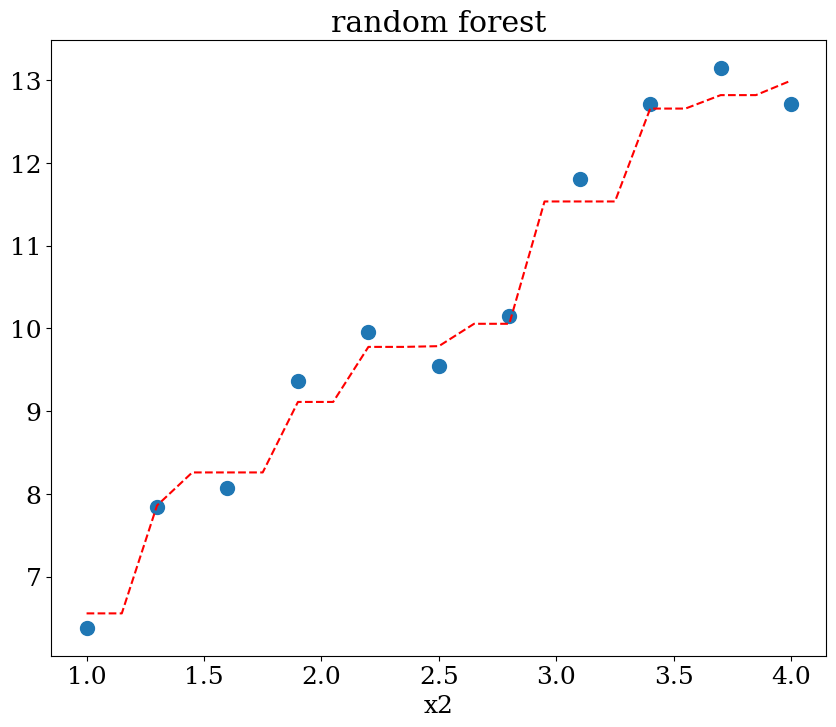
7.2.5.2. Random forest régression#
scikit learn RandomForestRegression
influence des paramètres:
max_deph: profondeur de l’arbre 2, 3 ou None
from sklearn.ensemble import RandomForestRegressor
N=11
X,y = dataset1(N)
clf = RandomForestRegressor(max_depth=None, random_state=0)
cfl = clf.fit(X, y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 98%
NN = 51
Xpred = np.array([[1,x] for x in np.linspace(1,4,21) ])
ypred = clf.predict(Xpred)
plot1(N,X,y, Xpred,ypred,titre="random forest")
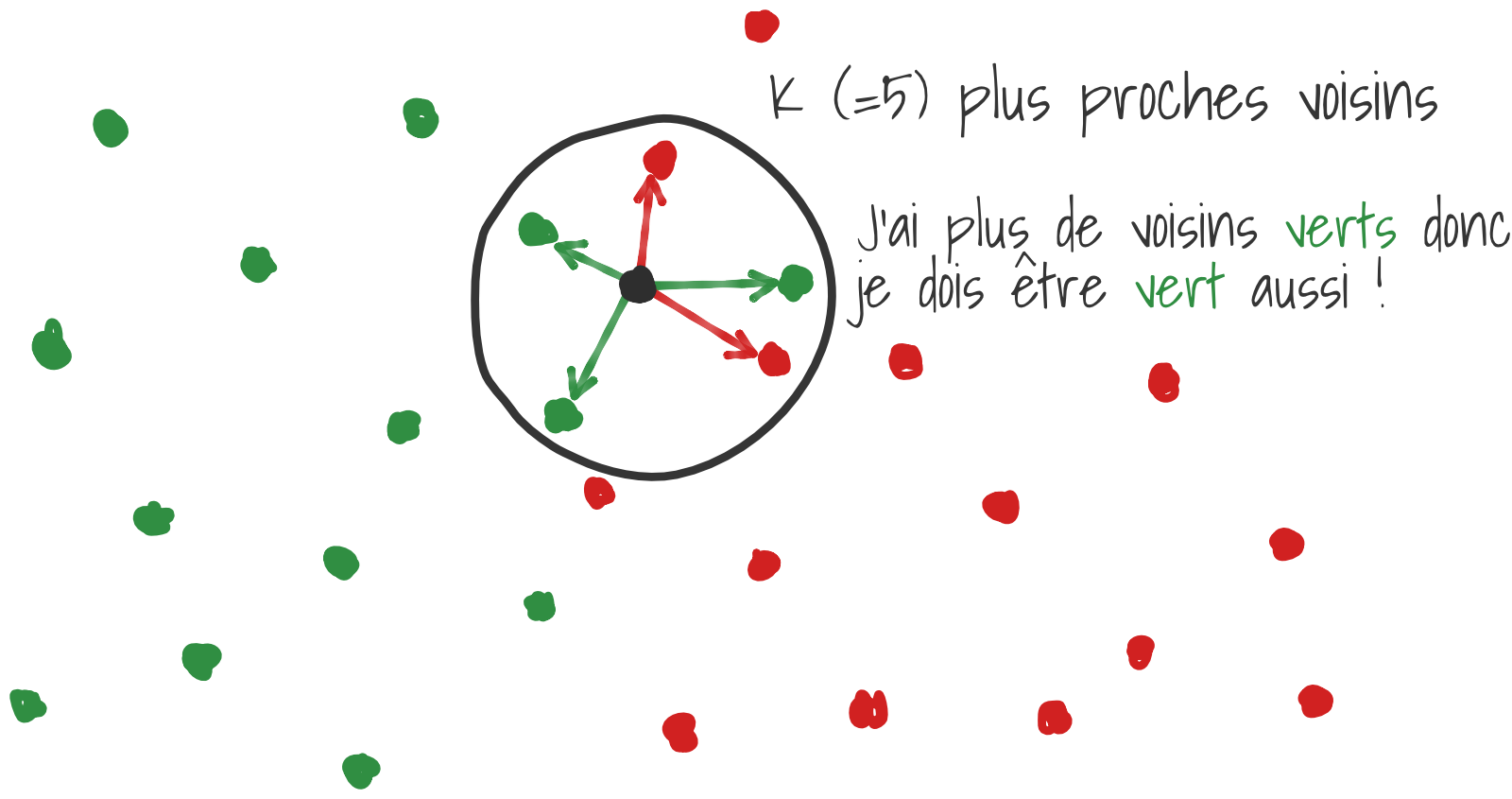
7.2.6. K plus proches voisins (KNN)#
L’algorithme des KNN (“K plus proches voisins” en français) attribue à un exemple la classe majoritaire parmi ses K plus proches voisins. K est un paramètre à optimiser par l’utilisateur, il est préférable de choisir un K impair pour de la classification binaire pour éviter les égalités. On utilise communément la distance euclidienne entre deux vecteurs de features pour calculer la proximité entre 2 exemples.
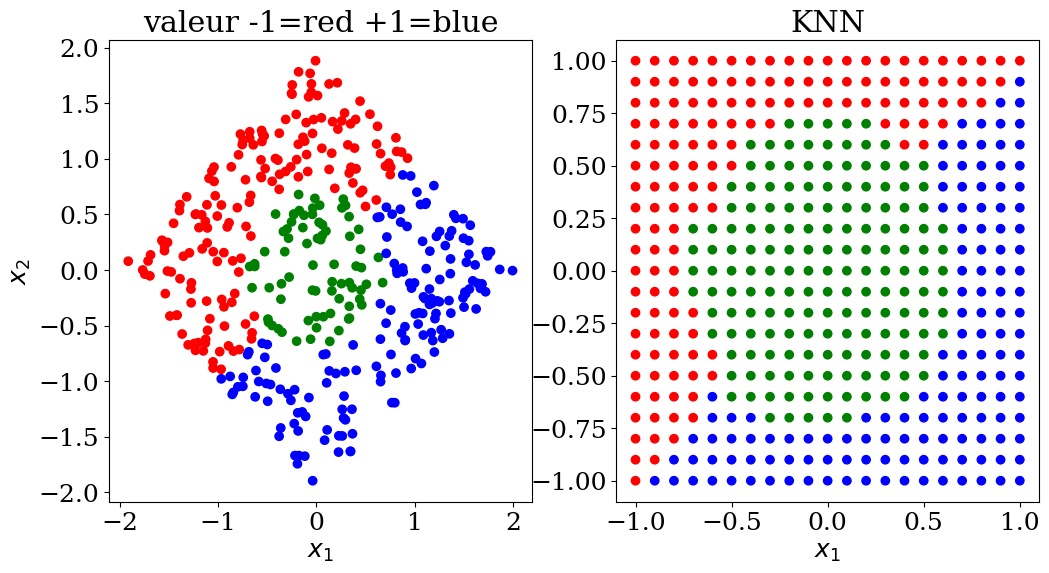
7.2.6.1. KNN classification#
scikit learn KNeighborsClassifier
paramètres:
n_neighbors = 2,3,..5
from sklearn.neighbors import KNeighborsClassifier
N = 20
X,y,col = dataset3(N)
neigh = KNeighborsClassifier(n_neighbors=5)
neigh = neigh.fit(X, y)
print("score = {:2d}%".format(int(100*neigh.score(X, y))))
score = 98%
# prediction
NN = 21
Xpred,ypred,colpred = predict3(NN, neigh.predict)
plot3(X,col, Xpred,colpred, titre="KNN")
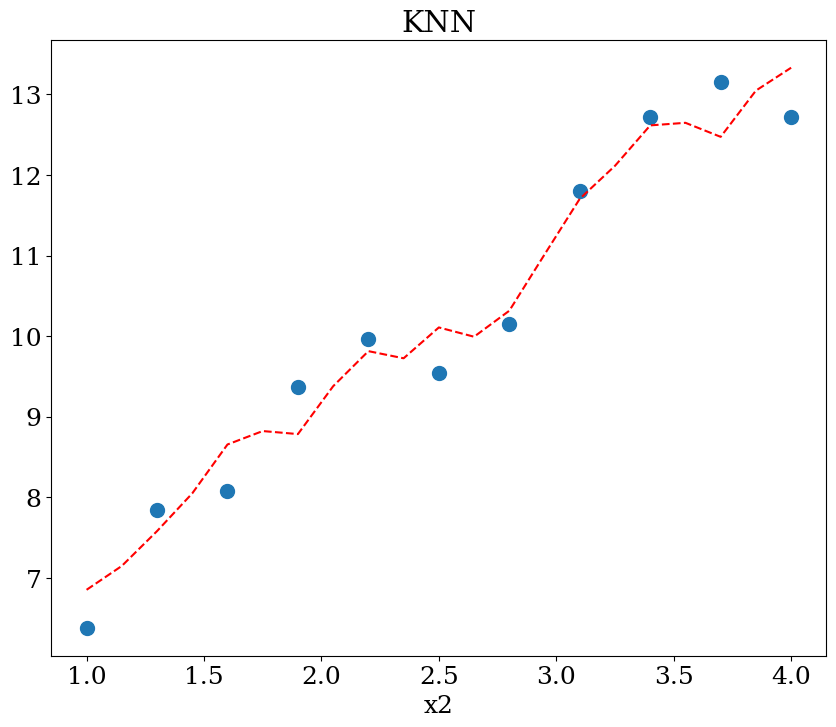
7.2.6.2. KNN régression#
scikit learn KNeighborsRegressor
paramètres:
n_neighbors = 2,3,..5
from sklearn.neighbors import KNeighborsRegressor
N=11
X,y = dataset1(N)
neigh = KNeighborsRegressor(n_neighbors=5)
neigh = neigh.fit(X, y)
print("score = {:2d}%".format(int(100*neigh.score(X, y))))
score = 93%
NN = 51
Xpred = np.array([[1,x] for x in np.linspace(1,4,21) ])
ypred = neigh.predict(Xpred)
plot1(N,X,y, Xpred,ypred,titre="KNN")
7.2.7. Support vector machine SVM#
Les machines à vecteurs de support (SVM) sont un ensemble de méthodes d’apprentissage supervisé utilisées pour la classification, la régression et la détection des valeurs aberrantes. Ce sont des classes capables d’effectuer une classification binaire et multiclasse sur un ensemble de données.
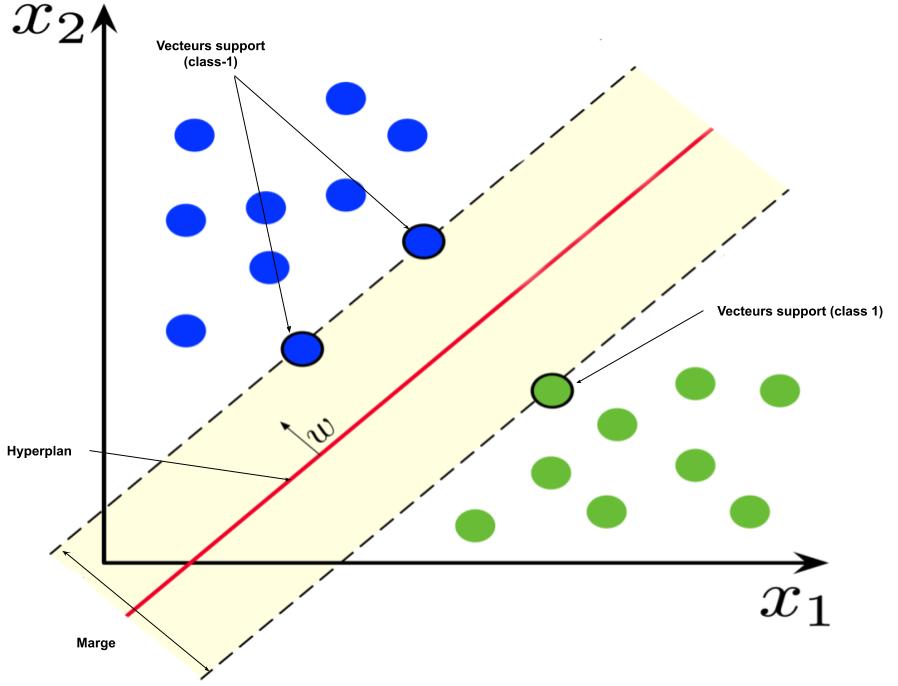
Les séparateurs à vastes marges (SVM) sont des classificateurs qui reposent sur deux idées clés (Wikipedia).
La première idée clé est la notion de marge maximale. La marge est la distance entre la frontière de séparation et les échantillons les plus proches. Ces derniers sont appelés vecteurs supports. Dans les SVM, la frontière de séparation est choisie comme celle qui maximise la marge. Le problème est de trouver cette frontière séparatrice optimale, à partir d’un ensemble d’apprentissage. Ceci est fait en formulant le problème comme un problème d’optimisation quadratique, pour lequel il existe des algorithmes connus.
7.2.7.1. Support vector machines SVM#
scikit learn svm
from sklearn import svm
N = 20
X,y,col = dataset3(N)
clf = svm.SVC()
clf = clf.fit(X,y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 99%
# prediction
NN = 21
Xpred, ypred, colpred = predict3(NN, clf.predict)
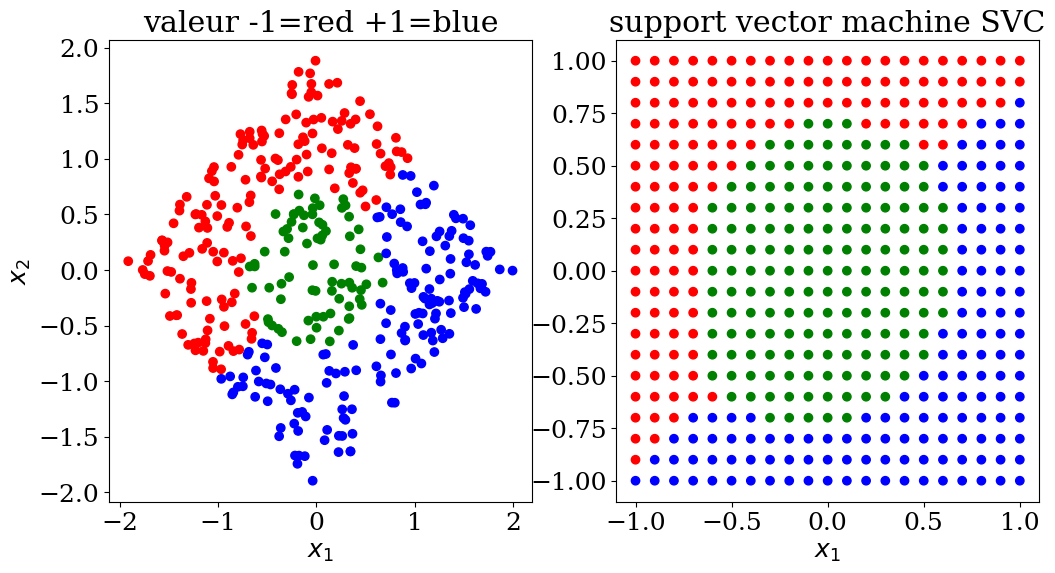
plot3(X,col, Xpred,colpred, titre="support vector machine SVC")
7.3. Réseaux de neurones en IA#

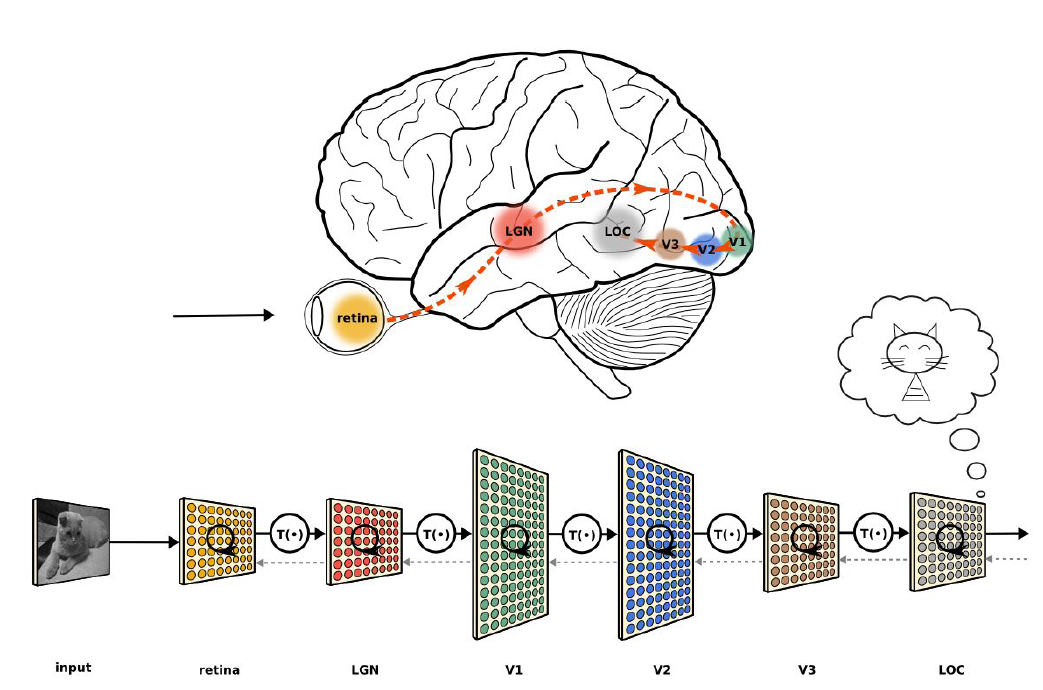
7.3.1. Apprentissage Deep Learning#
analogie (un peu fausse) avec le cerveau !
7.4. Neurone (informatique)#
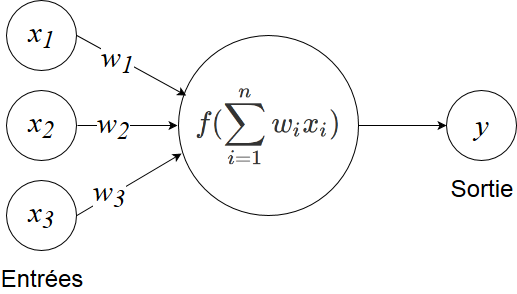
f est la fonction d’activation
Elle permet de passer d’un modèle linéaire à un modèle non-linéaire (donc de modéliser des relations plus complexes)
Elle permet aussi de contrôle des sorties: bornage (entre 0 et 1 pour la sigmoïde, entre -1 et 1 pour la tanh)
La fonction ReLU permet un apprentissage plus efficace dans les couches cachées (évite le problème du gradient qui disparaît).
7.4.1. Fonctions d’activation couramment utilisées#
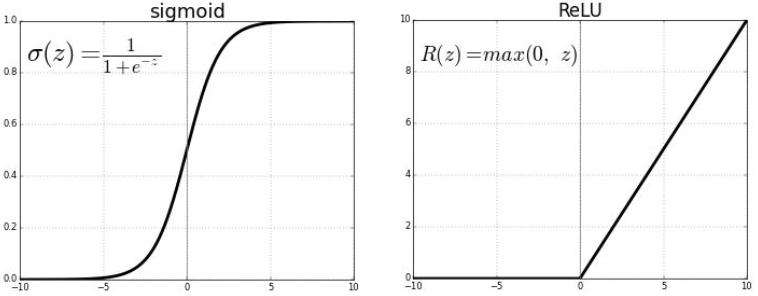
à gauche utilisation : à mettre en fin de réseau pour prédire une probabilité (entre 0 et 1)
à droite utilisation : entre chaque couche pour dé-linéariser (à coût de calcul faible)
7.4.2. Neurone formel#
le neurone formel est un modèle qui se caractérise par des signaux d’entrée \(\mathbf{x}=[x_1,...,x_p]\) et une fonction d’activation \(f\) pour calculer la sortie \(y\) :
La fonction d’activation opère une transformation d’une combinaison affine des signaux d’entrée, \(\alpha_0\), terme constant, étant appelé le biais du neurone. Cette combinaison affine est déterminée par un vecteur de poids \(\mathbf{\alpha}=[\alpha_1,..\alpha_2]\) associé à chaque neurone et dont les valeurs sont estimées dans la phase d’apprentissage. Ils constituent la mémoire ou connaissance répartie du réseau.
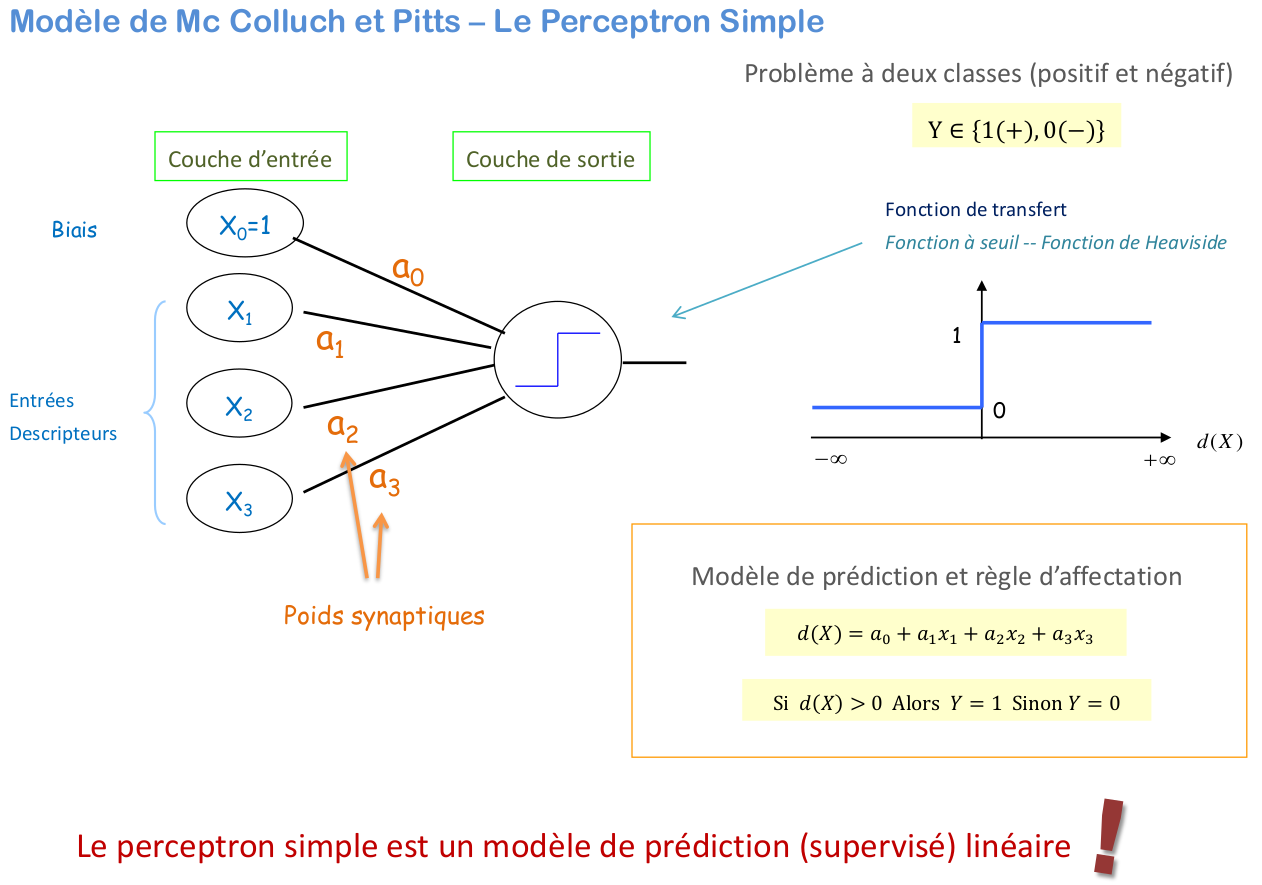
7.5. Couches de neurones / layers#

à gauche : profondeur = 1
à droite : profondeur = 2
7.5.1. formalisme: perceptron multicouche#
Le perceptron multicouche (PMC) est un réseau composé de couches successives. Une couche est un ensemble de neurones n’ayant pas de connexion entre eux. Une couche d’entrée lit les signaux entrant, un neurone par entrée \(x_j\) , une couche en sortie fournit la réponse du système \(Y\).
Les p entrées ou variables explicatives du modèle sont notées \(X_1,...,X_p\) tandis que la sortie est la variable Y à expliquer ou cible du modèle.
De façon usuelle et en régression (Y quantitative), la dernière couche est constituée d’un seul neurone muni de la fonction d’activation identité tandis que les autres neurones (couche cachée) sont munis de la fonction sigmoïde.
Ce modèle inclut des couches non linéaires « cachées ». Le nom « caché » ici signifie simplement pas directement connecté aux entrées ou sorties.
7.5.1.1. perceptron à une couche cachée#
Ainsi, en régression avec un perceptron à une couche cachée de q neurones et un neurone de sortie, cette fonction s’écrit:
Les poids des entrées sont les paramètres \(\mathbf{\alpha},\mathbf{\beta}\) à estimer lors de la procédure d’apprentissage. Un perceptron multicouche réalise donc une transformation des variables d’entrée \(\mathbf{X}\):
où \(\mathbf{\alpha}\) est le vecteur contenant chacun des paramètres \(\alpha_{jkl}\) de la jème entrée du kème neurone de la lème couche et \(\beta\) les paramètres de la couche de sortie.
résultat théorique
Un théorème dit d’approximation universelle montre que cette structure élémentaire à une seule couche cachée est suffisante pour prendre en compte les problèmes classiques de modélisation ou apprentissage statistique. En effet, toute fonction régulière peut être approchée uniformément avec une précision arbitraire et dans un domaine fini de l’espace de ses variables, par un réseau de neurones comportant une couche de neurones cachés en nombre fini possédant tous la même fonction d’activation et un neurone de sortie linéaire.
attention on ne dit pas comment !
7.6. Apprentissage avec un réseau de neurones#
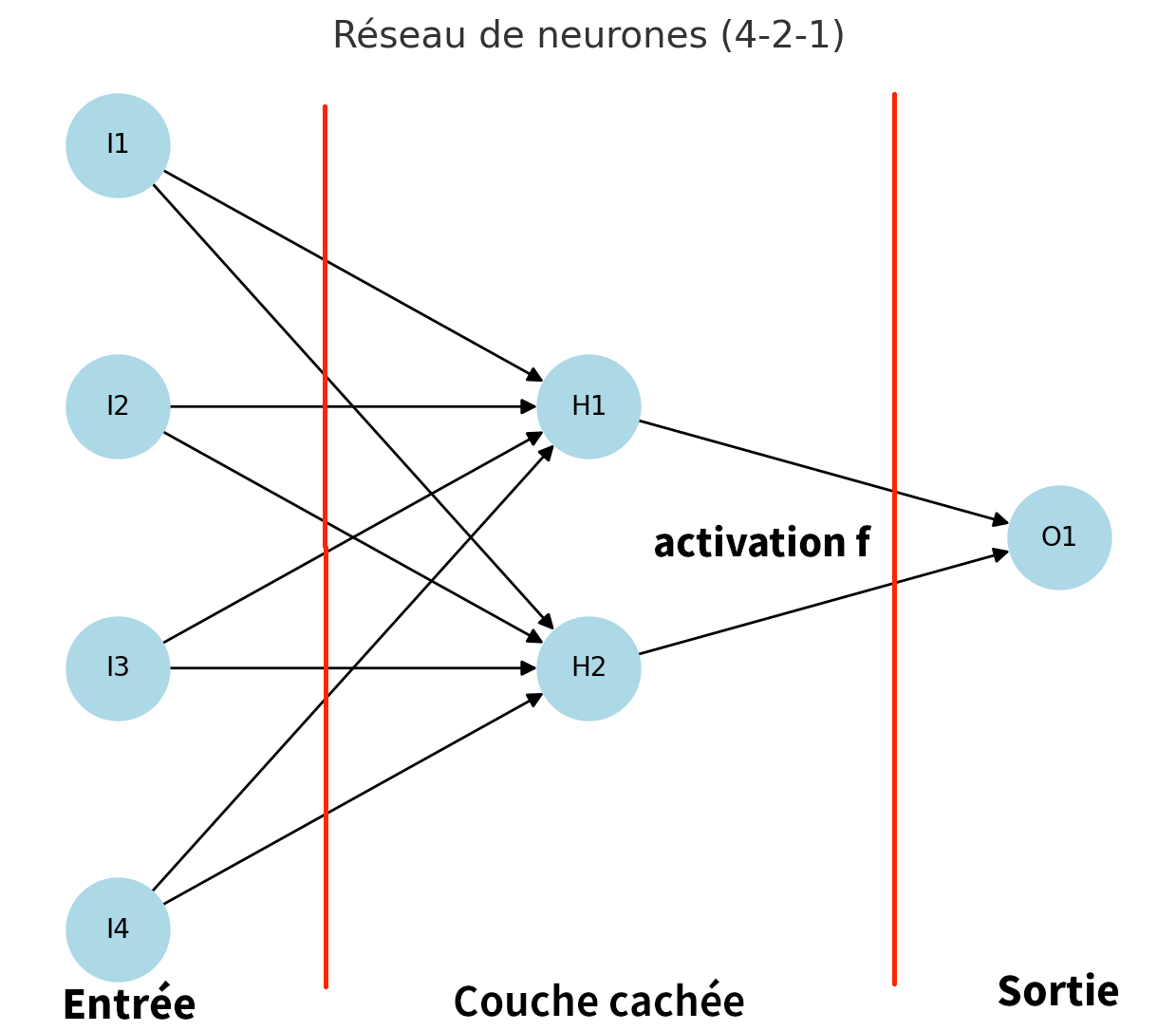
Considérons un réseau de neurones avec p=4 entrées (\(I1-I4\)), 1 couche cachée de q=2 neurones (\(H1-H2\)), et r=1 sortie (\(O1\)) avec une fonction d’activation f pour la couche cachée et une sortie linéaire pour une régression.
On a donc les relations suivantes:
Ce modèle dépend donc des 13 paramètres suivants:
vecteur (2) \(\mathbf{B^1}={b^1}_{k=1,2}\)
matrice (4,2) \(\mathbf{W^1}={w^1}_{k,i}\)
vecteur (1) \(\mathbf{W^1}={b^2}\)
matrice (2,1} \(\mathbf{W^2}={w^2_j}\)
On dispose d’une base d’apprentissage de taille n d’observations \((x^1_i ,...,x^4_i ; y_i)\). On note \(X_1,X_2,X_3,X_4\) les vecteurs donnés et \(Y\) la variable à prévoir (résultat Ypred)
Dans notre cas simple de la régression avec un réseau constitué d’un neurone de sortie linéaire et d’une couche cachée à q=2 neurones, pour une couche d’entrée de dimension p, les paramètres sont optimisés par moindres carrés. Ceci se généralise à toute fonction perte dérivable et donc à la discrimination à m classes.
L’apprentissage correspond à l’estimation des paramètres par minimisation de la fonction perte quadratique \(J\) (ou de celle d’une fonction d’entropie dans le cas d’une classification)
Les relations pour le calcul de la prédiction Ypred en fonction des donnes X1,X2,X3,X4 s’écrivent:
d’où la fonction coût \(J\) (erreur quadratique ou loss) s’écrit:
dont la variation par rapport aux paramètres d’écrit:
avec
On en déduit les composantes du gradient:
7.6.1. Forme matricielle#
Le réseau de neuronne 4-2-1 s’écrit:
ce qui donne le modèle \(Y=F(\mathbf{X})\) écrit matriciellement:
et la fonction cout (erreur quadratique moyenne)
7.6.2. Minimisation sous forme matricielle#
Différents algorithmes d’optimisation peuvent être utilisés, ils sont généralement basés sur une évaluation numérique du gradient (stochastique gradient) par un algorithme de rétro-propagation:
Algorithme de minimisation
Initialisation
Début des itérations (nbre d’Epoch)
Calcul de l’erreur J (loss) (forward)
calcul de la prédiction Ypred pour les valeurs de la BD X par un algorithme de parcours en avant (forward) du réseau
d’où la valeur prédite \( Ypred = \mathbf{A_2}\) et l’erreur loss=J
Évaluation du gradient (backward)
- Évaluation stochastique de la valeur du gradient par un algorithme de parcours en arrière (backwards) du réseau
Calcul de la nouvelle valeur des paramètres par descente avec un pas fixe \(\alpha\) (learning_rate)
fin itération (retour étape 1)
Remarques
les calculs s’écrivent sous forme vectorielle et peuvent donc être optimisées efficacement sur GPU
calcul efficace du gradient par « backpropagation »
on estime le « gradient » échantillon par échantillon, ou par mini-batches de quelques échantillons
une passe complète sur le jeu de données s’appelle « Epoch »
le nombre d’ »Epochs » est donc le nombre de passes effectuées sur le jeu d’entraînement lors de l’apprentissage
7.6.3. Implémentation simple d’un réseau avec 1 couche#
fonction activation ReLU
application à la prédiction de la fonction sin(x) sur \([0,\pi]\) avec un réseau 1-20-1
code généré avec l’aide de ChatGPT
import numpy as np
import matplotlib.pyplot as plt
# Activation functions
def relu(x):
return np.maximum(0, x)
def relu_deriv(x):
return (x > 0).astype(float)
# Mean Squared Error
def mse_loss(y_pred, y_true):
return np.mean((y_pred - y_true) ** 2)
def mse_deriv(y_pred, y_true):
return (y_pred - y_true) / y_true.shape[0]
# Réseau de neurones
class NeuralNetwork:
def __init__(self, input_size, hidden_size, output_size):
# Xavier initialization
self.W1 = np.random.randn(input_size, hidden_size) * np.sqrt(1. / input_size)
self.b1 = np.zeros((1, hidden_size))
self.W2 = np.random.randn(hidden_size, output_size) * np.sqrt(1. / hidden_size)
self.b2 = np.zeros((1, output_size))
def forward(self, X):
self.Z1 = X @ self.W1 + self.b1
self.A1 = relu(self.Z1)
self.Z2 = self.A1 @ self.W2 + self.b2 # sortie linéaire
self.A2 = self.Z2
return self.A2
def backward(self, X, y_true, learning_rate=0.01):
m = X.shape[0]
dZ2 = mse_deriv(self.A2, y_true)
dW2 = self.A1.T @ dZ2
db2 = np.sum(dZ2, axis=0, keepdims=True)
dA1 = dZ2 @ self.W2.T
dZ1 = dA1 * relu_deriv(self.Z1)
dW1 = X.T @ dZ1
db1 = np.sum(dZ1, axis=0, keepdims=True)
# Gradient descent update
self.W2 -= learning_rate * dW2
self.b2 -= learning_rate * db2
self.W1 -= learning_rate * dW1
self.b1 -= learning_rate * db1
def train(self, X, y, epochs=2000, learning_rate=0.01):
for epoch in range(epochs):
y_pred = self.forward(X)
loss = mse_loss(y_pred, y)
self.backward(X, y, learning_rate)
if epoch % 200 == 0:
print(f"Epoch {epoch}, Loss: {loss:.6f}")
def predict(self, X):
return self.forward(X)
# ====== Expérience : approximation de sin(x) ======
# Données
X = np.linspace(0, np.pi, 100).reshape(-1, 1)
y = np.sin(X)
# Modèle
model = NeuralNetwork(input_size=1, hidden_size=20, output_size=1)
model.train(X, y, epochs=3000, learning_rate=0.01)
# Prédictions
y_pred = model.predict(X)
# Visualisation
plt.figure(figsize=(8,5))
plt.plot(X, y, label="sin(x)", linewidth=2)
plt.plot(X, y_pred, label="Prédiction NN", linestyle="--")
plt.legend()
plt.title("Approximation de sin(x) par un réseau de neurones (1-20-1)")
plt.show()
Epoch 0, Loss: 0.203108
Epoch 200, Loss: 0.116715
Epoch 400, Loss: 0.088899
Epoch 600, Loss: 0.076416
Epoch 800, Loss: 0.069374
Epoch 1000, Loss: 0.064302
Epoch 1200, Loss: 0.059938
Epoch 1400, Loss: 0.055801
Epoch 1600, Loss: 0.051745
Epoch 1800, Loss: 0.047758
Epoch 2000, Loss: 0.043826
Epoch 2200, Loss: 0.040014
Epoch 2400, Loss: 0.036330
Epoch 2600, Loss: 0.032818
Epoch 2800, Loss: 0.029523
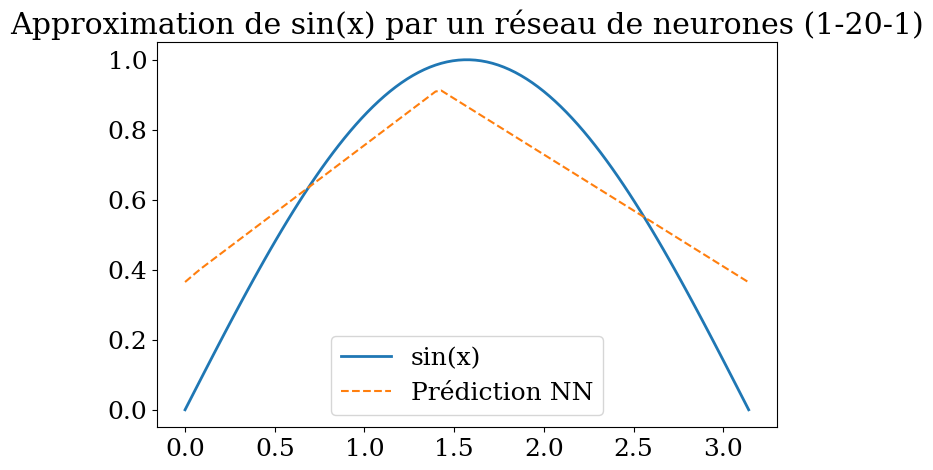
7.6.4. Amélioration#
réseau multicouche
fonction activation tanh
application prédiction sin(x) avec un réseau 1-20-20-1
import numpy as np
import matplotlib.pyplot as plt
# Activation functions
def tanh(x):
return np.tanh(x)
def tanh_deriv(x):
return 1 - np.tanh(x)**2
# Mean Squared Error
def mse_loss(y_pred, y_true):
return np.mean((y_pred - y_true) ** 2)
def mse_deriv(y_pred, y_true):
return (y_pred - y_true) / y_true.shape[0]
# Réseau de neurones multi-couches avec tanh
class NeuralNetwork:
def __init__(self, layer_sizes):
"""
layer_sizes = [input_size, hidden1, hidden2, ..., output_size]
"""
self.num_layers = len(layer_sizes) - 1
self.W = []
self.b = []
for i in range(self.num_layers):
in_size = layer_sizes[i]
out_size = layer_sizes[i+1]
# Xavier init
self.W.append(np.random.randn(in_size, out_size) * np.sqrt(1. / in_size))
self.b.append(np.zeros((1, out_size)))
def forward(self, X):
self.Z = []
self.A = [X]
for i in range(self.num_layers - 1): # couches cachées
z = self.A[-1] @ self.W[i] + self.b[i]
a = tanh(z)
self.Z.append(z)
self.A.append(a)
# Dernière couche (linéaire)
z = self.A[-1] @ self.W[-1] + self.b[-1]
self.Z.append(z)
self.A.append(z)
return z
def backward(self, y_true, learning_rate=0.01):
m = y_true.shape[0]
dA = mse_deriv(self.A[-1], y_true)
for i in reversed(range(self.num_layers)):
dZ = dA
if i < self.num_layers - 1: # si ce n'est pas la sortie
dZ = dA * tanh_deriv(self.Z[i])
dW = self.A[i].T @ dZ
db = np.sum(dZ, axis=0, keepdims=True)
# Propagation en arrière
dA = dZ @ self.W[i].T
# Mise à jour
self.W[i] -= learning_rate * dW
self.b[i] -= learning_rate * db
def train(self, X, y, epochs=5000, learning_rate=0.01):
for epoch in range(epochs):
y_pred = self.forward(X)
loss = mse_loss(y_pred, y)
self.backward(y, learning_rate)
if epoch % 500 == 0:
print(f"Epoch {epoch}, Loss: {loss:.6f}")
def predict(self, X):
return self.forward(X)
# ====== Expérience : approximation de sin(x) avec tanh ======
# Données
X = np.linspace(0, np.pi, 100).reshape(-1, 1)
y = np.sin(X)
# Modèle : 1 entrée, deux couches cachées de 20 neurones tanh, 1 sortie
model = NeuralNetwork([1, 20, 20, 1])
model.train(X, y, epochs=5000, learning_rate=0.01)
# Prédictions
y_pred = model.predict(X)
# Visualisation
plt.figure(figsize=(8,5))
plt.plot(X, y, label="sin(x)", linewidth=2)
plt.plot(X, y_pred, label="Prédiction NN (tanh)", linestyle="--")
plt.legend()
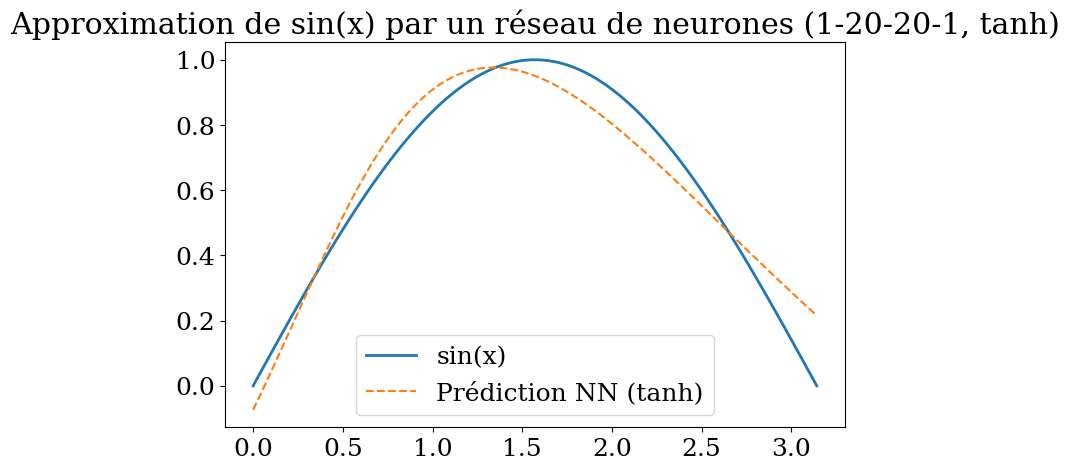
plt.title("Approximation de sin(x) par un réseau de neurones (1-20-20-1, tanh)")
plt.show()
Epoch 0, Loss: 0.074421
Epoch 500, Loss: 0.031877
Epoch 1000, Loss: 0.021896
Epoch 1500, Loss: 0.016829
Epoch 2000, Loss: 0.013954
Epoch 2500, Loss: 0.011969
Epoch 3000, Loss: 0.010382
Epoch 3500, Loss: 0.009038
Epoch 4000, Loss: 0.007881
Epoch 4500, Loss: 0.006882
7.6.5. Bibliothèque scikitlearn#
avec des paramètres optimisés (utilisation « lbfgs » au lieu de « adam »)
from sklearn.neural_network import MLPRegressor
from sklearn.metrics import r2_score
# Données
X = np.linspace(0, np.pi, 100).reshape(-1, 1)
y = np.sin(X)[:,0]
clf = MLPRegressor(max_iter=800, random_state=0, activation='tanh',
solver="lbfgs", verbose=False)
clf = clf.fit(X,y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
y_pred = clf.predict(X)
r2 = r2_score(y, y_pred)
print("R2 score {:.2f}".format(r2))
# Visualisation
plt.figure(figsize=(8,5))
plt.plot(X, y, label="sin(x)", linewidth=2)
plt.plot(X, y_pred, label="Prédiction NN (tanh)", linestyle="--")
plt.legend()
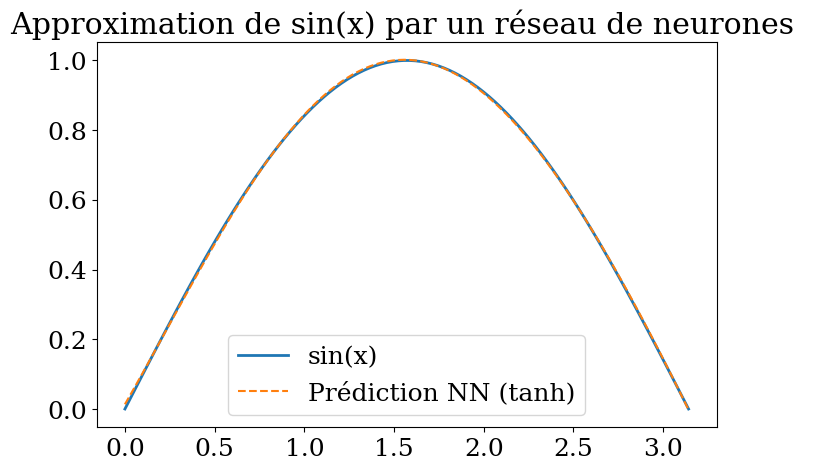
plt.title("Approximation de sin(x) par un réseau de neurones ")
plt.show()
score = 99%
R2 score 1.00
7.6.6. Types de couches#
couche dense: modèle linéaire
couche de type convolution, maxpooling, dropout
couche de type récurrence
Réseaux convolutionnels : traiter la dimension spatiale
Hypothèse : des pixels voisins représentent des choses similaires
Convolution : connexion locale des pixels (voisinage) pour détecter des objets plus gros (lignes/courbes)
Réseaux récurrents : traiter la dimension temporelle
7.7. Réseaux de neurones convolutionnels#
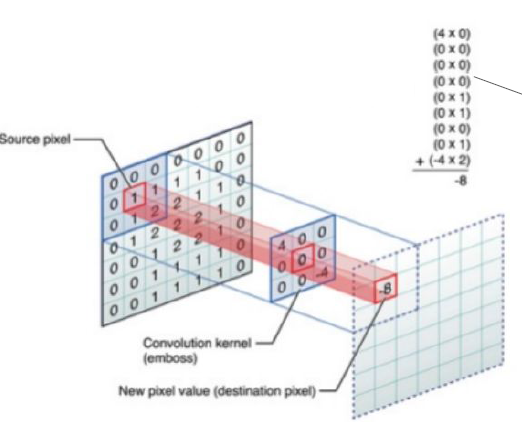
Convolution sur une image
1 filtre 5x5
7.7.1. Type de couches de neurones convolutionnelles#
objectif: réduire la taille des données (image)
\(\Rightarrow\) sur une image, filtre 3x3
Convolution
MaxPooling (remplace plusieurs pixels par le max)
DropOut (élimine des pixels)
7.7.2. classification Neural network#
scikit learn model MLPClassifier
MLP = Multi-layer Perceptron
paramétres:
hidden_layer_sizes = (taille1, taille2)
C’est un Tuple, sa taille représente le nombre de couches et chaque élément représente le nombre de neurones. Si on veut un modèle avec 3 couches de 100 Neurones chacune, on doit mettre :
hidden_layer_sizes = (100,100,100).
Donc la valeur par défaut représente bien une seule couche cachée de 100 Neurones.
from sklearn.neural_network import MLPClassifier
N = 20
X,y,col = dataset3(N)
clf = MLPClassifier(hidden_layer_sizes=(N**2,N**2,N**2), max_iter=400, random_state=1, verbose = False)
clf = clf.fit(X,y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 100%
# prediction
NN = 21
Xpred, ypred, colpred = predict3(NN, clf.predict)
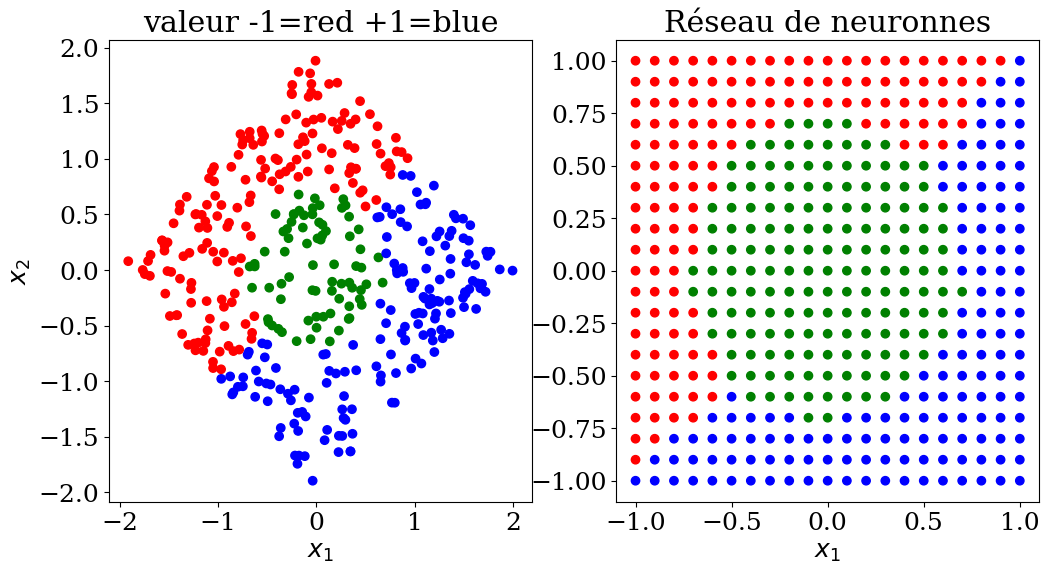
plot3(X,col, Xpred,colpred,titre="Réseau de neuronnes")
7.7.3. regression Neural network#
scikit learn model MLPRegressor
MLP = Multi-layer Perceptron
paramétres:
hidden_layer_sizes = (nbre, taille) 1,2, .. 5
from sklearn.neural_network import MLPRegressor
N = 11
X,y = dataset1(N)
clf = MLPRegressor(hidden_layer_sizes=(N**2,N**2,N**2), max_iter=400, random_state=1, verbose = False)
clf = clf.fit(X,y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
score = 43%
NN = 51
Xpred = np.array([[1,x] for x in np.linspace(1,4,21) ])
ypred = clf.predict(Xpred)
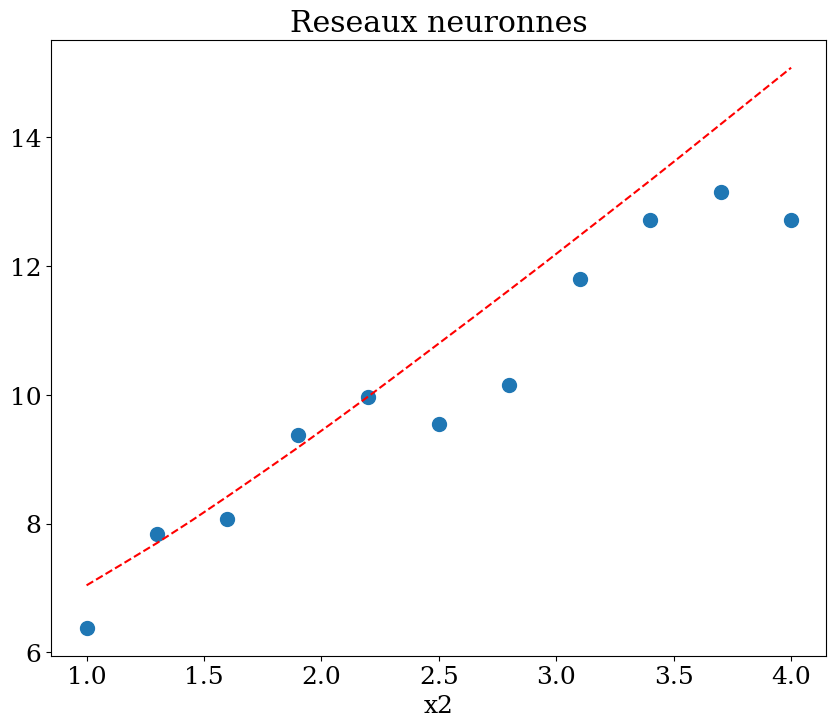
plot1(N,X,y, Xpred,ypred,titre="Reseaux neuronnes")
7.8. Apprentissage avec des séries temporelles#
■ Classification
Identifier les épisodes pluvieux/non pluvieux
Identifier si une station météo est défaillante.
■ Régression
Prédire la température maximale de la journée
Prédire la quantité de pluie attendue
Corriger la température mesurée
■ Problème
définition des données \(X\) (features)
définition des objectifs \(y\) (target)
\(\Rightarrow\) machine learning: trouver le modèle \(f(X)\) minimisant \(L\)
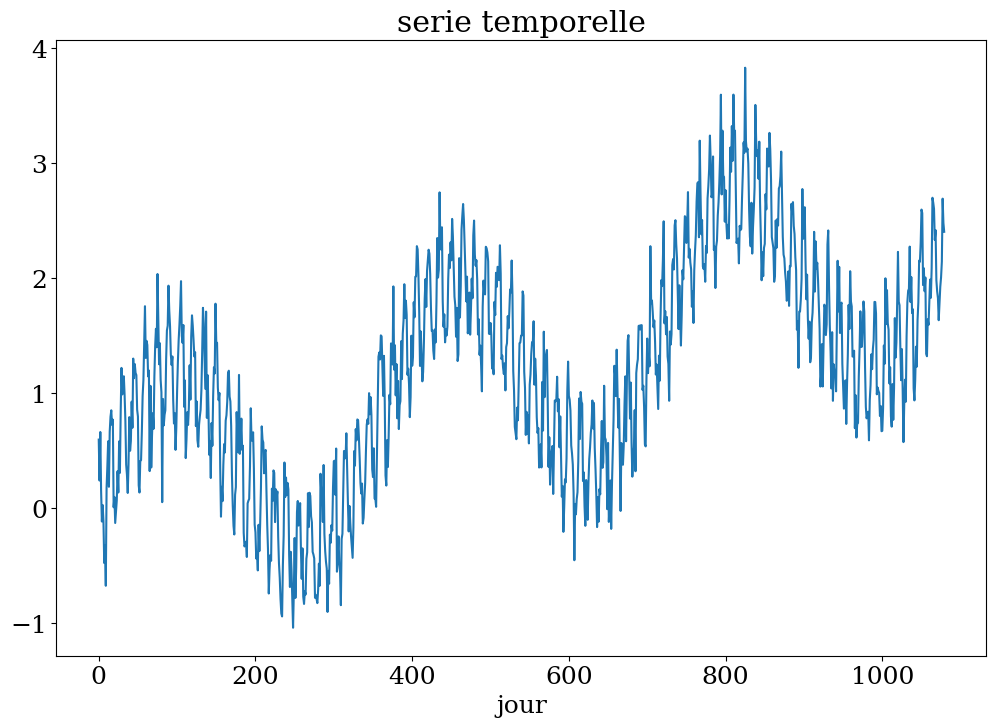
# construction serie
Ts,ys = serie_temp(3)
plt.figure(figsize=(12,8))
plt.plot(Ts[:],ys)
plt.xlabel("jour")
plt.title("serie temporelle");
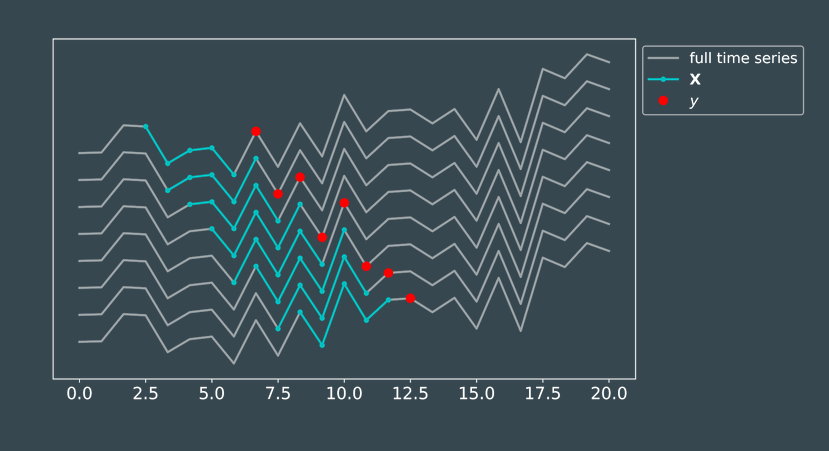
# 50 fenetres de 14 jours pour prediction au jour 300
n = 14
N = 50
t0 = 300
X,y,t = dataset4(Ts,ys,n,N,t0)
plot_data4(n,N,t0,t,X,y,Ts,ys)
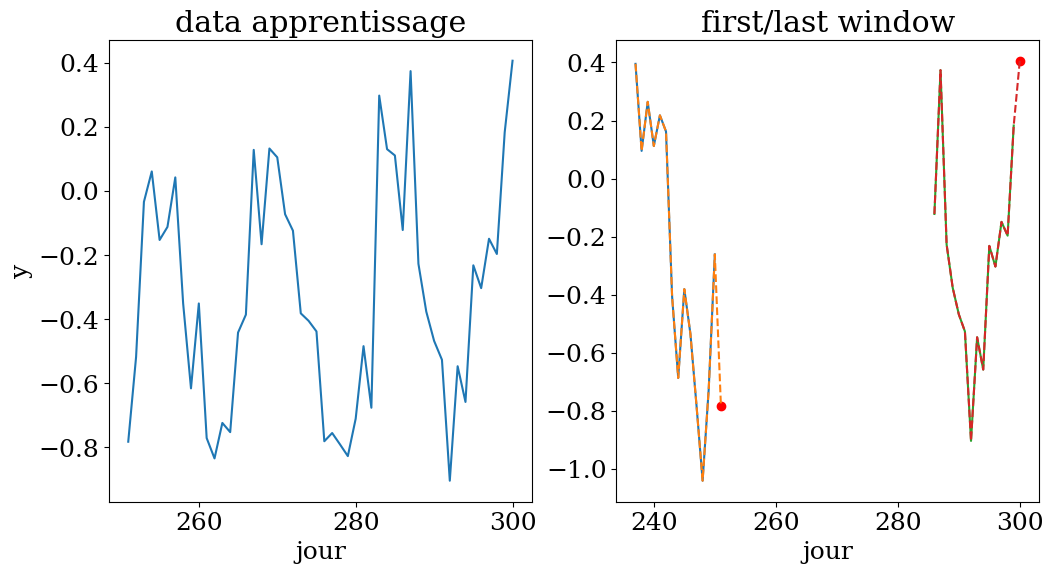
apprentissage sur une fenetre de 14 jours entre le jour 237 et 300
from sklearn.linear_model import LinearRegression
from sklearn.ensemble import RandomForestRegressor
from sklearn.neighbors import KNeighborsRegressor
from sklearn.metrics import r2_score
# choix de l'algorithme
clf = RandomForestRegressor()
#clf = KNeighborsRegressor()
#clf = LinearRegression()
clf.fit(X,y)
print("score = {:2d}%".format(int(100*clf.score(X, y))))
yp = clf.predict(X)
print("R2 = {:3.2f}%".format(r2_score(y,yp)))
score = 92%
R2 = 0.92%
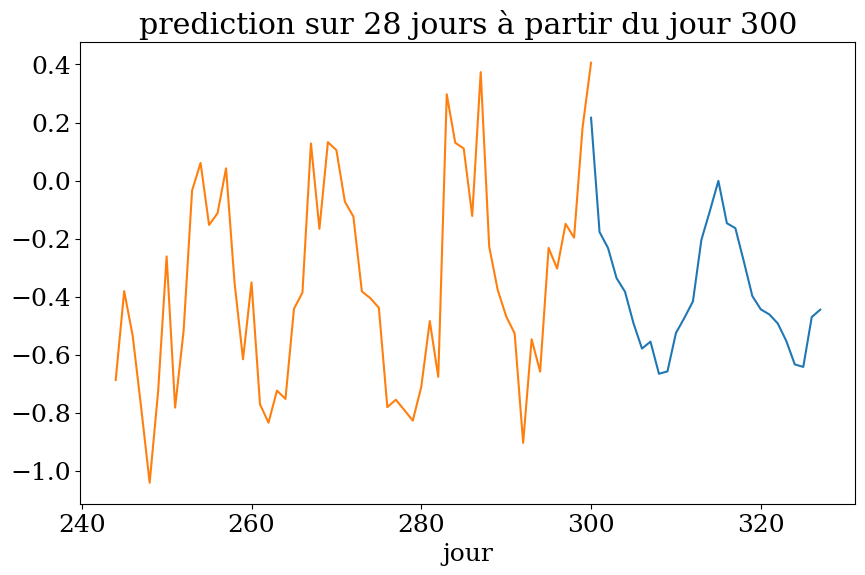
# prediction sur n1 jours
n1 = 2*n
Xpred = np.zeros((n1,n))
ypred = np.zeros(n1)
for k in range(n1):
Xpred[k,:] = ys[t0+k-n:t0+k]
ypred = clf.predict(Xpred)
plot4(n1,t0,Ts,ys,ypred,"prediction")
7.9. Qualité de l’apprentissage#
Métriques de régression pour quantifier la qualité des prédictions
Pour un jeux de tests (# du jeu d’entraînement) de dimension n on évalue l’écart entre la prédiction \(\hat{y}_i\) et la valeur réelle \(y_i\).
Mean squared error MSE
coefficient de détermination: \(R^2\) score
Il représente la proportion de variance (de y) qui a été expliquée par les variables indépendantes du modèle. Il fournit une indication de la qualité de l’ajustement et, par conséquent, une mesure de la manière dont les échantillons invisibles sont susceptibles d’être prédits par le modèle, à travers la proportion de la variance expliquée.
Le meilleur score possible est 1.0
7.10. Conclusion#
Le choix du bon algorithme dépend:
des données
de la connaissance du problème
du choix des paramètres
7.11. Références#
Colin Bernet « L’intelligence artificielle: introduction et applications en physique »
« Formation Deep Learning » de méteo-france
Ricco Rakotomalala, Lyon 2, Cours « DATA MINING et DATA SCIENCE »
Michael Nielsen – Neural Networks and Deep Learning (2015)
Victor Zhou “Neural Networks from Scratch with Numpy”
Emmanuel Franck, INRIA, « Apprentissage et calcul scientifique »
7.12. FIN#
from platform import python_version
print("Python version:",python_version())
print("numpy version:",np.__version__)
print("skit learn version:",sk.__version__)
Python version: 3.10.12
numpy version: 1.26.4
skit learn version: 1.1.3
