Aérodynamique

Contenu

_images/profil_flow.png — Fig. 1 visualisation de l’écoulement autour d’un profil d’aile#

5. Aérodynamique#

L’aérodynamique est une branche de la dynamique des fluides qui étudie les écoulements d’air, et leurs effets sur des éléments solides, en particulier les ailes d’avions ou les pales des éoliennes.

Une aile dans un écoulement (figure Fig. 5.8) peut dans un premier temps être étudiée en 2D (figure Fig. 5.9). La théorie des profils mince (voir l’article sur wikipedia) permet d’expliquer l’apparition de la force portance sur un profil mince dans un écoulement en utilisant une théorie de fluide parfait avec circulation de vitesse.

_images/profil3D.png — Fig. 5.8 profil d’aile en 3D#

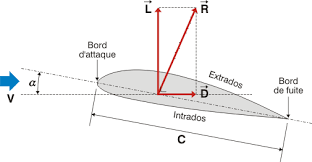
_images/profil2D.png — Fig. 5.9 profil d’aile en 2D#

La forme du profil permet en effet de créer une circulation de vitesse autour du profil (dans le sens des aiguilles d’une montre). Cette circulation va accélérer la vitesse sur l’extrados (partie supérieure de l’aile) et au contraire diminuer la vitesse sur l’intrados (partie inférieure).

En utilisant Bernoulli, on a donc une dépression sur l’extrados et une surpression sur l’intrados, ce qui génère une force de portance $F_p$ (noté L pour lift sur le schéma) perpendiculaire à la direction de la vitesse incidente (donc ici dans la direction verticale).

La répartition de pression engendre aussi une force de traînée dans la direction horizontale, dite traînée de forme. Alors que la force de portance est bien prédite par la théorie fluide parfait des profils minces, la force de traînée $F_t$ ( noté D pour drag sur le schéma) est elle essentiellement d’origine visqueuse. La théorie précédente n’est donc pas suffisante pour la prédire. Il faut utiliser la théorie de la couche limite pour espérer la prédire correctement.

Lorsque l’angle d’incidence augmente et dépasse une valeur limite, la couche limite sur l’extrados décolle et le profil décroche avec une apparition de tourbillon et une perte soudaine de portance (voir image ci dessous de l’expérience de Prandtl).

On limitera donc l’étude à des angles d’incidence compris entre -20° et +20°.

_images/decrochage.jpg — Fig. 5.10 visualisation du décrochage d’une aile#

5.1. Analyse dimensionnelle#

On considère un profil de corde $L_c$ (noté C sur la figure) et d’envergure $W$ avec une incidente $\alpha$ par rapport à une vitesse amont horizontale $U_0$. Le fluide est de l’air de viscosité $\mu$ et de masse volumique $\rho_0$. On veux calculer les composantes de la force aérodynamique $\vec{F_a}$

\[ \vec{F_a} = F_p \vec{e_y} - F_t \vec{e_x}\]

Le problème étudié dépend donc 3 unités de base (m/s/kg) et de 8 grandeurs:

\[ F_p, F_t, U_0, \rho, \mu, \alpha, L_c, W \]

avec lesquelles on construit 5 nombres sans dimensions

l’angle d’incidence $\alpha$, en générale petit (de -20° et +20° )
l’élancement de l’aile, rapport de l’envergure sur la corde, qui est très grand pour les planeurs, un peu moins pour les avions de lignes et peit pour les avions de chasse

\[ \Phi = \frac{W}{L_c}\]

le nombre de Reynolds: $Re$, en générale très grand vu la vitesse de vol des avions

\[Re=\frac{\rho CV}{\mu}\]

le coefficient de portance $C_L$

\[C_L=\frac{F_{L}}{\frac{1}{2}\rho V^{2}L_C W}\]

le coefficient de traînée $C_D$

\[C_D=\frac{F_{D}}{\frac{1}{2}\rho V^{2}L_C W}\]

La loi sur la portance s’écrit alors sous forme sans dimension:

\[ C_L = \frac{F_p}{\frac{1}{2}\rho_0 U_0^2 L_c W} = C_L(\alpha, Re, \Phi)\]

et la loi de traînée

\[ C_D = \frac{F_t}{\frac{1}{2}\rho_0 U_0^2 L_c W} = C_D(\alpha, Re, \Phi) \]

5.2. Théorie simplifiée de la portance#

On présente ici un modèle simplifié des efforts exercés par un profil d’aile de longueur (de corde) $L_c$ en incidence d’angle $\alpha$ sur un écoulement stationnaire d’un fluide parfait incompressible de masse volumique $\rho$ et de vitesse $U_1$ (schéma ci-dessous Fig. 5.11). Ce présentation est inspirée de l’article de H. Babinsky « How do wings work? » [1]

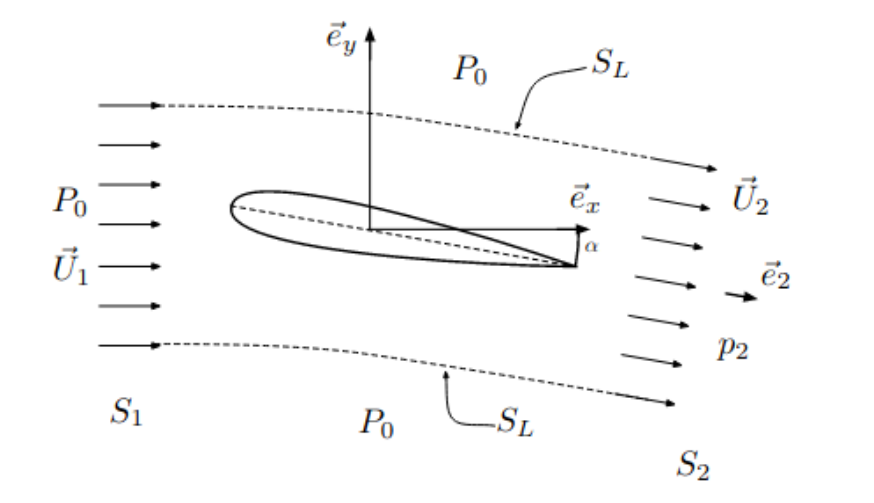
_images/portance_aile1.png — Fig. 5.11 schéma de l’écoulement autour d’un profil d’aile#

On constate expérimentalement (figure Fig. 5.12) que l’effet de l’aile sur l’écoulement, aux faibles incidences, est de dévier les lignes de courant d’un angle $\alpha$ correspondant à l’angle d’incidence du profil, c.a.d l’angle d’inclinaison du bord de fuite. Sur cette figure, on note que la déviation de l’écoulement est régulière uniquement aux faibles incidences (pour des angles $\alpha$ jusqu’à une vingtaine de degrés), et qu’à forte incidence l’écoulement à l’arrière de l’aile devient très complexe (sillage turbulent).

_images/aile_lignecourant1.png — Fig. 5.12 visualisation expérimentale de l’écoulement autour d’un profil d’aile#

D’après le principe fondamental de la dynamique, un changement de direction de la quantité de mouvement d’un système est forcément du à l’application d’une force extérieure. Le profil exerce donc une force sur l’écoulement pour le dévier, et par principe d’action-réaction l’écoulement exerce une force opposée $\vec{F}$ sur le profil.

Cette force aérodynamique $\vec{F}$:

\[\vec{F} = F_x \vec{e}_x + F_y \vec{e}_y\]

qui possède 2 composantes:

une composante horizontale $F_x$ parallèle à la direction de l’écoulement amont, que l’on appelle la force de traînée, et qui s’oppose à l’avancement de l’avion,
une composante verticale $F_y$ perpendiculaire à la direction de l’écoulement amont, que l’on appelle la force portance, qui permet aux avions de voler

Pour déterminer cette force, on va effectuer des bilans dans un volume de contrôle $\Omega$ limité par une surface amont $S_1$, une surface avale $S_2$ et une surface latérale $S_L$ (figure Fig. 1). On suppose qu’en $S_1$ la vitesse moyenne est horizontale, vaut $U_1$ et est perpendiculaire à $S_1$, qu’en $S_2$ la vitesse moyenne est inclinée d’un angle $\alpha$, vaut $U_2$ et est perpendiculaire à $S_2$, et que sur la surface $S_L$ la vitesse est tangente à $S_L$.

L’écoulement étant incompressible, le bilan des flux de masse est donc nulle à travers la surface de $\Omega$. La surface $S_l$ étant parallèle à la vitesse (ligne de courant), le flux de masse à travers cette surface est nulle. On en déduit l’égalité entre le flux de masse entrant à travers $S_1$ et le flux de masse sortant à travers $S_2$:

(5.1)#\[ \rho U_1 S_1 = \rho U_2 S_2 \Rightarrow U_1 S_1 = U_2 S_2 \]

On suppose que les surfaces $S_1$, $S_2$, $S_L$ sont suffisamment loin du profil, pour que la pression sur ces surfaces reste quasiment égale à $p_0$ (on a donc $p_2=p_0$).

Avertissement

Ce n’est pas parce que la pression est constante sur la frontière de $\Omega$ que la pression $p$ est constante dans le volume de contrôle de contrôle.

En négligeant les forces de viscosité, la force $\vec{F}$ exercée par l’écoulement sur le profil correspond essentiellement à la résultant des forces de pression sur le profil.

L’écoulement étant stationnaire et en négligeant les effets de viscosité, on peut utiliser le théorème de Bernoulli entre l’entrée et la sortie le long de la surface $S_L$ qui est une ligne (surface) de courant.

\[p_1 + \frac{1}{2} \rho U_1 ^2 = p_2 + \frac{1}{2} \rho U_2 ^2\]

Avec l’hypothèse $p_1=p_2=p_0$ on en déduit l’égalité des modules des vitesses, et donc des surfaces $S_1$ et $S_2$ d’après (5.1):

\[ U_1 = U_2 \mbox{ et } S_1 = S_2\]

On constate expérimentalement qu’à l’arrière du profil, la zone de déflexion de l’écoulement est de l’ordre de grandeur de la longueur de la corde $L_c$. On peut donc estimer la surface $S_2$ comme $S_2=W L_c$ où $W$ est l’envergure de l’aile dans la direction perpendiculaire au plan $Oz$. On va maintenant pouvoir utiliser le bilan de quantité de mouvement pour calculer $\vec F$:

le flux de quantité de mouvement à travers $S_L$ est nul car la vitesse est tangente à $S_L$
le flux de quantité de mouvement en entrée à travers $S_1$ vaut: $$ -\rho U_1^2 S_1 \vec{e_x}$$
le flux de quantité de mouvement en sortie à travers $S_2$ vaut: $$ \rho U_2^2 S_2 (\cos\alpha\,\vec{e_x} - \sin\alpha\,\vec{e_y})$$
la pression étant constante sur toutes les frontières de $\Omega$, la résultante des forces de pression sur ces frontières fermées est donc nulle

Le bilan de quantité de mouvement s’écrit donc

(5.2)#\[\begin{eqnarray} -\rho U_1^2 S_1 \vec{e_x} + \rho U_2^2 S_2 (\cos\alpha\,\vec{e_x} - \sin\alpha\,\vec{e_y}) &=& -\vec{F} \\ &=& -F_x \vec{e_x} - F_y \vec{e_y} \end{eqnarray}\]

En utilisant les résultats précédents, on en déduit l’expression de $F_x$ et $F_y$ en fonction des paramètres du problème:

\[ F_x \approx \rho U_1^2 L_c W (1-\cos\alpha) \mbox{ et } F_y \approx \rho U_1^2 L_c W\, \sin\alpha \]

En supposant l’angle $\alpha$ petit, on peut en déduire la force de traînée $F_D$ est négligeable et que la force de portance $F_L$ vaut:

\[ F_D=F_x \approx 0 \mbox{ et } F_p = F_y \approx \rho \alpha U_1^2 L_c W \]

d’où le coefficient de portance $C_L$

\[ C_L = \frac{F_p}{1/2 \rho U_1^2 L_c W} \approx 2 \alpha \]

Cette théorie simplifiée permet de montrer que la portance d’une aile est bien proportionnelle à l’angle d’incidence et à la longueur de la corde, ce qui est constaté expérimentalement. Par contre la forme du profil n’intervient pas dans l’analyse. Or expérimentalement la forme du profil d’aile joue un rôle fondamentale dans la valeur de la portance.

Pour prendre en compte la forme du profil, il faut faire appel à une théorie plus complexe: la théorie des potentielles complexes et des transformations conformes de Kutta-Joukovski, qui est détaillé dans le notebook suivant.