4. Analyse dimensionnelle#

4.1. Propriétés des lois physiques#

En physique classique, les lois sont indépendantes du système de mesures et doivent vérifier des propriétés homogénéité:

  • Toute relation entre grandeurs physiques est indépendante du système d’unités de mesure

  • Toute relation entre des grandeurs physiques est dimensionnellement homogène

Note

on doit systématiquement vérifier l’homogénéité dimensionnelle des formules

En Mécanique des fluides (hors électromagnétisme) le système d’unité utilisé est basée sur

  • 4 grandeurs fondamentales sont : Longueur \(L\), masse \(M\), temps \(\tau\) et température \(T\)

  • les unités fondamentales en Mécanique sont donc: longueur \(L\), masse \(M\), temps \(\tau\) et température \(T\), soit en unité SI: \(m,\,kg\,,s\,,K\)

  • les autres unités sont des unités dérivées:

exemple: force en Newton = masse x accélération et donc \(N=kg\,m\,s^{-2}\)

4.2. Analyse dimensionnelle#

4.2.1. Nombre sans dimension#

En mécanique des fluides, interviennent couramment des nombres sans dimension, en particulier pour les études par similitude sur des modèles réduits

Une grandeur sans dimension ou adimensionnelle est un produit de grandeurs physiques dont la dimension vaut 1, ce qui revient à dire que tous ses exposants dimensionnels sont nuls

nbre sans dimension \(\Pi\) tq. \(dim(\Pi)=L^0 M^0 \tau^0 T^0 = 1\)

Un des nombres sans dimension le plus connu en mécanique des fluides est nombre de Reynolds :

\[Re=\frac{\rho UL}{\mu}\]

Ce nombre traduit le rapport des termes de convection \(\rho U\frac{\partial U}{\partial x}\approx\rho\frac{U^{2}}{L}\) sur les termes de viscosité \(\mu\frac{\partial^{2}U}{\partial x^{2}}\approx\mu\frac{U}{L^{2}}\) dans les équations de Navier-Stokes.

L’intérêt des nombres sans dimension

Les nombres sans dimension interviennent pour

  • la modélisations (choix des termes importants)

  • les expériences à échelle réduite

  • l’étude des lois de similitude

4.3. Théorème de Vaschy-Buckingham#

C’est un des théorèmes de base de l’analyse dimensionnelle, appelé aussi théorème Pi .

Théorème Pi

Ce théorème établit que si une équation physique met en jeu \(n\) variables physiques, celles-ci dépendant de \(k\) unités fondamentales, alors il existe une équation équivalente mettant en jeu \(pn − k\) variables sans dimension construites à partir des variables originelles.

Soit une loi physique dépendant de n des quantités physiques \(a_{1},a_{2},a_{3},..a_{n}\):

\[f(a_{1},a_{2},a_{3},..a_{n})=0\]

Si les \(n\) variable physiques \(\{a_{i}\}\) s’expriment en fonction de \(k\) unités fondamentales indépendantes, alors la loi précédente peut s’écrire en fonction de \(p=n-k\) nombres sans dimension:

\[F(\pi_{1},\pi_{2}..\pi_{p})=0\mbox{ avec }p=n-k\]

où les \(\pi_{i}\) sont \(p\) paramétrés sans dimension construit à partir des \(a_{i}\)

\[\pi_{i}=a_{1}^{\alpha_{1}^{i}}a_{2}^{\alpha_{2}^{i}}..a_{n}^{\alpha_{n}^{i}}\]

4.3.1. cas d’un écoulement général#

Soit un écoulement de fluide défini par les \(n=10\) grandeurs suivantes

  • \(U_{0}\) échelle de vitesse,

  • \(c_{0}\)vitesse caractéristique du son (\(c_{0}=\sqrt{\gamma RT_{0}}\)),

  • \(\rho_{0}\) masse volumique caractéristique

  • \(L\) échelle de longueur,

  • \(\tau_{0}\) échelle de temps (instationnaire)

  • 5 paramètres physiques \(g\) \(\mu\)\(\lambda\) \(C_{p}\) \(C_{v}\)

Ces 10 grandeurs dépendent de \(k=5\) unités fondamentales

  • 4 unités fondamentales \(m/kg/s/K\)

Cela permet de définir \(p=6\) nombres sans dimension.

Ces nombres sont les nombres sans dimension classiques en mécanique des fluide:

  1. Strouhal: \(S_{t}=\frac{U_{0}\tau_{0}}{L}\) est le nombre de Strouhal qui mesure l’importance relative des termes de convections sur le terme instationnaire

  2. Reynolds\(Re=\frac{\rho_{0}U_{0}L}{\mu}\) est le nombre de Reynolds qui mesure l’importance relative des vitesses de convection et de diffusion visqueuse.

  3. Froude \(Fr=\frac{U_{0}}{\sqrt{Lg}}\) est le nombre de Froude qui mesure l’importance relative des forces d’inerties et de pesanteur

  4. Mach \(Ma=\frac{U_{0}}{c_{0}}\) est le nombre de Mach, qui mesure les effets de compressibilité.

  5. Pechlet \(Pe=\frac{\rho_{0}C_{p}U_{0}L}{\lambda}\) le nombre de Pechlet qui mesure l’importance relative de la convection et de la diffusion de la chaleur. On peut le remplacer par le nombre de Prandtl \(Pr=\frac{C_{p}\mu}{\lambda}\) t.q. \(Pe=Re\,Pr\))

  6. constante thermodynamique \(\gamma=\frac{C_{p}}{C_{v}}\)

4.3.2. cas d’un écoulement autour d’un profil#

On veut déterminer la force de portance \(F_L\) générée par un écoulement de fluide incompressible de vitesse \(V\), de masse volumique \(\rho\) et de viscosité \(\mu\) autour d’un profil en incidence d’angle \(\alpha\) et de longueur de corde \(C\). L’écoulement est supposée 2D et la portance est définie par unité de longueur transverse. On cherche la relation entre la force de portance et les autres paramètres:

\[ F_L = F(\rho,\mu,V,C,\alpha)\]
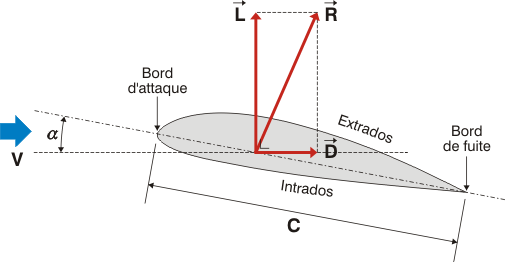
_images/profil.png

Fig. 4.1 écoulement autour d’un profil#

Les 6 grandeurs du problème pour la portance \(F_{L}\) par unité de longueur, la vitesse \(V\), l’angle \(\alpha\), longueur de corde \(C\), la masse volumique du fluide \(\rho\) et sa viscosité \(\mu\)

Avec 6 grandeurs physiques et 3 unités fondamentales \((m,kg,s)\), on définit 3 nombres sans dimension

  1. l’angle \(\alpha\)

  2. le nombre de Reynolds: \(Re=\frac{\rho CV}{\mu}\)

  3. le coefficient de portance \(c_L=\frac{F_{L}}{\frac{1}{2}\rho V^{2}C}\),

La loi sur la portance s’écrit alors sous forme sans dimension:

  • loi sans dimension sur la portance

    \[c_{L}=c_{L}(Re,\alpha)\]

qui est la forme sans dimension classique de la portance pour un profil d’aile.

Une analyse identique sur la force de traînée, conduit à la forme sans dimension classique de la traînée donnée par le coefficient de trainée \(c_D\)

4.4. Perte de charge#

Le calcul des pertes de charges dans les réseaux de conduite d’alimentation en eau est une application des nombres sans dimension, qui permet le dimensionnement des pompes en utilisant une analyse globale des écoulements.

4.4.1. cas d’un écoulement dans un tuyau#

On considère un écoulement d’un fluide pesant incompressible de vitesse \(U80\), de masse volumique \(\rho\), de viscosité \(\mu\) dans un tuyau de longueur \(L\), de diamètre \(D\). On observe une différence de pression \(\Delta p\) entre l’entrée et la sortie, qui sont distants en hauteur de \(H\). On nore \(g\) l’accélération de la pesanteur. On veut déterminer la loi donnant la perte de charge \(\Delta p\) en fonction des autres paramètres.

Les 8 paramètres du problèmes sont: `

  • 3 paramètres géométriques: \(L,H,D\)

  • 3 propriétés physiques: \(\rho,\,\mu,\,g\)

  • 2 paramètres de l’écoulement: \(U_{0}\), \(\Delta p\)

Avec 8 grandeurs et 3 unités \((m,kg,s)\), on définit donc 5 nombres sans dimension

  1. Reynolds \(Re=\dfrac{\rho U_{0}D}{\mu}\)

  2. Froude \(Fr=\dfrac{U_{0}}{\sqrt{gH}}\)

  3. 1er rapport de longueur \(\alpha=\dfrac{H}{L}\)

  4. 2nd rapport de longueur \(\beta=\dfrac{D}{L}\)

  5. le coefficient de perte de charge \(K = \dfrac{\Delta p}{\frac{1}{2} \rho U_0^2}\)

La loi sans dimension sur \(K\) s’écrit:

\[ K = K(Re,Fr,\alpha,\beta)\]

qui permet de calculer la puissance hydraulique \(P\) (i.e. la puissance de la pompe) nécessaire pour assurer une vitesse de débit \(U_0\) donnée:

\[ P = \Delta p.\pi\frac{D^{2}}{4}.U0=\frac{\pi}{8} K\rho U_{0}^{3}D^{2}\]

4.4.2. calcul de perte de charge#

La perte de charge correspond à la dissipation, par frottements, de l’énergie mécanique du fluide en mouvement dans un tuyau. Pour un écoulement stationnaire d’un fluide incompressible sans transfert de chaleur, les paramètres du problème sont la vitesse moyenne \(U\), le diamètre \(D\) et la longueur \(L\) de la conduite, la masse volumique \(\rho\) et la viscosité \(\mu\) du fluide, et enfin la différence de pression \(\Delta p\) entre l’entrée et la sortie.

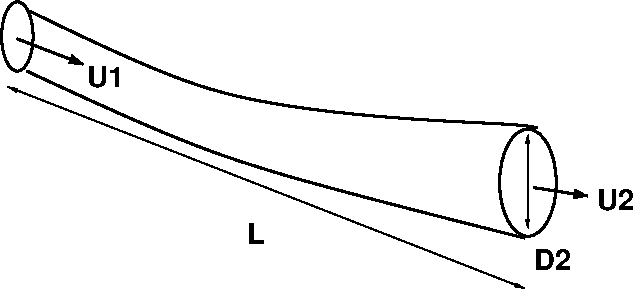
_images/tuyau.png

Fig. 4.2 écoulement dans un tuyau#

L’analyse dimensionnelle pour ce problème à 6 paramètres conduit à la relation

\[ K = K(Re,\alpha)\]

entre les 3 nombres sans dimension du problème:

  1. le nombre de Reynolds \(Re=\frac{\rho U D}{\mu}\)

  2. le rapport de longueur \(\alpha=\frac{D}{L}\)

  3. le coefficient de perte de charge \(K = \frac{\Delta p}{\frac{1}{2}\rho U^2}\)

Dans le cas d’un écoulement établie laminaire, le champ de vitesse dans la conduite est parabolique (profil de Poiseuille):

\[ U(r) = U_{max} (1-\left(\frac{2r}{D}\right)^{2})\]

et la vitesse moyenne \(U\) vaut \(U=U_{max}/2\).

L’application du bilan globale de quantité de mouvement entre l’entrée et la sortie conduit à la relation

\[ \Delta p \frac{\pi D^2}{4} + \int_{x=0}^L \tau_w \pi D dx =0\]

où \(\tau_{w}\) représente le frottement à la paroi due au cisaillement

\[\tau_{w}=\mu\frac{\partial U}{\partial r}\mid_{w} = -\mu\frac{4 U_{max}}{D}\]

D’où

\[ \Delta p \frac{\pi D^2}{4} = \mu\frac{4 U_{max}}{D} \pi D L \]

ce qui conduit à l’expression classique de la perte de charge dans un tuyau cylindrique en écoulement laminaire (\(Re<2000\))

\[ \Delta p = \frac{1}{2} U^2 K \mbox{ avec } K = \frac{L}{D} \frac{64}{Re} \]

Pour un écoulement turbulent en conduite lisse (\(3000<R_{e}<10^{5}\)), l’approximation de Blasius pour le champ de vitesse moyen:

\[\frac{U(r)}{U_{max}}=\left(1-\frac{2r}{D}\right)^{\frac{1}{7}}\]

permet d’obtenir l’approximation de \(K\) suivante:

\[ K = \frac{L}{D} 0.316\,R_{e}^{-0.25}\]

Dans le cas général, avec des élargissements brusques, clapets, vannes, coudes, .., la détermination du coefficient de perte de charge \(K\) est principalement du domaine de l’expérience, et on a recours à des données semi empiriques (abaques).