Lois de bilan globales en stationnaire

Contenu

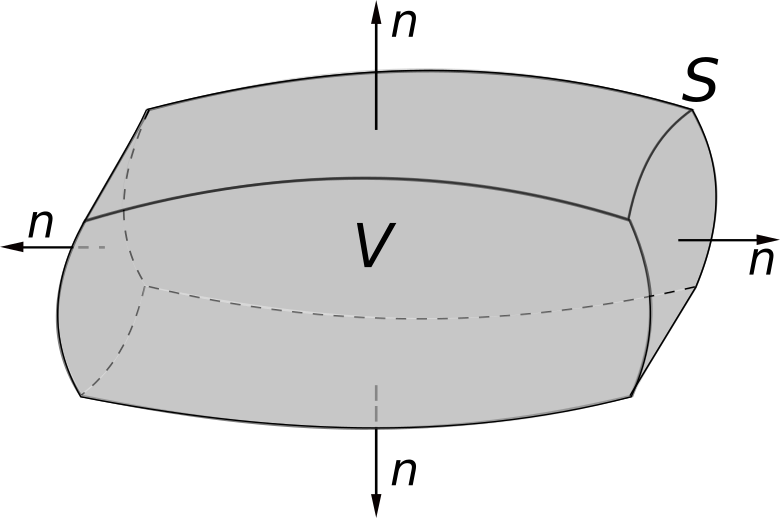
3. Lois de bilan globales en stationnaire#

L’objectif de cette partie est d’obtenir une information globale sur écoulement de fluide dans un domaine $\Omega$ en utilisant:

un bilan global
une approche moyenne
sans connaître le détail de l’écoulement
c’est une première approximation

Applications: conception 0D de systèmes complexes

3.1. Équations locales#

On part de la forme conservative des équation locales, écrites dans un repère cartésien $(x,y,z)$

bilan de masse

\[\frac{\partial\rho}{\partial t}+div(\rho\overrightarrow{U})=0\]

bilan de quantité de mouvement (suivant x, y et z)

en notant $\overrightarrow{F_{\mu}} = div(\mu \overline{\overline{\sigma}}_v\overrightarrow{U})$ le bilan des forces de viscosité

\[\begin{split}\begin{aligned} \frac{\partial\rho u}{\partial t}+div(\rho u\overrightarrow{U}) & +\overrightarrow{grad}\,p.\overrightarrow{e_{x}}=(\rho\overrightarrow{g}+\overrightarrow{F_{\mu}}).\overrightarrow{e_{x}}\\ \frac{\partial\rho v}{\partial t}+div(\rho v\overrightarrow{U}) & +\overrightarrow{grad}\,p.\overrightarrow{e_{y}}=(\rho\overrightarrow{g}+\overrightarrow{F_{\mu}}).\overrightarrow{e_{y}}\\ \frac{\partial\rho w}{\partial t}+div(\rho w\overrightarrow{U}) & +\overrightarrow{grad}\,p.\overrightarrow{e_{z}}=(\rho\overrightarrow{g}+\overrightarrow{F_{\mu}}).\overrightarrow{e_{z}}\\ \end{aligned}\end{split}\]

bilan d’énergie

\[\begin{split}\begin{aligned} \frac{\partial\rho e_{t}}{\partial t}+div(\rho h_{t}\overrightarrow{U}) & =\delta W+\delta Q\\ \end{aligned}\end{split}\]

relations thermodynamiques

\[e=\frac{1}{\gamma-1}\frac{p}{\rho}\mbox{ et }e_{t}=e+\frac{1}{2}U^{2},\,\,h_{t}=e_{t}+\frac{p}{\rho}\]

3.2. Équations de Navier-Stokes sous forme symbolique#

Ce système d’équation peut s’écrire sous forme symbolique:

\[\frac{\partial W_{i}}{\partial t}+div(\overrightarrow{F_{i}}(\overrightarrow{W}))=div(\overrightarrow{G_{i}}(\overrightarrow{W}))+S_{i}\]

où

$\overrightarrow{W}=\left[\begin{array}{ccccc} \rho & \rho u & \rho v & \rho w & \rho(e+\frac{1}{2}U^{2})\end{array}\right]$ est le vecteur d’état,
$F_{i}(\overrightarrow{W})$ est le vecteur flux convectif (+ pression) associé:

\[\begin{split}\overrightarrow{F}_{\rho}=\left[\begin{array}{c} \rho u\\ \rho v\\ \rho w \end{array}\right],\,\overrightarrow{F}_{u}=\left[\begin{array}{c} \rho u^{2}+p\\ \rho uv\\ \rho uw \end{array}\right],\,\overrightarrow{F}_{v}=\left[\begin{array}{c} \rho uv\\ \rho v^{2}+p\\ \rho vw \end{array}\right],\,\overrightarrow{F}_{h_{t}}=\left[\begin{array}{c} \rho uh_{t}\\ \rho vh_{t}\\ \rho wh_{t} \end{array}\right]\end{split}\]

$\overrightarrow{G_{i}}(\overrightarrow{W})$ est le vecteur des flux diffusifs (forces surfaciques liées à la viscosité)
$S_{i}$ représente le bilan des termes sources (gravité)

On va maintenant intégrer ces équations dans le domaine $\Omega$ en utilisant le Thèoréme de la divergence (Green-Ostrogradski)

3.2.1. théoréme de la divergence#

ce théorème d’analyse vectorielle permet de transformer l’intégrale de la divergence d’un vecteur $\overrightarrow{F}$ dans un domaine $V$ en une intégrale de flux sur la frontière $S$ du domaine avec une normale orientée vers l’extérieure

_images/Divergence_theorem.png — Fig. 3.1 domaine V et frontière S#

\[\iiint_{V}div(\overrightarrow{F})\,dV=\iint_{S=\partial V}\overrightarrow{F}.\overrightarrow{n}\,dS\]

3.2.2. Intégration en stationnaire#

Si on suppose l’écoulement stationnaire, en utilisant le théorème précédent l’intégration dans un volume de fluide $\Omega,$ de frontière $\Gamma=\partial\Omega$ des équations de Navier Stokes sous forme formelle s’écrit:

\[ \underbrace{\int_{\Gamma}\overrightarrow{F_{i}}(\overrightarrow{W}).\overrightarrow{n}\,ds}_{flux\,convectifs+pression} \,=\,\underbrace{\int_{\Gamma}\overrightarrow{G_{i}}(\overrightarrow{W}).\overrightarrow{n}\,ds}_{flux\,diffusifs} +\underbrace{\int_{\Omega}S_{i}dv}_{terme\,source} \]

Cette équation ne fait apparaître que les valeurs des variables d’état $\overrightarrow{W}$ sur la frontière, ainsi que les termes sources dans le domaine.

On pourrait donc penser que cette relation ne fait pas intervenir la valeur de l’état dans le domaine, et donc que l’on a pas à résoudre les équations de Navier-Stokes pour l’utiliser.

Malheureusement, dues aux fortes non linéarité, l’état sur la frontière dépends de l’état à l’intérieur.

Par contre, il est en générale plus simple de faire des approximations sur l’état sur la frontière, ce qui va nous permettre de déterminer des relations entre ce qui rentre dans le domaine et ce qui en sort, et ainsi obtenir des premières estimations, qui serviront ensuite pour analyser l’écoulement et faire si nécessaire une étude plus précise.

3.2.3. Système conservatif#

Si on suppose que les termes sources et les fluxs diffusifs sont négligeables, alors on a conservation des flux convectifs et de pression $\overrightarrow{F}(\overrightarrow{W})$

\[ \int_{\Gamma}\overrightarrow{F_{i}}(\overrightarrow{W}).\overrightarrow{n}\,ds = 0\]

soit :

$\overrightarrow{F}_{\rho}$ = le flux de masse
$\overrightarrow{F}_{u}$ le flux de quantité de mouvement suivant x avec la composante de pression suivant x
$\overrightarrow{F}_{v}$ le flux de quantité de mouvement suivant y avec la composante de pression suivant y
$\overrightarrow{F}_{w}$ le flux de quantité de mouvement suivant z avec la composante de pression suivant z
$\overrightarrow{F}_{h_t}$ = le flux d’enthalpie total $h_t = e +\frac{1}{2}U^{2}$

Les variables $\overrightarrow{W}$ sont appeléés variables conservatives $\overrightarrow{W}=\left[\begin{array}{ccccc} \rho & \rho u & \rho v & \rho w & \rho(e+\frac{1}{2}U^{2})\end{array}\right]$

3.3. Applications#

Considérons le domaine de contrôle suivant avec un entrée (1) horizontale de vitesse moyenne $U_1$ et une sortie (2) verticale de vitesse moyenne $U_2$, qui est dessiné sur la figure ci-dessous:

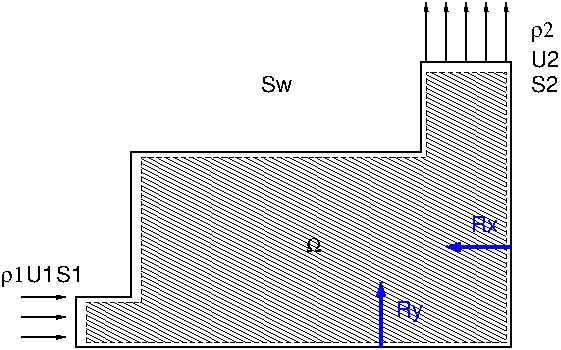
_images/controle1.png — Fig. 3.2 domaine de contrôle#

3.3.1. Bilan de la masse#

Pour un écoulement stationnaire,

le flux de masse globale est nul à travers n’importe quelle surface fermée

\[div(\rho\overrightarrow{U})=0\,\,\,\,\leadsto\,\,\,\int_{S}\rho\overrightarrow{U}.\overrightarrow{n}\,dS=0\]

Pour ce domaine, en notant $S_{1}$ la section d’entrée, $S_{2}$ la section de sortie , $S_{W}$ les parois solides où on a une condition d’adhérence: $\overrightarrow{U}=0$

En raisonnant sur des quantités moyennes, en remplaçant les intégrales dans une section par la valeur moyenne fois la section, et en approximant la moyenne du produit par le produit des moyennes: $$\int_{S_1} \rho\overrightarrow{U}.\overrightarrow{n}\,dS = - \overline{\rho_1 U_1} S_1 \approx -\rho_{1}U_{1}S_{1}$$

le bilan de masse s’écrit en fonction des valeurs moyennes entrantes $\rho_1$,$U_1$ et des sortantes $\rho_{2}$,$U_{2}, on a:

\[-\rho_{1}U_{1}S_{1}+\rho_{2}U_{2}S_{2}=0\]

Note

Cette relation traduit la conservation de la masse pour un écoulement stationnaire:

le débit massique entrant est égale au débit massique sortant.

3.3.2. Bilan de quantité de mouvement#

Pour un écoulement stationnaire,

le flux de quantité de mouvement et de pression $\rho\overrightarrow{U}\otimes\overrightarrow{U}+p\,\overline{\overline{Id}}$ à travers n’importe quelle surface fermée est égale à la résultante $\overrightarrow{R_w}$ des forces de viscosité exercées sur la surface et des forces de volume $\overrightarrow{F_v}$:

\[\int_{S}(\rho\overrightarrow{U}\otimes\overrightarrow{U}).\overrightarrow{n}dS+\int_{S}p\overrightarrow{n}\,dS=\int_{S}\overline{\overline{\sigma}}_{v}\otimes\overrightarrow{n}\,dS+\overrightarrow{F_v}\]

Pour la configuration étudiée on a $\overrightarrow{F_v}=0$

\[\underbrace{\int_{S_{1}}(\rho_{1}\overrightarrow{U_{1}}\otimes\overrightarrow{U_{1}}).\overrightarrow{n}dS+\int_{S_{2}}(\rho_{2}\overrightarrow{U_{2}}\otimes\overrightarrow{U_{2}}).\overrightarrow{n}dS}_{\Delta(m\overrightarrow{V})_{12}}=\underbrace{-\int_{S_{1}}p_{1}\overrightarrow{n}-\int_{S_{2}}p_{2}\overrightarrow{n}\,dS}_{\overrightarrow{P_{f}}}+\overrightarrow{R_{w}}\]

Note

cette relation traduit le théorème fondamental de la dynamique pour un écoulement stationnaire:

la variation de la quantité de mouvement dans le volume fluide ( i.e la différence de flux entre l’entrée et la sortie $\Delta(m\overrightarrow{V})_{12}$ ) est égale à la somme des forces extérieures appliquées au volume fluide ( i.e. la force exercée par le fluide extérieur $\overrightarrow{P}_{f}$ et la force exercée par les parois $\overrightarrow{R_{w}}$)

Pour les quantités moyennes de la configuration étudiée, cela donne les 2 relations suivantes, qui donnent les 2 composantes des forces $R_x$ et $R_y$ exercées par les frontières solides (pression, viscosité) sur l’écoulement.

\[\begin{split}\begin{aligned} -\rho_{1}U_{1}^{2}S_{1} & = & p_{1}S_{1}+R_{x}\\ \rho_{2}U_{2}^{2}S_{2} & = & -p_{2}S_{2}+R_{y} \end{aligned}\end{split}\]

3.3.3. Bilan d’énergie#

Pour un écoulement stationnaire,

le flux d’enthalpie totale $h_t = h+\frac{1}{2}U^{2}+gz$ est égale à la puissance des forces extérieures $W_e$ et aux pertes $Q_v$ (par dissipation ou chaleur)

\[\int_{S}\rho(h+\frac{1}{2}U^{2}+gz)\overrightarrow{U}.\overrightarrow{n}\,dS = W_{e}+Q_{v}\]

Si on néglige les pertes, pour la configuration étudiée, on obtiens

\[\int_{S_{1}}\rho_{1}(h_{1}+\frac{1}{2}U_{1}^{2}+gz_{1})\overrightarrow{U_{1}}.\overrightarrow{n}\,dS+\int_{S_{2}}\rho_{2}(h_{2}+\frac{1}{2}U_{2}^{2}+gz_{2})\overrightarrow{U_{2}}.\overrightarrow{n}\,dS=0\]

qui traduit la conservation de l’énergie (entalpie totale par unité de masse) $e+\frac{p}{\rho}+\frac{1}{2}U^{2}+gz$ entre l’entrée et la sortie.

\[\rho_{1}(h_{1}+\frac{1}{2}U_{1}^{2}+gz_{1})U_{1}S_{1}=\rho_{2}(h_{2}+\frac{1}{2}U_{2}^{2}+gz_{2})U_{2}S_{2}\,\Longrightarrow u+\frac{p}{\rho}+\frac{1}{2}U^{2}+gz=cste\]

3.3.4. Théorème de Bernoulli#

Pour un écoulement stationnaire d’un fluide incompressible isotherme en négligeant les effets de viscosité, on applique ce bilan d’énergie sur un tube de courant: $h=e_{0}+p/\rho_{0}$, ce qui conduit à la conservation de l’énergie cinétique, le terme de pression et l’énergie potentielle (puisque l’énergie interne $e_0$ est constante).

Note

cette relation correspond au théorème de Bernoulli pour un fluide parfait incompressible

\[\frac{1}{2}V^{2}+\frac{p}{\rho_{0}}+gz=cste\]

Attention la cste dépend de la ligne de courant, sauf si le fluide est irrotationnel ( à partir du bilan de qté de mouvement).
On peut en déduire une approximation pour les quantités moyennes