5.3. Théorie de l’aile#
Marc BUFFAT département mécanique, Lyon 1
%matplotlib inline
import numpy as np
import sympy as sp
import matplotlib.pyplot as plt
from metakernel import register_ipython_magics
register_ipython_magics()
5.3.1. Théorie de la portance#
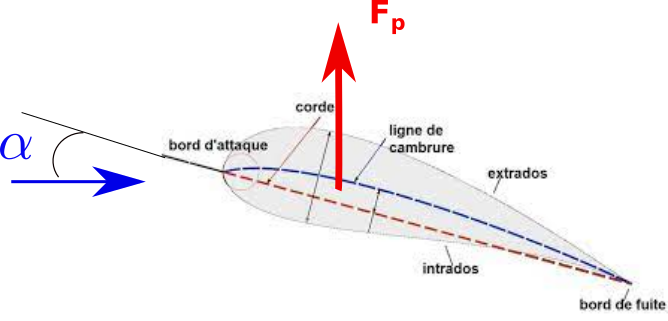
les différentes théories de la portance (sur internet):
Appuie de l’aile sur l’air (principe de réaction de Newton)
Bernoulli + égalité des temps de parcours
Analyse globale: bilan de quantité de mouvement, déviation de l’écoulement
Théorie de la Circulation de vitesse
lien vers le sondage sur https://l3-nbgrader/Survey/MGC3062L
#%activity /usr/local/commun/ACTIVITY/MGC3062L/portance
5.3.2. Caractéristique aérodynamique d’un profil#
Analyse dimensionnelle:
Etude d’un profil 2D
étude en fonction de l’angle \(\alpha\)
fonction du nombre de Reynolds
\(C_L\) coefficiant de portance: projection suivant \(\vec{N}=[-\sin\alpha, \cos\alpha]\) \(\perp\) à \(\vec{U}_0\)
\(C_m\) coefficient de moment (moment pression) par rapport à un point de référence \(P=[x_{ref}=0.25, y_{ref}=0]\) , qui n’est donc pas nécessairement sur la ligne moyenne à 1/4 de corde
on calcule alors le moment en un point Q quelconque par la relation de transport
d’où la position du centre de poussée exacte / à \(P\) \(x,y\) (erreur)
5.3.3. Analyse par bilan de quantité de mouvement#
Modèle simplifié des efforts exercés par un profil d’aile de longueur (de corde) \(L_c\) en incidence d’angle \(\alpha\) sur un écoulement stationnaire d’un fluide parfait incompressible de masse volumique \(\rho\) et de vitesse \(U_1\) (schéma ci-dessous)
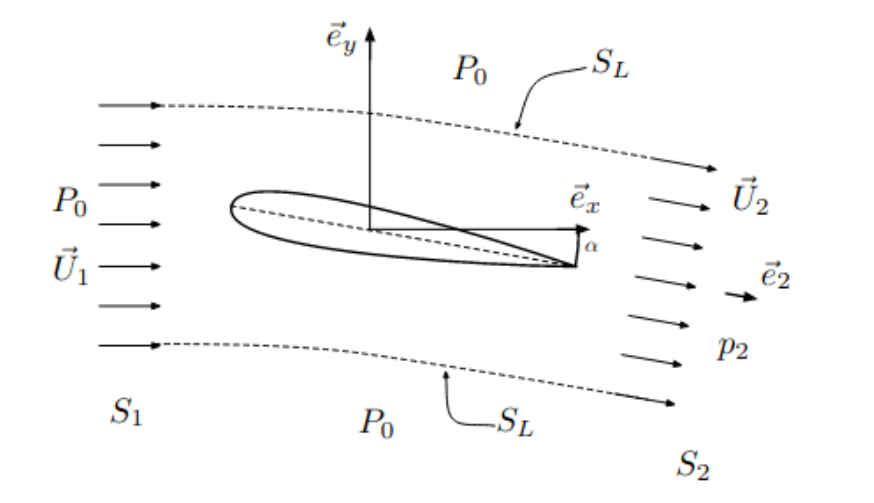
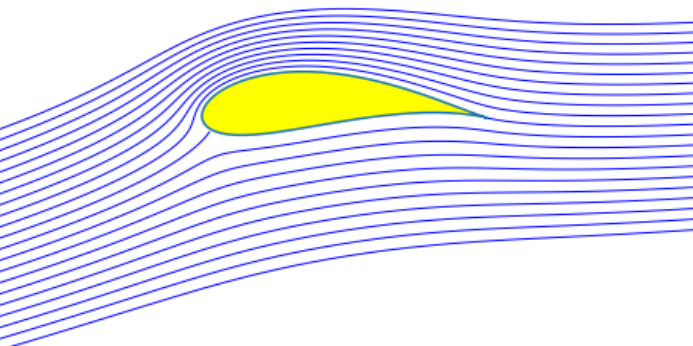
On constate expérimentalement que l’effet de l’aile sur l’écoulement, aux faibles incidences, est de dévier les lignes de courant d’un angle \(\alpha\) correspondant à l’angle d’incidence du profil, c.a.d l’angle d’inclinaison du bord de fuite.

d’après « How do wings work? » H. Babinsky, Physics Education 38(6) 2003
A 1-minute video released by the University of Cambridge sets the record straight on a much misunderstood concept - how wings lift. I start by giving the wrong explanation and asking who has heard it and every time 95% of the audience puts their hand up. Only a handful will know that it is wrong.Professor Holger BabinskyIt’s one of the most tenacious myths in physics and it frustrates aerodynamicists the world over. Now, …
from IPython.display import YouTubeVideo
YouTubeVideo('e0l31p6RIaY', width=600, height=400)
5.3.3.1. bilan de masse et de quantité de mouvement#
- \[ U_1 S_1 = U_2 S_2 \]
- \[ p_1 = p_2 = p_0 \]
- \[ S_2 = L_c W \]
on en déduit par bilan de quantité de mouvement la force de portance et le coefficient de portance \(C_p\)
soit à faible incidence une proportionnalité du coefficient de portance \(C_p\) avec l’angle d’incidence \(\alpha\)
5.3.4. Potentiel complexe#
Pour un écoulement incompressible 2D de fluide parfait irrotationnel le potentiel \(\phi(x,y)\) et la fonction de courant \(\psi(x,y)\) vérifie l’éuqtaion de Laplace:
dont le champ de vitesse \(\vec{U} = [U_x,U_y]\) en cartésien est donné par
On définit alors un potentiel complexe \(\Phi(z)\):
qui est une fonction analytique en z, dont la dérivée est indépendante de dz.
Dans ce cas \(\Phi(z)\) est différentiable en z et vérifie:
On le vérifie en prenant respectivement \(\delta z = \delta x \) et \(\delta z = i\delta y\) et en utilisant les relations de Cauchy-Riemann entre \(\phi\) et \(\psi\)
On en déduit le module de la vitesse:
et son angle \(\theta\)
5.3.4.1. Coordonnées polaires#
En coordonnées polaires, l’équation de Laplace s’écrit:
et le champ de vitesse en polaire
soit en coordonnées cartésiennes $\( U_x = U_r \cos\theta - U_\theta \sin \theta \mbox{ et } U_y = U_r \sin\theta + U_\theta \cos \theta\)$
5.3.4.2. Potentiel complexe en polaire#
puisque \(z = r e^{i\theta}\) on a donc :
avec $\( U_r = U_x \cos \theta + U_y \sin \theta \mbox{ et } U_\theta = -U_x \sin \theta + U_y \cos \theta\)$
On en déduit aussi
5.3.5. Potentiel complexe de l’écoulement autour d’un cylindre#
On a vu que l’écoulement potentiel autour d’un cylindre de rayon \(R\) en rotation est la somme d’un écoulement uniforme, d’un doublet et d’un vortex de circulation \(\Gamma\)
Pour une vitesse \(U_0\) d’incidence \(\alpha\) , le potentiel complexe s’écrit
et la vitesse complexe \(W = U- i V\)
# parametres
R, U0 = sp.symbols('R U_0',real=True, positive=True)
Gamma,alpha = sp.symbols('Gamma alpha',real=True)
# variables
theta,x,y = sp.symbols('theta x y',real=True)
r = sp.symbols('r',real=True,Positive=True)
# fonctions pour manipuler les complexes
from sympy import re,im,I
Pour une vitesse \(U_0\) d’incidence \(\alpha\) , le potentiel complexe s’écrit
# potentiel complexe Phi
z = sp.symbols('z')
Phi = U0*z*sp.exp(-I*alpha) + U0*sp.exp(I*alpha)*R**2/z \
- (I*Gamma/(2*sp.pi))*sp.log(z*sp.exp(-I*alpha)/R)
display("Phi(z)=",Phi)
'Phi(z)='
la vitesse complexe \(W = U- i V\) est alors donnée par $\( W = \frac{d \Phi}{d z}\)$
# calcul de la vitesse complexe W
W = 0
### BEGIN SOLUTION
W = sp.diff(Phi,z)
### END SOLUTION
display("W(z)=",W)
'W(z)='
# calcul fonction de courant psi (en fonction de (x,y)
psi = 0
### BEGIN SOLUTION
psi = im(Phi.subs(z,x+sp.I*y))
### END SOLUTION
display('psi(x,y)=',psi)
'psi(x,y)='
# en déduire les composantes de vitesse dans Ux et Uy
Ux = 0
Uy = 0
### BEGIN SOLUTION
Ux = re(W.subs(z,x+sp.I*y))
Uy = -im(W.subs(z,x+sp.I*y))
### END SOLUTION
display("Ux=",Ux)
display("Uy=",Uy)
'Ux='
'Uy='
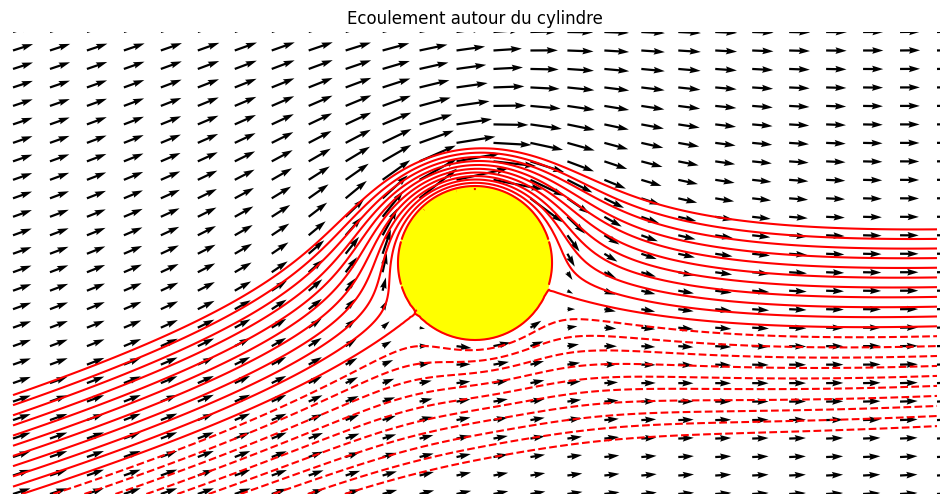
5.3.5.1. Visualisation des champs#
utilisation d’une technique de masque pour éliminer l’écoulement à l’intérieur du cercle
# parametres numeriques: choix arbitraire de Gamma et alpha !
R0 = 0.5
Uinf = 1.0
vals = [(Gamma,-2*np.pi*R*U0),(alpha,np.deg2rad(10)),(R,R0),(U0,Uinf)]
display("parametres:",vals)
'parametres:'
[(Gamma, -6.28318530717959*R*U_0),
(alpha, 0.17453292519943295),
(R, 0.5),
(U_0, 1.0)]
# domaine de calcul et maillage (grille) pour le calcul de psi et de la vitesse
L = 3
N = 201
pas = 8 # pas pour les vitesses
# points de calcul
xg = np.linspace(-L,L,N)
yg = np.linspace(-L/2,L/2,N)
# pour les lignes de courant psi
X, Y = np.meshgrid(xg, yg)
# utilisation d'un masque
Z = X + 1j*Y
Z = np.ma.masked_where(np.absolute(Z)<0.95*R0,Z)
X = Z.real
Y = Z.imag
# et le champ de vitesse U
XX = X[::pas,::pas]
YY = Y[::pas,::pas]
# calcul des valeurs numeriques
psi1 = sp.lambdify([x,y],psi.subs(vals),'numpy')
u1 = sp.lambdify([x,y],Ux.subs(vals),'numpy')
v1 = sp.lambdify([x,y],Uy.subs(vals),'numpy')
with np.errstate(divide='ignore'):
Psi1 = psi1(X,Y)
Psi0 = psi1(0.5,0)
Levs = np.linspace(Psi0-L/5,Psi0+L/5,21)
U1 = u1(XX,YY)
V1 = v1(XX,YY)
<lambdifygenerated-1>:2: RuntimeWarning: invalid value encountered in sqrt
return -0.17364817766693*x + 0.984807753012208*y + 1.5707963267949*log(2.0*sqrt(x**2 + y**2))/pi + 0.25*imag(exp(0.174532925199433*1j)/(x + 1j*y))
# tracer
fig, ax = plt.subplots(figsize=(12,6))
#ax.contourf(X,Y,Psi1,levels=21)
ax.contour(X,Y, Psi1,levels=Levs,colors='r')
ax.quiver(XX,YY,U1,V1)
cercle = plt.Circle((0.,0.),R0,color='yellow')
ax.add_artist(cercle)
plt.axis('equal')
plt.axis('off')
plt.title("Ecoulement autour du cylindre");
5.3.6. Transformation conforme#
On définit une transformation conforme \(Z=F(z)\) qui préserve les angles dans le plan complexe.
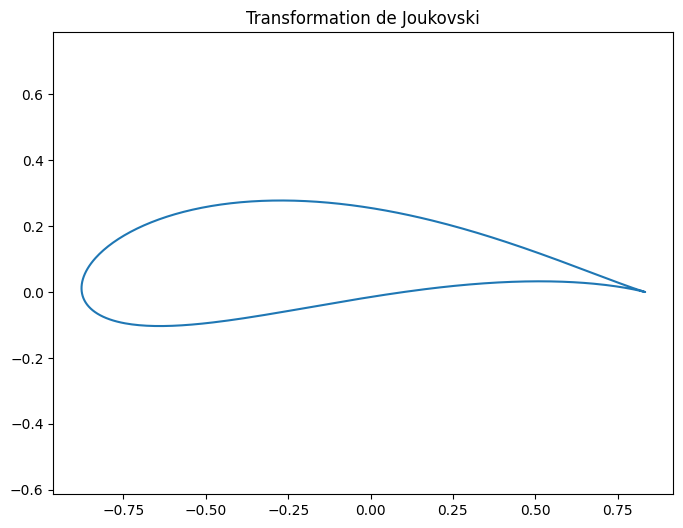
5.3.6.1. Transformation de Joukovski#
avec \( z = x + i y \) (plan d’origine) et \(Z = X + i Y\) (plan transformé)
C = sp.symbols('C',real=True,positive=True)
F = lambda z: z + C**2/z
display("Z=F(z)",F(z))
'Z=F(z)'
5.3.6.2. transformation conforme#
transformation de l’écoulement autour d’un cercle de centre \(x0,y0\) de rayon \(R=R_0\)
\(c\) paramétre de la transformation \(0\le c\le 1\)
\(\beta\) angle du point centre / horizontal
# selection cas 1,2,3,4 (choix 4 par defaut)
cas = 4
beta = 0
if cas==0:
# cercle
x0 = 0
y0 = 0
R0 = float(R.subs(vals))
c = float(R.subs(vals)*0.0)
elif cas==1:
# parametres pour une ellipse
x0 = 0
y0 = 0
R0 = float(R.subs(vals))
c = float(R.subs(vals)*0.9)
elif cas==2:
# parametre pour une plaque
x0 = 0
y0 = 0
R0 = float(R.subs(vals))
c = float(R.subs(vals)*1.0)
elif cas==3:
# parametres pour un profil symetrique
R0 = float(R.subs(vals))
c = float(R.subs(vals)/1.2)
x0 = c - R0
y0 = 0
else:
# parametres pour un profil cambre
beta = np.deg2rad(8)
R0 = float(R.subs(vals))
c = float(R.subs(vals)/1.2)
x0 = c - R0*np.cos(beta)
y0 = R0*np.sin(beta)
# calcul de la transformation en coordonnées cartésienne
xc = re(F(x+sp.I*y))
yc = im(F(x+sp.I*y))
display("xc,yc=",xc,yc)
'xc,yc='
# transformation du cercle
Xc = sp.lambdify([x,y],xc.subs(C,c),'numpy')
Yc = sp.lambdify([x,y],yc.subs(C,c),'numpy')
Theta = np.linspace(0,2*np.pi,410)
XC = Xc(x0+R0*np.cos(Theta),y0+R0*np.sin(Theta))
YC = Yc(x0+R0*np.cos(Theta),y0+R0*np.sin(Theta))
plt.figure(figsize=(8,6))
plt.plot(XC,YC)
plt.title("Transformation de Joukovski")
plt.axis('equal');
5.3.6.3. calcul de l’écoulement par transformation de Joukovski#
calcul pour un profil
transformation numérique
def TransJ(Z,lam):
'''transformation Joukovski (complexe)'''
return Z + lam**2/Z
def Cercle(C0,R):
'''pts du cercle de centre C0 (complexe) et de rayon R'''
Theta = np.linspace(0,2*np.pi,200)
return C0 + R*np.exp(1j*Theta)
def solutionJ(PHI,lam,C0,R,xg,yg):
'''calcul de la solution par transformation de Joukovski PHI'''
X,Y = np.meshgrid(xg,yg)
Z = X+1j*Y
Z = np.ma.masked_where(np.absolute(Z-C0)<=R,Z)
Zc = Z - C0
#Phiz = PHI(Z)
# BUG numpy: calcul
# np.log(Z) cannot be calculated correctly due to a numpy bug np.log(MaskedArray);
Phiz = Zc.copy()
with np.errstate(divide='ignore'):
for m in range(Zc.shape[0]):
for n in range(Zc.shape[1]):
Phiz[m,n] = PHI(Zc[m,n])
# Joukovski transformation
J = TransJ(Z, lam)
cercle = Cercle(C0, R)
airfoil= TransJ(cercle, lam)
return J, Phiz.imag, airfoil
#valeur des parametres
display("parametres ",vals)
alpha0 = np.rad2deg(float(alpha.subs(vals)))
print("alpha={} deg. beta={} deg. c={} C0={}".format(alpha0,np.rad2deg(beta),c,x0+1j*y0))
'parametres '
[(Gamma, -6.28318530717959*R*U_0),
(alpha, 0.17453292519943295),
(R, 0.5),
(U_0, 1.0)]
alpha=10.0 deg. beta=8.0 deg. c=0.4166666666666667 C0=(-0.0784673677041185+0.06958655048003272j)
display(Phi)
# calcul du potentiel complexe
PhiJ = Phi.subs(vals)
display("Phi(z)=",PhiJ)
# conversion fonction python
PHI = sp.lambdify(z,PhiJ)
'Phi(z)='
# calcul solution ! pble mauvaise valeur de la circulation
J, Psi, airfoil = solutionJ(PHI,c,x0+1j*y0,R0,xg,yg)
# tracer
fig=plt.figure(figsize=(12,8))
ax=fig.add_subplot(111)
# this means that the flow is evaluated at Juc(z) since c_flow(Z)=C_flow(csi(Z))
cp=ax.contour(J.real, J.imag, Psi,levels=Levs, colors='blue', linewidths=1,
linestyles='solid')
ax.plot(airfoil.real, airfoil.imag)
ax.fill(airfoil.real, airfoil.imag,color='yellow')
plt.axis('off')
plt.title("Problème: eclt au bord de fuite car circulation non correcte")
ax.set_aspect('equal');
#plt.savefig('eclt_cylindre.png')
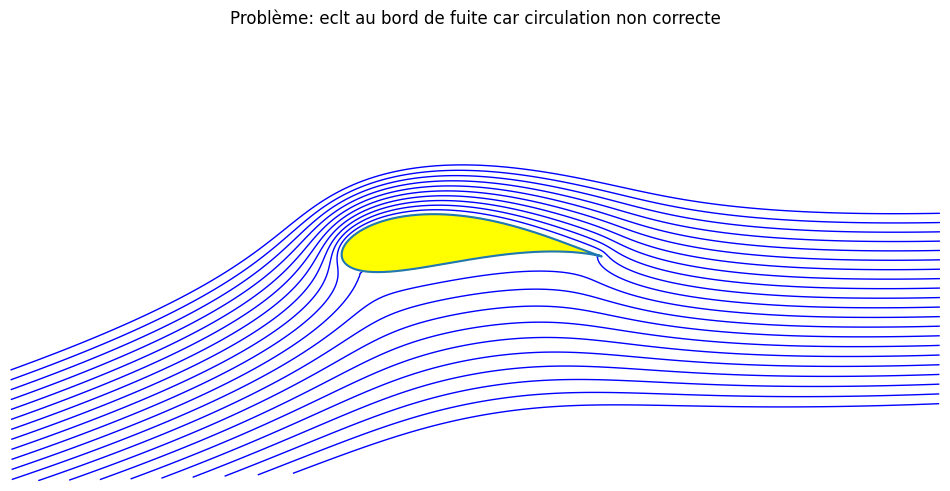
5.3.6.4. circulation de Kutta-Joukovsky#
condition de Kutta au bord de fuite !
# valeur de Joukovski
GammaJ = -4*sp.pi*U0*R*sp.sin(alpha+beta)
display("GammaJ=",GammaJ)
# potentiel Joukovsky
PhiJ = Phi.subs(Gamma,GammaJ).subs(vals)
display("PhiJ=",PhiJ)
# conversion fonction python
PHI = sp.lambdify(z,PhiJ)
'GammaJ='
'PhiJ='
# calcul solution
J, Psi, airfoil = solutionJ(PHI,c,x0+1j*y0,R0,xg,yg)
# tracer
fig=plt.figure(figsize=(12,8))
ax=fig.add_subplot(111)
# this means that the flow is evaluated at Juc(z) since c_flow(Z)=C_flow(csi(Z))
cp=ax.contour(J.real, J.imag, Psi,levels=Levs, colors='blue', linewidths=1,
linestyles='solid')
ax.plot(airfoil.real, airfoil.imag)
ax.fill(airfoil.real, airfoil.imag,color='yellow')
plt.axis('off')
ax.set_aspect('equal');
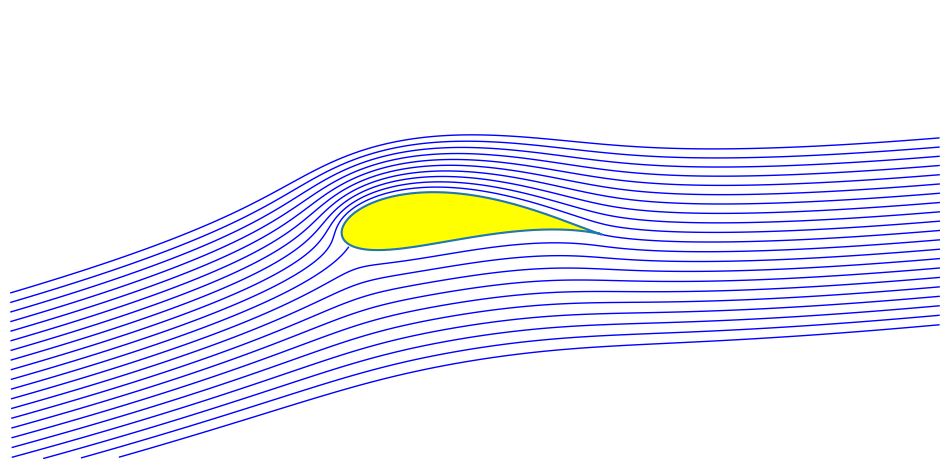
5.3.7. Calcul de la Portance#

5.3.7.1. Condition de Kutta - Joukovsky#
création circulation vitesse \(\Gamma\) telle que la vitesse reste parallèle au bord de fuite (pas de contournement)
condition de kutta-joukovski
circulation
portance
en faible incidence
5.3.7.2. Expérience de Prandtl (~1918)#
création de la circulation

from IPython.display import YouTubeVideo
YouTubeVideo('VcggiVSf5F8', width=600, height=400)
5.3.8. Annexe: Joukovski-airfoil#
Ce notebook est inspiré d’un notebook de calcul de l’écoulement autour d’un profil de Joukovski
